基于改进遗传算法的舰船物资转运方案研究＊

王 凯 赵彦森

（海军驻郑州地区军事代表室 郑州 450015）

1 引言

现代大中型水面舰船在执行作战任务以及进行海上补给的时候，需要在甲板和贮存舱室之间转运大量的武器弹药、零部件和生活物品等物资。为了满足作战需求并避免诸如弹药等具有较高危险性的物资长时间暴露于甲板，需要安全高效地进行物资转运［1～3］。因此，如何通过采用先进的技术手段和措施，获得最优的物资转运方案，对于提高转运效率和载舰安全性具有重要的意义。

本文建立了舰船物资转运方案决策模型，并采用遗传算法对模型进行了求解运算，有效解决了车辆配置和转运路径的优化问题。

2 模型建立

2.1 问题描述

舰船物资通常由专用的转运车进行转运，其转运可简单描述为：假设在一次物资转运任务中要将物资由中转站转运到n个贮存舱室，有m辆转运车可供使用，要运往每个贮存舱室的物资量为wi（i＝1，2，…，n），每辆转运车的最大装载量为q，要合理安排车辆和转运路径，以使总路径最短。

2.2 模型建立

令物资中转站编号为0，各贮存舱室的编号为1，2，…，n，转运车辆的编号为1，2，…，k，每个路径（i，j）对应的长度为lij，将该问题简化为最短路径问题，则目标函数为

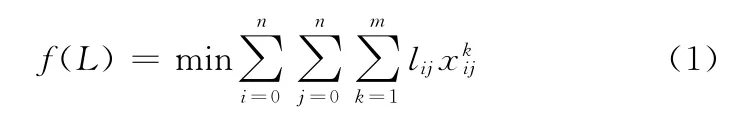
并满足以下约束条件：

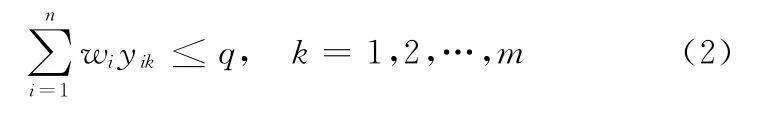
其中：

式（2）表示在转运过程中转运车辆的载货量不能超过其最大装载量。

3 遗传算法设计

3.1 编码方案

由于遗传算法不能直接处理解空间数据，因此必须将问题编码，转换成遗传空间的基因型串结构数据［4～5］。编码的好坏直接影响选择、交叉、变异等遗传运算，是设计遗传算法的关键和应用难点之一。在这里，针对要解决的车辆配置和转运路径优化问题，采用自然数编码方法。图1为染色体结构图，C1～Cn表示贮存舱室，其值为贮存舱室编号，长度由贮存舱室的数量决定。V1～Vm表示车辆分配，其值为该车辆所要保障的贮存舱室个数，长度由需要的车辆数决定。需要说明的是，实际上只有染色体的前半部分参与遗传运算。

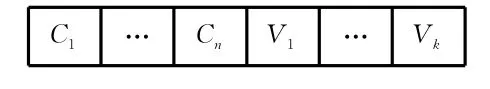
图1 染色体结构图

如染色体［3 1 4 2 5∣2 3］表示用两辆车从中转站前往五个储存舱室运送物资，第一辆车负责两个贮存舱室的物资转运，第二辆车负责三个贮存舱室的物资转运，车辆分配和转运方案为：

第一辆车：从物资中转站出发，依次运送物资到3号贮存舱室和1号贮存舱室，返回中转站。

第二辆车：从物资中转站出发，依次运送物资到4号贮存舱室、2号贮存舱室和1号贮存舱室，返回中转站。

3.2 种群的初始化

设定种群规模N，步骤如下：

1）对n个舱室随机进行排序，得到染色体前n位C1～Cn；

2）按步骤1得到染色体的前n位从左到右进行计算，若前i个舱室要转运的物资量小于或等于车辆的载重量q，并且前（i＋1）个舱室要转运的物资量大于车辆的载重量q，则令染色体的V1为i，即该辆车负责前i个舱室的物资转运；

3）从染色体的第（i＋1）位开始，按照步骤2对剩下的（n－i）个舱室从左到右进行计算，得到V2。如此反复，直到所有的舱室都被安排完毕，得到一个染色体。

4）重复前三步，直到得到N个染色体。

3.3 适应度函数

适应度函数是根据目标函数确定的用于区分群体中个体好坏的标准，是遗传算法设计的一个重要方面，如果设计不当，可能造成某个局部最优解，影响算法的全局优化性能。针对本文要解决的问题，设计适应度函数如下：

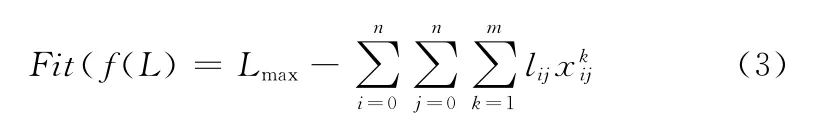
式中Lmax为一个适当的相对比较大的数。

3.4 选择算子

选择算子对群体中的个体根据适应度值大小进行优胜劣汰操作，适应度高的个体被遗传到下一代群体中的概率较大。本文选用随机遍历抽样，该算法使用N个相等距离的指针从随机排列的种群中来选择个体，每个个体被选择的概率为

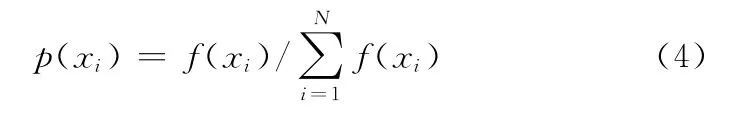
3.5 交叉算子

交叉运算产生的新个体具有父代的一部分遗传物质，交叉算子的设计和实现与具体问题密切相关，并要和编码设计一同考虑。由于本文采用自然数编码方式，进行交叉运算会产生大量不可行解，因此这里不进行交叉运算。

3.6 变异算子

变异操作模仿生物遗传和进化过程中的基因突变现象，将个体染色体编码串中的某些基因座上的基因值用其他等位基因来替换，从而形成一个新的个体。变异算子能够改善遗传算法的局部搜索能力，维持群体的多样性，防止出现早熟现象。遗传算法中通常的变异算子不适用于本文的车辆配置和转运路径优化问题，这里构造了一种特殊的变异算子，即设定变异概率后，对每个要变异的个体随机确定两个基因位，将其基因值进行互换。

3.7 进化终止条件

当进化达到最大进化代数或连续几代的适应度值没有明显变化时，则停止进化得到最优解。

4 算法验证

为验证本文所提算法的有效性，运用Matlab语言编程实现该算法，并针对国内外常用的测试实例进行仿真计算。

4.1 小规模测试实例

为了便于比较，对参考文献［8～12］都采用的实例进行计算。设定初始种群为60，最大进化代数为50，随机进行20次计算，平均值为67.85，获得最优解67.5的百分率为80%，对应的车辆分配和转运方案为：［4 7 6 2 8 5 3 1∣3 5］。几种算法结果对比见表1，可以看出本文算法的计算结果要优于文献［7，9～10］的结果，图2为经过50次迭代后最优解的变化和种群均值的变化曲线。

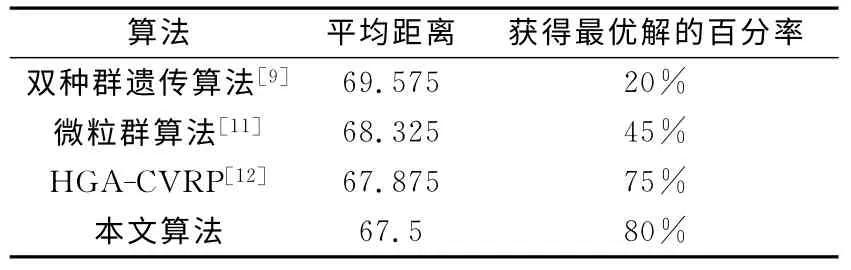
表1 几种算法20次计算结果的统计表

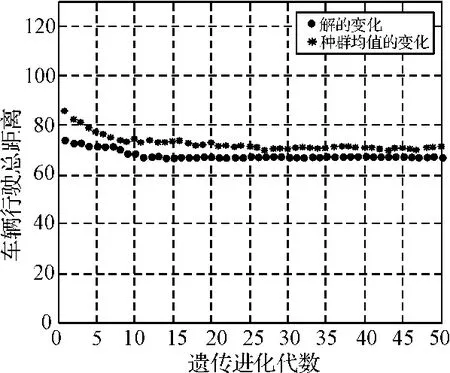
图2 初始种群60迭代次数50

4.2 中等规模测试实例

为了验证本文算法对于更大规模测试实例的有效性，从网址http：／／branchandcut.org／下载测试实例E－n22－k4进行计算。为了与文献［12］进行对比分析，设定初始种群为60，最大进化代数为50，随机进行10次运算，计算结果见表2，可见本文算法结果明显优于文献［12］。图3为经过50次迭代后最优解的变化和种群均值的变化曲线，获得局部最优解为431，对应的车辆分配和转运方案为：［19 21 20 17 10 2 1 6 8 11 13 16 18 15 12 14 3 4 7 5 9∣4 7 5 5］。

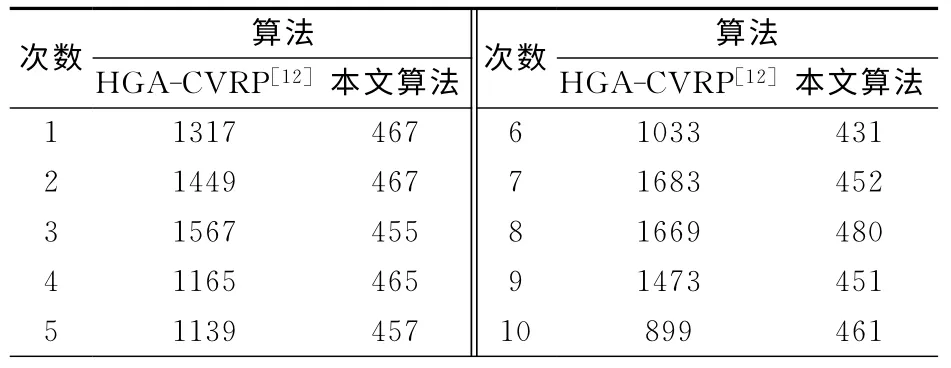
表2 初始种群60迭代次数50计算结果

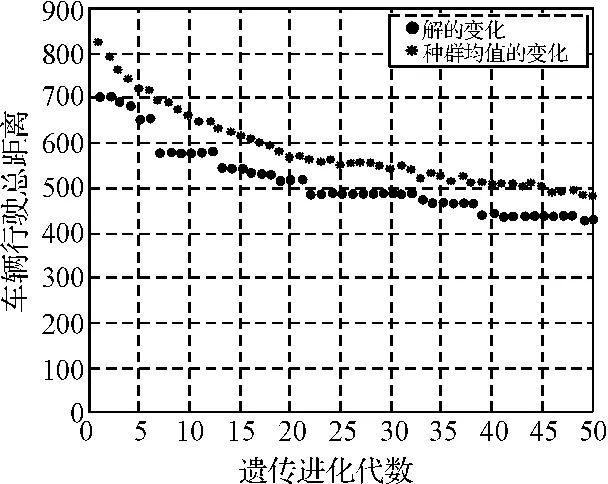
图3 初始种群60迭代次数50

图4为初始种群为200时经过100次迭代后最优解的变化和种群均值的变化曲线，获得最优解为375，而文献［12］在初始种群为200时要经过1000次迭代才能得到最优解。

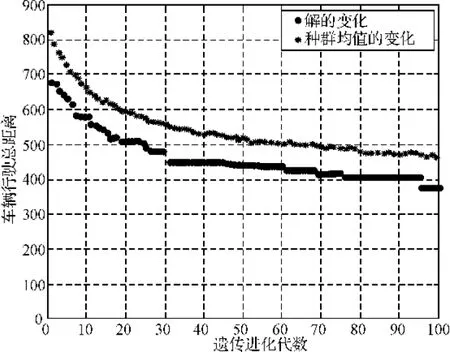
图4 初始种群200迭代次数100

5 结语

本文建立的转运方案决策模型和设计的遗传算法能够有效解决车辆配置和转运路径优化问题，可以为舰船物资转运提供最优方案，具有一定的实用性。

［1］张晓东，童剑，郭敏，等.舰船物资转运方案计算机辅助决策算法研究［J］.中国舰船研究，2011，6（4）：104－110.

［2］马登武，郭小威，吕晓峰.基于改进遗传算法的舰载机弹药调度［J］.工程与应用，2010，9：1－7.

［3］陈希林，季新源，粟嘉立.航空弹药挂载方案优化模型及其遗传算法求解［J］.系统仿真学报，2009，21（16）：5175－5178.

［4］李敏强，寇纪淞，林丹，等.遗传算法的基本理论与应用［M］.北京：科学出版社，2003：1－28.

［5］雷英杰，张善文，李续武，等.Matlab 遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005：45－61.

［6］冯蓉，杨建华.基于改进遗传算法的动态交通分配优化研究［J］.计算机与数字工程，2012（6）.

［7］张立斌，高仲春.基于遗传算法的数据挖掘维度选择［J］.计算机与数字工程，2012（5）.

［8］张丽萍，柴跃廷.车辆路径问题的改进遗传算法［J］.系统工程理论与实践，2002，22（8）：79－84.

［9］赵燕伟，吴斌，蒋丽，等.车辆路径问题的双种群遗传算法求解方法［J］.计算机集成制造系统，2004，10（3）：303－306.

［10］张涛，张玥杰，王梦光.不确定车辆数的车辆路径问题模型和混合算法［J］.系统工程理论方法应用，2002，6（5）：21－24.

［11］肖健梅，李军军，王锡淮.求解车辆路径问题的改进微粒群优化算法［J］.计算机集成制造系统，2005，11（4）：577－581.

［12］姜昌华.遗传算法在物流系统优化中的应用研究［D］.上海：华东师范大学，2007：61－80.