关于几个最值问题的研究

●李建潮 (双林中学 浙江湖州 313012)

1 相关问题

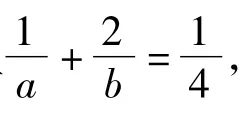
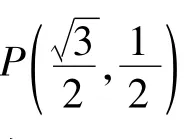
易知：问题2与问题3是同一个问题(由同一作者提供)，这是一个很经典的问题;问题1与问题2(即问题3)如出一辙、一脉相承，本文与读者一起探究如下.

2 问题之见

美国著名数学家哈尔莫斯有言：“问题是数学的心脏”.杨之先生对问题解答的要求是“解决一个数学问题应是严谨的、简练的和初等的”.对此我们深表赞同，对于经典问题的解答不但在于解决问题之本身，而且更在于“问题之外”之扩张;不仅是思想和方法的展示，更是思想和方法的雕塑和再创造;与美接轨，还应力求(而并非强求)解答的艺术性，集数学的学术、艺术与“魔术”于一体，使整个解答惟妙惟肖、似诗如画.

3 问题新解

下面拟用纯粹的代数方法，并巧施待定系数法构造柯西模型来展示3个相关问题的初等解法.先来解问题1：

解令正数α，β满足α2+β2=1，则由二元柯西不等式

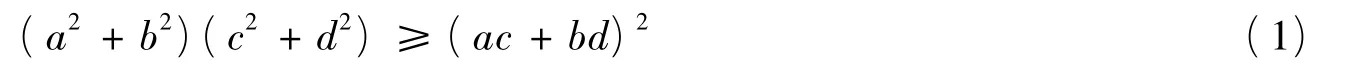
(a，b，c，d∈R，当且仅当 bc=ad 时等号成立)，得

用上述方法，可获得以下一般情形：

再处理问题2(即问题3)，笔者直接处理下面的一般情形：

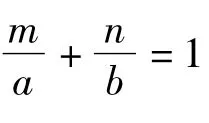
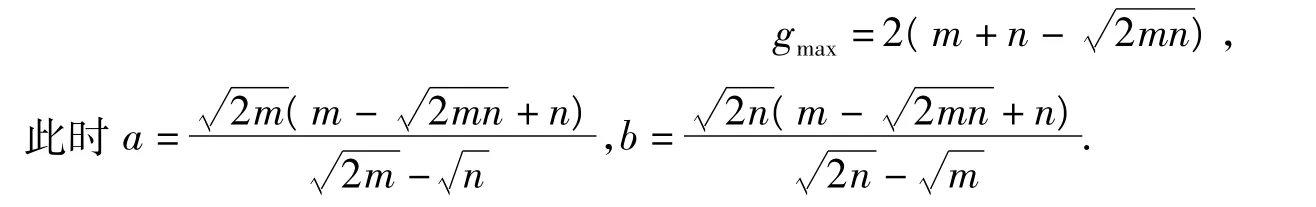
证明令正数α，β满足α2+β2=1，则由二元柯西不等式(1)，得

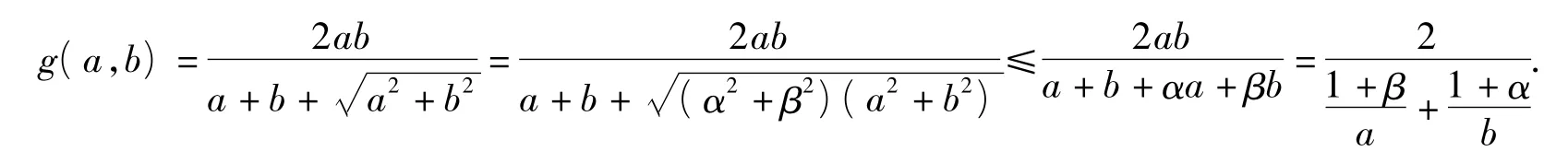
4 一脉相承

细心的读者不难发现：问题1的求解与定理2的证明不尽协调，前者连续2次应用了二元柯西不等式，而后者只用了1次;如果用求解问题1的方法来证明定理1，似乎很难完成证明.这种顾忌不无道理，其实，我们可以借定理2的证明之东风对问题1的求解方法进行再雕塑，从而使定理1与定理2的证明方法接轨.

下面展示定理1的这一创造性证明方法：

证明令正数 α，β满足 α2+β2=1，则

特别地，当

令1-β=km，1-α=kn(其中 k为正数)，则

由此可见，不论是从内容看还是从证明方法看，定理1与定理2如出一辙、一脉相承(文首的3个问题只是它们的特例而已).

［1］ 侯典峰.问题征解3［J］.数学通讯：上半月，2010(1/2)：131.

［2］ 王勇.问题征解2［J］.数学通讯：上半月，2010(1/2)：131.

［3］ 王勇.2010 年3 月1845 号问题［J］.数学通报，2010(3)：66.