“完美无缺”的解答 扑朔迷离的错误
●朱良满 (溆浦县第一中学 湖南溆浦 419300)
常言道:人非圣贤,孰能无过;知错就改,善莫大焉!在解题过程中,不出错永远是一种理想状态.教师和学生的解题能力在与错误、失败的不屈斗争中得到了提高.实际解题中,由于认知能力的欠缺和思维的局限性,一些问题的解答,我们认为“完美无缺”,其实漏洞百出;还有一些问题,我们明知解答有“错”,但不知“错”在何处,为何而“错”.知道错了是好事,而对错误的深层次反思,更是在积累着宝贵的知识财富.
笔者在教学过程中发现,很多学生自认为解答“完美无缺”,而当教师指出错误后,学生仍很难发现错在何处,因何而错.
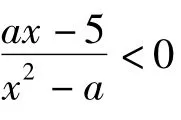

由题意知,a满足条件
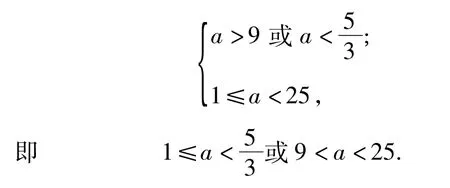
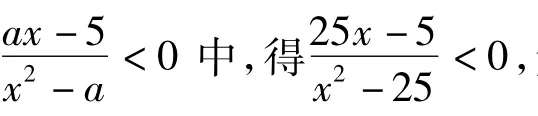
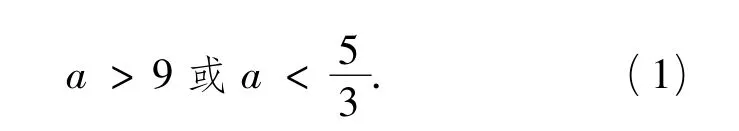
由式(1)和式(2)知,a满足
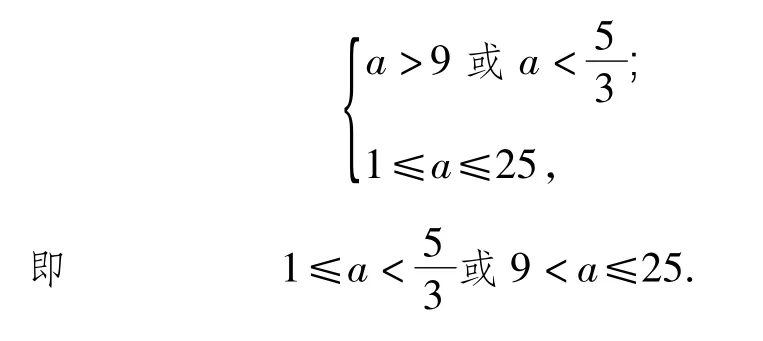
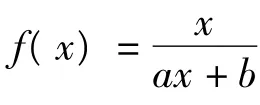
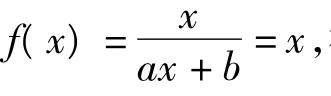

要使方程(3)有唯一解,则
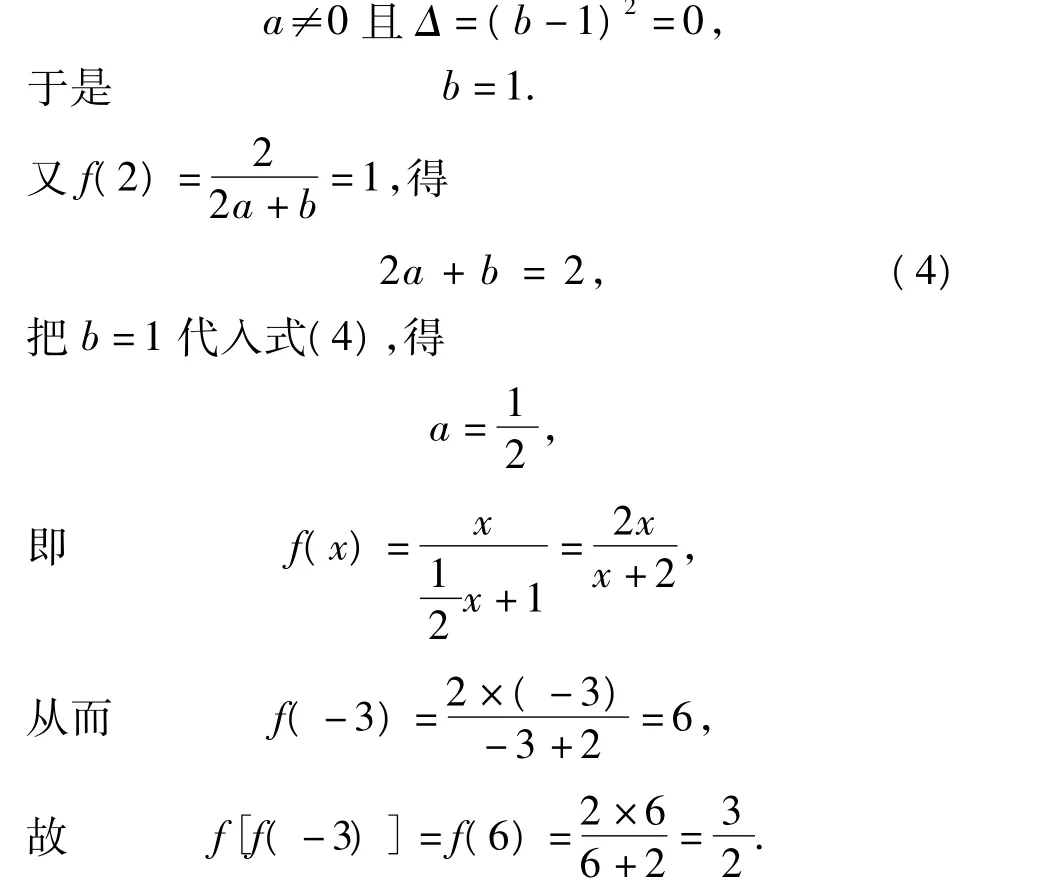
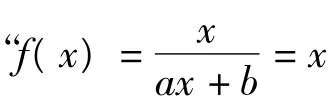
正解 由上述解答过程知,ax2+bx=x有唯一解,得

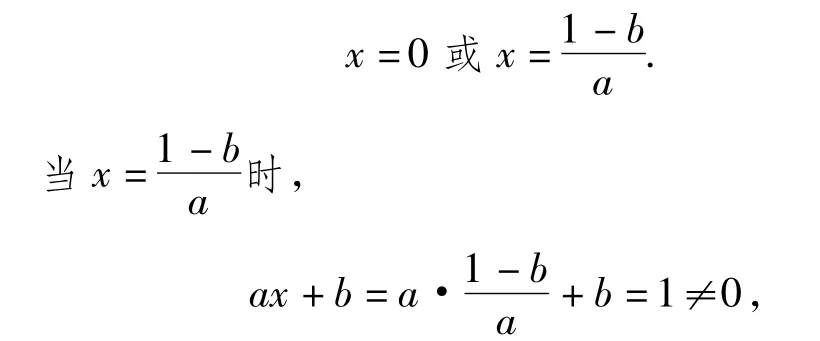

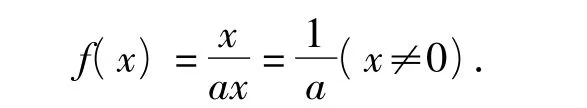
由 f(2)=1知a=1,即 f(x)=1(x≠0).
例3 已知 0<α<β<γ<2π,且 cosα+cosβ+cosγ =0,sinα +sinβ +sinγ =0,求 β - α 的值.
错解由已知得

将上述2个式子两边平方,再相加,得
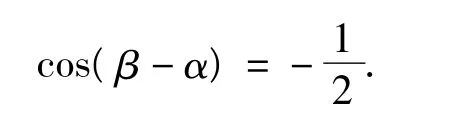
又由0<α<β<γ<2π,知0<β-α<2π,因此
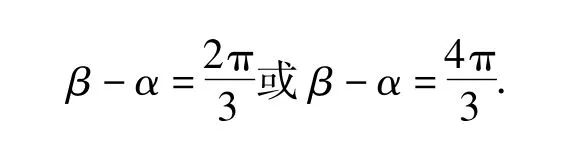
分析由 cosβ +cosγ =-cosα,sinβ +sinγ =-sinα两边平方,相加,得
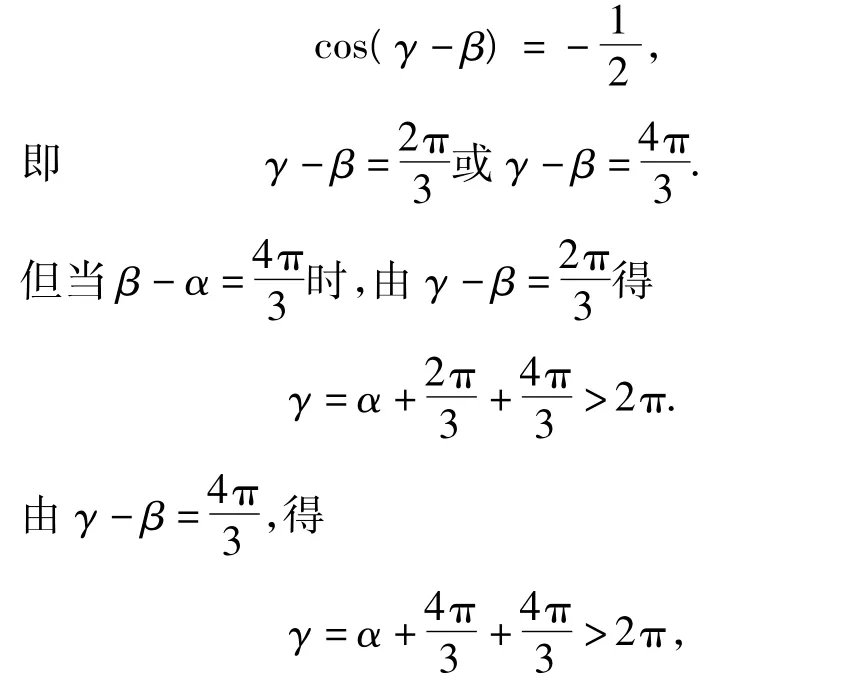
本题为什么容易出现错解的情况呢?原来,将cosα +cosβ =-cosγ,sinα +sinβ =-sinγ 两边平方,再相加,得
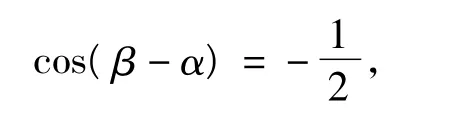
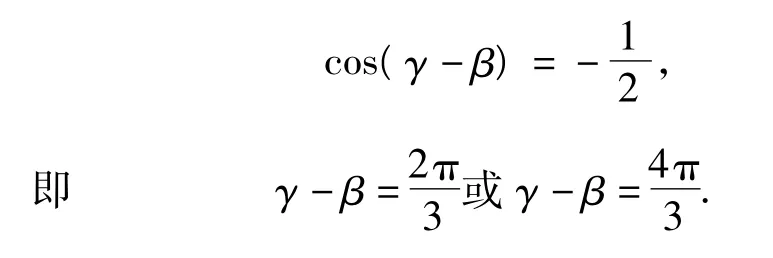
将 cosα +cosγ =-cosβ,sinα +sinγ =-sinβ 平方,相加,得

综上所述,由0<α<β<γ<2π,知
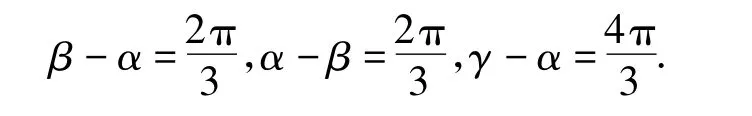

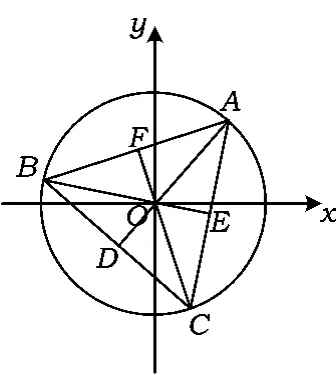
图1
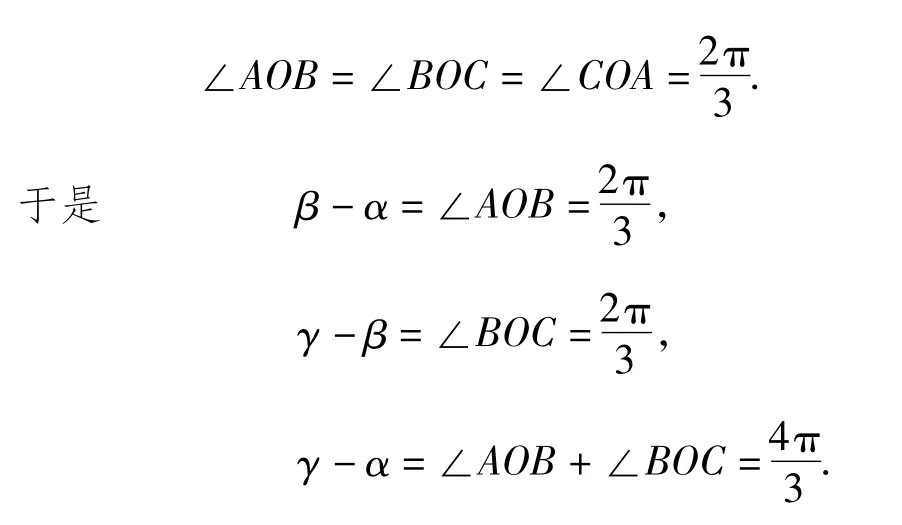
在“完美无缺”的解答中,种种扑朔迷离的错误,其实隐藏着思考的盲区,如例1和例2中的“分母不能为0”,在实际解题中总是被忽视.我们所犯的“漏解”、“多解”等种种错误,即原命题被我们随意地缩小、扩大了条件所应满足的范围.错误的产生不是坏事,它能促使师生共同反思,以发现错误的根源,而其最有效的标尺,就是在解题的过程中,始终坚持等价转化的思想.
——溆浦鹅

