一个不等式的另证及推广
2013-08-27 03:39邹生书阳新县高级中学湖北阳新435200
中学教研(数学) 2013年1期
●邹生书 (阳新县高级中学 湖北阳新 435200)
《数学通报》2010年第12期宋庆老师提供的第1 885号数学问题如下:
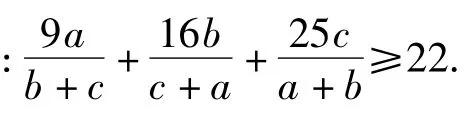
文献[1]、文献[2]和文献[3]对该不等式给出了证明和推广.本文给出了一种新的证明,并通过柯西不等式和判别式法给出不等式的几种推广.
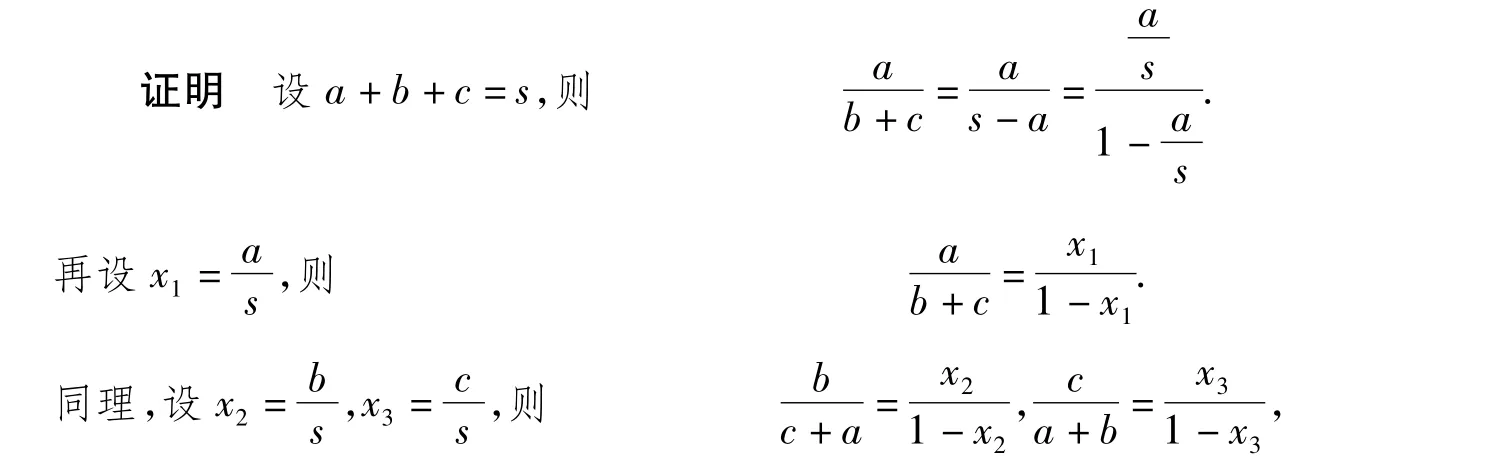
且x1+x2+x3=1.故原问题可转化为:
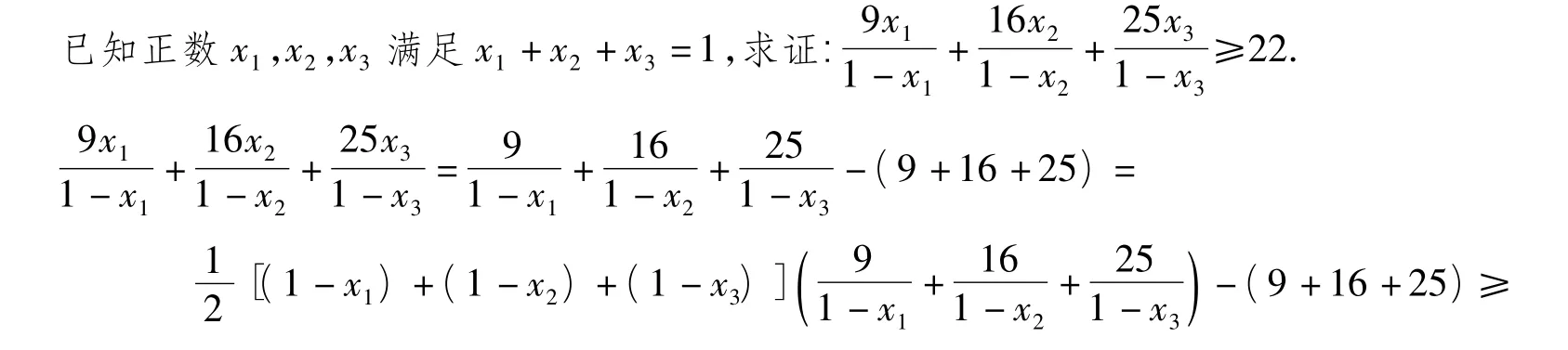
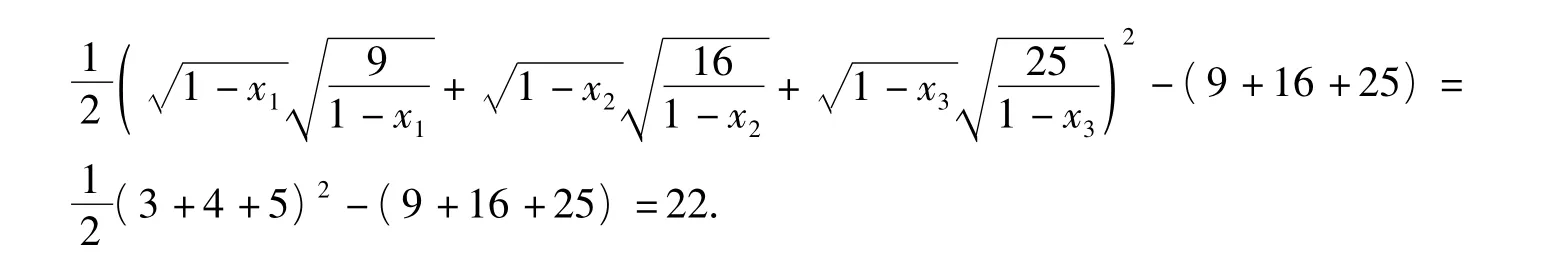
推广1 已知 a,b,c为正数,且 p,q,r为正常数,求证:
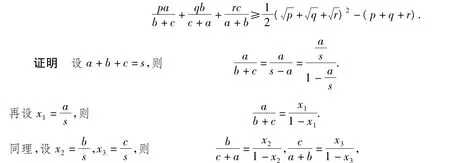
且x1+x2+x3=1.故原问题可转化为:
已知正数 x1,x2,x3满足 x1+x2+x3=1,求证:
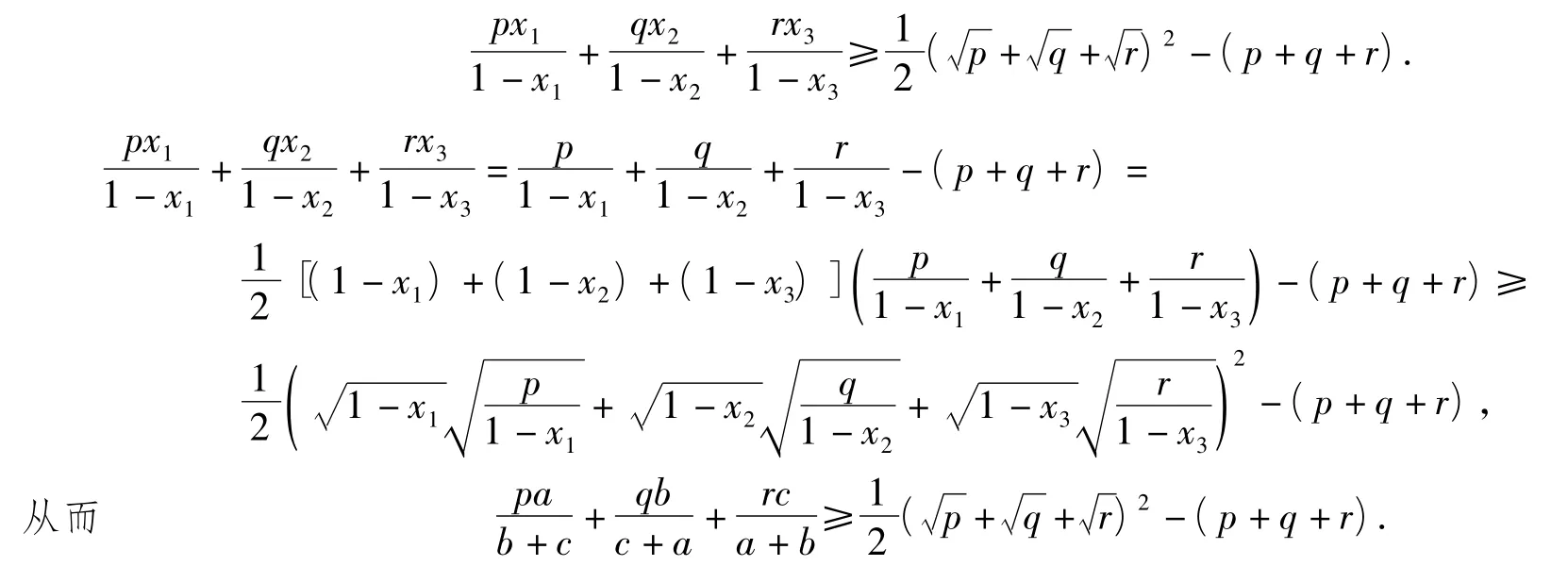
推广 2 已知 a1,a2,…,an为正数,且 m1,m2,…,mn为正常数,n≥3,则

推广3 已知变量a,b,c为正数,且λ,μ为正常数,求证:恒成立.

当k=48时,由式(1)得b≤c恒成立,这与题设不符,故式(1)恒成立当且仅当
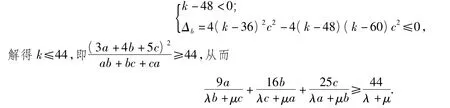
推广4 已知变量a,b,c为正数,且p,q,r为正常数,求证:
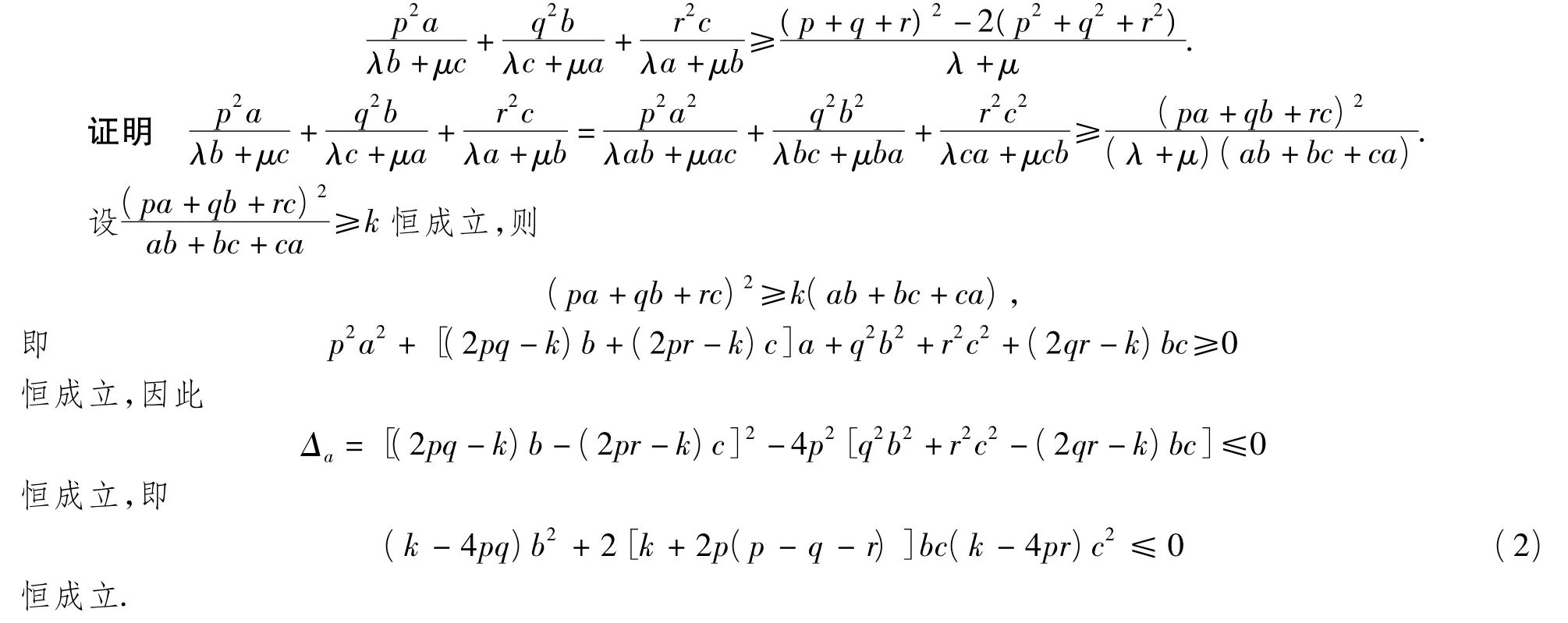
当k=4pq时,由式(2)得(q-p-r)b+(q-r)c≤0,但当 q-p-r>0时此式不成立,因此 k≠4pq,故式(2)恒成立,则当且仅当k-4pq<0且
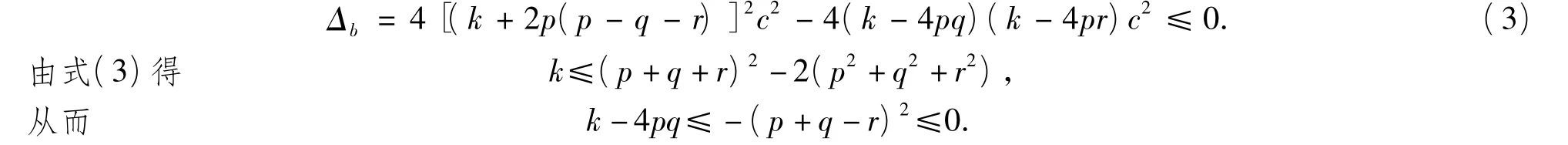
又k≠4pq,所以k-4pq<0.故式(2)恒成立的充要条件是
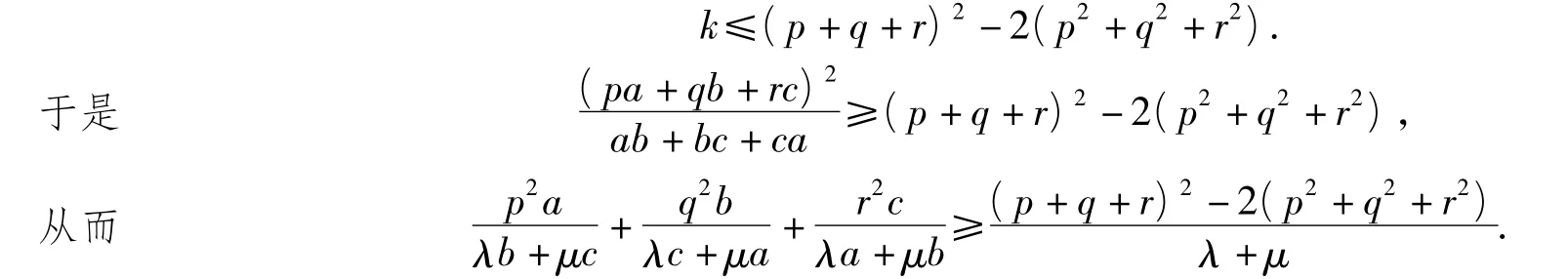
根据推广4笔者进一步提出如下更一般的猜想.
猜想已知变量ai和常数pi,λi(i∈N,i≥3)均为正数,则
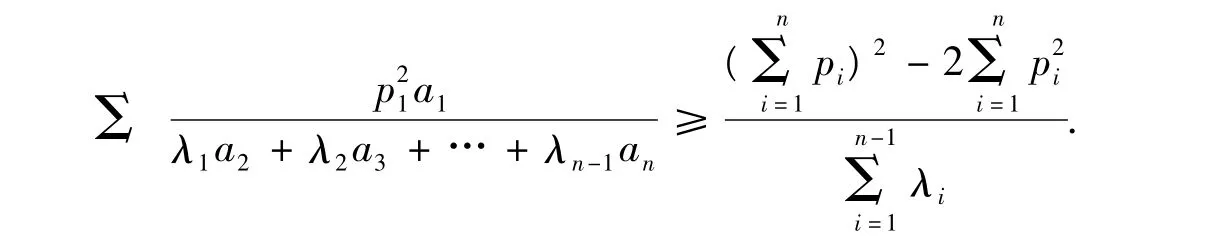
[1] 宋庆.数学问题解答[J].数学通报,2010(12):59-61.
[2] 钟建新.数学问题1 885的解后再思考[J].数学通报,2012(3):50-51.
[3] 宋志敏,尹枥.数学问题1 885的推广与再研究[J],数学通报,2011(12):27-28.
猜你喜欢
轻工标准与质量(2022年4期)2022-08-25
轻工标准与质量(2022年3期)2022-06-29
轻工标准与质量(2022年1期)2022-03-07
轻工标准与质量(2021年6期)2021-12-31
中等数学(2020年7期)2020-11-26
中学生数理化·七年级数学人教版(2019年9期)2019-11-25
中学生数理化·中考版(2018年9期)2018-11-09
中学生数理化·七年级数学人教版(2016年8期)2016-12-07
中学生数理化·中考版(2016年8期)2016-12-07
读写算·高年级(2009年8期)2009-08-12

