区域图形的对称性

●李世杰 (衢州市教育局教研室 浙江衢州 324002)●李 盛 (衢州市第一中学 浙江衢州 324000)

定义 由D：f(x，y)≥0(或 ＞，＜，≤，=之一)约束的点集称为平面区域，简称区域.其图形称为区域图形.

这样定义的区域由方程或不等式刻划.区域可以退化为曲线、直线或点等.区域可以看作是二维的点的轨迹.

作为曲线关于点或直线可能存在的对称性的推广，下面探讨平面区域可能存在的关于点或直线的对称性质.

定理1 (区域图形对称定理)设区域D：f(x，y)≥0(或＞，＜，≤，=之一).

(1)若 f(-x，y)=f(x，y)，则区域 D 关于 y轴(x=0)对称;

(2)若 f(x，-y)=f(x，y)，则区域 D 关于 x轴(y=0)对称;

(3)若 f(-x，-y)=f(x，y)，则区域 D 关于原点(0，0)对称;

(4)若 f(x，y)=f(y，x)，则区域 D 关于直线y=x对称;

(5)若 f(x，y)=f(-y，-x)，则区域 D 关于直线y=-x对称.

证明不妨设区域D：f(x，y)≥0.

(1)设(x0，y0)是区域D上的任意一点，那么f(x0，y0)≥0，于是

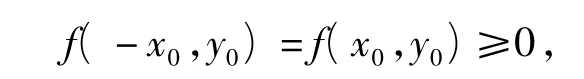
说明(-x0，y0)也在区域 D 上，而(x0，y0)，(-x0，y0)关于y轴对称，即区域D关于y轴对称.

类似可证后面4个结论.

注区域轴对称有以下结论：

(1)若同时有

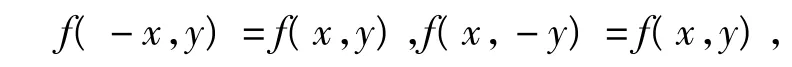
则区域f(x，y)≥0关于x轴、y轴都对称.

(2)特殊区域f(|x|，y)≥0关于x轴对称;区域 f(x，|y|)≥0关于 y轴对称;区域 f(|x|，|y|)≥0关于x轴、y轴、原点都对称.

(3)顺时针旋转θ角，由得转轴公式由注(2)，利用转轴公式，得到

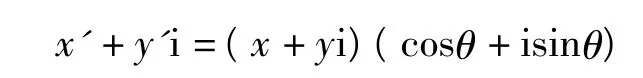
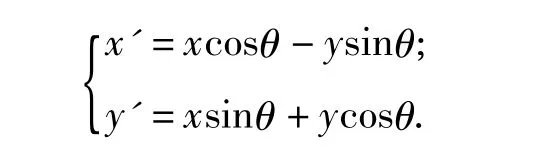
区域 f(|xcosθ-ysinθ|，xsinθ+ycosθ)≥0 关于 xsinθ+ycosθ=0对称;

区域 f(xcosθ-ysinθ，|xsinθ+ycosθ|)≥0 关于 xcosθ-ysinθ=0对称;

区域 f(|xcosθ-ysinθ|，|xsinθ+ycosθ|)≥0关于直线 xsinθ+ycosθ=0和直线 xcosθ-ysinθ=0及原点都对称.

同时具有定理1中5条对称性质的图形是存在的，如：

例1 试绘出|x|+|y|≤2之区域图形.

解以-x代x，-y代y，所给不等式不变，则不等式|x|+|y|≤2的区域图形关于x轴、y轴都对称.因此，可先讨论x≥0，y≥0的情形.

当x≥0，y≥0时，所给不等式可化为x+y≤2，所围区域图形为△MON闭区域.

根据对称性，关于x，y轴作它的对称图形，获得所给不等式|x|+|y|≤2的整个区域图形(包括边界)为正方形MNKL闭区域(如图1).

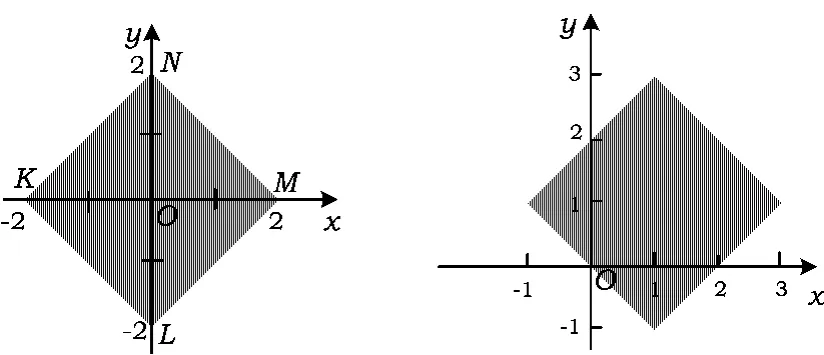
图1 图2

注对于|x-1|+|y-1|≤2之区域图形，令x'=x-1，y'=y-1，得|x'|+|y'|≤2，其区域图形为中心在原点、边长为2的正方形.通过平移，知所给不等式的图形为中心在(1，1)、4个顶点为(1，3)，(3，1)，(1，-1)，(-1，1)的正方形闭区域(如图2).

例2 试求方程|x-1|+|x+1|+|y-1|+|y+1|=4的区域图形面积.

解以-x代x，-y代y，所给方程不变，故方程|x-1|+|x+1|+|y-1|+|y+1|=4的区域图形关于x轴、y轴都对称.因此，可先讨论x≥0，y≥0的情形.

当x≥0，y≥0时，所给方程化为

其解为 0≤x≤1，0≤y≤1，区域图形是以 O(0，0)，A(1，0)，B(0，1)，E(1，1)为顶点的正方形闭区域(如图3)，面积为1平方单位，故所给方程的区域图形面积为4平方单位.

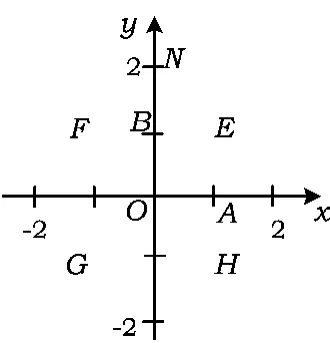
图3

例3 试绘出(|x|-1)2+(|y|-1)2=1和(|x|-1)2+(|y|-1)2≤1的区域图形.

解类似例1和例2，可绘出(|x|-1)2+(|y|-1)2=1和(|x|-1)2+(|y|-1)2≤1的区域(如图4，图5).

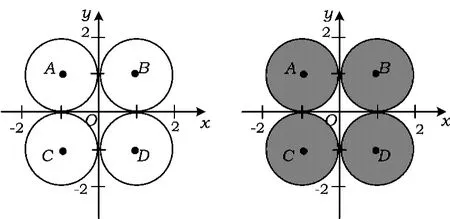
图4 图5

例4 试绘出|x+y|+|x-y|≤2的区域图形.

解因为互换 x，y或互换-x，y，所给不等式皆相同，故其区域图形直线 y=x，y=-x对称.

我们只要讨论x+y≥0，xy≥0的情形.此时，所给不等式化为

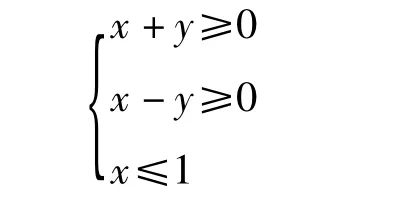
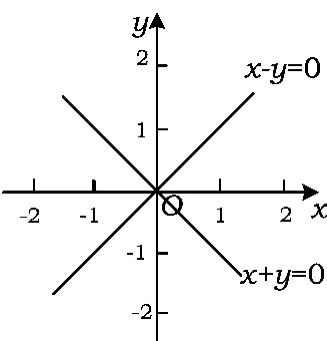
图6

这样，由不等式组所表示的图形是以(0，0)，(1，1)，(1，-1)为顶点的三角形闭区域(如图6).

将此三角形区域关于直线y=x，y=-x连续3次作对称变换，即可得到所给不等式的整个区域图形：以x-y=0，x+y=0为对角线(也是对称轴)的正方形(边长为2，中心为(0，0)).

例5 试绘出||x|-1|+||y|-1|≤2之区域图形.

解因为分别用-x，-y代 x，y，所给不等式皆相同，故其区域图形应对称于直线x=0，y=0.令 x≥0，y≥0，只要讨论|x-1|+|y-1|≤2，由例1后的注，知其图形为一个五边形，5个顶点为(0，0)，(2，0)，(3，1)，(1，3)，(0，2).

画出其在第一象限的区域图形(以点(1，1)为中心的正方形闭区域)，然后根据对称性，关于x，y轴作它的对称图形，获得所给不等式||x|-1|+||y|-1|≤2的整个区域图形(包括边界)：粗体“十”字(如图7).

类似地，我们可绘出不等式-2|x|-2|y|+3|x-y|+3|x+y|≤2围成的四角星形区域图形(如图8).

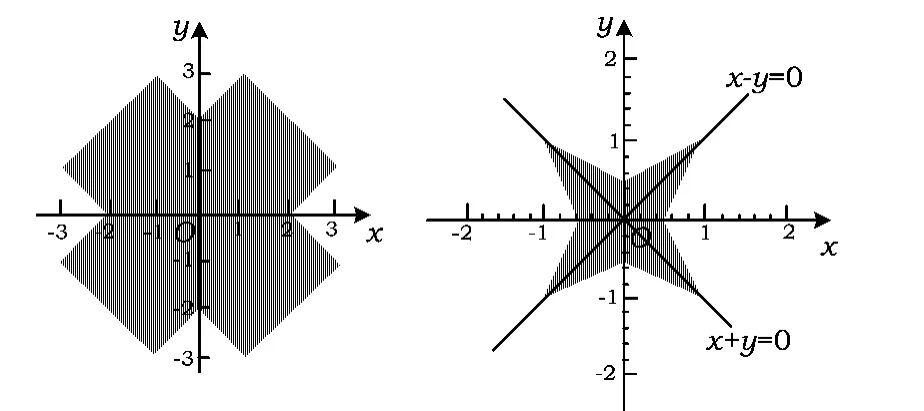
图7 图8

这是中心为(0，0)的四角星形区域.

例1～例5中区域图形，均同时具有定理1中5条对称性质.实际上，这样的区域一定具有旋转不变性，即图形旋转45°仍然与原图形重合.

定理2 区域 f(x，y)≥0(或 ＞，＜，≤，=之一)关于点P(a，b)的对称区域为不等式f(2a-x，2b-y)≥0(或相应的＞，＜，≤，=之一).

证明略.

特殊情况：区域f(x，y)≥0关于原点的对称区域为不等式f(-x，-y)≥0.

例6 试绘出|x+y-1|+|x-y-2|≤2关于点(1，1)的对称区域图形.

解根据定理2，只需在所给不等式中以(2-x，2-y)替换(x，y)，即得对称区域的不等式为

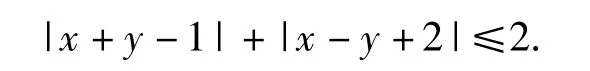
在此不等式中，不论x+y-1，x-y+2为正或负，所给的不等式皆相同，也就是说图形应对称于直线x+y-1=0和直线x-y+2=0.这样，我们只须讨论x+y-1≥0，x-y+2≥0即可.此时所给的不等式可化为

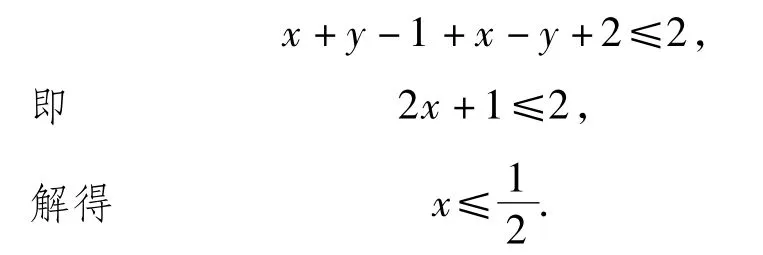
于是，所给不等式的区域图形由不等式组

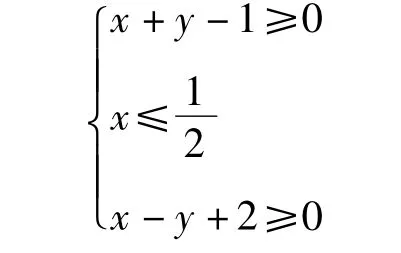
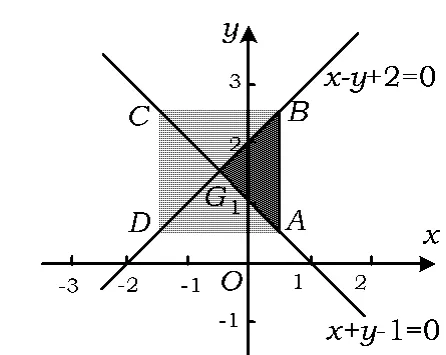
图9

约束，它表示△ABG闭区域(如图9).

例7 试绘出不等式|x-2|+||x-2|-2y|≤2关于点(1，0)的对称区域图形.

解根据定理2，只需在所给不等式中以(2-x，-y)替换(x，y)，即得对称区域的不等式为

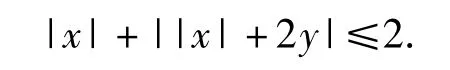
在此不等式中，以-x代x，y不变，所给不等式没有变化，从而不等式|x|+||x|+2y|≤2的区域图形关于y轴对称.因此，也可先讨论x≥0的情形，再用对称法，绘出整个区域图形.

当x≥0时，所给不等式化为

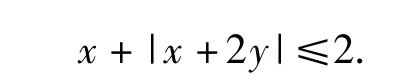
(1)若 x+2y≥0，则 x+y≤1，不等式组

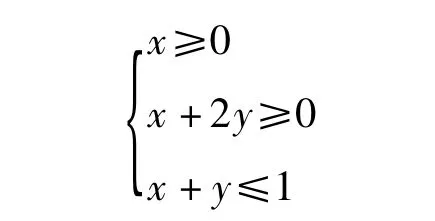
表示的区域图形是以 A(0，1)，C(2，-1)，O(0，0)为顶点的三角形闭区域(含边界)(如图10).

(2)若 x+2y＜0，则 y≥-1，不等式组

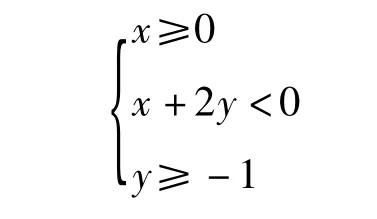
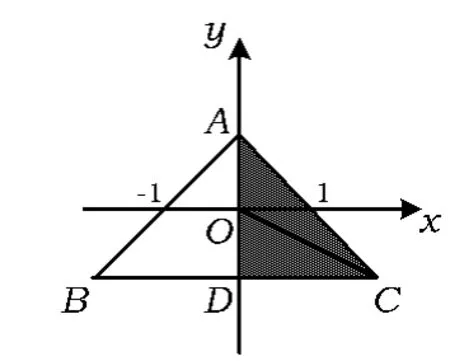
图10

表示的区域图形是以 D(0，

-1)，C(2，-1)，O(0，0)为顶点的三角形闭区域(含边界)(如图10).

由于所给不等式的区域图形关于y轴对称，故不等式的区域图形是以 A(0，1)，B(-2，-1)，C(2，-1)为顶点的三角形闭区域(含边界).

定理3 区域 f(x，y)≥0(或 ＞，＜，≤，=之一)关于直线Ax+By+C=0(A，B不同时为0)的对称区域为不等式

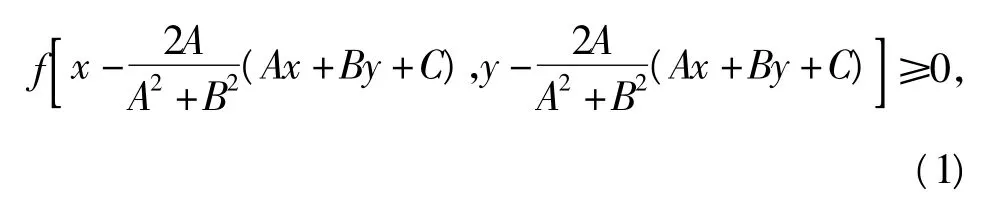
(或相应的＞，＜，≤，=之一).

证明设f(x，y)≥0上任一点P0(x0，y0)关于直线Ax+By+C=0的对称点为P(x，y)，则

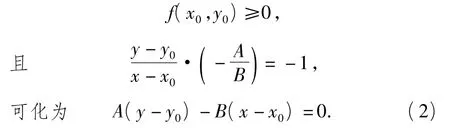
注意到当B=0时，式(2)成立，又由P0P的中点在直线Ax+By+C=0上，得

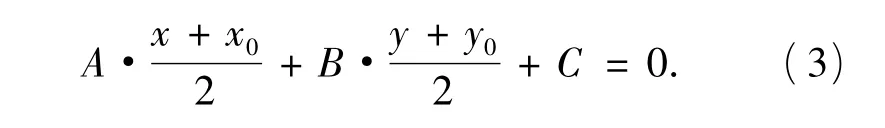
由式(2)，式(3)解得

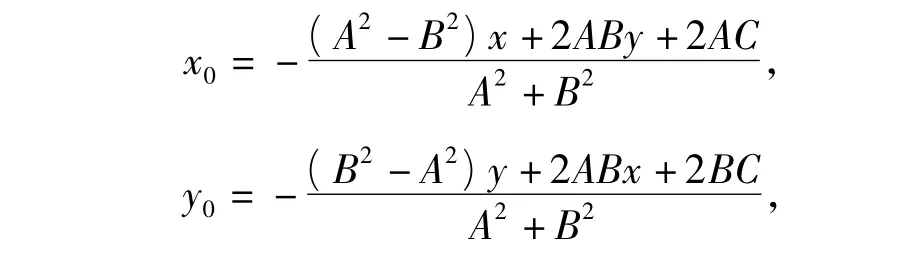
化成易记形式

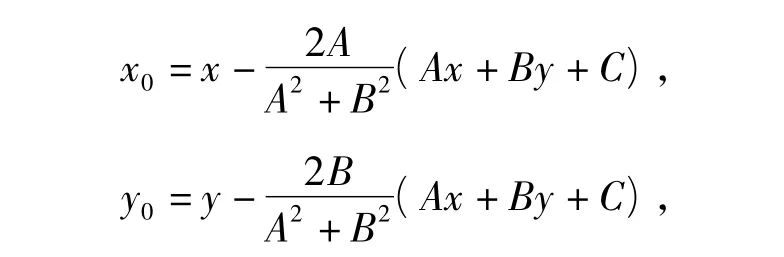
代入 f(x0，y0)≥0，得点 P(x，y)在区域(1)上.

反过来，可证得：区域(1)上任一点关于直线Ax+By+C=0的对称点，也在区域f(x，y)≥0上.

作为定理3的特殊情况，有：

(1)区域f(x，y)≥0关于x轴的对称区域为不等式 f(x，-y)≥0;

(2)区域f(x，y)≥0关于y轴的对称区域为不等式 f(-x，y)≥0;

(3)区域f(x，y)≥0关于直线x=a的对称区域为不等式f(2a-x，y)≥0;

(4)区域f(x，y)≥0关于直线y=b的对称区域为不等式f(x，2b-y)≥0;

(5)区域f(x，y)≥0关于直线x+y+c=0的对称区域为不等式f(-y-c，-x-c)≥0;

(特例：f(x，y)≥0 与 f(-y，-x)≥0 的区域图形关于直线y=-x对称.)

(6)区域f(x，y)≥0关于直线x-y+c=0的对称区域为不等式f(y-c，x+c)≥0.

(特例：f(x，y)≥0与 f(y，x)≥0的区域图形关于直线y=x对称.)

观察其本质，只需对原不等式中x，y的位置用相应的式子代即可，如关于直线x=a对称，当且仅当2a-x代替 x，y不变;关于点 P(a，b)对称，则用2a-x代 x，2b-y代 y等等.

例8 试绘出不等式2|y|+||y|+3x|≤6关于直线y=x的对称区域图形.

解根据定理3，互换所给不等式中 x，y的位置，得关于直线 y=x的对称区域不等式为

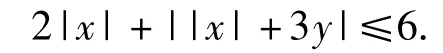
以-x代 x，y不变，所给不等式没有变化，从而不等式2|x|+||x|+3y|≤6的区域图形关于y轴对称.因此，也可先讨论x≥0的情形，再用对称法，绘出整个区域图形.

当x≥0时，所给不等式化为

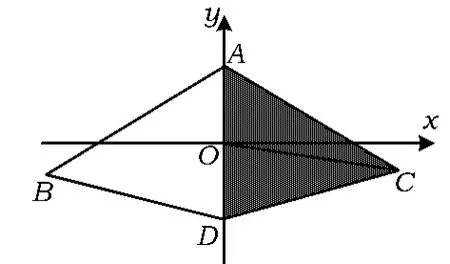
图11

(1)若 x+3y≥0，则 x+y≤2，不等式组

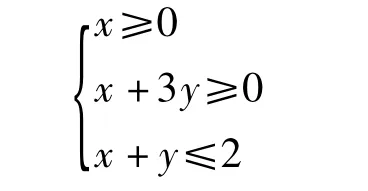
所表示的区域图形是以 A(0，2)，C(3，-1)，O(0，0)为顶点的三角形闭区域(含边界).

(2)若 x+3y＜0，则 x-3y≤6，不等式组

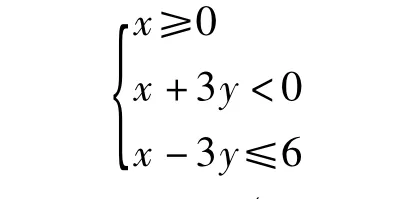
所表示的区域图形是以 D(0，-2)，C(3，-1)，O(0，0)为顶点的三角形闭区域(含边界)(如图11).

由于所给不等式的区域图形关于y轴对称，故不等式的区域图形是以 A(0，2)，B(-3，-1)，C(3，-1)，D(0，-2)为顶点的凸四边形闭区域(含边界)(如图11).

例9 试绘出不等式|y-1|+|2|y-1|+1-x|≤3的关于直线y=1-x的对称区域图形.

解根据定理3，在所给不等式中作替换(1-y，1-x)→(x，y)，得关于直线 y=1-x 的对称区域不等式为

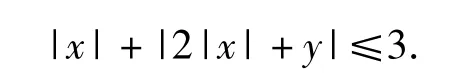
以-x代x，y不变，所给不等式没有变化，从而不等式|x|+|2|x|+y|≤3的区域图形关于y轴对称.因此，也可先讨论x≥0的情形，再用对称法，绘出整个区域图形.

当x≥0时，所给不等式化为

x+|2x+y|≤3.

(1)若 2x+y≥0，则 3x+y≤3，不等式组

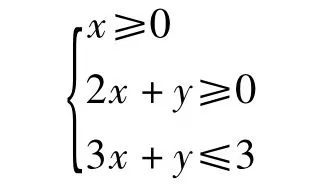
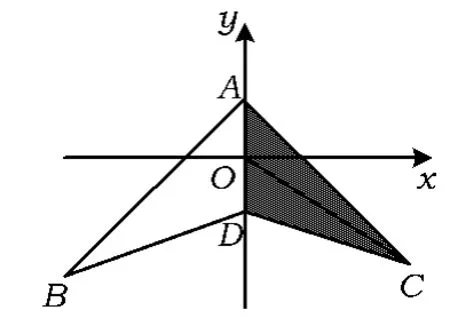
图12

所表示的区域图形是以 A(0，3)，C(3，-6)，O(0，0)为顶点的三角形面.

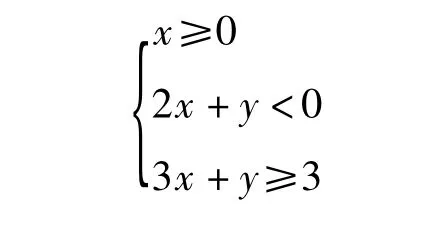
(2)若2x+y＜0，则 x+y≥3，不等式组所表示的区域图形是以 D(0，-3)，C(3，-6)，O(0，0)为顶点的三角形面.

由于所给不等式的区域图形关于y轴对称，故不等式的区域图形是以 A(0，3)，B(-3，-6)，C(3，-6)，D(0，-3)为顶点的凹四边形面(如图12).

例10 试绘出不等式|7x-24y+30|-|24x+7y-40|≤25关于直线3x+4y-5=0的对称区域图形.

解根据定理3，关于直线3x+4y-5=0的对称变换为

即在所给不等式中作替换

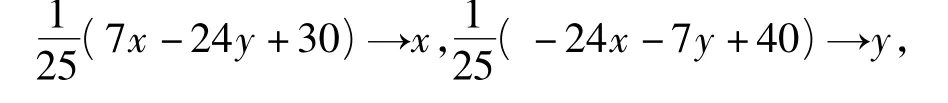
得关于直线3x+4y-5=0的对称区域不等式为

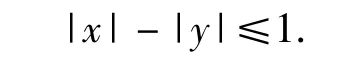
以-x代x，-y代 y，所给不等式不变，故不等式|x|-|y|≤1的区域图形关于x轴、y轴都对称.因此，可先讨论 x≥0，y≥0的情形，再用对称法，绘出整个区域图形.

当x≥0，y≥0时，所给不等式化为x-y≤1，其区域图形如图13所示，再根据区域图形关于x轴、y轴都对称，绘出整个区域图形：双折线内区域.

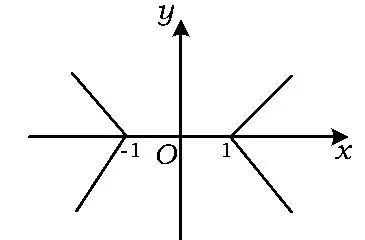
图13

［1］ 李世杰，李盛.函数不等式［M］.杭州：浙江大学出版社，2009.

［2］ 李世杰，李盛.函数元不等式的理论及其应用［M］.杭州：浙江大学出版社，2011.