基于Vissim的3相交通流理论应用＊

荆彬彬 林培群 徐建闽

（华南理工大学土木与交通学院 广州510640）

0 引 言

交通流理论在20世纪30年开始发展，一开始以数学和物理学方法来建模交通流理论。数理统计中的泊松分布、二项分布等被用来描述交通流的到达规律，随后相继出现了跟驰理论、波动理论和排队理论等［1］。从20世纪90年代起，交通流理论有了新的发展。Nagel和Schreckenberg在1992提出了元胞自动机（cellular automaton）模型，而Kerner和Rehborn在1996年在驶入匝道附近发现了一种特殊的现象，从自由流到阻塞流的滞后的相变，他们称之为“同步流”，韩国的Lee等人在1998年发现了RH（recurring hump）现象，并试图据此解释同步流的散点现象［2］。后来，Kerner［3］根据实测德国高速公路的交通流数据，提出了“3相交通流理论”。由于“3相交通流理论”能够解释许多基本图方法无法解释的现象，比如“幽灵塞车”。因此，这一理论随后受到很多交通专家的研究。由于在现实情况中，测定交通流的3个参数（流量、密度和速度）比较耗时、耗力，而Vissim仿真软件能够比较准确地模拟现实中的交通流，并且比较容易模拟不同状态下的交通流。正是利用Vissim仿真软件这一特点，本文研究了仿真得到的数据与3相交通流模型的符合程度，这正是本文研究的目的。

1 3相交通流理论

3相交通流理论是由德国学者Kerner根据实测德国高速公路的交通流数据提出来的。在2004年，Kerner出版了《The Physics of Traffic》一书，该书详细地介绍了3相交通流理论，标志着3相交通流理论体系的形成。Kerner把交通流分成3种状态：自由流（free flow）、同步流（synchronized flow）和宽运动阻塞流（wide moving jam flow）。自由流和宽运动阻塞流与传统交通流理论中的自由流和堵塞没有本质上的区别，差距较大的是同步流。图1是Kerner基于多车道提出的流量－密度理论关系图。图中F线表示自由流相，宽运动阻塞出现在J线上，J线的斜率表示阻塞波向上游传播的速度，图中的二维区域表示同步流相。

图1 流量－密度理论基本图Fig.1 The theoretical diagram between flux and density from literature［4］

1.1 自由流

1.2 同步流

1.3 宽运动阻塞流

在城市道路中，受到信号交叉口车辆排队的影响，相邻2个交叉口之间车辆会出现时走时停的现象。这种交通流状态就处于宽运动阻塞流。阻塞阵面以一定的速度向上游交叉口传播，传播的速度就是图1中J线的斜率，该斜率近似为一个常数。

2 一种研究交通流演变机理的交通场景描述

交通仿真的核心要点是如何更好的模拟现实中交通流的特性，模拟越接近现实，得到的数据就会更准确地反映现实交通流的特性。本文选择2种不同的交通场景来仿真模拟。交通场景1设置的路网结构见图2，单向3车道，车道宽度3.75 m，箭头方向表示交通流的流向，图中方框表示车辆，断面AB之间的路段为数据采集路段。输入流量设置、车速分布、车种比例和路径选择见表1。

交通场景2设置的路网结构见图3，主干段单向3车道，车道宽度3.75 m；合流、分流单车道，车道宽度3.75 m。箭头方向表示交通流的方向，图中方框表示车辆，断面AB之间的路段为数据采集路段。输入流量设置、车速分布、车种比例和路径选择见表2。考虑到交通中的随机因素，设置很少的小汽车期望车速为15 km／h，并且只能选择在最右侧车道上行驶。

图2 简单路网结构Fig.2 The simple road network structure

表1 交通场景1下交通特性描述Tab.1 The description of traffic characteristics in traffic scenario 1

图3 典型路网结构Fig.3 The typical road network structure

表2 交通场景2下交通特性描述Tab.2 The description of traffic characteristics in traffic scenario 2

3 Vissim建模和参数设置

目前大多仿真软件是由国外开发的，因此软件中模型的参数是基于国外的交通特性而设计的，模型的缺省值并不符合我国的交通状况。因此，需要根据我国实际的交通运行特性，对模型中各个独立的参数进行校正。需要校正的仿真参数一般包括交通运行控制参数、交通流特性和驾驶员行为特性等［5］。参数校正的目的是使仿真输出的结果与实际调查的结果相差最小。文献［5］给出了用于一般性的仿真模型参数校正流程，本文不再赘述。根据具体的仿真模型——Vissim仿真软件，文献［5］利用正交试验，对最小车头时距、平均停车距离、等待换道时间和观察前方车辆数作了参数校正。

本文对影响道路通行能力的bx＿add（安全距离的附加部分）和bx＿mult（安全距离的倍数部分）进行了仿真标定，见图4。

图4 bx＿mult不同数值下流量图Fig.4 Flow map of different values of bx＿mult

图4表示bx＿mult不同数值对城市道路一条车道基本通行能力大小的影响。由图4可知，bx＿mult取值在0～2.75之间时，单车道的通行能力基本不随bx＿mult的变化而变化；当bx＿mult的取值大于2.75时，单车道的通行能力随bx＿mult的增大而减小。因此，在进行仿真时，需要根据道路实际的通行能力选择合适的bx＿add和bx＿mult数值，否则会造成仿真的失真。

4 交通流特性分析

交通量Q、行车速度v、车流密度K是表征交通流特性的3个基本参数。车流密度是指某一瞬间内单位道路长度上的车辆数目。交通流3参数之间的关系式

式中：Q为平均流量，veh／h；v为区间平均速度，km／h；K为平均密度，veh／km。

式中：N为路段内的车辆数，辆；L为路段长度，km。

式（1）是在最普适的情况下推导得来，没有加任何特定的限制条件，因此对于任何交通流理论都是严格成立的。交通流3参数中只要确定任意2个参数，第3个参数就会被确定。在实际应用中，常常关注流量－密度的关系或是速度－密度的关系，这样就形成了交通流3参数间的关系图。

本文中，仿真周期设为3 600 s，从第600 s开始采集数据，时间间隔为300 s。选定仿真评价的路段，利用Vissim提供的路段评价功能，采集该路段的交通量、密度和速度数据。

交通场景1下，城市快速路交通流各参数之间的散点图见图5～7。

图5 交通场景1下单车道流量－密度散点图Fig.5 Flux－density scatter plots of single lanes in traffic scenario 1

图6 交通场景1下单车道速度－密度散点图Fig.6 Velocity－density scatter plots of single lane in traffic scenario 1

图7 交通场景1下单车道流量－速度散点图Fig.7 Flux－velocity scatter plots of single lane in traffic scenario 1

由图5可知，流量、密度的数据点落在一条直线上，二者满足线性关系。随着密度的增大，流量也相应增大。仿真中不断增大输入交通量，但当输入交通量Qinput＞2 000 veh／h时，路段上采集的流量却在2 000 veh／h上下浮动，密度也稳定在35 veh／km。因此，图5中当密度ρ≈35 veh／h、流量Q≈2 000 veh／h时，流量、密度的数据点出现了聚集现象。聚集现象表明交通场景1下，自由流状态下的流量最大值约为2 000 veh／h，密度约为35 veh／km。

由图6可知，密度、速度的数据点落在一条横线上，速度不随密度的增大而变化，而是在60 km／h上下浮动。图7也能得出相似结论，速度不随流量的增大而变化，而是在60 km／h上下浮动。这说明在交通场景1下，车辆以期望速度vd≈60 km／h行驶，期望速度vd也是图5中直线的斜率。

根据仿真数据，在交通场景2下，交通流各个参数之间的散点图如8、9、10所示。

图8 交通场景2下单车道流量－密度散点图Fig.8 Flux－density scatter plots of single lanes in traffic scenario 2

图9 交通场景2下单车道速度－密度散点图Fig.9 Velocity－density scatter plots of single lane in traffic scenario 2

图10 交通场景2下单车道流量－速度散点图Fig.10 Flux－velocity scatter plots of single lane in traffic scenario 2

由图8可知，当车流密度ρ＜45 veh／km时，流量－密度的数据点基本上落在一条直线上，二者满足线性关系，当车流密度ρ≈45 veh／km时，流量达到最大值Qmax≈1 800 veh／h。当车流密度45 veh／km＜ρ＜80 veh／km时，流量－密度的数据点落在一个平面二维区域中，二者不满足一一映射的函数关系，流量是密度的多值函数。当车流密度ρ＞80 veh／km时，流量很小，密度却很大；由图9可知，车流密度ρ＞80 veh／km时，车流的速度基本在10 km／h以下，交通流处于阻塞状态。

由图8、9可知，在车流密度ρ＜25 veh／km，流量Q＜1 000 veh／h时，车流的速度基本是一个常数。该常数即是图8中直线的斜率，为车流在自由流状态下的期望车速。

图11是交通场景2条件下得到的流量－密度基本图，见图11。

5 结果与讨论

由图11可知，当车流密度小于23 veh／km时，车流处在稳定的自由流相位，流量与密度成正比关系；当车流密度处于23 veh／km～42 veh／km时，车流既可以由稳定的自由流转变成亚稳定的自由流，也可以转变成不稳定的同步流。在亚稳定的自由流状态下，在车流密度为42 veh／km时，交通量达到道路的通行能力，大约是1 750 veh／h。当车流密度大于42 veh／km时，流量与密度的数据点在一定程度上散落在平面二维区域里面，这与3相交通流中的同步流并不完全符合。分析原因如下：Vissim软件毕竟是模拟现实中的交通流，所以不可能完全再现实际交通流。因此，Vissim软件建模时需要考虑更多影响交通流的因素，以接近现实中的交通流。

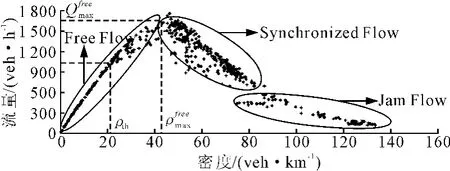
图11 交通场景2下单车道流量－密度基本图Fig.11 The basic figure of flux－density of single lane in traffic scenario 2

5.1 自由流相位

由图11可知，当车流密度ρ＜ρ（free）max≈42 veh／km时，车流处在自由流状态。当车流密度ρ＜ρth≈23 veh／km时，车流处在稳定的自由流状态；当车流密度23 veh／km＜ρ＜42 veh／km时，车流既可以处于自由流的亚稳定状态也可以处在同步流的不稳定状态。即当车流密度ρ＞ρth时，车流可能会转变成同步流也可能转变成自由流的亚稳定状态。这一现象说明自由流和同步流有重叠的区域。亚稳定状态的车流间距更小，车辆之间的相互作用增大，流量接近道路的通行能力。自由流状态的交通特性是车辆之间基本没有干扰，驾驶员都按照自己的期望车速行驶。当车流密度进一步增大，大于自由流状态下的最大密度veh／km时，车流由自由流相位转变成同步流相位。

5.2 同步流相位

由图11可知，当车流密度大于ρ＞ρ（free）max时，流量－密度的数据点一定程度地散落在二维区域中，并不完全符合同步流的特点。这一现象的原因已在上文中阐述。同步流与自由流相比，它流量较大、密度较大，但是平均速度较低。在城市道路交通流中，同步流主要由驾驶员的驾驶行为和道路交叉口引起的。在多车道的路段上，驾驶员通过不断地变换车道获得更大的行驶空间，从而车辆间的跟驰行为更加明显，车速逐渐趋于同步。在城市道路上，由于交叉口的存在，车辆遇到红灯排队产生的集结波会向上游交叉口移动；等到绿灯时，车队消退产生的疏散波也会向上游交叉口移动。这2种交通波都会引起同步流的产生。

5.3 阻塞相位

在城市快速路中，合流、分流处是道路通行能力的一个瓶颈。受合流、分流排队车辆的影响，在城市道路处于交通高峰时，合流或分流上游的车辆会出现时走时停的现象。此时，交通流处于阻塞相位。由于宽运动阻塞不会被任何复杂的交通状态捕捉，也不会被瓶颈捕捉，而且它会以一定的速度向上游传播。阻塞相位下，流量和速度很小，近乎为零，密度却很大。由图11可知，车流密度ρ＞80 veh／km时，车流的速度基本在10 km／h以下，交通流处于阻塞状态。

［1］ 徐吉谦，陈学武.交通工程学［M］.北京：人民交通出版社，2008.

［2］ 洪 昊，关 伟.交通流理论的新进展［J］.交通运输系统工程与信息，2006，6（1）：81－85.

［3］ Kerner B S.The physics of traffic［M］.Berlin：Springer，2004.

［4］ 高 坤.从基本图方法到三相交通流理论［D］.合肥：中国科学技术大学，2008.

［5］ 孙 剑，杨晓光.微观交通仿真模型系统参数校正研究：以vissim的应用为例［J］.系统仿真学报，2007，19（1）：48－50.

［6］ 赵博涵.基于三相流理论的交通流复杂动态特性的微观模式研究［D］.合肥：中国科学技术大学，2009.

［7］ 王建玲，蒋阳升.交通拥挤状态的识别与分析［J］.系统工程，2006，24（10）：105－109.

［8］ Kerner B S，Rehborn H.Experimental features and characteristics of traffic jams［J］.Phy Rev E，1996（53）：1297.

［9］ 郝 媛，孙立军，徐天东，等.城市快速路交通拥挤分析及拥挤阈值的确定［J］.同济大学学报：自然科学版，2008，36（5）：609－615.

［10］ Kerner B S，Rehborn H.Experimental properties of phase transitions in traffic flow ［J］.Phys Rev Lett，1997（79）：4030.

［11］ 王子雷，邵长桥，荣 建.城市主干路基本路段交通流仿真分析［J］.交通与计算机，2008，26（5）：6－8.