基于次优控制的汽车主动悬架道路友好性研究＊

李金辉 乐升彬 徐春旺

（1.河南科技大学车辆与动力工程学院 河南 洛阳471003；2.河南省冶金研究所有限责任公司 郑州450053）

0 引 言

汽车悬架系统作为车辆的重要部件，对于车辆的平顺性、操稳性和安全性等具有重要影响［1］。近年来，随着我国公路基础建设投资力度和运输需求的增加，重型货车在货物运输中的使用率也越来越高。重载交通加快了路面破坏，降低重载汽车对高等级公路的损伤、提高重型汽车的道路友好性，已经成为汽车设计和公路管理部门关注的热点问题。国内外相关研究表明［2－3］，合理控制悬架系统可以改善行驶平顺性并降低汽车对路面的损伤，因此，道路友好性主动控制悬架的研究就显得尤为迫切。

汽车主动悬架控制策略主要有最优控制、滑膜控制、模糊控制和神经网络控制等，在众多的控制方法中，最优控制算法比较成熟，理论基础也比较完善，是一种十分常用的悬架控制方法。严天一［4］等分析了最优控制主动悬架对道路友好性的改进效果，认为主动悬架的道路友好性优于被动悬架。然而，在实际的悬架系统设计时，考虑到状态变量的可测量性和可估计性，最优控制应用困难。基于此，有学者提出了次优控制的概念，并对次优控制主动悬架汽车的行驶平顺性进行了研究［5－6］。

为分析次优控制策略对汽车道路友好性的影响，本文基于简化的二自由度1／4车辆模型，设计了主动悬架的最优和次优控制器，考虑工程实际需要，提出了3种次优控制策略，比较分析了次优、最优和被动悬架的汽车道路友好性，以期为道路友好性悬架设计分析提供帮助和参考。

1 汽车主动悬架模型

汽车主动悬架模型有整车模型、半车模型和单轮模型等，依据本文研究的性质，为简化分析，建立如图1所示的线性二自由度1／4车辆模型。图中：ms，mt分别为车身质量和车轮质量；ks，kt分别为悬架和轮胎刚度系数；U为主动悬架力发生器所产生的控制力，cs为被动悬架阻尼系数，xg，xt，xs分别为路面激励、车身和车轮的垂向位移。

图1 汽车悬架系统模型Fig.1 Vehicle suspension system model

根据牛顿第二定律，建立图1（a）所示的汽车主动悬架系统的动力学微分方程

路面不平度的时域激励由滤波白噪声法生成，其微分方程为式中：G0为路面不平度系数；v0为车速；w（t）为零均值的高斯白噪声；f0为下截止频率；n0为参考空间频率；n0＝0．1m－1。

根据现代控制理论，结合式（1）和（2），得到主动悬架系统的状态方程为

式中：

系统状态变量

系统矩阵

控制矩阵

挠动矩阵

2 次优控制器设计

2．1 性能指标泛函

综合考虑汽车的行驶平顺性和道路友好性，用轮胎动位移xt－xg表征轮胎相对动载荷（由于Fd＝kt（xt－xg），即轮胎动载荷与动位移成正比），用车身加速度和悬架动挠度xs－xt表征汽车行驶平顺性，定义主动悬架最优控制器的指标泛函为

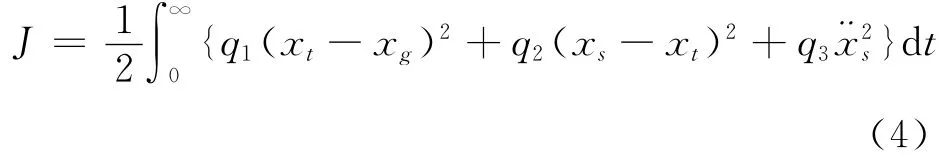
式中，q1，q2和q3分别为轮胎动载荷、悬架动挠度和车身加速度的加权系数。

2．2 最优控制器

式中，

输出矩阵

传递矩阵

将式（5）代入式（4），指标泛函进一步转化为

式中：Q＝CTq C；R＝DTq D；N＝CTq D；q＝diag（q1，q2，q3）。

由最优控制理论知，当控制器的控制力为U＝－KX＝－R－1（NT＋BTL）X 时，可使指标泛函为最小，其中矩阵L可由如下黎卡提方程求出

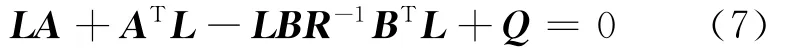
2．3 次优控制器

最优控制器是建立在系统全状态反馈的基础上的，要求系统的所有状态变量均可测或可估计，实用性较差，因此探讨悬架次优控制策略十分必要。

在最优控制的基础上，以系统的可测变量作为反馈控制量，来设计次优控制器。设系统的可测变量为Xm，则测量变量可由状态变量表示为Xm＝CmX，根据最优控制理论，此时系统的次优控制力可表示为

为得到随机次优反馈增益矩阵P，可先求出系统最优控制反馈增益矩阵Pm，然后用最小范数法得到次优控制反馈增益矩阵的近似解P。根据最小范数的定义，构造目标函数

令目标函数Jm取最极小值，便可求得次优控制反馈增益矩阵的近似解为P＝PmCTm（CmCTm）－1Cm。则次优反馈控制规律为

3 仿真对比分析

3．1 道路友好性评价指标

车辆对道路破坏潜力的大小可被定性地描述为道路友好性，破坏潜力越大，道路友好性越差。一般情况下，车辆的道路友好性可用轮胎动载荷直观评价，即较大的轮胎动载荷对路面的破坏能力强。在此基础上，国内外常用动载荷系数、道路应力因子系数，95百分位四次幂合力系数来评价车辆的道路友好性［7］。

动载荷系数克服了静态载荷评价道路友好性的缺陷，考虑了车辆与路面相互作用的动态因素，可用于评价车辆对路面的永久性损伤，其计算公式为

式中：σF为动态轮胎力标准偏差，Fs为静态轮胎力。

1958～1960年美国AASHO通过大量的道路试验得到了四次幂定律，在此基础上，1975年德国学者提出了道路应力因子的概念，并给出了其计算方法

式中：E［·］为期望运算，P（t）为轮胎瞬时动载荷，Ps为静态轮胎力，DLS为道路应力因子系数，DLS＝1＋6DLC2＋3DLC4。

考虑到轮胎动载荷的相关性和空间重复性，1996年英国学者Cole和Cebon提出了95百分位四次幂和力系数指标，即

3．2 仿真模型及参数

采用 MATLAB／Simulink软件建立相关模型并进行数据处理分析，其中主动悬架的仿真模型见图2。

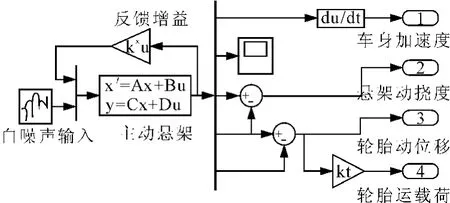
图2 主动悬架仿真模型Fig．2 The simulation model of active suspension

选用红岩CQ1163T重型货车满载时后轴单侧参数［8］，ms＝4 450 kg，mt＝550 kg，ks＝1 000 k N／m，kt＝1 750 k N／m，被动悬架阻尼系数cs＝15 k N·s／m。取常见行驶工况，B级路面，车速v0＝20 m／s，路面不平度系数G0＝64×10－6m3／cycle，下截至频率f0＝0．1 Hz。

指标泛函中各指标加权系数采用层次分析法确定，基本思路是首先消除各指标量纲上的差异，确定同尺度比例系数，然后运用层次分析法对各指标进行主观赋权，获得主观加权比例系数，最后将同尺度比例系数和指标主观权值结合，获得各指标最终权系数［9］。由于层次分析法是一种常见的指标赋权方法，本文不再赘述，仅给出利用该方法得到的指标权重q1＝127 608，q2＝54 946，q3＝l，具体过程可参考文献［9］。

鉴于工程实际中振动加速度信号较易测得，并考虑本文车辆模型状态变量的可测性，提出如下3种次优控制方案：

此方案只对车身加速度信号进行测量，并采用积分器对信号进行一次和二次积分处理。

此方案需测量车身加速度和车轮加速度信号，并分别对加速度进行一次积分处理。

此方案与方案2测量信号相同，但需要对加速度信号进行二次积分处理。

3．3 仿真结果分析

3．3．1 次优控制对轮胎动载荷的影响

图3为3种次优控制策略轮胎动载荷的幅频特性，可以看出，次优控制1与次优控制2、次优控制3的特性曲线有较大差距，特别是在轮胎共振的高频区，次优控制1的轮胎动载荷较大；次优控制2和次优控制3的特性曲线十分接近。这是由于次优控制2和次优控制3的测量变量为车身加速度和车轮加速度，而次优控制1的测量变量仅为车身加速度所致。可见，次优控制的悬架性能与测量变量密切相关，若想对高频区的车轮振动进行控制，必须对车轮加速度信号进行测量反馈，以提高道路友好性。

图4为次优控制2与被动悬架、最优控制悬架轮胎动载荷特性的比较，从图中可以看出，次优控制2与最优控制的动载响应曲线十分接近，即两者动载特性基本一致。与被动悬架相比，在车身共振的低频区，次优控制2的轮胎动载荷得到较大衰减，在车轮共振的高频区，次优控制2与被动悬架接近。

图3 3种次优控制策略的动载荷比较Fig.3 Dynamic load comparison of three suboptimal control strategy

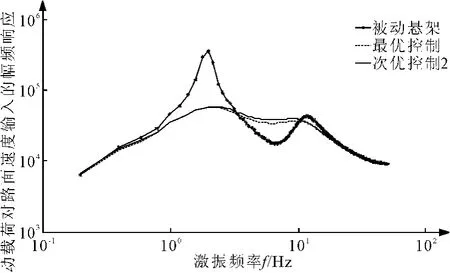
图4 次优控制对动载荷的影响Fig.4 Suboptimal control effect on dynamic load

3.3.2 次优控制对行驶平顺性的影响

为分析次优控制对汽车平顺性的影响，图5和图6分别给出了次优控制2与被动悬架、最优控制悬架车身加速度和悬架动挠度的幅频特性曲线。

图5 次优控制对车身加速度的影响Fig.5 Suboptimal control effect on body acceleration

从图5和图6可以看出，次优控制2和最优控制曲线几乎重合，即两者的隔振性能几乎相同；与被动悬架相比较，次优控制2和最优控制都有效抑制了车身加速度和悬架动挠度在车身共振低频区的振动模态，在车轮共振的高频区，三者基本持平。可见，次优控制在提高汽车道路友好性的同时，对车辆行驶平顺性也进行了较大改善。由于随机隔振的一项重要原则是尽可能降低隔振系统在低频区的幅频特性，因此，可以说次优控制的效果良好［10］。

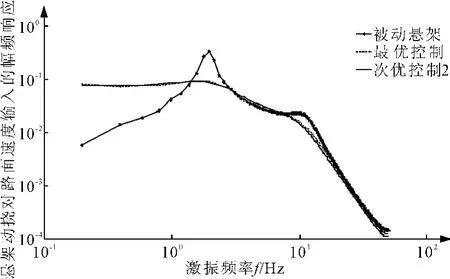
图6 次优控制对悬架动挠度的影响Fig.6 Suboptimal control effect on the suspension dynamic deflection

3.3.3 次优控制对道路友好性的影响

采用前述的道路友好性评价指标，比较各类型悬架系统对道路友好性的影响，见表1。可以看出，3种次优控制策略的道路友好性指标均小于被动悬架，且接近于最优控制悬架。在3种次优控制策略中，次优控制2的指标最小，即道路友好性最小，可见，对于本文的三种次优控制策略，方案2为较好的道路友好性控制方案。

表1 道路友好性指标的比较Tab.1 Comparison of road－friendliness index

4 结 论

1）基于悬架参数的可测性，设计了随机次优控制器，分析比较了被动悬架、最优控制悬架和次优控制悬架的道路友好性，结果表明，选取合适测量变量的次优控制悬架与最优控制悬架的道路友好性十分接近，且均优于被动悬架。

2）不同次优控制策略对悬架性能的影响不同，在悬架系统设计时，必须兼顾车辆道路友好性和行驶平顺性等多方面的特性，针对不同的次优控制策略进行优选。

3）对于实际的车辆悬架系统，最优控制由于受状态变量测量方面的限制，难以在实际中得到广泛应用，即使所有的状态变量都可以通过一定的后处理方法得到，也会带来测量机构复杂、测量成本高等问题，而立足于简单、实用、高效原则的次优控制方法更具有现实意义。

［1］ 张立军，何 辉.车辆行驶动力学理论及应用［M］.北京：国防工业出版社，2011.

［2］ Pable M J，Gawture M M，Seshu P.A review of‘Road－Friendly’suspensions［J］.Proceedings of 13th NaCo MM07，2007，1（1）：12－13.

［3］ Valásˇek M，Kortüm W，Sˇika Z，et al.Development of semi－active road－friendly truck suspensions［J］.Control Engineering Practice，1998，6（6）：735－744.

［4］ 严天一，刘大维，陈焕明，等.基于主动悬架系统车辆的道路友好性［J］.机械工程学报，2007，43（2）：163－167.

［5］ 董小闵，余 淼，廖昌荣，等.汽车磁流变半主动悬架频域加权次优控制研究［J］.系统仿真学报，2006，18（11）：3183－3186.

［6］ 张玉春，丛 华，王良曦，等.基于1／2车辆模型的主动悬挂滤波输出反馈控制研究［J］.公路交通科技，2004，21（6）：121－126.

［7］ Potter T E C，Cebon D，Cole D J.Assessing＇roadfriendliness＇：a review［J］.Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，1997，211（6）：455－475.

［8］ 陈一锴，何 杰，李旭宏，等.基于模糊控制的重型货车空气悬架性能多目标优化［J］.东南大学学报：自然科学版，2008，38（2）：319－323.

［9］ 柴陵江，孙 涛，冯金芝，等.基于层次分析法的主动悬架 LQG控制器设计［J］.汽车工程，2010，32（8）：712－718.

［10］ 顾仲权，马扣根，陈卫东.振动主动控制［M］.北京：国防工业出版社，1997.