一种基于视频序列的城市快速路交通状态分类方法＊

张 媛 贾克斌

（北京工业大学电子信息与控制工程学院 北京100124）

0 引 言

近年来交通的现代化带来了很多问题：道路拥挤、事故增加、交通环境恶化，等等。智能交通系统在这样的情况下应运而生，它是将应用信息、通信、计算机、自动控制等技术集成而建立起的一种高效、便捷的交通运输综合管理和控制系统［1］。交通状态的有效分类是ITS非常重要的子系统和功能之一［2］。

目前，国内外的交通状态识别研究主要是基于先进的信息采集技术。采集的实际交通参数，如速度、流量、占有率等，结合交通流理论和模式识别的方法，进行路段的交通状态的识别。但是这些方法的有效性一方面依赖于交通参数采集的准确性和实时性；另一方面取决于分类方法选择的合理性。很多实验表明，这些方法在交通处于拥堵状态下交通参数检测准确率急剧下降。

近年来，随着机器视觉技术的发展与广泛应用，国内外学者提出了一系列基于视觉特征与模式识别的交通状态识别方法。该方法主要分为2类，第一类为视觉特征的直接判别方法，基本思想是从视频帧中提取特征直接检测交通状态。如Xiaokun［3］和Porikli［4］最早利用基于 MPEG 视频图像的DCT系数和运动向量构成的特征向量，由高斯混合隐马尔可夫模型进行交通状态分类。但是，交通状态有一定持续期，单帧图像的交通密度不足以对交通状态准确分类［5］，同时利用隐马尔科夫模型分类是非常复杂的。

第二类方法为根据视频序列的特定区域或虚拟检测线上像素内容随时间的变化，构建描述一定时间段内车辆运行状况的图像，然后采用图像处理算法，提取特征判断交通状态。这种时空信息目前主要用于对车辆的检测，如Zhu等［6］在时空图像中定义全景图（PVI）及核线图（EPI），根据二者的差异来检测车辆，A.Liu［7］则利用背景消减与时空图像相结合来完成车辆的最优检测。与本文工作相近的是Daeho Lee［8］等人将时空线序列图像PVI和EPI应用于交通状态分类，不过他们仍然进行的是交通参数提取工作；而文献［9］提出了一种基于单车道感兴趣区域的时空描述符的交通状态识别方法，把一定时间段的时空图像进行叠加，将交通状态分为2类（流畅、拥堵），实验证明该方法受环境因素的影响较小，但是直接将图像进行叠加，仍然产生背景变化因素会直接影响分类结果。

与以上工作不同，本文提出一种基于时空线序列符和主成分分析（principal component analysis，PCA）对交通状态进行分类方法，首先在视频序列中提取时空信息，该信息具有丰富的时间、空间二维特性，可以很好的表征当前交通状态。该方法在拥堵状态下能够很好的完成交通状态的识别，由于是基于“线”的叠加而非图像的叠加，因此不存在因为背景更新而引入的问题。然后对该信息通过PCA进行降维和特征提取，最后用支持向量机（support vector machine，SVM）来完成分类与识别工作。整体流程见图1。

图1 方法流程图Fig.1 Overall flow chart

1 时空线序列符

首先，在视频原图像中设置1条虚拟时空线，如图2中视频序列中的实线所示，将每帧图像中虚拟时空线上的像素值记为行向量Lt，如式（1）。式中：p为线段上的点。然后将t－N＋1帧到t帧视频序列中的该行向量进行叠加得到当前时刻的时空线序列符St，如式（2）。

由此可以看出，每个时空线序列符都是一个W×N的矩阵。其中：W为所设定的时空线序列符的宽度；N为所选取的进行叠加的视频帧数，为事先定义好的参数。在此基础上定义延迟线结构（见图3）从而得到全部的时空线序列符组合U：

式中：M为获取的时空线序列符的样本。

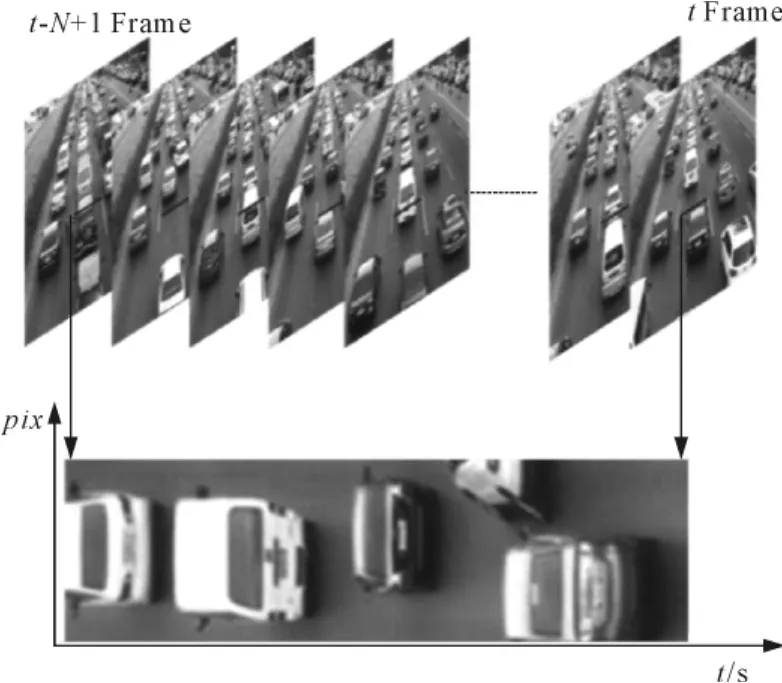
图2 时空线序列符的获取Fig.2 Setting line and generation of time－spatial image

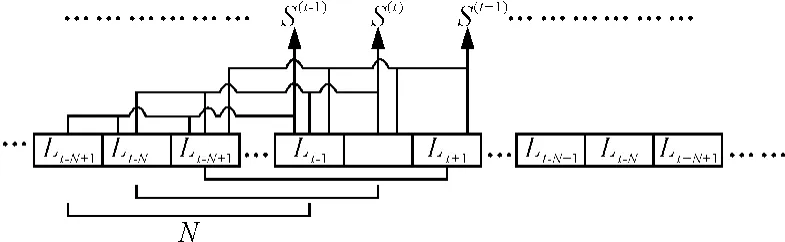
图3 延迟线结构Fig.3 Delay－line structure

由定义可知，时空线序列符反映了特定区域（虚拟时空线）的图像灰度值随时间变化的特性，可以很好的映射出当前的交通状态。当交通状态流畅时，车行速度较快，车身通过虚拟时空线的时间较短，表现为单个车辆在时空线序列符中所占的“时间块”较小。反之，当交通状态拥堵时，车速较慢，单个车辆在所占的“时间块”较大。因此，本文所设定的时空线序列符可以作为衡量交通状态的表征。

此外，本文所定义的时空线序列符实际上为指定线段在时空上的积累，因此产生的为虚拟的“背景”，是该线段在N帧视频序列所代表的时间上的延伸表现，并没有实际意义上的背景，从而有效避免了由背景的引入而带来的更新、噪声等问题，所以与基于感兴趣区域定义的时空区域信息相比，降低了数据的复杂度。

2 数据降维处理——主成分分析（PCA）

时空线序列符是由二维特征矩阵表示的对象，特征之间难免存在重叠、相关的关系。可以观察到，除去车辆本身及各车辆之间的相对位置信息，其余部分均为虚拟“背景”，存在大量的数据冗余.因此需要对其进行主成分提取。以时空线序列符为例，介绍二维图像经典的PCA算法步骤如下。

由式（2）已知：

1）行堆叠样本，S′为堆叠后结果：

2）计算样本均值Ψ及各样本与其的差值di：

3）构建协方差矩阵C，如式（8）。式中：A为式（9）。用奇异值分解法求解AAT的特征值λi及应的特征向量vi，然后在此基础上计算贡献率φ，见式（10），通常α＝0．9。最后求出C的特征向量ui，见式（11）。

4）获得样本特征空间r，并将样本映射到特征空间从而得到训练的数据样本S″i，如式（13）。

5）将任何一幅时空描述符映射到特征空间

在此基础上，2DPCA的基本思想是将图像矩阵S通过Y＝SX映射到X上，从而Y成为S的投影特征向量，X采取如下投影准则：使得J（X）＝最大化。其中：Gt如式（15）所示，其中表示为所有图像的均值

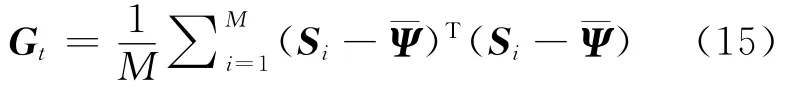
取得Gt的最大的d个特征值对应的特征向量即可实现最佳投影。该算法实质为对图像仅仅在列方向上消除相关性，因此，可以对图像在行方向上做同样的运算，即为双向2DPCA算法，记为LR2DPCA。

LR2DPCA将行或列分立为2个独立的方向单独考量。但大量的信息存在明显的空间重复性。因此可将LR2DPCA方法与PCA方法相融合，在LR2DPCA的结果之上再进行一次PCA，从而最大程度的提高压缩率以及减少计算量。

3 基于支持向量机（SVM）的分类方法

进过降维的特征矩阵仍然具有较高复杂度，存在线性不可分的情况。SVM在解决非线性及高维模式识别中表现出许多特有的优势，能保证找到全局最优解，所以选取SVM来作为交通状态的分类器。

SVM由线性分类发展而来，因此我们从线性分类出发来介绍分类的基本原理。

3．1 线性分类

给定样本数据空间（xi，yi），i＝1，2，…，M，其中xi∈Rd，yi∈｛－1，1｝为估计输出量，线性判别函数表示为式（17），其中ωT为权向量，b∈R为偏置。

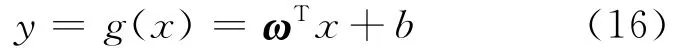
如图4所示，H为分类超平面。样本点到超平面的间隔设为δ，由解析几何可知分类间隔为1／‖ω‖。最大化分类间隔是包括SVM在内的所有线性分类的思想。因此求得满足约束条件（17）的‖ω‖的最小值即可获得最优超平面。求解过程如下。

图4 分类超平面示意图Fig．4 Classification hyperplane

约束条件：

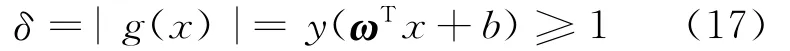
1）引入拉格朗日函数式（18），｛αI，i＝1，2，…，M，αi≥0｝为拉格朗日乘子。

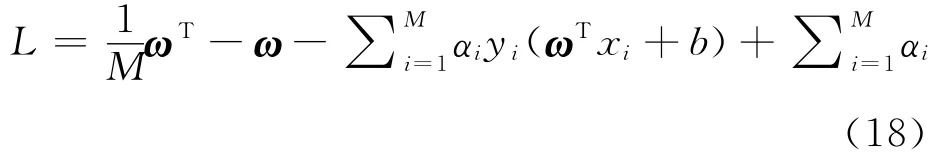
2）L在鞍点处对ω和b取最小值，对αi取最大值可得对偶形式（19）。根据Kuhn－Tucker条件函数最优解满足式（20）。当满足条件时，αi＝0，反之αi≥0。

3）msv表示满足条件样本点个数；b可由这些样本点的Kuhn－Tucker条件式求和获得：

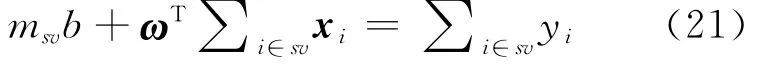
在实际问题中，各类数据存在离群点，因此引入2个变量：松弛变量ξ以及惩罚因子C，常在式（19）后加入经验误差项详情请参见文献［10］。

3．2 非线性分类

时空线序列符的特征空间维数较高且线性不可分，SVM 通过一个非线性映射，如式（22），可将数据映射到高维空间，然后在高维空间内做线性回归。此时拉格朗日对偶形式变为（23）。

这种变换看似复杂，但是对于样本寻优及分类函数仅只涉及样本间的内积运算。根据泛函相关理论，只要核函数k（xi，xj）满足 Mercer定理就可以对应某一空间中内积，如式（24）。从而选取合适核函数就可以实现某一非线性变换后的线性分类，常用的核函数有以下几种。

多项式核函数

高斯径向基函数

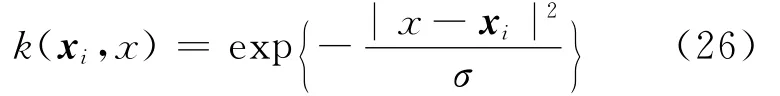
Sigmoid函数

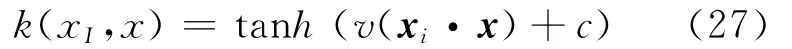
4 实验结果及分析

综合考虑视频拍摄和信息提取的复杂性与有效性，本文选择城市快速路的基本路段作为研究背景和实验样本采集来源，并参考S．Bassan［11］等学者提出两相交通流分类法，在样本训练阶段通过主观判断加客观估计的方法定义如下2种交通状态：

1）畅通。在一定的时间段内，目标道路上的车速非常快并且车辆的数目非常少。

2）拥堵。在一定的时间段内，目标道路上的车速非常慢并且车辆的数目非常多。

本文实验视频数据集均来自于北京市快速路。视频包括从09：00～18：00时不同时段的道路交通状况，总共5段，每段时长60 min。原始视频的清晰度是720 480，视频的帧率为29帧／s。因此总共有29×3 600×6＝5 400 000帧。

选取虚拟时空线宽度为91，并叠加10 s内图像，可得时空线序列符为290×91的图像矩阵。共有540 000－29×10＋1幅时空线序列符。

图5标明了在2种交通状态下提取的时空线序列符的对比。其中（a）、（b）为畅通状态，（c）、（d）为拥挤状态。实验结果很好的论证了2．1中的分析：即车辆所占“时间块”的大小可以很好的表征当前的交通状态。图5（d）可以给出更加形象的描述，在极度拥堵状态下，车速几乎为0，因此车辆的某一位置始终占据虚拟时空线，线上将近10 s内容相同，从而车辆被显著“拉伸”。同理，当交通状态非常畅通，车辆以不超过限速的最大速度行驶，车头与车尾通过时空线的时差达到最小，它们在序列符中的相对位置最近接近，从而车身最短，达到车辆被“压缩”的视觉效果。

图5 畅通、拥堵状态下的时空线序列符提取结果Fig．5 Time－spatial image under smooth flow and congestion

4．1 主成分提取结果

在所获得的时空线序列符集中，各选取畅通和拥堵状态下600幅典型图像作为样本数据集，对所有样本以式（11）中的方差累计贡献率α＝0．9为条件，进行如下4种变换来提取主分量：PCA、2DPCA、双向2DPCA（LR2DPCA）、双向2DPCA与PCA融合算法（2DPCA＋PCA），样本原始维度为：290×91＝26 390。

对于算法的压缩性能，分别从压缩后维度、压缩率，重构精确度3个方面来进行评价。压缩的目标就是在保证重构准确度的同时，使得压缩率尽可能的大。

1）压缩后维度D。如在式（12）中的p以及2DPCA中的W×d。

2）压缩率η。即样本被压缩消除的维度与样本原始维度之比，即η＝（1－D／W×N）×100%。η越大，压缩性能越好。

3）重构准确度。定义β为实际贡献率，当为PCA或2DPCA方法时β＝φ；当为LR2DPCA时，β＝φlpca·φrpca；当为 LR2DPCA＋PCA 方法时，β＝φlpca·φrpca·φpca。β越大，表明压缩结果保留的信息越丰富。

各方法压缩结果及对比详见表1。

表1 各种主成分分析算法详细结果Tab.1 The results and comparison of PCA

由上述结果可以看出：PCA的压缩效率优于2DPCA、LR2DPCA，而 实际运算中 2DPCA、LR2DPCA计算量要远远小于PCA。而LR2DPCA与PCA融合方法结合了PCA与2DPCA的优点，可以在减小计算量的同时，达到最高的压缩性能。

此外，一般情况下，当重构准确率越高，应保留越多的原始信息，从而压缩率应越小，这一点在2DPCA与LR2DPCA＋PCA方法上得到很好的印证。但是，注意到PCA的压缩率和重构准确度均高于LR2DPCA，可有以下解释：LR2DPCA将行与列独立开来做主成分提取，因此并不考虑这2个分量之间的相关信息，例如在表征行列关系上很重要却在单独的行或列内贡献率很小的分量被滤掉，或者行和列之间仍然存在较大的相关性和数据冗余。这便导致LR2DPCA提取出的的分量效率低于PCA的结果。在LR2DPCA＋PCA中仍然存在这个问题，该方法消除了如上讨论的第2种情况，单仍无力弥补第1种情况带来的损失。

因此在实际运用中，需要根据实际需求综合考虑压缩率与重构准确度的表现选取合适的PCA算法。本文对压缩图像做重构图6所示，其中上下2个虚线框分别代表畅通和拥堵状态，从左到右分别为原始图像，PCA、2DPCA、LR2DPCA、LR2DPCA＋PCA的重构效果。其中，重构方法为投影矩阵与特征矩阵再加上样本均值。以PCA为例，重构公式为式（28），各参数注解见2.2。

图6 各种PCA算法重构效果图Fig.6 The reconstruction of PCA algorithms

由重构效果可知，在LR2DPCA＋PCA的重构准确度下，2种交通状态仍然有较为明显的可分性。从而本文选取双向2DPCA与PCA的融合算法。

4.2 基于SVM的交通状态分类结果

本文选取3.1经过主成分提取的600×2＝1 200幅图像作为训练阶段的样本，即SVM分类器的输入。并手动输入图像类别：将畅通状态的类别标签设为1，拥堵状态的类别标签设为2。另外选取畅通和拥堵状态下的各500幅图像作为测试图像进行分类。

实验采用台湾大学林智仁（Lin ChihJen）等开发设计的SVM模式识别与回归的软件包，考虑线性不可分情况，建立的非线性软间隔分类器，即聚类支持向量机（C－SVM）来对数据进行离线训练和预测。

4.2.1 数据规范化处理

将数据映射到特征空间后，数值范围变动较大，不便于提高处理的速度和准确度，因此采用最小－最大规范化对原始数据进行线性变换，归一到［－1，1］范围内，见式（29）。式中：xmin、xmax分别为数据集中的最大、最小值。

4.2.2 核函数选择

由训练样本集和核函数完全描述。而如何选择核函数迄今没有完备的参考和证明。本文采用常用核函数进行实验，结果见表2。

表2 不同核函数分类对比Tab.2 Classification under common kernel functions

表中正对角线上数值越大，标明分类效果越好。通过对比结果，发现采用高斯径向基函数作为核函数在识别率和识别时间上均显示出明显的优势。因为本文模型设计使用径向基函数为最理想选择。

由式（23）和文献［12］中可知，C取大值时对训练数据拟合度高而泛化能力差，γ增加时支持向量个数减少，回归曲线变平缓却会降低回归估计的精度。因此在训练过程调整参数C和γ值，当C＝4，g＝0.012时达到最优结果。

4.2.3 与其它分类器对比

为了更好的体现SVM在模式分类与识别上的优越性，本文同时选取多层感知器神经网络（multilayer perceptron，MLP）分类器、Bayes分类器以及RBFNetwork算法对2种交通状态进行分类与对预测。为保证实验结果的可对比性，以上所有算法均在本文提供的相同样本集内进行，准确率比较见表3、4。

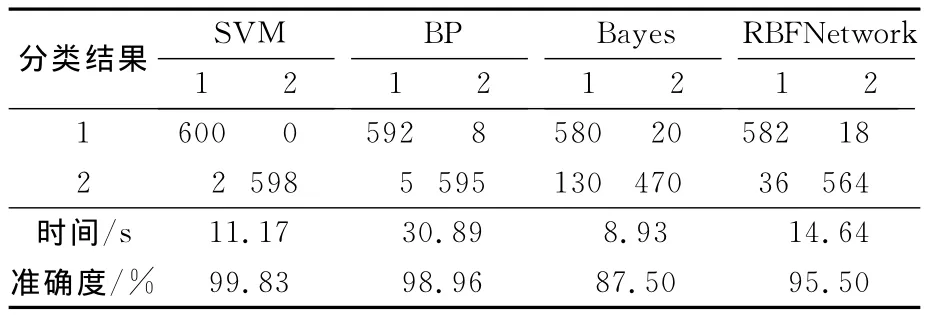
表3 不同分类器对样本分类结果对比Tab.3 Classification of different classifier

由表3可知，SVM算法与BP神经网络的分类与预测错分率是最优的，但是BP建模时间过长；而Bayes的建模时间较短，但是精确度无法达

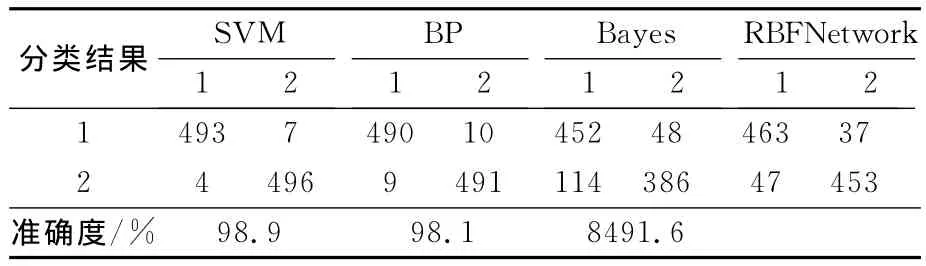
表4 不同分类器对测试样本预测结果Tab.4 Forecast of different classifier

到要求。RBFNetwork在2个参数上均低于SVM。综上，SVM从时间、准确率和实际效果方面对比，基于SVM的交通状态分类最具优势。而表4的结果表明，SVM对于测试样本的预测性在几种分类器中也达到了最优效果。因此，SVM在基于时空线序列符的交通分类方法中性能达到最优。

5 结束语

介绍了现有交通状态分类方法并简要分析了它们的劣势和不足，并在此基础上提出了一种基于时空线序列符和主成分分析的交通状态分类方法。首先介绍了时空线序列符、主成分分析、SVM的算法原理。然后从视频序列中提取时空线序列符，根据该图像的特征以及实验结果选取双向2DPCA与PCA融合的方法对其进行降维与特征提取。最后采用高斯径向基核函数进行线性变换，通过对样本数据离线学习确立最优参数，建立交通状态分类模型，并将分类结果分别与BP、Bayes和RBFNetwork 3种常用的学习训练算法对比，实验结果表明根据由SVM建立的模型在交通状态分类上具有较高的准确率和时效性。

［1］ 王国锋，宋鹏飞，张蕴灵.智能交通系统发展与展望［J］.公路，2012（5）：217－222.

［2］ 陆化普.智能交通系统的智能化：关键技术与发展展望［J］.综合运输，2012（3）：11－16.

［3］ Li Xiaokun，Porikli F M.A hidden markov model framework for traffic event detection using video features［C］∥International Conference on Image Processing，ICIP 2004，Singapore，IEEE.2004：2901－2904.

［4］ Porikli F M，Li Xiaokun.Traffic congestion estimation using hmm models without vehicle tracking［C］∥IEEE Intelligent Vehicles Symposium，Parma，Italy：IEEE，2004：188－193.

［5］ Ko J，Guensler R L.Characterization of congestion based on speed distribution：a statistical approach using Gaussian mixture model［C］∥Transportation Research Board Annual Meeting，Washington DC.：Transportation Research Board，2005.

［6］ Zhu Z，Xu G，Yang B，et al.VISATRAM：A realtime vision system for automatic traffic monitoring［J］.Image and Vision Computing，2000，18（10）：781－794.

［7］ Anan L.Video vehicle detection algorithm based on virtual－line group［C］∥Circuits and Systems，2006.APCCAS 2006.IEEE Asia Pacific Conference on.Singapore：IEEE，2006：1148－1151.

［8］ Lee D，Park Y.Measurement of traffic parameters in image sequence using spatio－temporal information［J］.Measurement Science and Technology，2008，19（11）：115503.

［9］ 李卫斌.基于视频的快速路交通状态判别及交通参数获取方法研究［D］.北京：北京工业大学，2011.

［10］ 郑逢德.支持向量回归算法及应用研究［D］.北京：北京工业大学，2012.

［11］ Bassan S，Faghri A，Polus A.Experimental investigation of spatial breakdown evolution on congested freeways［J］.Civil Engineering and Environmental Systems，2007，24（4）：261－274.

［12］ 曹成涛，徐建闽.基于PSO—SVM的短期交通流预测方法［J］.计算机工程与应用，2007，43（15）：12－14.