基于复杂网络理论的长沙市公交网络拓扑性质研究

唐秋生 冯海峰 李 维

（1.重庆交通大学交通运输学院 重庆400074；2.东南大学交通运输学院 南京210096）

近几年里，复杂网络理论［1］在基础科学研究和实际应用上都取得了惊人的进展，但关于城市交通网络的复杂性研究才刚刚开始，很多文献指出了城市交通网络复杂性问题的研究方向［2］，这对城市交通系统复杂性的研究具有重要指导意义。本文综合利用复杂网络理论［3］，讨论长沙市公交网络拓扑结构，从网络拓扑结构出发，分析当前公交网络对公共交通的影响，并证明了长沙市公交网络为小世界网络。本文研究的的基础数据包括122条公交线路，1 016个停靠站点，其中包括城区线路115条、旅游和立珊线路4条、星沙线路3条。

1 公交站点复杂网络

为研究公交站点之间关系，建立停靠站点的复杂网络，建模方法为：顶点是公交汽车的停靠站点，如果存在1条公交线路同时经过2个站点，且该线路在这2个站点之间没有其他站点（即2站点在线路上相邻），则在这2个站点间连一条边［4］。利用Pajek得到站点网络图，见图1。

图1 公交站点网络图Fig.1 Bus stations network diagram

节点度值分布表，见表1。

表1 公交站点网络度分布表Tab.1 Bus stations network degree distribution table

对实际数据的计算分析，得到长沙市公交站点网络在双对数坐标下度分布图，见图2。

图2 度的对数分布Fig.2 Degree of logarithmic distribution

由图1可见，长沙公交站点网络度分布通过直线y＝－2.798x＋2.695拟合（R2＝0.853）。由此可知网络度分布大体上服从幂率分布［5］，长沙公交站点网络为无标度网络［6］。通过计算可得长沙公交站点网络的平均路径长度为16.72，网络中2站点间最大距离为60（望城汽车站 （686）和黄花机场（1 000）），长沙公交站点网络2点最短路径的分布曲线呈钟形，经拟合发现，服从Weibull分布（其中R2＝0.973）。有关研究表明：北京公交站点网络任意2个站点之间的平均最短路径为17.387，最远的距离是103站［7］。

图3 平均路径概率密度曲线Fig.3 The average path probability density curve

一个节点i的聚类系数是指它所有相邻节点之间连边数目占可能最大连边数目的比例，公式为

式中：aij为邻接矩阵元，当节点i，j相邻时值为1，否则为0［8］。聚类系数刻画节点邻居间联系紧密程度。整个网络的聚类系数就是所有节点的聚类系数Ci的平均值。

通过计算可得长沙市公交站点网路的平均聚类系数为0.032 7，具有明显的聚类效应［9］，故该网络为小世界网络。其分布见图4。

图4 聚类系数概率分布图Fig.4 Clustering coefficient of probability distribution

2 公交线路复杂网络

为了研究各条公交线路之间的关系，构造1个公交线路复杂网络，顶点是公交线路［10］。如果2条公交线路有相同的停靠站点，则在2个顶点之间连接1条边。结果表明在长沙市的公交系统中，有一些线路和其他绝大多数线路都有重复的停靠站点，这些线路在公交系统的可达性方面起到了重要的作用。同时，也有线路和其他线路的停靠站点有上千次的重复，这也反映了该条线路所经过的站点具有相对重要的作用。

通过Pajek软件辅助计算，可以得出网络的度分布，见图5。

图5 公交线路网络度值对数分布Fig.5 Bus lines network value of logarithmic distribution

在半对数坐标上接近直线y＝－1.022 2x＋2.672 8。网络的平均节点度为27.2，即在本文设定的网络中平均每条公交线路在该线路的各个站点上总共与27条其他公交线路相交。

节点度越大的节点与其他线路相交的可能性越大，在公交换乘中所起的作用就越重要［11］。如202路等公交具有较大的节点度，说明与其在不同站点相交的公交线路较多。网络的连通度为100% ，说明在这122条线路中不存在孤立的节点，每条公交线路都可以通过其他的线路进行换乘。最短路径长度集中在1～4之间，并且网络的群聚系数较大，可以看出该网络具有很好的小世界特性。

3 公交换乘复杂网络

换乘情况是公交系统可达性的1个重要指标［12］。为此建立公交换乘复杂网络，其顶点是停靠站点。如果站点之间有同1条公交线路通过则有1条边连接。这种方式构成的网络是1个无权网，且同1条公交路线上的各个站点之间是完全连接的。这种方式建立的网络要比之前建立的站点网络大的多。

经分析得出该网络的平均节点度为117.62。具有最大节点度的节点是长沙火车站，其度为569。由此看出该站点对于长沙市公交网络来说是一个很重要的中心枢纽。度的分布可以用一个幂次函数p（k）～k－s来描述。对实际数据的计算分析，得到才长沙市公交站点网络在双对数坐标下度分布图，见图6。

图6中显示长沙公交站点换乘网络度分布通过直线y＝－1.417x＋3.771拟合（R2＝0.892）。由此可知网络度分布服从幂率分布，长沙公交站点网络为无标度网络。

图6 公交换乘网络度对数分布Fig.6 Transit network degree of logarithmic distribution

根据统计数据，公交站点全连通网的平均最短路径为2.165 63，即长沙市居民每次出行平均需要换乘公交车1.165 63次。这里没有考虑轨道交通，只是单纯的公交换乘。其概率分布，见图7。

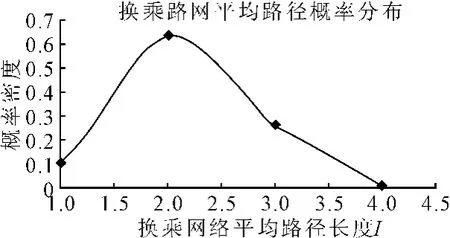
图7 换乘网络平均路径概率分布Fig.7 The average path probability distribution of Transit network

4 城轨网络对公共交通的影响

将长沙市规划中的轨道1号线和2号线叠加到现有的公交网络中，得到的指标分析如下。图8为叠加网络度值概率分布。

图8 叠加网络度值概率分布Fig.8 Overlay network value of probability distribution

公交网络平均节点度＜k＞＝3.74，叠加网络的平均节点度＜k＞＝5.1。平均节点度的增大意味着网络中边的数量增加，交通流对路径可以有更多的选择，有利于分散网络的流量和压力［13］。

2个网络产生的平均路径［14］长度概率分布图形状相似（见图9），公交网络中大多数路径的长度集中在11～17之间的概率比叠加网络的要低一些。公交网络的平均路径长度＜d＞＝16.72，而叠加网络的平均路径长度降低到＜d＞＝11.91。这表明，城轨网络在公交网络的一些不具有连通性的关键点上提供了连通性，从而显著降低了网络的平均路径长度。

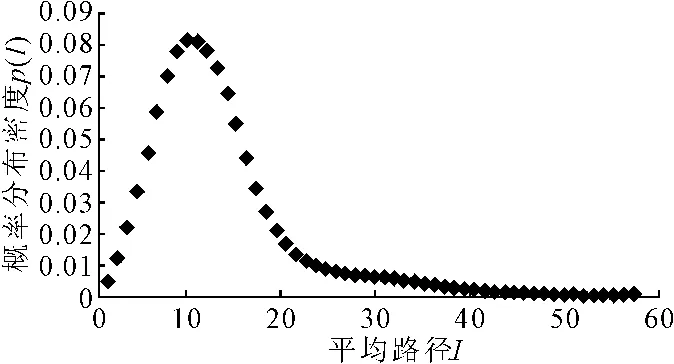
图9 叠加网络平均路径概率密度曲线Fig.9 The average path probability density curve of overlay network

对公交网络和叠加网络的分析还表明，叠加城轨网络后，网络的簇系数值C有所下降，由0.037 2下降到0.030 2。复杂网络的研究成果已经表明，规则网络和小世界网络具有大的簇系数，随机网络的簇系数较小［15］。由此，叠加网络的簇系数下降，说明网络的随机度增大、异构性减小。

图10 叠加网络聚类系数分布Fig.10 Clustering coefficient of probability distribution of overlay network

5 结束语

本文分析得到长沙公交网络为小世界网络，但是，居民从某一站点到达另一站点却需要16～17站的距离，而且换乘1.1次，由此得出：虽然目前的公交网路为小世界网络，但其网络联通率还需要有关部门的进一步优化，从而满足居民出行。

［1］ 赵 月，杜 文，陈 爽.复杂网络理论在城市交通网络分析中的应用［J］.北京：城市交通，2009（1）：57－63.

［2］ 常 鸣，马寿峰.我国大城市公交网络结构的实证研究［J］.系统工程学报，2007，22（4）：412－418.

［3］ 马杰良，安莉莉，刑 雪.城市公交网络的拓特性分析［J］.山西：山西师范大学学报：自然科学版，2009，23（1）：51－55.

［4］ 刘 锐，严宝杰，黄志鹏.城市公共交通网路的复杂性分析［J］.交通运输系统工程与信息，2009，9（3）：17－22.

［5］ 杨 扬.北京市公共交通网络复杂性分析［D］.北京：北京交通大学，2011.

［6］ 李 英，周 伟，郭世进.上海公共交通网络复杂性分析［J］.系统工程，2007，25（1）：38－41.

［7］ 王 喆，彭其渊.成都市公交复杂网络拓扑特性研究［J］.交通与计算机，2007，25（2）：39－42.

［8］ 胡一竑.基于复杂网络的交通网络复杂性研究［D］.上海：复旦大学，2008.

［9］ 赵金山，狄增如，王大辉.北京市公共汽车交通网络几何性质的实证研究［J］.复杂系统与复杂性科学，2005（2）：49－52.

［10］ 赵俊红.天津市公共交通网络复杂性研究［D］.天津：天津大学，2010：20－69.

［11］ 沈 波，刘 云.城轨网络对北京公共交通的影响研究［J］.都市快轨交通，2008，21（1）：44－46.

［12］ 胡君辉，徐新平，杨永栩.三组城市公共汽车运输网的小世界性质［J］.广西师范大学学报：自然科学版，2006，24（2）：13－17.

［13］ 薛惠锋，王媛媛，闫 莉，等.西安公交站点网络的实证研究［J］.西安工业大学学报，2008，28（5）：67－70.

［14］ 刘煡香.复杂网络理论及其在国内研究进展的综述［J］.系统科学党报，2009，17（4）：33－39.

［15］ 高自友，赵小梅，黄海军，等.复杂网络理论与城市交通系统复杂性问题的相关研究［J］.交通运输系统工程与信息，2006，6（3）：45－51.