基于风能转换系统的模糊PID自适应控制

李意扬， 吴定会

(江南大学电气自动化研究所，江苏无锡214122)

发生在日本的核电站泄漏灾难，将人们的关注度从高风险的核能源和石化能源技术转移到可再生能源上。风力发电，由于其技术成熟，污染小，能有效缓解能源匮乏，改善能源结构，正越来越受到世界各国的重视，并得到了广泛的开发和利用。

由于空气动力学的不确定性和机械、发电机模型的复杂性，必然导致风能转换系统是一个复杂的非线性系统，难以建立其精确的数学模型。如何将获得的风能最大程度地加以利用，引起了众多学者的重视［1］。

在众多的控制方法中，PID算法虽然其结构简单，但其实施方便，工业上90%的控制回路均采用以PID控制为基础的常规控制。传统PID参数整定非常直观，有响应曲线法［2］、极限环振荡法［3］，和飞升曲线法［4］，但参数单一，不能适应复杂非线性的风能转换系统。为此，有的学者试图增加参数的多样性，如文献［5］提出利用带有不灵敏区的分段PID控制策略以补偿对象的非线性。文献［6］和文献［7］则采用基于自抗扰控制理论的鲁棒控制，以提高系统的不灵敏度为宗旨来抵御不确定性，取得了较好的效果。

以上所述的方法本质上都属于传统控制，不能摆脱精确模型的限制，受文献［8］启发，文中给出了变速恒桨距风力发电系统模糊自适应整定PID控制方案，并仿真比较了不同隶属度函数对结果的影响。与传统控制相比，模糊控制对于环境和任务的复杂性有更大的适配度，它不仅对于建立的风机模型，而且对于快速多变的风场有着极强的自适应能力。

1 双馈风能转换系统建模

如图1所示，风能转换系统主要由4个部分组成:风轮机、传动系统、双馈发电机和电网连接系统。

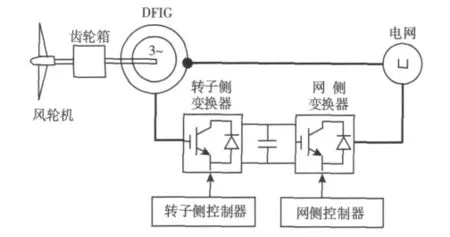
图1 双馈风能转换系统结构Fig.1 Structure of WECS based on DFIG

1.1 风轮机模型

由贝兹定理可知，风力机的机械功率为

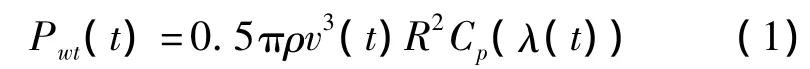
式中，ρ为空气密度，v(t)为风速，随时间变化，R为风轮半径，Cp(λ(t))为风能转换系数，是λ(t)的函数。风轮叶片的叶尖线速度与风速之比称为叶尖速比 λ(t)，即 λ(t)=Ωl(t)·R/v(t)，Ωl(t)为风轮旋转的机械角速度。

风轮机产生的风力矩

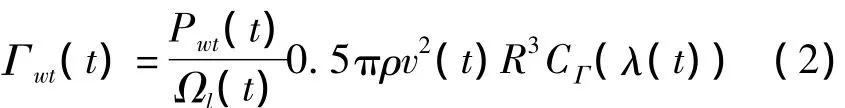
CΓ(λ(t))为转矩系数，CΓ(λ(t))=Cp(λ(t))/λ(t)。转矩系数可用以下多项式得出:

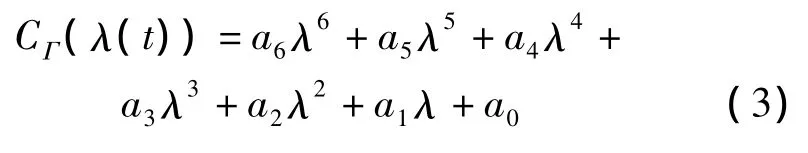
参数 ai=0，1，…，6，通常由实验数据得来，文中 a0=0.006 1，a1= －0.001 3，a2=0.008 1，a3=－9.747 7 × 10－4，a4= － 6.541 6 × 10－5，a5=1.302 7 ×10－5，a6= －4.34 ×10－7。

1.2 传动系统模型

传动系统主要由低速轴、变速齿轮箱、高速轴组成，低速轴连接风轮，高速轴连接发电机转子，低速轴到高速轴由变速齿轮箱连接。忽略黏性摩擦，刚性传动系统动力学方程［9］为

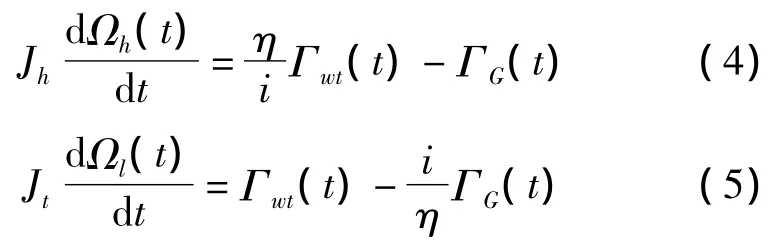
其中:Ωh(t)为发电机转子转速，Ωh(t)=i·Ωl(t);i为齿轮传动变速比;η为齿轮传动效率;ΓG(t)为发电机电磁转矩;Jh为传动系统高速轴端的总转动惯量;Jl为传动系统低速轴端的总转动惯量，并且Jh=η(J1+Jwt)/i2+J2+Jg，Jl=(J1+Jwt)+i2(J2+Jg)/η;J1为齿轮高速端转动惯量;J2为齿轮低速端转动惯量;Jg为发电机转子的转动惯量;Jwt为风轮机转轴的转动惯量。

1.3 双馈感应发电机的数学模型

双馈感应发电机(DFIG)定转子三相绕组对称，并均匀分布在电机圆周内，磁路、电路对称分布，在d-q同步旋转坐标系下数学模型［10］可由以下方程构成:

磁链方程为

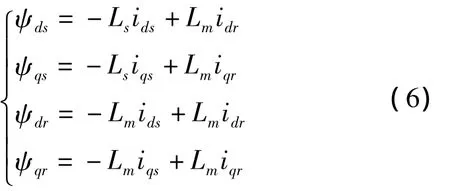
电压方程为

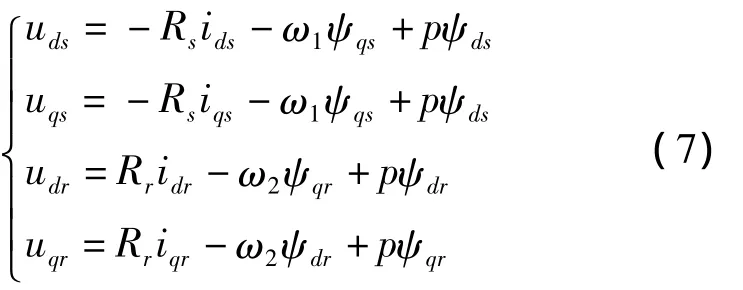
电磁转矩方程为

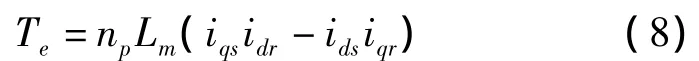
其中:ids，iqs分别为定子 d，q 轴的电流，idr，iqr分别为转子d，q轴的电流;Ls为定子自感，Lr为转子自感，Lm为定转子之间的互感;ψds，ψqs分别为定子 d，q轴磁链，ψdr，ψqr分别为转子 d，q 轴磁链;uds，uqs分别为定子 d，q轴电压，udr，uqr分别为转子 d，q 轴的电压;Te为电磁转矩。

2 模糊PID自适应控制器设计

传统PID控制器只是一组参数进行控制，难以兼顾动态特性与静态特性［11］。因此，这里引入模糊推理，利用知识库，把某些知识与过程状态相结合来决定控制行为［12］。模糊自适应整定PID控制器就是在对象运行时，根据系统的误差信号和误差的微分来在线调整控制器Kp，Ki，Kd3个参数。

如图2结构所示，反馈控制为PID控制，调节反馈控制参数的控制器采用模糊控制。假定Kp，Ki，Kd分别表示PID的比例、积分和微分增益。Kp，Ki，Kd的变化范围分别为［Kpmin，Kpmax］，［Kimin，Kimax］，［Kdmin，Kdmax］。为了方便数据处理，Kp，Ki，Kd通过以下线性变换，归一化变成0和1之间的参数:

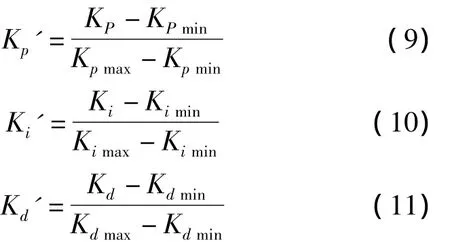
同时对误差e和误差的导数ec也使用归一化，使得ge·e∈［0，1］，gec·ec∈［0，1］。

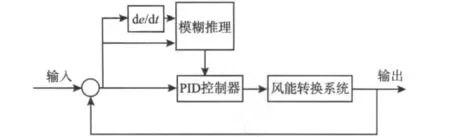
图2 模糊PID控制结构Fig.2 Structure of fuzzy PID control

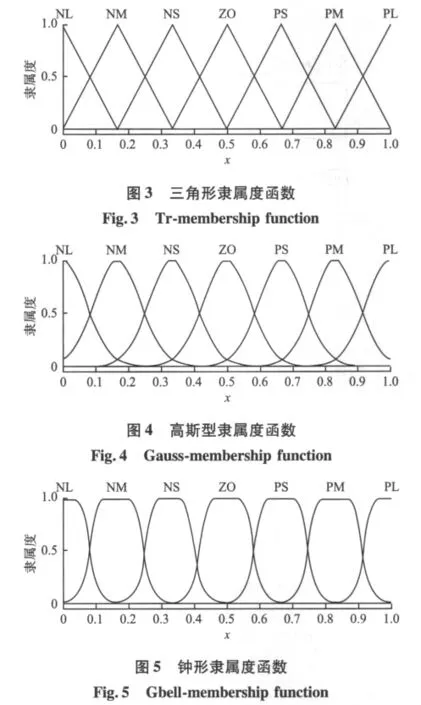
对系统的输入变量 ge·e，gec·ec，在输入论域上定义 7 个模糊子集:{NL，NM，NS，ZO，PS，PM，PL}。输入隶属度函数分别为交叠对称的三角形、高斯型和钟形，如图3，4，5所示。

对系统的输出变量Kp'，Ki'，Kd'，在输出论域上也定义7个模糊子集{NL，NM，NS，ZO，PS，PM，PL}。输出隶属度函数分别为交叠对称的三角形、高斯型和钟形(见图 3，4，5)。

模糊推理是Mamdani型，通过设计人员的技术知识和实际操作经验，采用如下形式的模糊隐含关系:IF e IS A AND ec IS b，THEN u IS C。经过大量仿真研究，最终确定了如表1所示的模糊规则整定表。

3 仿真

利用Matlab/Simulink，在风机的数学模型基础上，搭建了风能最大捕获的风力发电机组模糊PID自适应控制系统仿真模型。模糊推理仿真模型如图6所示。

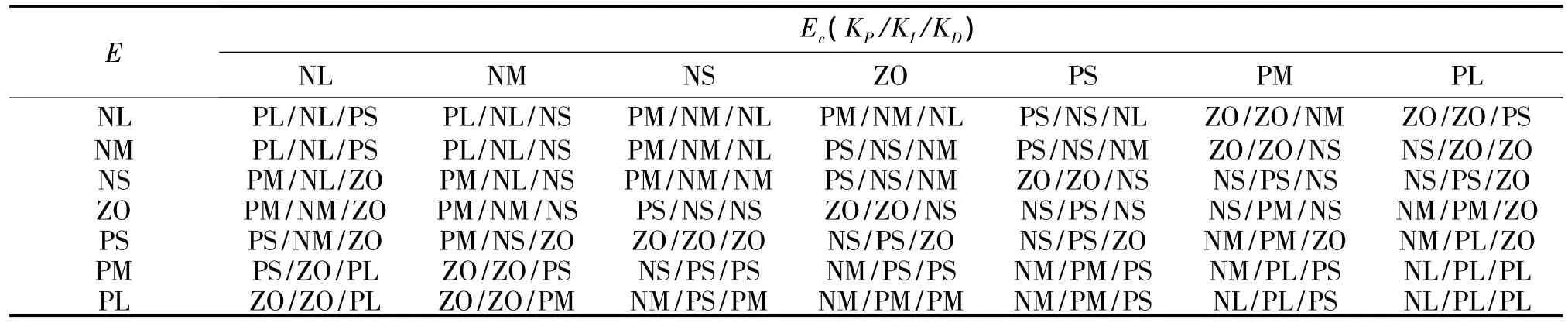
表1 模糊规则整定Tab.1 Rule table of fuzzy control

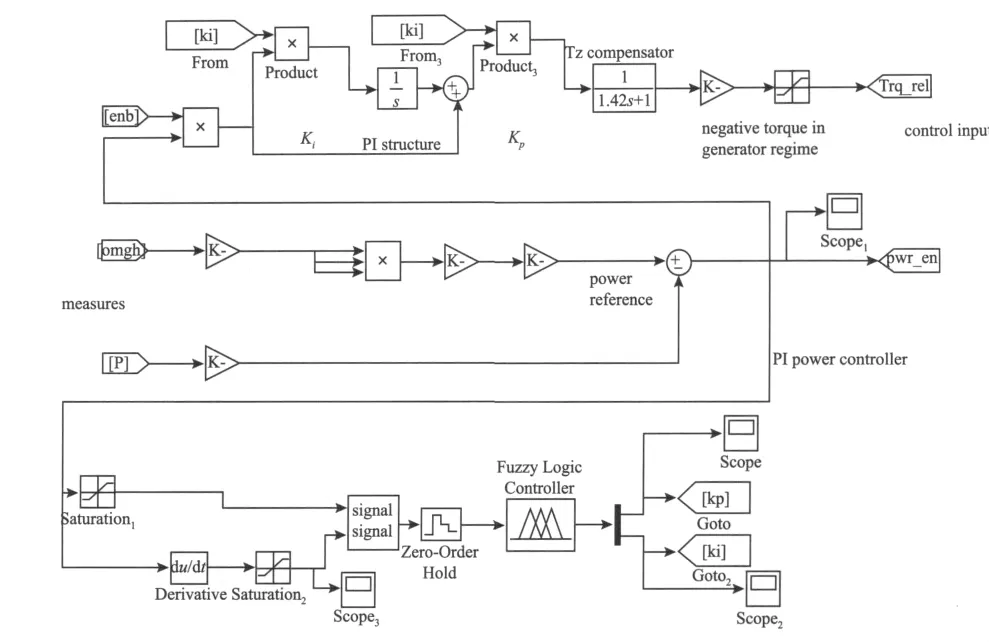
图6 模糊控制的仿真模型Fig.6 Simulation model of fuzzy control

系统仿真参数如表2所示。

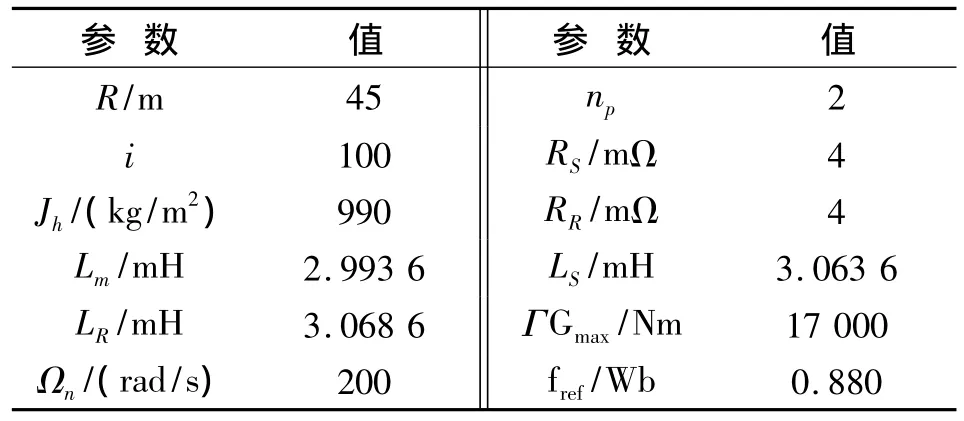
表2 系统仿真参数Tab.2 Simulation parameters

仿真中，一共有3组不同强度的随机风速，平均风速均为7.5 m/s，以测试控制器在各种情况下的表现(其中一组仿真的风速如图7所示)。模糊隶属度函数分别为三角形、高斯型和钟形。

由图7，8，9所示的风速、风能转换系数、叶尖速比仿真波形分析可以知道，基于模糊PID自整定建立的风能转换系统模型，在模糊控制方法下响应快速且平稳，当风速大范围变化时，风能转换系数始终能够保持在最优值0.476附近小范围波动。输出功率的误差减小了很多，能够更好地实现最大功率捕获。

图10 和图11是传统PID控制和模糊自整定PID控制的输出功率误差波形图，图12和图13为PID参数的实时整定图。可以看出，控制器根据风况不断调整PID参数。

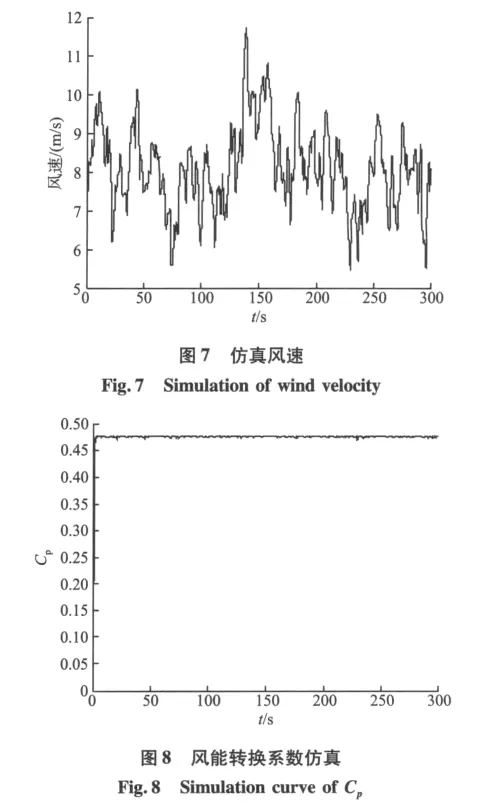
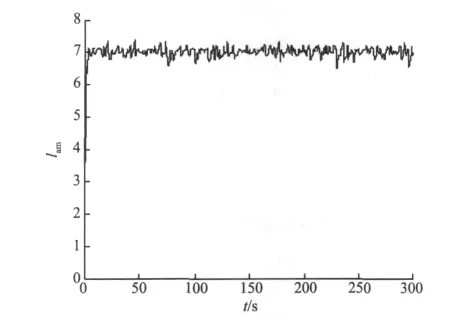
图9 叶尖速比仿真Fig.9 simulation curve of λ

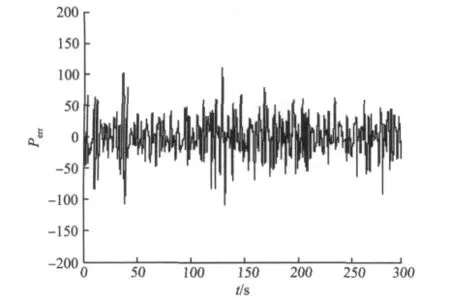
图10 传统PID控制的输出功率误差Fig.10 Perrof conventional PID control

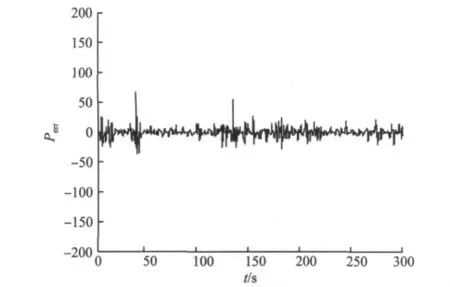
图11 模糊自整定PID控制的输出功率误差Fig.11 Perrof fuzzy self-adaptive control

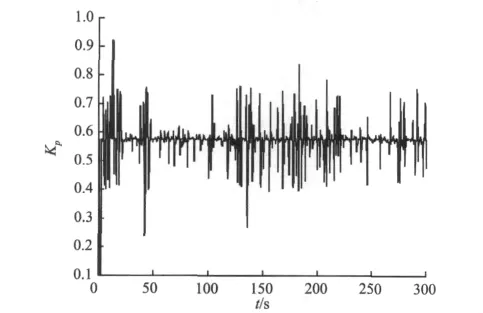
图12 Kp参数整定曲线Fig.12 Simulation curve of Kp

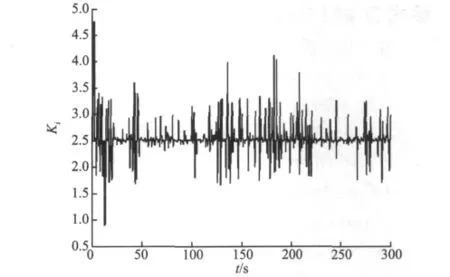
图13 Ki参数整定曲线Fig.13 Simulation curve of Ki

进一步仿真，由表3，4，5的平方偏差积分指标(ISE)和绝对平方偏差积分指标(IAE)表明，基于高斯型隶属度函数的模糊控制有着更好的鲁棒性，在不同的风况下，均能达到最优的性能指标。

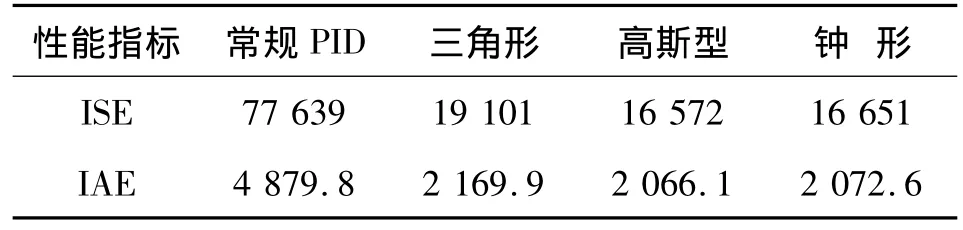
表3 风速1Tab.3 Wind 1

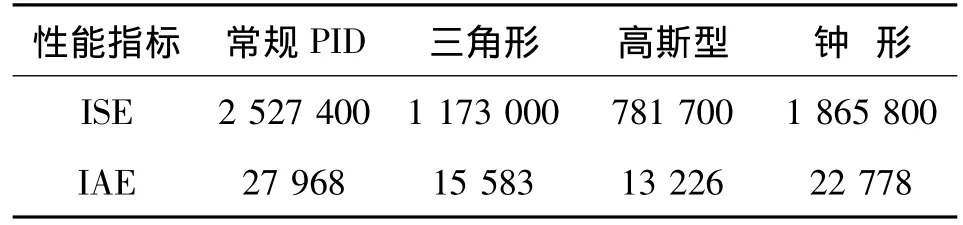
表4 风速2Tab.4 Wind 2

表5 风速3Tab.5 Wind 3

4 结语

基于双馈风能转换系统的数学模型，以最大风能为目标，设计了模糊PID自整定控制器，最后在Matlab/Simulink环境下进行了仿真以验证控制方法的有效性。

仿真结果表明，风速在额定风速以下大范围变化时，模糊PID自整定控制器比传统PID控制更能有效地最大捕获风能，并且在模糊推理中，采用高斯型隶属度函数能达到最优性能指标。

［1］林宗虎.风能及其利用［J］.自然杂志，2008，30(6):309-314.LIN Zong-hu.Wind energy and its utilization［J］.Chinese Journal of Nature，2008，30(6):309-314.(in Chinese)

［2］叶岚.基于继电反馈的PID控制器的参数整定［D］.上海:上海交通大学，2007.

［3］何芝强.PID控制器参数整定方法及其应用研究［D］.杭州:浙江大学，2005.

［4］李国林.PID控制器参数整定技术研究与优化设计［D］.大连:大连理工大学，2010.

［5］林勇刚，李伟，崔宝玲，等.风电机组电液比例变桨距技术研究［J］.太阳能学报，2007，28(6):658-662.LI Yong-gang，LI Wei，CUI Bao-ling，et al.Study on electrohydraulic propotion and pitch-controlled technology of wind turbine［J］.Energiae Solaris Sineca，2007，28(6):658-662.(in Chinese)

［6］Rocha R，Filho L S M.A multivariable H∞ control for wind energy conversion system［C］//IEEE Conference on Control Applications.Hawaii，USA:［s.n.］，2003:468-471.

［7］Lescher F，ZHAO Jing-yun，Borne P.Robust gain scheduling controller for pitch regulated variable speed wind turbine［J］.Studies in Informatics and Control，2005，14(4):299-315.

［8］宋新甫，梁波.基于模糊自适应PID的风力发电系统变桨距控制［J］.电力系统保护与控制，2009，37(16):50-58.SONG Xin-fu，LIANG Bo.Wind power system pitch control based on fuzzy self-learning emendation control theory［J］.Power System Protection and Control，2009，37(16):50-58.(in Chinese)

［9］迟永宁，王伟胜，刘燕华，等.大型风电场对电力系统暂态稳定性的影响［J］.电力系统自动化，2006，20(15):10-14.CHI Yong-ning，WANG Wei-sheng，LIU Yan-hua，et al.Impact of large scale wind farm integration on power system transient stability［J］.Automation of Electric Power Systems，2006，20(15):10-14.(in Chinese)

［10］Inlian Munteanu，Antoneta Iuliana Brarcu，Nicolaos-Antonic Cutululis，et al.Optimal Control of Wind Energy Systems［M］.London:Springer，2008:28-135，150-158.

［11］成虎，刘文丽.风力发电在建筑节能中的应用［J］.东方企业文化，2011(14):289.CHENG Hu，LIU Wen-li.Wind power generation in the application of building energy efficiency［J］.Oriental Enterprise Culture，2011(14):289.(in Chinese)

［12］李英成，纪二云.无功补偿节电技术在电网中的应用研究［J］.科技促进发展:应用版，2011(2):247.LI Ying-cheng，JI Er-yun.The reactive power lompensation power savng technology in the research on the application of power gird［J］.Seience and Technology for Development，2011(2):247.(in Chinese)