一个半离散单调核的Hilbert型不等式
黄臻晓
(湛江师范学院基础教育学院,广东遂溪524300)
若 an,bn≥0,0 <∞,则有以下含有最佳常数因子的离散的Hilbert型不等式[1]:


以上两类不等式是分析学的重要不等式,人们不断推广它们[2-7].对于半离散、齐次核的 Hilbert型不等式,有以下结论[8]:若0 <Σ∞n=1a2n<∞,则有

本文引入2个参数,给出一个新的半离散且单调核的Hilbert型不等式及其等价式.它是式(1)的一个最佳推广.
1 引理
引理1 设A>-1,0<λ≤2,定义权函数和权系数如下:

则有以下不等式:

证明 作变换t=x/n,有


所以式(4)成立.

证明 由带权的Hölder不等式和式(4),有

所以式(5)成立.类似地,由Hölder不等式和式(2)~(4),有


所以式(6)成立.
2 主要结果

这里的常数因子kλ依引理1定义,且kλ,kpλ和kqλ均为最佳值.
证明 由逐项积分定理,I有2种表示.由引理2和条件知,式(7)取严格不等号,所以式(10)成立.由 Hölder不等式,有

由式(10)得式(9).反过来,设式(9)成立.取an=,根据式(9),有


根据式(7)和条件易得 J1<∞.如果 J1=0,则式(10)显然成立;如果J1>0,则式(9)所需的条件都具备,上式取严格不等号,且有

所以式(10)成立,因此式(9)和式(10)等价.
同理,根据条件,式(8)取严格不等号,所以式(11)成立.由 Hölder不等式,有

所以由式(11)可知式(9)成立.反过来,设式(9)成立.取

则由式(9),有

由式(8)和条件可得J2<∞.如果J2=0,则式(11)显然成立;如果J2>0,则式(9)所需的条件都具有,所以上式取严格不等号,且有

所以式(11)成立,从而式(9)和式(11)等价.因此式(9)、(10)与式(11)都等价.

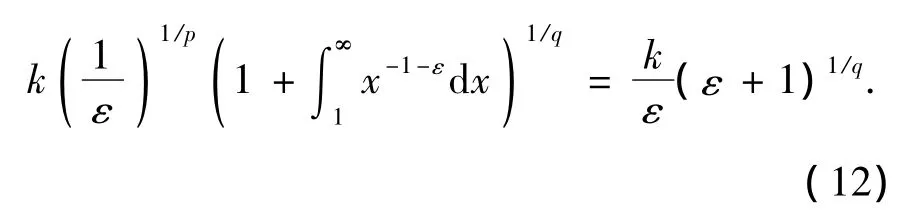
另一方面,由递减性和Fubini定理,又有

由式(12)及式(13),有

再由Fatou引理,有

所以k=kλ是式(9)的最佳值.由等价性易知式(10)和式(11)的常数因子也是最佳值.证毕.
评注 (1)当p=q=2,λ=1,A=0 时,式(9)变为式(1);式(10)、(11)变为与式(1)等价的Hilbert型不等式:

(2)当 p=q=2,λ =1,A=1 时,式(9)变为:
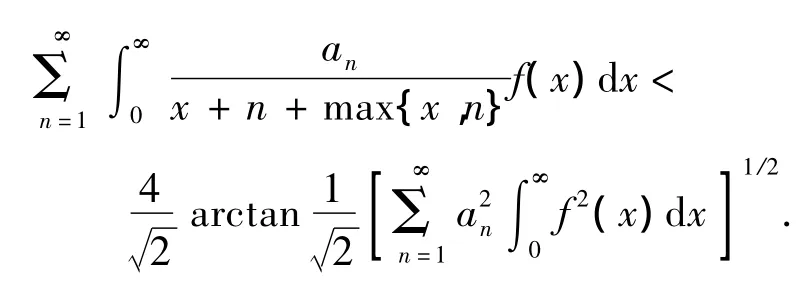
致谢 作者衷心感谢杨必成教授的指导与帮助.
[1]YANG Bicheng.On a relation between Hilbert's inequality and a Hilbert-type inequality[J].Appl Math Lett,2008,21:483-488.
[2]杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009.
[3]黄臻晓,杨必成.一个含参数的零齐次核的Hilbert型积分不等式[J].武汉大学学报:理学版,2011,57(3):241-244.
[4]黄臻晓.一个具有混合核的新的Hilbert型积分不等式[J].数学的实践与认识,2010,40(11):192-197.
[5]黄臻晓.一个-4齐次核的Hilbert型积分不等式[J].华南师范大学学报:自然科学版,2009(2):20-23.
[6]杨必成,陈强.一个半离散且非单调核的Hilbert不等式[J].吉林大学学报:理学版,2012,50(2):167-172.
[7]杨必成.关于一个半离散的Hilbert不等式[J].汕头大学学报:自然科学版,2011,26(4):5-10.
[8]杨必成.一个半离散的Hilbert不等式[J].广东第二师范学院学报,2011,31(3):1-7.

