一种快速的单模式匹配算法
杨子江,聂瑞华,2*
(1.华南师范大学计算机学院,广东广州510631;2.华南师范大学网络中心,广东广州510631)
模式匹配是指在文本串 T=T[0]T[1]…T[n-2]T[n-1]中查找 P=P[0]P[1]…P[m-2]P[m-1].该技术广泛应用于信息检索、数据挖掘、模式识别和入侵检测等领域,而匹配算法的好坏直接影响该系统效率.
模式匹配分为多模式串匹配和单模式串匹配,多模式串匹配算法有AC算法[1]等其他一些改进算法,单模式串匹配的主要算法有BF算法[2]、KMP算法[3]和 BM 算法[4]等.BM 及其改进算法(如 BMH算法[5]、BMHS算法)由于效率较高而被广泛应用.本文首先介绍BM算法和改进算法BMH、BMHS等,分析各种算法的优缺点,在此基础上提出一个新的单模式匹配算法——Y_BMHS.
1 相关算法介绍
假设文本串 T=T[0]T[1]T[2]…T[n-2]T[n-1],长度是 n;模式串 P=P[0]P[1]P[2]…P[m-2]P[m-1],长度是 m;匹配进行到文本串的 j处,现在就BM算法以及改进算法作简单的介绍.
1.1 BM、BMH、BMHS 算法
1977 年,BOYER 和 MOORE[4]提出了 BM 算法.BM算法是先将模式串P与文本串T左对齐,从P的最右端字符往左开始匹配,一直到P中的字符全部匹配成功或者是有不匹配的字符出现时循环结束.算法采用根据2个预先定义的跳跃数组Badchar和Goodsuffix计算出的位移量进行移动.Badchar和Goodsuffix根据已匹配的字符串和未匹配字符的位置进行计算.当文本串字符与模式串字符失配时,根据数组Badchar和Goodsuffix取其中较大者为shift的值,将模式P往右移shift个字符,继续进行下一轮匹配,匹配成功则直接输出.
BM算法考虑全面,包括了右移时的所有情况,但它使用了2个数组,预处理花费太多时间,程序实现复杂,并且Badchar被选为shift的值出现的概率远比Goodsuffix的大,而在匹配过程中两者都用,进行了大量不必要的比较,降低了匹配速度.
HORSPOOL[5]于 1980 年提出了 BMH 算法,该算法将匹配字符串与计算右移量独立,即在计算右移量时不关心匹配位置和匹配情况.当发生失配时,通过与模式串末端对应的文本串位置的字符计算右移量.
BMH算法较BM算法有更好的性能,它只使用了Badchar数组,简化了预处理过程,并且省去比较shift值的过程,实践也证明BMH性能更优.它仅仅通过一个字符计算右移量,增加了很多不必要的比较和移动.
SUNDAY[6]于1990年在BMH算法的基础上又提出了改进的BMHS算法.其主要改进思想是:在计算Badchar函数时,利用模式串末端对应的文本串位置的下一字符决定右移量.当比较进行到文本串 j位置,失配发生在 T[i+j]=b 与 P[i]=a 处,只使用T[j+m]=c决定右移量.当发生失配时,若c未出现在P中,则直接右移m+1位,否则与P中从右往左第一次出现的相同字符对齐,继续进行下一轮匹配.
该算法中,当下一个字符T[j+m]未出现在模式中时,它的右移量比BMH算法的右移量大,BMHS算法右移m+1位,BMH算法只能右移Badchar[j+m-1]位置,最多移动m位,故BMHS算法通常比BMH算法快.而当T[j+m-1]不在模式中出现而T[j+m]出现时,BMHS算法就比BMH算法慢.
1.2 N_BMHS、IBMHS、Im_Sunday 算法
N_BMHS算法[7]是在 BMHS算法的基础上,引入一个数组S标记模式串中字符出现的次数,并在匹配过程上采用两端向中间交替匹配的顺序,一旦失配,利用已匹配位置和辅助数组S的信息进行移动,有效减少了移动和比较次数.
IBMHS算法[8]综合了BMH和BMHS算法的特点,并利用频度函数使得最大位移m+1出现频率提高,从而降低匹配时间.算法的主要过程是:在第j轮匹配中,分别计算出采用BMH和BMHS算法启发规则得到的窗口移动值qsBc[T[j+m-1]]-1和qsBc[T[j+m]]并进行比较.若后者大于前者,直接移动qsBc[T[j+m]],否则根据字符出现的频次进行(m+1)或 qsBc[T[j+m-1]]-1的移位.
Im_Sunday算法[9]使用与模式串最右端对应的文本串字符的下一个字符 S[next]和 S[nnext].S[nnext]是 S[next]后面 m 长度位置的字符,即nnext=next+plen.当 S[next]字符在模式串中出现时,匹配方法与BMHS算法相同.当S[next]字符未在模式串中出现时,判断S[nnext]字符是否出现在模式串中.若出现,将模式串中最右端第一个出现的字符与S[nnext]对齐,否则将整个模式串移动到 S[nnext]的右侧.
1.3 算法分析
在以上算法中,BM算法是最全面和最复杂的算法,它充分考虑了所有的可能性,但预处理花费太多时间,并且在选择shift值和匹配上进行了太多次不必要的比较.BMH较BM算法有改进,它只采用坏字符的移动规则,并且将字符匹配和计算位移量独立,加快了匹配速度.BMHS是在BMH的基础上进行的改进,其最大位移是m+1,BMH则是m,通常情况下BMHS要比BMH算法的速度更快.IBMHS算法综合了前两者的优点,并利用字符出现次数提高了最大位移m+1的频率.N_BMHS利用已匹配位置和频度数组,能有效减少移动和比较次数.Im_Sunday算法在匹配过程中利用了 S[next]和S[nnext]字符,在一定程度上减少了比较.
然而,上述匹配算法仅仅利用模式串末端字符对应的文本串的一个字符或下一字符的信息进行跳跃,从而进行了很多次不必要的比较和跳跃,且其跳跃距离和最大跳跃距离出现概率均偏小,造成匹配速度变慢.
模式匹配存在2个基本定理:任何文本串匹配算法在最坏情况下必须检查文本串中至少n-m+1个字符;任何模式匹配算法至少检查 n/m个字符[10].因此,没有一个算法的计算复杂度比BM算法及其改进算法还要优越,但是我们可以通过增加偏移量,减少匹配次数,获得更好的性能.
2 改进算法——Y_BMHS算法
根据概率论的理论,2个字符出现在文本串中的概率远小于一个字符出现的概率,所以通过创建一个二维数组,既可以增大最大位移,又可以提高最大位移出现的概率,而有一些模式串的特点是:有大量重复的前缀和后缀如in、ex、ly和组合字符串如ea、se、at等,Y_BMHS算法正是基于这样的想法,结合模式串本身的特点,在BMHS算法的基础上,采用与模式串末端对应的文本串位置(i-1)的下2个字符 T[i]和 T[i+2](非连续字符)和模式串首字母的唯一性来计算位移量,非连续字符在一定程度下可以加快匹配速度.该算法将T[i]和T[i+2]作为一个子串,在模式串中出现时,则右移模式串使得子串与文本串从右往左出现的相同子串对齐,否则根据不同情况进行右移处理,最大位移为m+3,其中m是模式串的长度.下面以算法的预处理阶段和匹配阶段做详细阐述.
2.1 预处理阶段
因为使用2个字符的子串决定右移量,所以我们采用辅助的二维数组来表示位移量.预处理阶段主要是对该位移量数组进行初始化.假设m是模式串P的长度,i是匹配过程中模式串末端对应的文本串的下一位置,则子串为 T[i]T[i+2].对数组进行如下初始化:
第一步,将数组初始值置为m+3;
第二步,考虑如下几种特殊情况:
(1)当 T[i]=P[m-1]时,文本串可能匹配.此时,模式串右移1位,置值为1,如图1A.
(2)当 T[i]=P[m-2]时,文本串可能匹配.此时,模式串右移2位,置值为2,如图1B.
(3)当 T[i+2]=P[1]时,文本串可能匹配.此时,模式串右移m+1位,置值为m+1,如图1C.
(4)当 T[i+2]=P[0]时,文本串可能匹配.此时,模式串右移m+2位,置值为m+2,如图1D.
第三步,当子串在模式串P中出现时,将其与P中从右到左第一次出现的子串对齐.

图1 4种可能的匹配情况Figure 1 Four possiblematch situations
2.2 匹配阶段
在匹配阶段中,研究了Im_Sunday算法并对其进行了改进.根据概率论的理论,发生失配时,循环判断此时的位移量.若位移量为m+3,则模式串向右移动m+3,并继续循环,否则退出循环进行下一轮匹配.考虑一种特殊情况,如图2示.
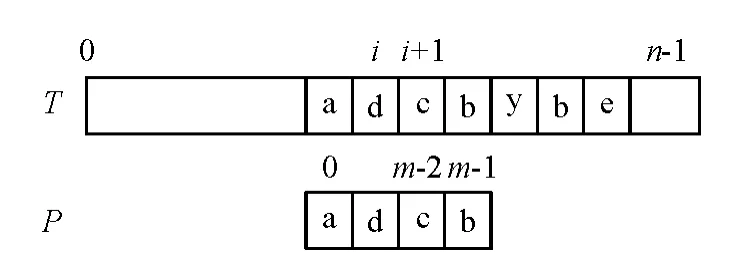
图2 右移后匹配Figure 2 Match after rightmove
此时,右移量还是m+3,但明显已经匹配了,所以在循环中须加入判断.
综上所述,实际的匹配流程如图3示.
根据上述算法的描述,以T=“Manyarygycnobgtifintromtnology”,P=“nology”为例进行搜索.开始匹配时,把模式串与文本串自左边对齐.具体匹配过程如表1所示.
(1)第1 次:T[6]=‘y’=P[m-1],模式串右移1位.
(2)第2次:T[7]=‘g’=P[m-2],模式串右移2位.
(3)第3次:T[10]=‘n’=P[0],模式串右移m+1位.
(4)第4次:T[18]=‘n’=P[0],模式串右移m+2位.
(5)第5 次:T[24]T[26]=“nl”,P 中存在该子串,根据跳跃表移动6位,找到字符串,匹配结束.
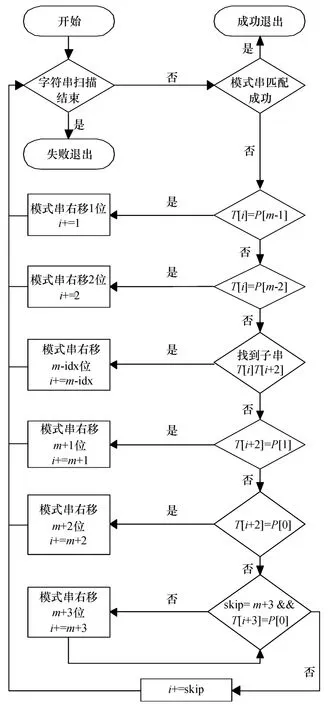
图3 Y_BMHS算法的匹配流程Figure 3 Match process of Y_BMHS

表1 Y_BMHS算法匹配过程Table 1 Thematch process of Y_BMHS algorithm
2.3 算法分析
从Y_BMHS算法的匹配过程可以看出,它是一种典型的以空间换取时间的算法.BMH、BMHS算法在比较时每次只取一个字符进行比较,当发生失配时,以P中某位置对应的文本串的字符T[i]的位移量作为P的移动距离.这种情况下,只有当T[i]不在P中出现时,模式串才能获得最大移动距离.从概率上来说,2个连续字符出现在模式串中的概率远远低于一个字符出现的概率,模式串的特性又使得间隔的两字符在模式串中出现的概率一般低于2个连续字符出现的概率,Y_BMHS算法以间隔2个字符计算偏移量作为P的移动距离,模式串获得最大移动距离m+3的概率也大得多,并且在匹配阶段通过位移量的判断,最大限度地提高了移动距离,这样显然可以获得更高的匹配速度.
3 算法性能测试
本实验使用的计算机硬件平台为Intel(R)CoreTM i5-2430 M处理器,4 G内存,软件平台为Windows7 64位操作系统,MicroSoft Visual Studio 2010集成开发环境.现采用随机函数产生一段随机长度为500~1 000的文本串和随机长度为5~10的模式串,分别用 BM、BMH、BMHS、IBMHS、Im_Sunday、Y_BMHS算法进行匹配测试,测试程序与算法均用C语言编写,用主程序调用这6种匹配算法,匹配算法中均插入CPU内部时间戳进行高精度计时,同时统计每种算法一次匹配中平均位移量等数据.实验结果见表2.

表2 实验结果比较Table 2 Experimental results
通过上述实验测试可知,Y_BMHS算法在单模式匹配算法中,平均位移量更大,最大位移出现的概率更高,能够快速提高匹配速度,对模式串匹配有更明显的加速效果.
4 结束语
Y_BMHS算法采用辅助的二维数组记录位移量,通过对模式串末端字符对应的文本串位置的下2个间隔字符的比较,并且在匹配阶段尽可能地使模式串右移,使得模式串以最大位移量m+3进行右移的几率变得更大.通过对算法的分析和实验证明,该算法能够有效地增加模式串右移量,大幅度提高匹配速度,降低匹配时间.
[1]AHO A V,CORASICK M J.Efficient string matching:An aid to bibliographic search[J].Commun ACM,1975,18(6):333-340.
[2]CHARRAS C,LECROQ T.Exact string matching algo-rithms[EB/OL].(1997-01-14)[2012-04-03].http://www.r-igm.univ-mlv.fr/lecroq/string.
[3]KNUTH D E,MORRIS JH,PRATT V R.Fast pattern in strings[J].SIAM JComput,1977,6(2):323-350.
[4]BOYER R S,MOORE JS.A fast string searching algorithm[J].Commun ACM,1977,20(10):762-772.
[5]HORSPOOL N R.Practical fast searching in strings[J].Software Practice and Experience,1980,10(6):501-506.
[6]SUNDAY D M.A very fast substring search algorithm[J].Comm ACM,1990,33(8):132-142.
[7]单懿慧,蒋玉明,田诗源.面向入侵检测的改进BMHS模式匹配算法[J].计算机工程,2009,35(24):170-173.
[8]岳成刚.基于 Snort平台的网络入侵检测系统研究[D].合肥:合肥工业大学,2009.
[9]武旭东.Snort入侵检测系统研究与应用[D].吉林:吉林大学,2011.
[10]李雪莹,刘宝旭.字符串匹配技术研究[J].计算机工程,2004,30(22):24-26.

