分形结构团聚体在流场中分散混合的数值模拟*

麻向军 邱忠财 陶成文

(华南理工大学聚合物新型成型装备国家工程研究中心，广东广州510640)

分散混合在材料加工中起着重要作用，尤其是颗粒团聚体在聚合物熔体中的混合与复合过程．分散混合的目的是在流体拖曳力作用下，打破分散相颗粒团聚体内的物理键合，使其发生剥蚀或破碎，从而获得更小的碎片或者颗粒［1］．预测和控制分散混合过程对设计和操作混合设备进而提高最终制品性能有重要意义，许多研究者从理论和实验两方面对分散混合现象进行了研究．Feke等［2］提出了一种用于确定团聚体在剪切流场中破碎的概率模型;Horwatt等［3］将处于剪切流场的非均质团聚体视为一个内聚力作用下的连续体，确定了团聚体破碎时的临界流体拖曳力;Scurati等［4］考虑了团聚体尺寸、流体黏度和剪切速率对分散过程的影响，开发了一种用于预测分形结构团聚体在稳态和非稳态剪切流场中分散的剥蚀动力学模型，并与实验结果进行了对比．

随着计算机技术的发展，数值模拟广泛用于研究分散混合现象，常用的模型有连续介质模型和离散介质模型．由于颗粒团聚体是典型的离散体，力学特征“散”而“动”(“散”是指颗粒性质、尺寸和形貌的分散性，“动”是指颗粒运动的瞬时性和非线性)，不满足连续模型的小变形和位移协调的假设，因此，应采用离散介质模型研究分散混合过程［5］．目前，离散介质模型中应用最广泛的是Cundall［6］提出的离散单元法(DEM)，其基本原理是将离散介质视为独立的块体或颗粒单元的集合，单元之间的相互作用力可根据力和位移的关系确定，单元的运动由牛顿运动定律确定，运动过程中，单元之间可接触也可分开，允许单元发生很大的平动和转动，可以求解一些离散介质的力学行为，如堆积、流动和分离［7-9］．近年来，国外一些学者将DEM应用于研究分散混合现象，显示出这一方法的优越性［10-12］，但是对于分形结构团聚体分散混合的研究较少．文中在经典离散元理论模型中引入范德华力和流体拖曳力，编制了二维离散元程序DEMix2D，并对二维情况下由均质的纳米级球形颗粒组成的具有分形结构的团聚体在纯剪切、纯拉伸和剪切-拉伸混合流场中的分散混合行为进行数值模拟．

1 数值模型

1．1 颗粒运动控制方程

由于分散混合过程非常复杂，必须做一些简化和假设:①忽略颗粒重力和布朗运动;②颗粒密度和流体密度相近，忽略浮力的作用;③流体处于层流状态，且只考虑流体对颗粒的作用力，不考虑颗粒对流体的作用力，并且认为颗粒在流体中的任意分布不会影响流场分布;④流场无边界．满足以上假设后，团聚体在分散过程中，每个颗粒受到的力包括颗粒间的接触力、范德华力以及流体拖曳力．颗粒受到这些力作用后的运动可由牛顿第二定律求得:

式中，m、I、vi和ωi分别为颗粒i的质量、转动惯量、速度和角速度，Fi和Mi分别为颗粒i受到的合力和合力矩．Fi和Mi可表示成:

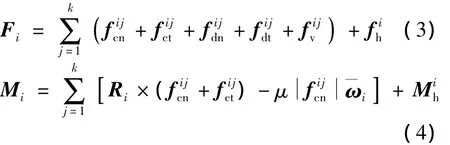
1．2 接触模型

颗粒间的接触力和阻尼力可以根据力与位移的关系(即接触模型)求得．文中采用Cundall的线性粘弹性模型［10］，即颗粒间可以理解为线性弹簧、线性粘壶和滑片相连接的形式，如图1所示．

线性粘弹性接触模型中，接触力和阻尼力表示为

式中:kn和kt分别为弹簧的法向刚度和切向刚度，kn= RE，kt=kn/10，其中R为颗粒半径，E为颗粒的弹性模量［10］;dn和 dt分别为法向和切向阻尼系数分别为法向和切向相对位移，vn，ij和 vt，ij分别为法向和切向相对速度．同时，和还须满足库伦-摩尔摩擦准则［13］．

1．3 范德华力

根据Hamaker理论，两个半径相同的球形颗粒i、j之间的范德华力fijv为

式中，A和h分别表示Hamaker常数和两颗粒间隔距离，nij为单位向量．

式中，xi和xj为颗粒i和j的位置矢量．

1．4 流体拖曳力

流体拖曳力的计算是模拟颗粒团聚体分散行为的关键，目前普遍采用的方法是根据斯托克斯定律求解拖曳力和力矩．颗粒在剪切流场中受到的流体拖曳力如图2所示．

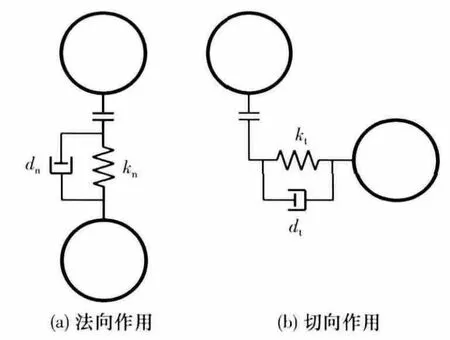
图1 颗粒间的接触模型Fig．1 Contact model between particles

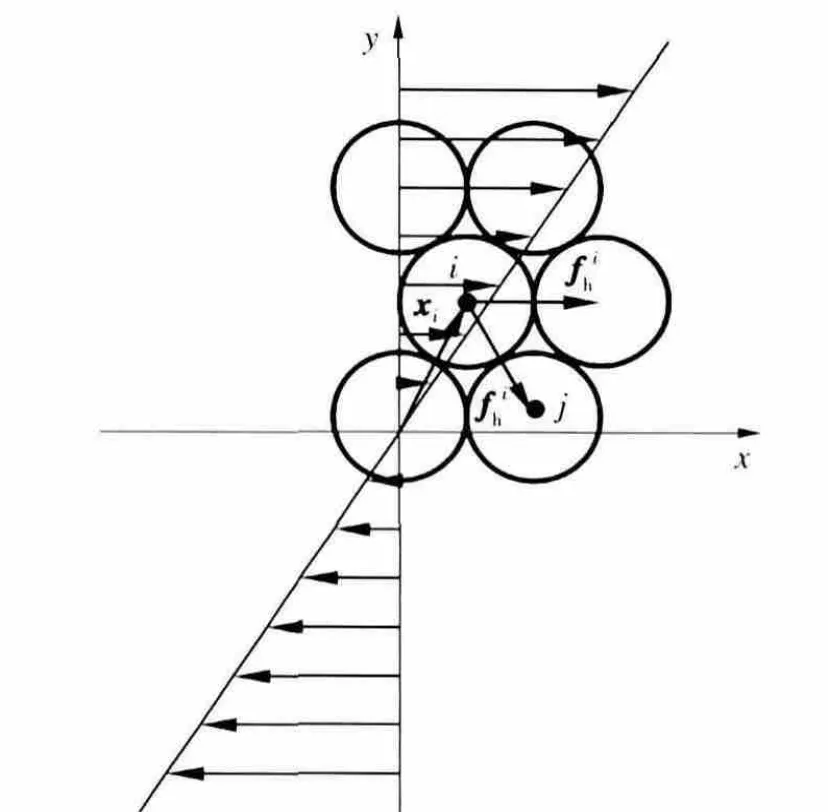
图2 颗粒在剪切流场中的受力示意图Fig．2 Schematic diagram of forces on particles in shear flow field

根据斯托克斯定律，单个颗粒处于流场时受到的拖曳力和力矩分别为

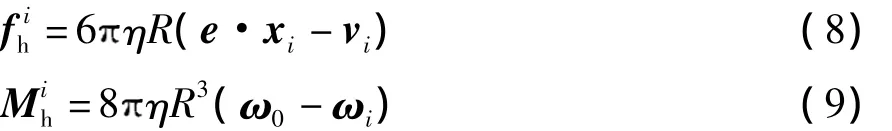
式中:η表示流体黏度;e和ω0分别表示流场的速度梯度张量和涡度矢量，与流场类型有关．

对于二维纯剪切流场:

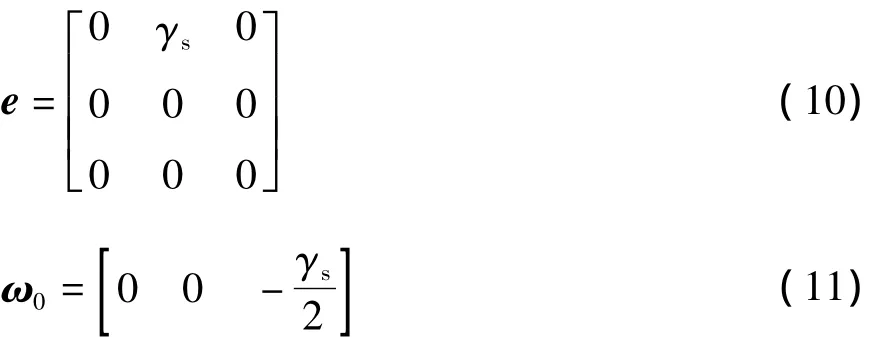
式中，γs为剪切速率．

对于单轴拉伸流场:

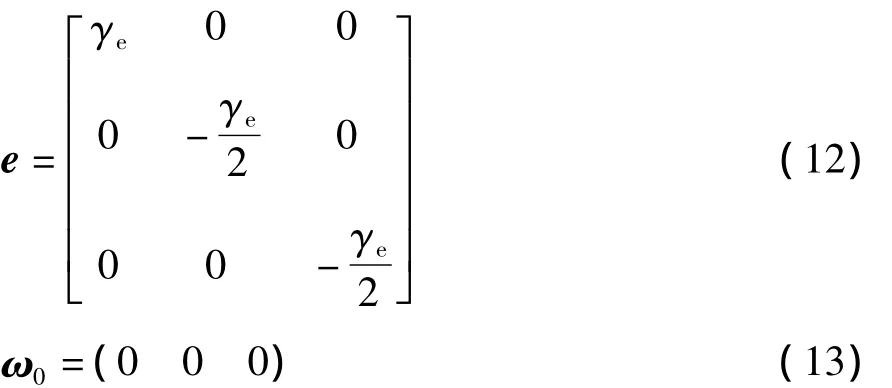
式中，γe为拉伸速率．

对于剪切-拉伸混合流场，e和ω0可认为是两种流场的叠加［15］:

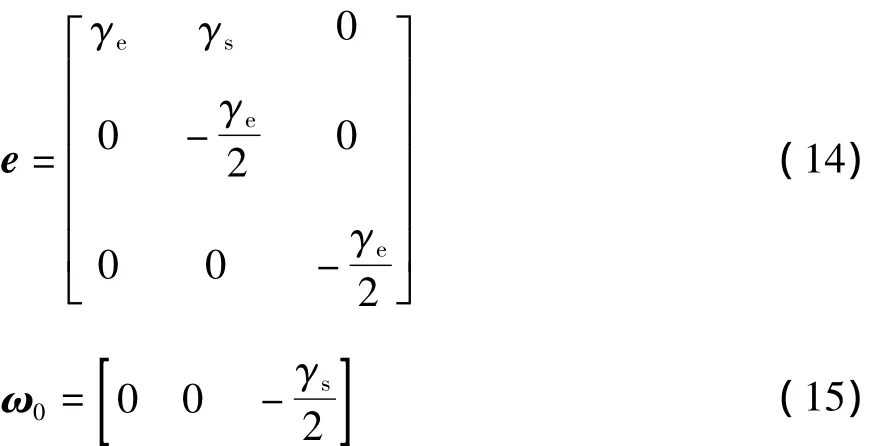
两种流场叠加时形变速率张量第二不变量I2相等，因此，γs和 γe必须满足 γs=

团聚体中的颗粒与单个颗粒受到的流体拖曳力不同．团聚体中的颗粒由于受到周围颗粒的影响，计算团聚体中每个颗粒受到的流体拖曳力和力矩时需要引入一个有效因子ζ以反映周围颗粒的影响．团聚体中颗粒半径一致时，一个颗粒周围最多有6个接触颗粒，此时，该颗粒被接触颗粒包围，可认为它没有受到流体的作用，即ζ=0;当这个颗粒周围有5个接触颗粒时，则ζ=1/6;依此类推，当这个颗粒没有接触颗粒时，ζ=1．

1．5 运动方程求解

采用基于软球模型的离散元方法，对运动方程采用欧拉格式求解［16］．任一时刻t，根据团聚体中任一颗粒i在空间的位置及其周围颗粒的位置，可由接触模型、范德华力模型和流体拖曳力模型计算出该颗粒受到的接触力、阻尼力、范德华力和流体拖曳力之和Fi(xi(t))，然后根据运动方程可计算得到t+Δt时刻颗粒i的位置和速度，即

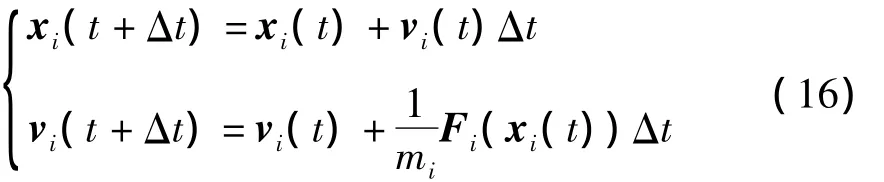
当初始条件给定时，就可以由前一时刻颗粒i的位置和速度确定下一时刻的位置和速度，进而确定团聚体在流场作用下的演变过程．

由于对运动方程采用欧拉格式求解，因此是条件稳定的，时间步长必须小于临界值才能保证算法稳定．文中采用简谐振动法确定临界时间步长，即

式中，C为时间步长安全系数，k为弹簧的刚度．

2 模拟条件及参数

2．1 颗粒团聚体结构生成

在已有的研究中，通常以致密堆积的团聚体为对象，而实际的团聚体结构非常复杂，通常具有分形结构．在二维情况下，以团聚体中心的颗粒为圆心，任意长度r为半径的圆内含有的颗粒数为N(r)，若N(r)与r满足以下关系:

则认为团聚体满足分形结构，其中z为分形维数，它反映了复杂形体占有空间的有效性．根据这个规定，生成团聚体的方法为:首先在流场中心生成一个初始颗粒1，然后生成任意一个与颗粒1相切的颗粒2，再生成第3个颗粒，该颗粒与之前生成的至少1个颗粒相切且不与其他颗粒交叉，同时满足式(18)，如此重复下去直到生成所需要的颗粒数．图3为采用上述方法生成的团聚体，颗粒数为130，z为1．8．

2．2 计算参数

模拟过程中，流场强度必须足够大才能打破团聚体的物理键合使其分散．定义流场强度:

图3 团聚体结构Fig．3 Structure of agglomerates

选取不同流场强度下的剪切、拉伸和剪切-拉伸混合流场进行团聚体分散行为的模拟计算，流场强度分别为460、820和1200Pa．模拟计算中的其他参数如表1所示．

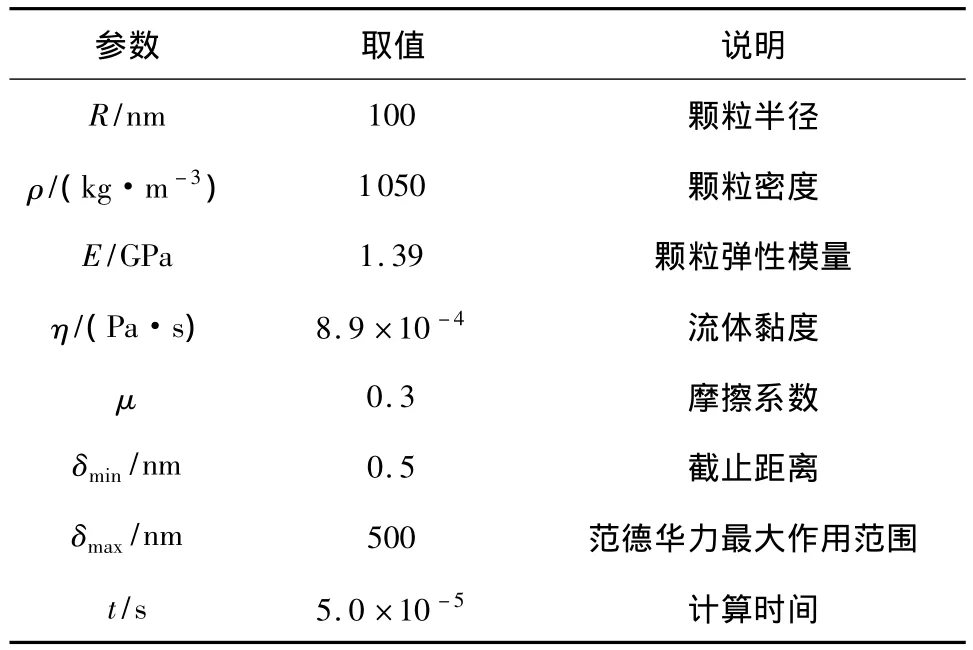
表1 模拟计算中的参数Table 1 Parameters used in simulation

3 模拟结果与分析

3．1 流场形式对分散过程的影响

流场强度为820Pa时，模拟计算得到的团聚体在剪切流场、拉伸流场、剪切-拉伸混合流场中的分散过程如图4所示．

由图4可见，3种形式的流场中，团聚体均先发生相应的变形，然后再分散成碎片或者颗粒，团聚体在分散过程中存在剥蚀和破裂两种分散方式，在团聚体内部连接较弱的位置更容易发生破裂，破裂后的碎片中颗粒排列比初始团聚体中颗粒排列更为致密．随着分散的进行，颗粒速度增加，颗粒与流体之间的相对速度减小导致流体拖曳力减小，直至与范德华力达到平衡时不再分散．

图4 流场强度为820 Pa时团聚体在不同流场中的分散过程Fig．4 Time evolution of dispersion of agglomerates in different flow fields at a flow stress of 820Pa

比较团聚体在不同流场中的分散行为，可以看出，团聚体在拉伸流场中可以获得较小的碎片，即团聚体更容易分散，混合流场次之，而剪切流场的分散能力最低．这是由于团聚体在剪切流场中受到剪切应力作用后，团聚体分散的同时还存在转动，消耗了部分流体传递给团聚体的能量;此外，团聚体在分散过程中颗粒的排列更为紧密，团聚体的内聚力增加，使其分散变得更为困难．而拉伸流场中团聚体没有转动，流体传递的能量全部用于团聚体的分散，而且团聚体在分散过程中颗粒排列较为疏松，颗粒间的内聚力较弱，因而团聚体最容易分散．混合流场中的剪切分量亦会使部分能量用于团聚体的转动，而且分散过程中颗粒的排列也没有剪切流场中紧密．因此，拉伸流场的分散效率最高，混合流场次之，剪切流场的分散效率最低．

3．2 团聚体分散动力学

为了定量分析流场的分散性能，以分散得到的碎片的加权平均颗粒数〈w〉表征分散度．采用〈w〉随时间的变化曲线来分析分散混合的动力学过程．定义加权平均颗粒数为

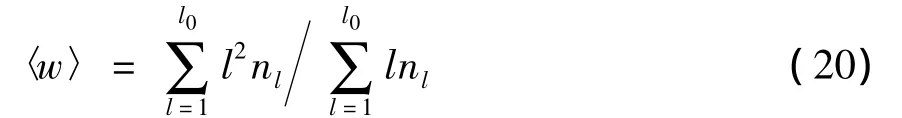
式中，nl为包含l个颗粒的碎片数，l0为团聚体初始时刻的颗粒数．

流场强度为820Pa时，团聚体在剪切、拉伸和剪切-拉伸混合流场中的分散度随时间的变化如图5所示．

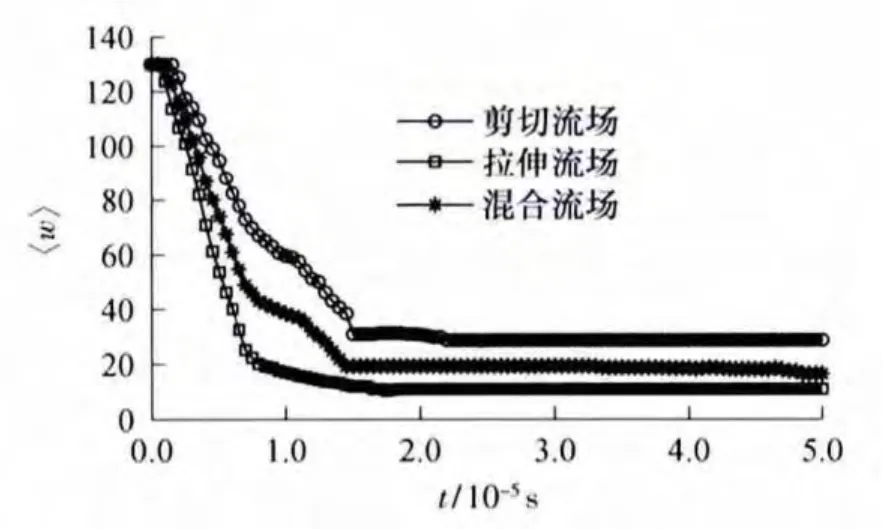
图5 流场强度为820Pa时团聚体的分散度随时间的变化Fig．5 Dispersity of agglomerates changing with time at a flow stress of 820Pa

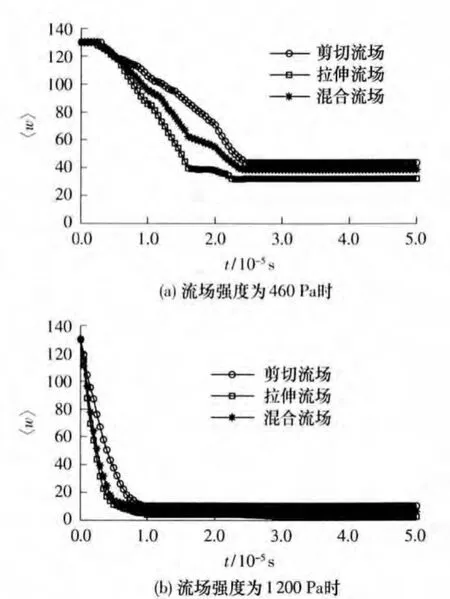
图6 不同流场强度时在不同流场下团聚体的分散度随时间的变化Fig．6 Dispersity of agglomerates changing with time in different flow fields with different flow stresses

由图5可见:刚开始时团聚体只有变形而没有分散，经过一定时间后才开始分散;拉伸流场中团聚体最先开始分散，团聚体达到稳定的分散度所用时间最短，分散度也最小;而剪切流场中团聚体从变形到开始分散所用时间最长，达到稳定的分散度所用时间最长，分散度最大．

流场强度为460和1200 Pa时，团聚体在剪切、拉伸和混合流场中的分散度随时间的变化如图6所示．

观察图6发现，其变化趋势和图5一致．比较图5和6可以看出，对于形式相同的流场，随着流场强度的增加，由于流场作用于团聚体的能量增加，团聚体从变形到开始分散所用时间缩短，达到稳定的分散度所用时间缩短，分散度减小．

4 结论

通过对二维情况下均质纳米级球形颗粒组成的具有分形结构的团聚体在纯剪切、纯拉伸和剪切-拉伸混合流场中的分散混合行为进行数值模拟，得出以下结论:

(1)分形结构团聚体在流场中先发生变形然后再分散，分散过程中存在剥蚀和破裂两种分散方式，分散后的碎片比初始团聚体更加致密．

(2)流场强度相同时，团聚体在拉伸流场中的分散效率最高，碎片平均尺寸最小;在剪切流场中的分散效率最低，碎片平均尺寸最大．

(3)在相同形式的流场中，随着流场强度增加，团聚体的分散效率提高，碎片平均尺寸减小．

［1］塔德莫尔Z，高戈斯C G．聚合物加工原理［M］．任冬云，译．北京:化学工业出版社，1990:239-241．

［2］Feke D L，Manas-Zloczower I．Rupture of inhomogeneous spherical clusters by simple flows［J］．Chemical Engineering Science，1991，46(8):2153-2156．

［3］Horwatt S W，Manas-Zloczower I，Feke D L．Dispersion behavior of heterogeneous agglomerates at supercritical stresses［J］．Polymer Engineering and Science，1992，47(8):1849-1855．

［4］Scurati A，Feke D L，Manas-Zloczower I．Analysis of the kinetics of agglomerate erosion in simple shear flows［J］．Chemical EngineeringScience，2005，60(23):6564-6573．

［5］孙其诚，王光谦．颗粒流动力学及其离散模型评述［J］．力学进展，2008，38(1):87-100．Sun Qi-cheng，Wang Guang-qian．Review on granular flow dynamics and its discrete element method ［J］．Advances in Mechanics，2008，38(1):87-100．

［6］Cundall P A．A computer model for simulating progressive，large-scale movements in blocky rock systems［C］∥Proceedings of the Symposium of the International Society of Rock Mechanics．Rotterdam:Balkama A A，1971:8-12．

［7］徐泳，孙其诚，张凌，等．颗粒离散元法研究进展［J］．力学进展，2003，33(2):251-260．Xu Yong，Sun Qi-cheng，Zhang Ling，et al．Advances in discrete element methods for particulate materials［J］．Advances in Mechanics，2003，33(2):251-260．

［8］Zhu H P，Zhou Z Y，Yang R Y，et al．Discrete particle simulation of particulate systems:theoretical developments［J］．Chemical Engineering Science，2007，62(23):3378-3396．

［9］Zhu H P，Zhou Z Y，Yang R Y，et al．Discrete particle simulation of particulate systems:a review of major applications and findings［J］．Chemical Engineering Science，2008，63(23):5728-5770．

［10］Higashitani K，Iimura K．Two-dimensional simulation of the breakup process of aggregates in shear and elongational flows［J］．Journal of Colloid and Interface Science，1998，204(2):320-327．

［11］Eggersdorfer M L，Kadau D，Herrmann H J，et al．Fragmentation and restructuring of soft-agglomerates under shear［J］．Journal of Colloid and Interface Science，2010，342(2):261-268．

［12］Hosseini M S，Nazockdast H，Dabi B．Numerical simulation of aggregate dispersion in different flow fields using discrete element method ［J］．Applied Polymer Science，2010，115(6):3303-3310．

［13］Cundall P A，Strack O D L．A discrete numerical model for granular assemblies ［J］．Geotechnique，1979，29(1):47-65．

［14］Yang R Y，Zou R P，Yu A B．Computer simulation of the packing of fine particles［J］．Physical Review E，2000，62(3):3900-3908．

［15］林师沛，赵洪，刘芳．塑料加工流变学及其应用［M］．北京:国防工业出版社，2008:58-62．

［16］孙其诚，王光谦．颗粒物质力学导论［M］．北京:科学出版社，2009:63-70．