一种基于粒子群优化的Snake模型的指纹分割方法

汪庆

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

1 引言

指纹作为一个重要的人体生物特征已被广泛用于社会个人信息安全保护等领域，对指纹图像准确的分割，获取真实有效的指纹区域，能够减少特征提取的处理时间、提高指纹识别的正确率，对于提高整个指纹系统的效率具有重要意义。

目前，许多学者对指纹图像分割方法进行了研究，通常采用指纹图像块特征进行分割，已经取得了不少成果，但各种算法往往也存在各自的不足之处。Snake模型①Kass M,Witkin A,Terzopoulous D.Snakes:Active Contour Models，International Journal of Computer Vision,1988,1(4):321-331.是由Kass等于1987年提出的一种基于能量最小化的轮廓检测算法，该模型是以一组相对靠近图像目标的点作为初始轮廓，通过能量函数极小化，使得轮廓产生弹性形变，将轮廓形状锁定在目标特征附近，达到分割的目的。

本文在对指纹图像分割处理过程中，针对传统Snake模型存在的一些不足，提出了一种改进的Snake模型指纹分割方法。该方法解决了Snake模型初始轮廓点的自动确定问题，并通过粒子群优化算法（PSO）改进了指纹凹陷区域无法捕获问题。

2 传统Snake模型

传统Snake模型首先根据经验将初始轮廓手工分布于靠近目标图像边缘，然后根据图像的连续性、平滑性和外力的共同作用定义一个能量函数，该能量使得边缘向能量函数减少的区域移动，当能量函数趋于稳定时，形成最终的轮廓曲线。该模型的能量函数为：

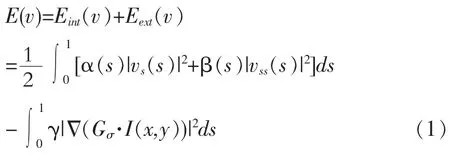
其中，S 表示弧长，Eint（v）为内部能量，防止曲线拉伸或者弯曲，α（s），β（s）分别为一阶导数和二阶导数的加权系数，其中一阶导数项是曲线的斜率，用于控制曲线的连续性，二阶导数项是曲线的曲率，用于控制曲线轮廓的弹性程度。Eext（v）为外部能量，用于引导曲线向图像轮廓的边缘移动为梯度算子，Gσ·I（x,y）表示图像与特征密度为σ的Gaussan平滑滤波器卷积。

但是，传统Snake模型也存在不足①李培华，张田文：《主动轮廓线模型（蛇模型）综述》，《软件学报》2000年第6期，第751-757页。：1.初始轮廓点位置需要相对地接近目标，否则可能无法获得正确的目标图像。这需要通过一定的方法尽可能将初始轮廓点放在目标图像附近。2.凹陷区域不能够捕获。不少学者对该模型进行了研究，并取得了一定的成果。李涛等人②李涛，于明，兰娜：《一种自动初始化轮廓的改进蛇模型算法》，《河北工业大学学报》2006年第1期，第58-61页。提出了一种利用重心发出射线来获取初始轮廓点的方法。XU等人③Xu C,Prince J L.Snakes,Shapes,and Gradient Vector Flow，IEEE Transaction on Image Processing,1998,7(3)pp.359-369.提出了一种能够检测出凹陷区域的GVF Snake模型，该模型利用扩散方程获得图像域梯度向量场作为新的外力。

针对Snake模型的这两个缺点，本文做出了一些改进：1.利用基于凸包算法的方法自动获取模型初始轮廓；2.对改进了的Snake模型，利用PSO算法解决指纹图像凹陷区域不能收敛的问题。

3 改进的Snake模型方法

3.1 初始轮廓确定

通常对Snake模型初始轮廓的确定是采用手工获取，但是手工的方法无法实现图像分割的自动处理。针对指纹图像的特殊性，本文提出了一种基于凸包算法的初始轮廓获取方法，该方法无需人工干预，能够自动获取初始化轮廓。初始点个数由初始点间隔step控制。

获取初始轮廓算法如下：

Step1：利用canny算子获取指纹纹路的边界；

Step2：对Step1中获取的边界进行凸包计算，获取一组能使最小多边形包含所有的点集；

Step3：对Step2中获取的凸包点集进行排序并均匀间隔取点，得到最终的初始轮廓。

3.2 Snake模型改进

3.2.1 PSO算法

PSO算法④倪庆剑，邢汉承，张志政等：《粒子群优化算法研究进展》，《模式识别与人工智能》2007年第3期，第349-357页。模拟鸟群飞行觅食的行为，通过鸟群中个体之间的协作使群体达到最优，是一种群智能算法。基本的PSO算法流程如下：

Step1：初始化粒子群位置xi和初始速度vi；

Step2：对每个粒子计算适应度函数值ffit；

Step3：根据适应度函数更新选出局部最优值pbesti和全局最优值gbesti；

Step4：由公式(2)更新粒子速度和公式(3)更新下一代粒子的速度和位置；

Step5：若满足达到阈值跳转或迭代次数最大值，跳转step 6，否则跳转step2；

Step6：算法结束，输出结果。

粒子速度更新：

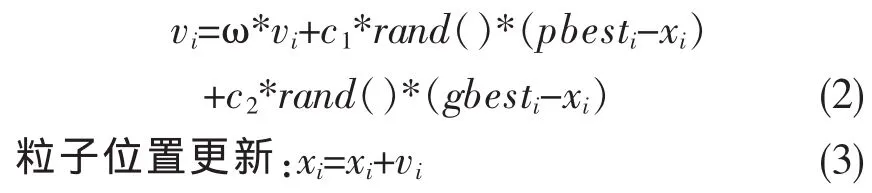
其中，ω 为惯性因子，c1，c2为学习因子，rand（）是0和1之间服从均匀分布的随机数。

3.2.2 适应度函数选取

对于PSO算法中的适应度函数的选取，本文使用了优化后的Snake模型：

为了进行仿真实验，需要将曲线S描述成一组控制点，能量最小化过程就是通过这组控制点迭代完成的。为了计算控制点pi（x,y）周围的能量，将Snake模型积分形式离散化为差分形式：

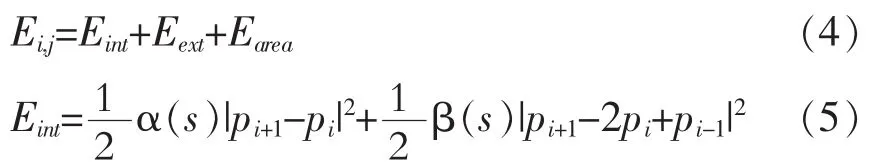
//内部能量控制轮廓的连续性和弹性

//外部能量控制曲线向指纹图像边缘移动

此外，外力方面添加一个面积力使得曲线更加接近区域真实指纹区域：

//搜索到凹陷区域位置时，Sarea越小，能量越趋于极小化。

最终的适应度函数表达形式为：

3.2.3 基于粒子群优化的Snake模型的分割算法

传统Snake模型应对指纹图像进行分割时，对含有凹陷区域的指纹不能很好地收敛。PSO算法是一种进化学习算法。通过Snake模型能量构造出的改进的含有面积因素的适应度函数ffit对粒子进行约束，经过不断地迭代更新每个粒子的速度和位置，获得粒子的全局最优值，得到优化的控制点。经过对每个初始轮廓点进行优化后的PSO算法，获得优化后的极值轮廓点，最终完成对含有凹陷区域的指纹图准确分割。

算法流程：

Step1：初始化粒子群算法参数：惯性因子ω，加速因子c1、c2，最大迭代次数MaxIter，群体数目PopSize；

Step2：设定粒子搜索范围边界，防止溢出；

Step3：初始化粒子初始位置pi和初始速度vi；

Step4：根据公式（8）计算粒子适应度值 ffit；

Step5：记录粒子的局部最优位置pbesti，记录最佳适应度值ffitbest；

Step6：根据粒子的pbesti，更新全局最优位置gbesti；

Step7：更新粒子速度 vi、更新粒子位置 gbesti、更新粒子适应度ffit；

Step8：若满足迭代次数最大值，转入Step9，否则跳转Step 7；

Step9：若所有初始轮廓点运算完毕，转入Step10，否则跳转Step1；

Step10：获得全部轮廓点的最优值，完成指纹分割。

本文PSO算法参数选取：惯性因子ω＝0.8，加速因子c1=c2=2，最大迭代次数MaxIter=50，群体数目 PopSize＝20。

4 实验结果分析

本文的实验环境为：T2400 1.83GHz CPU 2G内存；XP操作系统；使用Matlab7.0实现。

通过对指纹图像进行仿真实验后，从图1和图2可以看出实验对比结果。在每组图中：（a）表示原始指纹图像；（b）表示使用凸包算法后获取的指纹轮廓线；（c）表示均匀化后初始轮廓点的分布；（d）表示传统Snake模型方法分割的结果；（e）表示使用PSO优化的Snake模型分割的结果。本文将Snake模型能量的参数赋值为： 图 1：α＝0.05，β＝0.05，γ＝30，δ＝0.05，step=5；图 2： α＝0.05，β＝0.05，γ＝50，δ＝0.05，step=10。

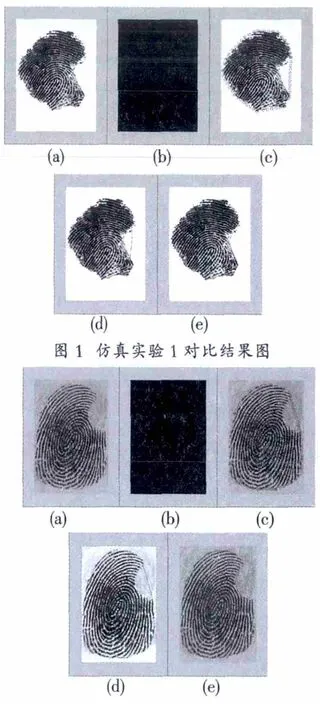
图2 仿真实验2对比结果图

图1-d和图2-d是传统Snake模型方法分割的结果，该算法不能准确收敛于凹陷指纹边界区域；图1-e和图2-e是使用PSO优化后的Snake算法运行结果。从实验结果可以看出，优化后的Snake算法能够准确地收敛到指纹的凹陷边界处，从而实现了对目标的准确分割。

结束语

本文针对传统Snake模型在指纹图像初始轮廓点的自动确定和凹陷区域的准确收敛这两个问题做出了一定的改进。首先通过凸包算法解决了初始轮廓点自动提取问题，然后利用具有全局优化能力的PSO算法改进了凹陷区域收敛性。实验结果表明，该算法能够自动提取指纹图像的初始轮廓，并且能够准确地收敛到指纹凹陷区域，完成指纹图像的准确分割。