管理级软件能力成熟度的模糊评价研究

周伟良

(1.安徽经济管理学院，安徽 合肥 230059；2.合肥工业大学 管理学院，安徽 合肥 230009)

一、引 言

随着软件质量管理研究的不断深入，对于软件产品的质量控制逐渐转移到对软件过程的质量控制和软件组织的软件能力控制上来。如何提升软件组织的软件能力受到愈加广泛的关注。美国卡内基—梅隆大学软件工程研究所研发的软件能力成熟度模型(Capability Maturity Model，简称CMM)以及在此基础上形成的软件能力成熟度模型集成成为评估软件组织软件能力成熟度的重要工具。CMMI模型主要是对软件组织设计开发软件的能力进行评估，而并非针对软件或软件项目本身［1-2］，因此，CMMI并没有定义实施软件过程度量中收集并分析软件过程数据的具体方法，由此可见，CMMI的软件能力成熟度评估还是以定性评价为主的。

在软件过程质量度量研究方面，宿为民、朱三元提出从过程建模的角度考虑支持过程度量，并给出一个支持过程度量的软件过程建模GQM-D(Goal Question Metric-Data)方法［3］。北京航空航天大学软件工程研究所的李健等则重点分析了对软件过程的度量和不同过程成熟度层次对度量的需求［4］。上海大学的潘秋菱等结合自主开发的软件过程工程环境Softev，提出了在软件开发中进行度量的一组指标，这些指标都在Softev中得以实现［5］。在基于CMMI的软件成熟度度量方面，主要的研究工作是基于CMMI模型研究软件风险的定量分析方法，或是着重阐述了评价模型中数据收集、分析的方法，以及结合生命周期法或GQM方法构建软件过程的性能模型［6-9］。

综上所述，目前软件过程度量并未很好地引入CMMI基本理论和方法，同时CMMI的应用研究又主要以定性研究为主，缺少以CMMI为基础的度量研究，此外，目前的软件质量度量研究不能够充分地关注企业尤其是中国小型软件企业实施CMMI的成本和困难。由于软件企业无论是获取CMMI认证还是认证后持续使用CMMI的评估方案，都会面临实施时间长、成本高等因素，国内的大多数软件组织并不会持续采用CMMI中的方法，监控和改进企业软件过程的质量，这使得企业在不同软件项目的质量管理上依然存在差别。

因此，从软件过程质量管理的角度看，在不同的软件项目上，以及项目的不同阶段，以CMMI方法为基础，设计低成本、高效率的软件组织软件能力成熟度的度量方法，对提升软件组织软件开发能力，保障软件产品质量，将是必要和有效的。

鉴于目前参与CMMI评估的国内企业通过CMMI第2级(管理级)认证占多数，通过CMMI第3级(定义级)及以上认证的企业相对较少。本文从CMMI模型第2级(管理级)出发，并依托KW公司的软件开发项目，重点从CMMI的管理级梳理评估软件组织软件能力成熟度的主要指标，构建软件能力成熟度的评价指标体系。同时依据CMMI过程域、目标及其具体实践，设计相应的基于隶属度的管理级软件能力成熟度量化评价模型，为软件企业在项目过程中更加有效地采用CMMI评估软件组织的软件能力提供支持，降低评估成本，以期对CMMI的具体应用及软件组织软件能力评估提供支持。

二、指标体系构建

(一)初始指标项的建立和数据采集

CMMI模型第2级(管理级)共涉及7个过程域，15个特定目标，1个通用目标［10］，分别用SG1～SG15表示特定目标，用GG表示通用目标，具体信息定义如下：

依托KW公司的软件项目以及开发资源，本文针对上述16个指标项采集了涉及3个软件项目，5组质量监控的专家评价数据，并以{0,1,2,3,4,5,6,7,8,9}为标度，分别采集软件开发不同阶段各指标项的评价结果值。同时，以{1,1.5,2,2.5,3,3.5，…，9.5,10}为标度，采集软件产品的整体评估结果V，得到表1、表2的数据，其中定义Pij为第i组第j个项目的采集数据。

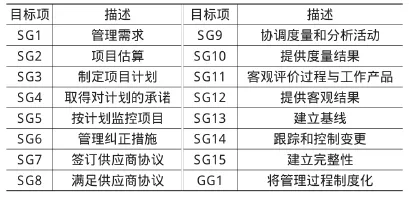
表1 管理级软件能力成熟度相应目标项

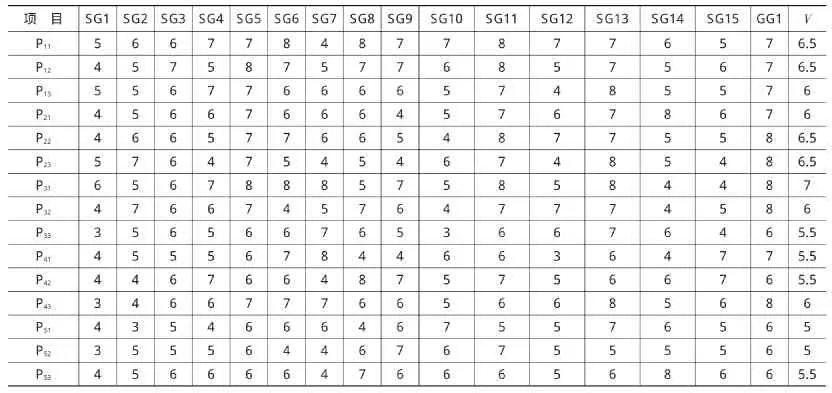
表2 具体软件项目的评估数据

(二)指标项的筛选

以减少度量复杂度，降低循环实施度量所需成本为目标，需要对指标项进行必要的筛选。指标项筛选的主要任务在于，在管理级的16个指标中筛选出对软件成熟度影响更大且更具独立性的指标项用于后续的软件成熟度度量。筛选的主要思路是，首先通过问卷调查剔除部分非关键指标项；其次，通过相关性分析，剔除部分存在直接相关关系的指标项，保证筛选出的指标项符合相应的独立性要求；第三，根据实际意义，V与各指标项存在强正相关关系或弱正相关关系，因此对初步形成的指标子集，结合V值，实施线性回归分析，剔除由于调查数据缺陷造成的不符合正相关要求的指标项，形成新的指标子集，并再次实施线性回归分析，直至形成的指标子集各指标项与V均符合正相关的要求，并以最终形成的指标子集作为管理级软件能力成熟度评估的评价指标。

指标筛选步骤如下：

(1)通过问卷调查，剔除部分选择率小于5%的指标项：SG4，SG6，SG8(略去具体数据和过程)，由此筛选得到指标子集 A={SG1，SG2，SG3,SG5，SG7，SG9，SG10，SG11，SG12，SG13，SG14，SG15，GG1}。

(2)变量间的相关性分析，利用SPSS进行变量间相关性分析的数据如表3所示。

表3 SPSS的相关性分析数据

表3中，指标项SG10，SG14，SG15与V的Pearson Correlation值分别为-0.126，-0.293，-0.329，其余指标项的Pearson Correlation值均大于0，从实际意义的角度看，所有指标项与最终评价值的相关关系应该为强正相关关系或弱正相关关系，因此，从相关关系上看,除SG10，SG14，SG15的指标项是不符合实际意义的，剔除SG10，SG14，SG15三个指标项，得到指标子集B={SG1，SG2，SG3，SG4，SG5，SG6，SG7，SG8，SG9，SG11，SG12，SG13， GG1}。

(3)对指标子集A和B取交集，得到指标子集C=A∩B={SG1，SG2，SG3，SG5，SG7，SG9，SG11，SG12，SG13，GG1}。以表2数据为基础，设V为因变量，以C中指标项为自变量，设:V=b0+b1×SG1+b2×SG2+b3×SG3+b4×SG5+b5×SG7+b6×SG9+b7×SG11+b8×SG12+b9×SG13+b10×GG1，根据实际意义，V与各指标项存在强正相关关系或弱正相关关系，因此b1，b2，…，b10均应大于0。应用Enter(强制引入)回归方法，进行多元线性回归分析，其Model Summary部分的R2=0.967，ANOVA部分的P=0.015＜0.05，可以认为因变量V与自变量{SG1，SG2，SG3， SG5，SG7，SG9，SG11，SG12，SG13，GG1}有显著的线性回归关系。同时，Coefficients部分显示，SG7，SG9的B值(非标准回归系数)均小于0，与实际意义不符合，因此剔除SG7，SG9得到D={SG1，SG2，SG3，SG5，SG11，SG12，SG13，GG1}。

(4)同理，剔除SG12得到E={SG1，SG2，SG3，SG5，SG11，SG13，GG1}。

(5)根据线性回归分析得到的Model Summary部分的R2=0.964，ANOVA部分的P=0.000＜0.05，可以认为因变量V与自变量E={SG1，SG2，SG3， SG5， SG11，SG13，GG1}有显著的线性回归关系。

因此，将E={SG1，SG2，SG3， SG5， SG11，SG13，GG1}作为软件组织管理级软件能力成熟度评估的评价指标。

(三)指标权重的确定

多目标多因素决策中，需要对不同决策者提供的多个判断矩阵进行集结，以形成一个更加合理的解决方案，本文采用Hadamard凸组合［11］进行相应的判断矩阵集结。

为了简化问题描述，本文在问卷调查中也采集了专家判断矩阵，在符合一致性前提的专家判断矩阵中，按照一致性比率CR从小到大的次序，取前5位专家判断矩阵如下：

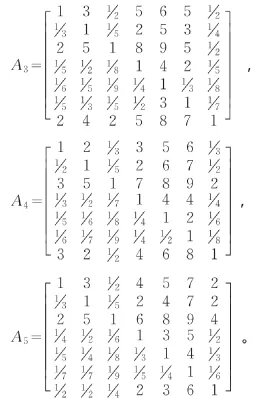
上述5个判断矩阵一致性比率分别为：(0.041,0.045,0.047,0.048,0.050)T。

为了更好地进行判断矩阵权重的计算，首先给出相关定义。文献［11］给出了Hadamard凸组合的概念，即：若A1，A2，…，Am是同一个问题的m个判断矩阵，若存在：,:使得

对于C=A⊕B，有cij=aij+bij；对于C=A·B，有cij=aij·bij。

为便于讨论，本文取λL=(0.2,0.2,0.2,0.2,0.2)。

利用方根法得到其CR=0.032＜0.1。因此W结果符合一致性要求。

(四)成熟度能力的模糊评价

1.参量说明

定义1：给定论域S=［0，9］，表示对于管理级软件过程能力成熟度的度量值域。

定义2：设A为S上一模糊子集合，分别表示管理级软件能力的五个子等级：I级、II级、III级、IV级和V级；I级为管理级中软件能力成熟度最高，V级为管理级中软件能力成熟度最低；

定义3：u(x)表示x相对于A中各级别的隶属度；u(x)∈［0，1］，其中x∈S；x表示相应指标项的评价值；

定义4：W=(w1,w2,…,wt,)为管理级中软件能力成熟度各评价指标的相对重要程度即权重，t表示指标项个数；

假设1：x＜1,u(x)=0,x≥9,u(x)=1；

假设2：管理级中五个能力子等级对应的隶属度要求分别为：

2.隶属函数定义

典型的隶属度函数在图形分布上主要包括正态分布、Γ分布，戒上分布、戒下分布以及半梯形分布等［12-13］，考虑软件过程能力评估的特性，本文选取半梯形分布作为确定隶属度函数的基础，并以假设1作为约束条件，定义如下隶属度函数。

因此，对于多项目的信息采集而言，可以定义其相应的综合隶属度函数：

其中，u(xij)表示第i个指标项在第j个项目中相对于管理级的隶属度。

同时可以得到，在具有多项指标体系的管理级软件能力成熟度评价中，各指标项反映的软件能力隶属于管理级的特征向量为：U=(u1,u2,…,u5)。

3.评价模型的构建与实施

特征向量U反映软件项目样本对管理级软件能力成熟度的隶属度，结合各指标项的权重，可建立相应的模糊评价模型：

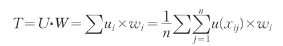
结合表1的评价数据，抽取出相应指标项对应的具体数据，应用算式(1)和(2)，可以得到：

对矩阵U′每列应用算术平均可得：

参照假设2，则通过对3个项目、5个专家、7个指标项的分析，该软件组织隶属于管理级的隶属度约为0.688，即认为该软件组织在管理级五个子成熟度级别中处于第IV级。

三、结束语

CMMI作为对软件企业进行软件开发能力评估的重要模型，其方法在软件项目的各个阶段都具有十分重要的借鉴意义。针对国内软件企业现状，本文以CMMI的主要理论和方法为基础，以回归分析为手段筛选出管理级软件能力成熟度的关键指标项，以hadamard凸组合为方法确定指标权重，以模糊综合评价的基本理论为依据设计新的管理级软件能力成熟度模糊评价模型，帮助软件组织可以在不同的软件项目以及项目的不同阶段循环实施相应的模糊评价方案，以此实现对软件项目质量更加有效的量化控制，同时促进企业能够更加广泛和深入地应用CMMI的基本理论和方法，提高企业软件质量管理的能力，这对于CMMI的量化研究和国内软件企业循环实施CMMI方法都将会起到十分积极的作用。

［1］Carnegie Mellon University，Software Engineering Institute.CMMIFrequently Asked Question［R］.CMU/SEI，2001.

［2］CMU SEI.Concept of Operations for the Capability Maturity Model Integration［EB/OL］.［2012-11-25］.http://www.sei.emu.edu.

［3］宿为民，朱三元.支持过程度量的软件过程建模方法的研究［J］.软件学报，1999，10(8)：843-849.

［4］李健，金茂忠.软件过程度量技术的研究［J］.计算机工程与应用，2001(5)：86-89.

［5］潘秋菱，刘宗田，贾亮，等.软件过程技术及环境［J］.研究电子学报，2001(11)：1-3.

［6］金兰.CMMI软件风险定量研究［J］.价值工程，2010(14)：162-163.

［7］王慧，周伯生，罗文劼.基于CMMI的软件过程性能模型［J］.计算机工程与设计，2009(1)：110-112.

［8］贺赟.CMMI基于CMMI的软件过程度量［J］.电脑知识与技术，2008，4(7)：1647-1649.

［9］田秀彦.基于CMMI模型进行过程改进［J］.科技信息，2008(14)：32-33.

［10］CMMI Product Team.CMMl for Development Version 1.2［EB/OL］.［2012-11-20］.http://www.sei.cmu.edu.

［11］刘心报，杨善林.判断矩阵的Hadamard凸组合［J］.系统工程理论与实践，2000，20(4)：83-85.

［12］万中，梁文冬，卢宗娟.模糊数的隶属度区间分布函数［J］.重庆理工大学学报(自然科学版)，2011(1)：107-112.

［13］刘开第，庞彦军，栗文国.多指标决策中隶属度转换算法及其应用［J］.自动化学报，2009(3)：315-319.