引力模型下的新旧城区空间相互作用研究——以南京为例

何 颖

根据国务院发展2研1究中心发展战略和区域经济研究部的一项课题研究报告， 世纪，随着全球化、科技进步背景下的生产模式、消费模式、治理模式和产业结构等方面的重大变化，人类经济和社会活动的空间布局随之也已经发生了重大变化，进入了城市为主的时代[1]。城市化或城镇化时代的到来，必然会对城市发展中的城市形态、功能定位、空间布局等一系列问题作系统的优化考虑。然而，从快速发展的中国城市化进程看，它又是在中国的基本国情、政府的政策导向等宏观背景下进行的，其突出特点之一，是老城区的改造与新城区的构建几乎同时进行。因此，如何协调“新”与“旧”、怎样统筹“拆”与“建”的矛盾，进而构建起新旧城区的良性互动关系，就成为当前推进城市化进程中亟待解决的一个突出问题。在这方面，龙青云借助物理学中万有引力定律来建立城市间的人口往来数量模型，并提出模型在城市规划中的应用，为城市规划提供了有益参考[2]。李江苏等以昆明市为例，利用其构建的新的引力模型表达式测算了昆明市区与各郊区县间的空间相互作用力，提出促进城郊区互动的建议[3]。关于江苏城市之间的空间相互作用的研究1也3取得了初步进展，孟德友等采用引力、潜力和场强模型对 个地级市的空间相互作用进行测度，对影响江苏省城市空间相互作用强度的因素进行了深入分析[4]。本文以南京市为例，利用引力模型对新旧城区间的空间相互作用进行进一步探讨。

一、引力模型

当代城市化进程的实践表明，城市发展不单是城市发展空间的拓展，更主要还在于能够对供给城市可持续发展的各种资源的竞争、占有和配置。对于当下中国城市化进程中的旧城改造和新城区的构建来说，建构新旧城区之间互通有无的良性互动关系，是推进城市化的必然选择。从经济地理学中的“空间相互作用理论”[5]看，这一良性互动关系的建构，实际上就是要在新旧城区之间，实现信息、资金、技术、劳动力等经济要素之间的顺畅传输，不断增强彼此之间的关联性和参与性，也就是深入增强二者之间的相互吸引力和作用力。因此，判断新旧城区之间的相互作用如何，可以通过建构一种引力模型来深入考察二者之间的互动关系和互动程度。

作为在空间经济和社会科学研究中被广泛、持续运用的空间相互作用模型——引力模型(Gravity Model)，它是Tinbergen和Poyhonen对阻抗函数模型的内核进行改进，并以牛顿万有引力公式为基础，后在经济学领域不断拓展、深化，提出的一个既完整又易于应用的经济学模型。本文则将该模型用于衡量区域科学中的经典主题——两个区域间空间相互作用力大小，其公式通常可以表达为：

在该式中:Iij为i地与j地两者之间的空间相互作用力；Mi、Mj分别是i地和j地的质量；dij为i地与j地两者之间的距离；b是常数[6]。该引力模型表示，两地之间的相互作用力与两地的质量乘积成正比，与两地之间的距离成反比。其实，在该模型中，通常以PiPj、GiGj或来衡量两地的质量M，因而，两地之间的引力计算公式通常也可以表示为:

在(2)、(3)、(4)式中，PiPj代表i与j两地人口规模之积，GiGj代表i和j两地GDP之积，PiGi和PjGj分别表示i和j两地的人口与GDP之积。(4)式虽然在考量空间相互作用时同时关注了人口因子与国民生产总值的作用，但若仅采用这两项指标，必然无法顾及区域质量测度的全面性，至于对区域间的空间相互作用力如何只能粗略地估算，也会使模型的精准度大打折扣。

实际上，区域综合质量评价的重要性在经济学的实际运用中已被广泛关注。建立科学、合理的区域质量评价指标体系，为区域综合质量评价提供了一种新的思考角度，即用区域综合质量指数K来代替某单一指标衡定的区域质量M。对此，业内专家对d的重要性也持有不同的认识和理解，认为将d的内涵狭窄化地界定为两个城市之间的空间距离，难免会有失偏颇，两地间的空间相互作用不是简单地使用距离的概念就能真正体现的。在当今市场经济条件下，尤其应该注意到，距离已经不再是单纯的空间距离，面对一个具体化的经济主体——城市，在理解时显然应杂糅进更多的非空间因素，所以把距离诠释为一个组合成本似乎更能展现其时代特点，即

(5)式中，dij为i与j两地之间的距离；s代表i与j两地之间的第k种运输方式；代表i与j两地之间第s种运输方式的权重；代表i与j两地之间第s种运输方式的货币成本；代表i与j两地之间第s种运输方式的时间成本。

对距离指数b的确认，是基本引力模型中另外一个同样重要的问题，我们虽然在理论上认为，b应等于1或2(即取平方)，但实际研究过程则显示，b值可以在0.5～3.0间上下浮动，这是因为不同的货物，对距离的敏感性也不同，所以2，不同的可运输性会影响到b的取值[7]，在本例中，b的取值为 。综上所述，将引力模型表达为:

二、南京市新旧城区及其相互作用力的测算

(一)南京市新旧城区的界定

以往对南京内部区域空间的研究主要针对主城区范围，依据建设的时序可将主城区划分为：新旧两城区。旧城区，也就是老城即明城墙以内部分；新城区指明城墙以外的城市地区。为方便研究，突出主要问题，本节研究旧城区范围指玄武、白下、秦淮、下关、建邺、鼓楼等六城区，而新城区则包括浦口、六和、江宁、栖霞、雨花台等五郊区。

(二)南京市新旧城区空间相互作用力的测算

南京市旧城与新城空间相互作用力的计算，首先是对南京市新旧城区综合质量K的计算，即对分子的计算；其次是对南京市新旧城区区间距离内涵的深化，即对分母的计算。

第一步骤：选用主成分分析法，对南京市旧城与各新城区的综合质量指数K进行计算。

(1)指标遴选。在选取如何评定南京市旧城与新城区的综合质量指数的指标时，应遵循数据的完备性、精炼性、科学性和可行性原则[8]。依此原则，我们遴选出如表1所示的有效指标。

(2)由于各指标原始数据代表的物理含义不同，存在着量纲上的差异，会影响到整体评价。所以要对数据进行标准化处理，所用公式为:若，令，通过直线型无量纲化处理，其结果如表2所示。

(3)进行主成分分析。利用主成分分析法计算结果如表3所示。

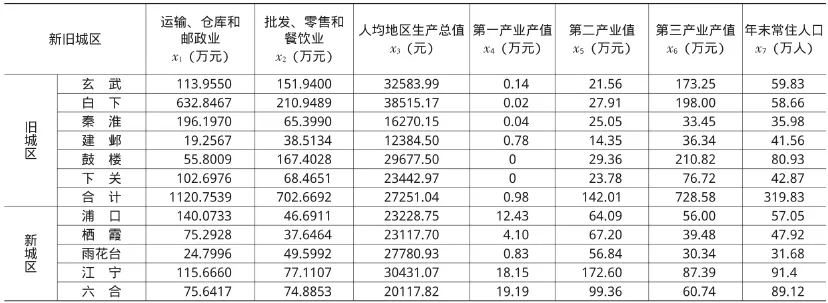
表1 2011年南京市新旧城区质量综合评定指标及原始数据

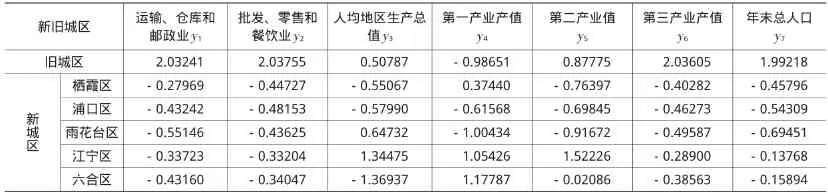
表2 南京市新旧城区质量综合评定标准化数据表

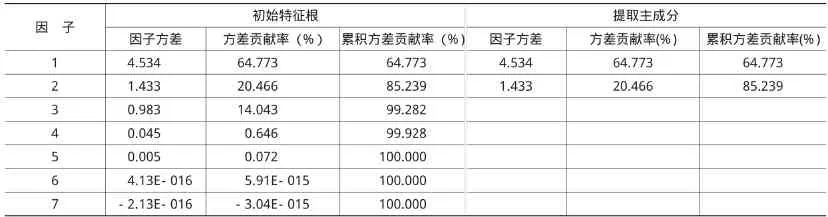
表3 全部解释方差表

从表3中可以看出，表中7个原始变量的数值变化，主要由前三项主成分的数值来表示。

(4)权重确定。μi为特征值。

(5)计算南京市旧城、各新城区的综合质量指数K。其中wi为权重，zi为主成分值。

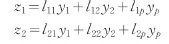
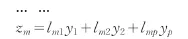
式中lij为主成分载荷，yi为标准化后的指标数据。结合表4数据，计算结果如表5所示。

表4 主成分载荷值矩阵

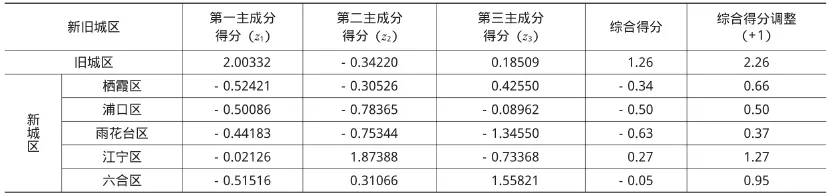
表5 南京市新旧城区综合质量评定结果

第二步骤：关于旧城与各新城区距离的计算。

针对不同运输方式的权重、时速以及货币成本，结合南京市旧城至新城区的交通运输方式，可以做如下假设(如表6、表7所示)。

(1)若旧城与新城区之间只有一种运输方式，即λ=1；若旧城与新城区之间有两种运输方式：一般公路与铁路组合时，λ1=0.9(一般公路)，λ2=0.1(铁路)；若旧城与新城区有三种运输方式：一般公路、高速公路、铁路同时拥有时，λ1=0.3(一般公路)，λ2=0.6(高速公路)，λ3=0.1(铁路)。

(2)设定旧城到新城区一般公路运输的平均时速为80km/h，高速公路运输的平均时速为100km/h，铁路运输的平均时速为60km/h。

(3)设定铁路的运输成本为0.5，一般公路的运输成本为1，高速公路的运输成本为1.5。

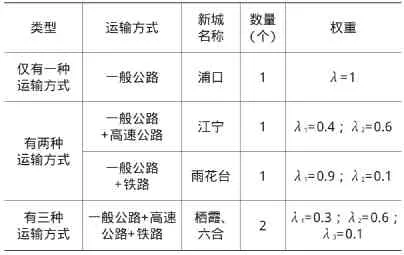
表6 南京市新旧城区不同运输方式

表7 南京旧城到新城区的运输方式权重与时速

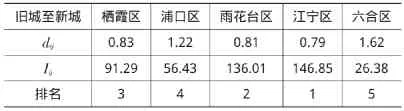
表8 南京市新旧城区空间相互作用力

三、结 论

综上所述，可以得出以下结论：

第一，南京新旧城区间距离的远近不再是新旧城区间空间相互作用的唯一决定性因素。在本文中，南京旧城到新城区雨花台区、栖霞区的空间距离相近，但旧城与两区的空间相互作用力相差较大。这说明两地的空间相互作用力并不是只受两地距离这一单一因素影响，还有影响地区间经济引力的“距离”，除此之外，还受多种因素的影响。因此，对于南京的扩容扩建来说，在制定城市发展规划及经济社会一体化政策时，一方面要充分考虑到有效促进新旧城区的良性互动，同时，还应把其他影响和制约城市空间相互作用的多层因素充分考虑在内。

第二，为增强对城市空间相互作用理论运用的科学性和说服力，本文在坚持引力模型基本原则和步骤的前提下，在实际研究时，对引力模型中分子和分母的内涵进行了深度拓展。本文选取能对区域间产生空间相互作用的人均地区生产总值、第一、第二和第三产业生产总值等多个有效指标，利用主成分分析法对区域间的综合质量K进行了综合评定，使分子的内涵得到进一步拓展。在某种程度上，多种指标来衡量两地质量可以更为精确地测算出南京市新旧城区空间相互作用力的大小，减少了不必要的误差。

随着各种新型运输工具的出现，21世纪交通的特点可以浓缩为“高速”两个字。从古代的“日中为市”，发展到现在的“三小时经济圈”，已在向传统的距离概念挑战，在交通便捷的地方，空间上的距离被大大缩短了，距离也可以用时间、运输成本等特殊距离单位来诠释。因而本文用各种运输方式的权重、时速、货币成本等指标代替了传统意义上的距离，进一步深化了分母的内涵。

第三，由于引力模型本身的局限性，通过其测算得到的结果是静态的，而事实上，把空间上彼此分离的南京新旧城区结合为具有一定结构和功能的有机整体的空间相互作用力，是在不断变化的。因此，在今后不断深化研究中，可以先用计算简便、易于掌握和理解的静态均衡分析法测算出每年南京市新旧城区间引力的变量，然后将以往测算的结果作为样本数据，利用实用和精确的神经网络方法进行数据拟合处理，从而科学地预测出南京市新旧城区之间的相互作用力，以便更精准地对其进行有效评价。

［1］国务院发展研究中心课题组.世界城市化和城市发展的若干新趋势和新理念［J］. 中国发展观察，2013(1)：35-38.

［2］龙青云.城市间相互作用的万有引力模型分析［J］.湖南经济管理干部学院学报，2005(5)：48-49.

［3］李江苏，骆华松，曹洪华.基于引力模型分析城区与郊区空间相互作用—以昆明市为例［J］.经济问题探索，2008(12)：53-58.

［4］孟德友，陆玉麒，史本林.基于路网的江苏城市空间相互作用测度［J］. 商丘师范学院学报，2009(9)：112-118.

［5］李小建.经济地理学［M］.北京:高等教育出版社，1999.

［6］吴殿廷.区域分析与规划高级教程［M］.北京：高等教育出版社，2004.

［7］魏后凯.现代区域经济学［M］.北京:经济管理出版社，2006.

［8］陶长琪，齐亚伟.我国区域经济差距的空间演变趋势及其成因［J］. 徐州工程学院学报，2011(5)：44-47.