双驱动六点支承平台设计及调平算法＊

王大志，谢占功，何 凯，杜如虚

（1.广州中国科学院先进技术研究所 精密工程研究中心，广东 广州 511458；2.中国科学院深圳先进技术研究院 精密工程研究中心，广东 深圳 518055）

引 言

调平是精密仪器及机械领域常见的一类问题。如经纬仪、陀螺罗盘以及雷达等仪器设备的工作都需要一个水平基准［1－3］。调平对充分发挥这些仪器设备的精度和工作能力，提高其机动性具有重要意义。因此，作为军事及民用等领域广泛应用的一项基础技术，平台调平受到国内外相关研究人员的普遍关注。

三点支承是精密机械设计中的一个重要概念，它是指不共线的三点可以确定一个平面。因此，具有三个可调支承点的调平机构是一种自然的设计方案，一个容易忽视的问题是：三点支承平台属于欠约束、欠驱动系统。在自然状态下仍具有某些自由度，平台的稳定性差，不利于设备的精度保持；在输入状态下，平台处于欠驱动状态，为实现平台调平，需要考虑平台运动的几何因素及平台支承与底面之间的摩擦力，在控制上比较复杂［4－5］。针对这一问题，提出了一种双驱动六点支承平台，并介绍了该平台的调平算法及实验结果。

1 双驱动六点支承平台

历史上有两种六点支承夹具，分别称为3V夹具和Kelvin夹具［6－7］，如图1和图2所示。

图1 3V夹具Fig.1 3Vclamp

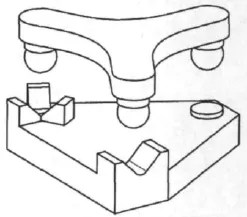
图2 Kelvin夹具Fig.2 Kelvin clamp

这两种夹具主要用于精密定位，已经存在100多年了。它们在自然状态下均具有确定位姿，不存在三点支承结构的欠约束问题。因此，考虑用它来做调平机构的支承。然而这两种夹具均是圆周对称结构，加入三个螺旋输入后，在调平时会出现运动干涉，而使用正交结构则有可能避免这一问题。鉴于这些原因，提出了双驱动六点支承平台结构，如图3所示。

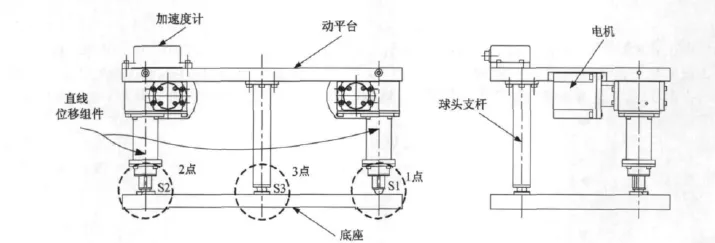
图3 双驱动六点支承平台Fig.3 Leveling stages with six－point supports and two inputs

该平台仅具有两个直线位移输入组件，减少了驱动元件的数目。所谓六点是指球头S1与平面形成一点接触，S2与V型槽形成两点接触，S3与锥孔形成3个非冗余约束点，由此形成六个非冗余接触点。这种约束模式保证了机构的确定位姿和确定运动，由此解决了三点支承平台的欠约束和欠驱动问题。需要说明的是这里的六点是指六个非冗余约束点。

在结构上，双驱动六点支承平台包括动平台、底座、加速度计、直线位移组件以及球头支杆。在电机的驱动下，直线位移组件的球头支承产生直线位移，用以驱动平台转动。球头支杆的球头与底座上的锥孔构成平台的运动支点。

2 调平算法

调平的目的是使仪器工作的基准面与水平面重合。所谓水平面是指与重力加速度方向垂直的平面。因此，调平本质上是使平台的法线与重力加速度方向重合。从这一角度出发，本文提出一种基于重力加速度方向矢量的调平算法。如图4所示平台处于水平状态，则平台法线矢量N与重力加速度方向矢量G重合。如图5所示平台处于非水平状态。此时平台的法线矢量N与重力加速度矢量G之间存在一个夹角。本质上，如果使平台的法线矢量与重力加速度矢量重合，那么就实现了调平。因此，无需直接关注平台的运动变化，而仅需关注平台的法线矢量与重力加速度矢量是否重合，由此将平台的调平问题转化为平台法线矢量的空间运动变换问题。

图4 平台水平状态Fig.4 Leveling conditions of stages

图5 平台倾斜状态Fig.5 Tilt conditions of stages

设平台的法线矢量N和重力加速度矢量G分别为：

设存在过渡矢量M，则平台法线矢量N绕x轴转动θ到过渡矢量M，然后过渡矢量M绕y轴转动φ到重力加速度矢量G。且设过渡矢量M＝（mxmymz）T，分别确定平台法线矢量N和过渡矢量M 在x轴的投影，过渡矢量M和重力加速度矢量G在y轴的投影。令X0和Y0分别表示x轴和y轴方向的单位矢量，则：

可得：

则：

由此可得过渡矢量：

设法线矢量N绕x轴转动θ到过渡矢量M，然后过度矢量M绕y轴转动φ到重力加速度矢量G，PX与QX分别是N和M 在垂直于x轴方向平面的投影，则：

可得转动角度θ：

同理，设PY和QY分别是M 和G在垂直y轴方向平面的投影，则

可得转动角度φ：

转角θ和φ的存在证明了仅通过两个输入可以实现平台的调平，同时给出了实现调平的转动角度。

在此基础上编写了调平软件，软件主要包括控制卡初始化，数据采集、平台转角等程序模块。通过调用初始化函数可对控制卡进行初始化；数据采集模块的功能是为了获取平台的重力加速度数据；平台转角模块可使系统根据转角并通过脉冲当量计算电机需要发送的脉冲数。调平程序流程如图6所示。

当平台倾角不大于0.002°时即认为平台达到水平，并以此作为程序的判断条件。

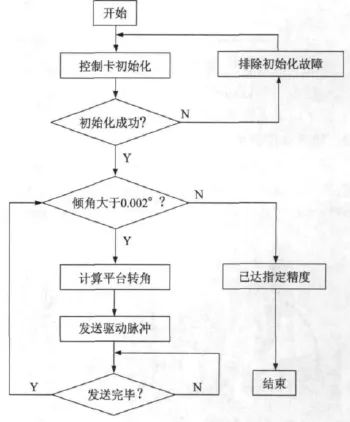
图6 调平程序流程图Fig.6 Flow chart of leveling program

3 调平实验

调平实验旨在验证两输入调平算法，并对平台重复精度进行测试。调平实验系统主要包括平台本体、加速度计、步进电机、驱动器、控制卡以及PC机。将加速度计量值通过三角关系转化可得角度值，倾角模型如图7所示。

3.1 两输入调平算法验证

首先通过传感器测量平台当前的倾角θx和θy，可以将加速度计量值转化为倾角；然后，根据双输入调平算法可计算两驱动器的直线位移Δlx和Δly。那么，当两直线驱动器相应的伸长或缩短Δlx和Δly时，理论上，平台应达到水平，即平台此时的倾角Δθx和Δθy应等于零。考虑到零件加工以及传动误差等因素，倾角Δθx和Δθy应接近于零。为此，对平台随机测量10次，实验数据如表1所示。

图7 倾角模型Fig.7 The tilt model

表1 两输入调平算法验证数据Tab.1 The validation data of leveling algorithm using two inputs

由表1可以看出，平台在一定的倾角θx和θy下，输入一次位移控制量移Δlx和Δly后，平台倾角Δθx和Δθy趋近于零，这表明算法具有较好的收敛性。如通过闭环控制，则可使平台达到指定的水平精度，由此验证了两输入调平算法的正确性。

3.2 重复精度测试

调平平台实验系统主要包括平台机械本体、加速度计、步进电机、驱动器、控制卡以及PC机。实验中分为两个测试状态。测试状态1是指将两直线位移组件的球头均调至最高点，如图8所示。测试状态2是指将一个直线位移组件的球头调至最高点，另一个直线位移组件的球头调至最低点，如图9所示。

图8 测试状态1Fig.8 Testing condition 1

图9 测试状态2Fig.9 Testing condition 2

在每组状态下，依次使球头变化3mm，连续测试6组数据，两个状态所测得数据如表2和表3所示。

表2 最高点状态Tab.2 Condition of highest points

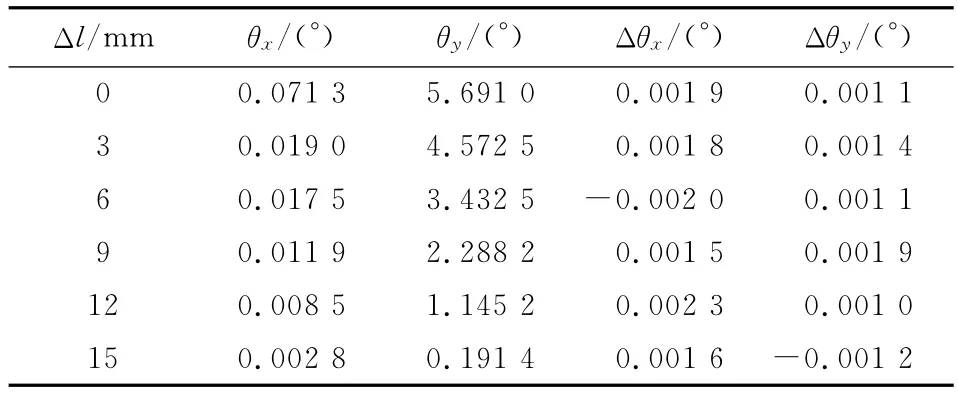
表3 最高点和最低点状态Tab.3 Condition of highest points and lowest points

平台在两个方向的重复精度分别为σx＝0.001 7°和σy＝0.001 1°，两个方向的水平重复精度优于0.001 7°。

4 结 论

双驱动六点支承平台采用机电式自动调平，水平重复精度优于0.001 7°，调平范围 ±5°。相比于三点支承平台，该平台具有如下几个特点：

（1）六点支承结构，即在自然状态下具有确定位姿，在输入状态下具有确定运动，由此解决了传统三点支承平台的欠约束和欠驱动问题；

（2）仅使用两个驱动，并可联动输入进行调平，减少了驱动元件的数目，简化了系统的结构；

（3）使用加速度计作为传感元件，相对于倾角传感器，该方法更加简单、响应速度快；

（4）重力加速度矢量调平算法具有物理概念清晰，数学方法严格的特点，可准确建立平台的运动模型。

此外，本文的工作深化了对调平问题的认识，分析了“三点确定一个平面”与“调平”的问题。三点可以确定一个平面，但这并不意味着调平需要使用三个脚螺旋。三点确定一个平面仅是一个几何概念，它与物体的调平是不同的两个问题。从运动学的角度，调平是对物体两个转动自由度的调整。

双驱动六点支承平台是一种新型二自由度球面并联机构，动平台的运动属于二自由度定点运动。由于光束在空间的指向仅需两个参数即可确定。因此，平台的这种二自由度定点运动对光束的指向控制具有潜在的应用价值。例如用作大口径反射镜架［8－10］或并联光电跟踪平台等，未来将就这方面的研究进行报道。

［1］姜伟伟，高云国，冯栋彦.大型光电设备基准平面自动调平系统［J］.光学 精密工程，2009，17（5）：1039－1045.

［2］高福晖.机械零件强度许用值新标准及大型经纬仪机械设计［M］.成都：成都科技大学出版社，1998：202－210.

［3］李勇建，魏贵玲，邓劲松，等.自动调平技术研究［J］.压电与声光，2010，32（6）：949－952.

［4］王大志.应用运动学原理的双驱动六点支承平台设计与调平方法研究［D］.北京：中国科学院研究生院，2012.

［5］王大志，何 凯，杜如虚.精确约束二自由度微动角位移机构设计［J］.光学 精密工程，2011，19（8）：1874－1882.

［6］HALE L C，SLOCUM A H.Optimal design techniques for kinematic couplings［J］.Precision Engineering，2001，25（2）：114－127.

［7］SLOCUM A H.Precision machine design［M］.Michigan：Prentice－Hall Inc.，1992.

［8］朱耆祥.ICF用阵列镜腔及阵列伺服反射镜的新型反射镜结构［J］.光电工程，2001，28（5）：24－27

［9］章亚男，沈丽丽，沈卫星，等.大口径透镜姿态调整机构的支承分布［J］.光学 精密工程，2010，18（12）：2624－2632.

［10］沈丽丽，章亚男.大口径非圆透镜的夹持设计［J］.光学仪器，2011，32（5）：49－53.