一种光学元件面形三维重建的算法研究＊

穆 绵，刘缠牢

（西安工业大学 光电工程学院，陕西 西安 710021）

引 言

随着光学技术的发展，光学元件的应用日益广泛，因此对光学元件的质量检测提出了更严格的要求。针对市场需要实现非接触在线检测的要求，提出一种基于结构光的三维检测方法，目前这种方法多用于检测高反射率的物体，因此将此方法运用于检测光学元件面形是一种新的尝试。基于结构光的三维检测方法对于周围的检测环境要求较低，可用于工厂实现光学元件面形的在线检测。

1 测量原理

本文探究的是基于线结构光扫描测量（光切法）［1－2］和立体视觉测量（双目立体视觉法）［3－4］相结合的一种检测光学元件面形的测量方法，测量原理如图1所示。一定模式的结构光投射到被测物表面，相机采集受被测面形调制的光条图像。

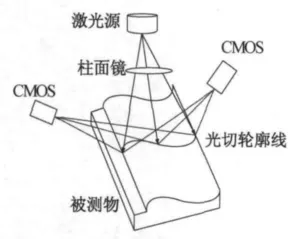
图1 线结构光视觉法测量原理图Fig.1 Schematics of line structure light vision measurement

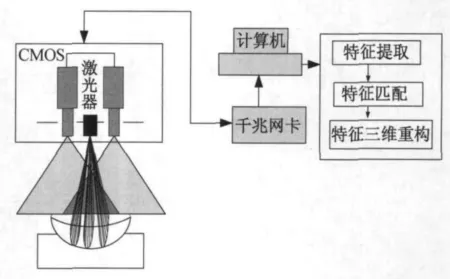
图2 投影法检测光学面形的设计方案Fig.2 Design scheme of optical surface characterization inspection by projection method

2 实验方案设计及图像采集

根据测量原理，设计投影法检测光学面形方案如图2所示。将两个CMOS相机平行放置，再将线激光器放置在两个摄像机中间并垂直平分两相机连线。线结构光垂直水平面投射被测物体表面产生三条亮度很高的细线，左右相机采集到线结构光条的图像，利用结构光平面标定技术，可以得到光条图像坐标和世界坐标之间的转换关系，实现三维坐标测量。

在实验中，由于客观条件的限制，采用单线激光器对光学元件表面扫描，电控平移台每移动0.5mm，相机采集得到一组左右视图，故实验过程共采集得到了12组图片（任选一组左右视图如图3所示）。图4给出了对采集得到的图片进行软件编程算法的流程图。

图3 原始图像对Fig.3 Untreated images

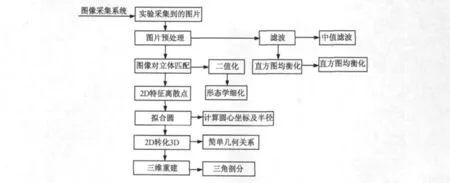
图4 软件算法流程图Fig.4 The flow chart of software algorithms

3 数学模型

3.1 摄像机的成像模型

定义图像坐标系（u，v）、摄像机坐标系（Xc，Yc，Zc）和世界坐标系（XW，YW，ZW）来描述摄像机成像过程。设原点位于（u0，v0）像素点上，这三个坐标系之间的关系见下式：

式（1）中，dx×dy是像素点的大小，以mm为单位；0T是零矩阵的转置矩阵。A只与摄像机内部结构有关，称其为摄像机内部参数；R，T完全由摄像机相对世界坐标系的方位决定，称为摄像机的外部参数［5］。

由此可知，若已知摄像机的内外参数A，R，T以及图像上坐标点的位置（u，v），就可以得到空间坐标点。摄像机标定的过程，就是求解摄像机内外参数的过程。

3.2 参数标定

采用文献［6］中二维平板的标定法，标定程序的流程图如图5所示。

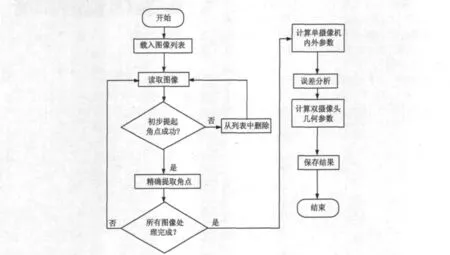
图5 标定的流程图Fig.5 The flow chart of calibration

根据平面棋盘格及公式，得出的标定结果如表1所示。

4 图像处理

将采集得到的原始图像对进行中值滤波去除孤立图像噪声，得到的其中一组图像对如图6所示。

滤波后的图像对在视觉上与原图像并无差别，所以在对滤波后的图像进行直方图均衡化来平衡图像对之间的亮度差异，可以更清楚直观地观察到透镜与光线的轮廓，直方图均衡化的图像对如图7所示。经过直方图均衡化后，立体图像对的亮度差异降低，且亮度明显提高，较原图来说可以直观地看到透镜与光线的轮廓。

至此，经过图像预处理的立体图像对，亮度差异得到改善，灰度均匀地分布在0～255之间，能够较好地满足后面立体匹配的要求。

表1 标定结果Tab.1 Result of calibration

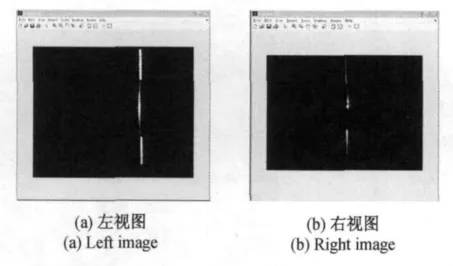
图6 滤波后的立体图像对Fig.6 Images from median filter

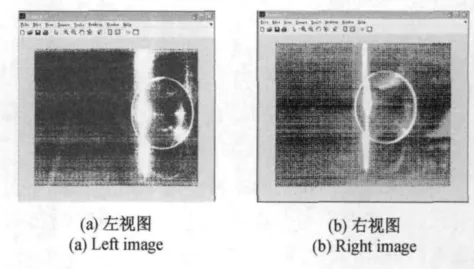
图7 直方图均衡后的立体图像对Fig.7 Images after histogram equalization

4.1 基于区域的立体匹配

基于区域的立体匹配［7－8］就是要衡量像素邻域（窗口）之间灰度或纹理的相似性。匹配实验选用像素数为9×9的匹配窗口，以及式（2）所示的最小绝对差算法SAD算子来进行描述，在匹配完成之后需要利用式（3）进行视差图的校正。

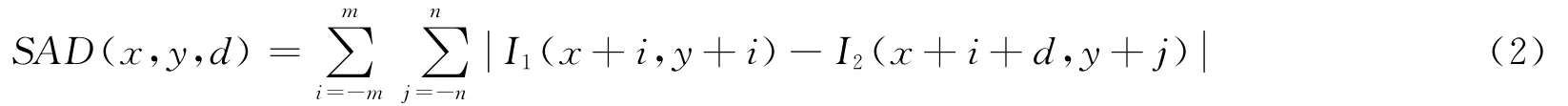
式（2）中，I1为左图像上任意一点，I2是右图像上I1的匹配点，d为搜索范围。

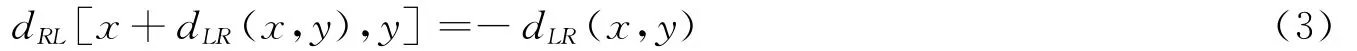
式（3）中，dRL是以左图为基准，右图相对于左图的视差；dLR是以右图为基准，左图相对于右图的视差。

从实验得到的12组图片中选择效果较好的3组图片进行立体匹配，并采用左右一致性检验、中值滤波，二值化等处理，最终输出视差二值化图像如图8所示。

4.2 曲线拟合

立体匹配后的视差二值化图需要确定其圆环中心点的位置，从3组立体匹配的视差图中提取多个点，采用最小二乘法来拟合圆与曲线得到圆心坐标及半径，拟合结果如图9所示。

图8 透镜面形视差图Fig.8 Parallax image of lens surface characterization

图9 视差图拟合Fig.9 Parallax image fitting

现以图9（c）组拟合圆的圆心和半径为基准，将图9（a），图9（b）拟合圆叠加在图9（c）拟合圆上，从而构建成设计方案所述的三线激光投影的模型，拟合结果如图10所示。

4.3 三维重建

在完成的拟合图中选取多个二维平面坐标点，利用3节介绍的空间点坐标计算方法可得出透镜表面的空间离散点集。三角剖分采用 Delaunay 标准的 Bowyer－Watson算法来实现［9－10］，剖分图如图11所示，并最终在OpenGL中得到透镜模型的三维立体图像，如图12所示。

图10 三线激光投影拟合图Fig.10 Fitting image of 3－ray laser projection

图11 透镜三角剖分过程图Fig.11 Lens triangulation process

图12 透镜三维重建Fig.12 Lens model 3Dreconstruction

4.4 实验结果

具体计算重构三维面形的2点PV值，20点PV值和均方根误差（RMS值），并与单线扫描法检测的相应结果比较（见表2）。由于单线扫描法检测光学元件面形的技术目前已经较为成熟，故将三线投影法的检测结果与之比较即可验证可行性。

从测量结果比较可以看出，三线投影法与单线扫描法的PV值的差异约为0.02μm，对于RMS值，两者的差异约为0.03μm，这个结果是较为理想的，与干涉检测法和数字刀口检测法的精度是较为接近的，从而验证了结构光投影法检测光学元件是可以满足通常的测量要求，具有一定的可行性。

表2 测量结果比较Tab.2 Comparison of the measurement results

5 结 论

本文采用投影法检测光学元件面形，即线结构光扫描测量和立体视觉测量相结合的检测方法，这种方法最终剖分得到的透镜模型图像初步具有真实透镜模型的三维外貌形状。但由于计算误差、匹配精度、图像采集环境等因素的影响，造成最后得到的三维图像有明显的变形。为了得到更完善更精细的重建图像，还需要进一步的研究和改进。

［1］孙国强，许增朴.用于产品造型设计的三维反求测量系统的研究［D］.天津：天津科技大学，2007.

［2］王晓林，陈伟民，黄尚廉.光切法三维轮廓测量的原理及其应用［J］.光学技术，1997，3（2）：39－43.

［3］陈 江.二目立体视觉测量系统关键技术研究［D］.南京：南京航空航天大学，2006.

［4］高 文，陈熙霖.计算机视觉—算法与系统原理［M］.北京：清华大学出版社，1999.

［5］宋 龙.线结构光实物反求测量仪的研究与开发［D］.哈尔滨：哈尔滨理工大学，2008.

［6］李洪海，王敬东.摄像机标定技术研究［J］.光学仪器，2007，29（4）：7－11.

［7］达飞鹏，盖绍彦.光栅投影三维精密测量［M］.北京：科学出版社，2011.

［8］HIRSCHMULLER H.Improvements in real－time correlation－based stereo vision［J］.IEEE Workshop on Stereo and Multi－Baseline Vision，2001，22（11）：141－148.

［9］程晓亮.基于双目立体视觉的三维重构研究［D］.哈尔滨：哈尔滨工业大学，2006.

［10］WATSON D F.Computing then－dimensional Delaunay tessellation with applications to Voronoi polytopes［J］.The Computer Journal，1981，24（2）：167－172.