一种新型阈值函数在图像去噪中的应用

岳 洋

(吉林化工学院理学院，吉林吉林132022)

一幅图像从摄取到编码传输都不可避免地会混入噪声信号，而这又使得对图像边缘的精准检测［1］、特征的准确提取［2］以及压缩等一系列的后期操作都会受到很大的影响，这就意味着去噪是图像处理中十分重要的一个环节.近年来由纯粹数学里发展而来的小波变换，因为具有多分辨率以及自由选择基函数等特点，使得它在图像去噪领域发挥了前所未有的重要作用.

Donoho等人于1995年提出了基于小波变换的软、硬阈值函数去噪方法［3］.效果显著应用广泛.但此方法存在一个明显的不足:在存在间断点的范围内出现了Gibbs现象.后来，Coifman与Donoho联合提出了平移不变法［4］，即对信号的循环位移用以消除人造伪影.平移不变法又被Bui和Chen应用到多小波［5］，仿真效果表明多小波平移不变法比单小波平移不变法能有更好的去噪效果.之后，基于邻域系数的阈值方案被Cai和Silverman［6］提出，比起传统的逐个小波去噪方法，实验结果表明此种方法具有一定优势.小波邻域阈值法后来被Chen和Bui［7］推广到了多小波，把其应用到标准测试图像中发现，邻域多小波法的去噪效果优于邻域单小波去噪法.基于小波系数在同一子带的相关性这一事实基础上，Sendui和 Selesnick［8-9］又提出了双元阈值去噪法.

1 小波阈值去噪的原理

Donoho于1995年所提出的软、硬阈值函数法，其算法简单，去噪效果较好，在实际中得到了广泛的应用.正交小波变换能使信号中的能量主要集中在一些大的小波系数中;但是，噪声的能量却在整个小波域内分布，所以，信号经小波分解后，它的小波系数值要大于噪声的小波系数值.那么就可以理解为，信号的主要信息包含在幅值比较大的小波系数中，而噪声的信息则包含在幅值比较小的系数中.那么，可以通过设定阈值就可以把包含信号信息的系数保留，而把大部分的噪声的小波系数变为零.也就是说，对于那些大于阈值的小波系数，可以被认为是包含有用信息的信号的分量，这是就要把这种小波系数维持原有的值不变，反之，对于那些小于阈值的小波系数，则可以被认为是由含有噪声的信号分量变换得到，此时把此种信号去除.此法存在着缺点，软、硬阈值函数的光滑性很差，这会使得经小波系数重构后的图像信号产生Gibbs现象［9］，软阈值函数中总是有固定的偏差存在于原始信号的小波系数和经阈值函数作用后的小波系数，这就使得原始图像的特征不能很好的得到保留.

在做具体的小波变换之前，要先选择合适的小波基函数对图像进行小波分解，获得其小波系数.设:φ(t)∈L2(R)其傅立叶变换为Ψ(w).当满足条件时，则称φ(t)为一个基

本小波，将此基本函数φ(t)做伸缩和平移变换后，就可以得到一个函数序列:

a，b∈R，a∉0，且a为伸缩系数，b为平移系数.一幅图像可以看成是一个二维函数，则它的小波变换为:

和式(2)对应的f(x，y)重构公式是:

二维离散小波变换的分解与重建都采用Mallat快速算法［10］.

2 阈值函数的选取

阈值函数的构造是去噪问题的关键所在，还有如何选择小波基函数用以分解图像也十分重要.只有综合考量这两方面因素，理想的去噪效果才能实现.

2.1 Donoho的阈值函数

硬阈值函数:

2.2 构造新的阈值函数

只是被软阈值函数处理过的小波系数，它与原始信号的小波系数总存在一个恒定的差值，为了最大限度的保存图像的原有信息，必须把这个差值变小，但却不能把其变为零，否则便是硬阈值函数了，所以，本文构造新阈值函数的出发点就是让处理后的小波系数介于(|wj，k|-λ)与|wj，k|之间.基于上面的分析，用加权方法来构造阈值函数，其表达式如下:

其中，wj，k为小波系数，λ 为阈值

其中，t为任意大于零的常数.

2.3 新阈值函数与软、硬阈值函数的关系

从图1可以看出，新的阈值函数继承了软阈值函数的连续性，同时光滑性得以改善.考察新阈值函数的原型:

显然，

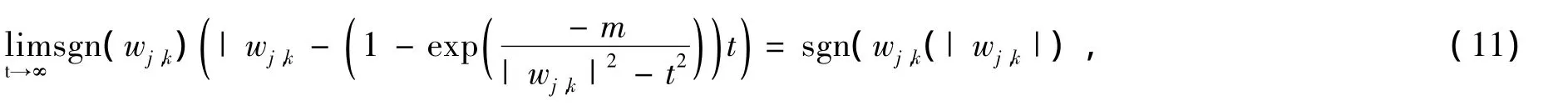
式(10)和(11)说明随着t→∞，式(6)为软阈值函数;而随着t→0，式(6)为硬阈值函数.可见，新阈值函数是在软硬阈值函数之间的一个折中，可以通过t的取值的变化，找到去噪效果好的阈值函数.

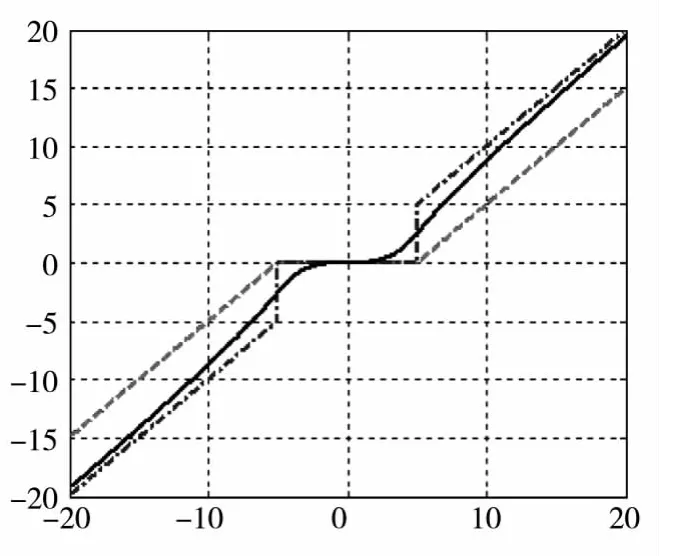
图1 三种阀值函数的示意图

3 实验结果与讨论

为了说明新构造的阈值函数比原来的软、硬阈值函数在去噪过程中表现优越，本文在MATLAB R2009a中，对一幅通用的图像分别用新构造的阈值函数与软、硬阈值函数进行了测试，图像的原始尺寸为，位灰度图像，对其加入均值为零，方差为0.02的高斯白噪声.设原始图像为

重构图像为:

通过峰值信噪比(PSNR)、均方误差(MSE)这两个指标来比较，其表达式［11，12］为

三种阈值函数的测试结果见表1，仿真结果见图2.

图2 仿真实验结果比较

表1 三种去噪方法的比较

4 结 论

可以看到，相对于软、硬阈值函数法，本文构造的新型阈值函数不仅有效地去除了高斯噪声，而且比较好地保留了图像的细节信息，改善了图像的峰值信噪比.

［1］张秀兰.基于MATLAB的数字图像的边缘检测［J］.吉林化工学院学报，2010，27(2):59-61.

［2］甘树坤，吕颖，吕雪飞，等.人脸检测中的图像光照处理研究［J］.吉林化工学院学报，2011，28(9):52-55.

［3］D.L.Donoho De-noising by Soft thresholding［J］.IEEE.Trans Inform Theory，1995，41(3):613-627.

［4］R.R.Coifman，D.L.Donoho，Translation invariant denoising，in:Wavelets and Statistics，SpringerLectureNotesinStatistics，vol.103，Springer，New York，1995，pp.125-150.

［5］T.D.Bui，G.Y.Chen，Translation invariant denoising using multiwavelets，IEEE Trans.Signal Process.1998，46(12):3414-3420.

［6］T.T.Cai，B.W.Silverman，Incorporating information on neighbouring coefficients intowavelet estimation，Sankhya:Indian J.Stat.Ser.2001，63(2):127-148.

［7］G.Y.Chen，T.D.Bui，Multiwavelet denoising using neighbouring coefficients，IEEE Signal Process.Lett.2003，10(7):211-214.

［8］L.Sendur，I.W.Selesnick，Bivariate shrinkage functions for wavelet based denoising exploiting interscale dependency，IEEE Trans.Signal Process.2002，50(11):2744-2756.

［9］L.Sendur，I.W.Selesnick，Bivariate shrinkage with local varianceestimation，IEEE Signal Process.Lett.2002，9(12):438-441.

［10］St＇ephane Mallat a wavelet tour of signal processing［M］.USA:Elsevier，2009.

［11］关履泰.小波方法与应用［M］.北京:高等教育出版社，2007.

［12］潘泉，张磊.小波滤波方法及应用［M］.北京:清华大学出版社，2005.