基于贝叶斯决策的网格计算资源分配算法

李 昊，谢中江，侯哲生

(1.吉林师范大学计算机学院，吉林四平136000;2.吉林凯赛生物技术有限公司，吉林吉林132021;3.吉林化工学院机电工程学院，吉林吉林132022)

网格计算不同于常规分布式计算，网格环境的异构性和复杂性使得资源分配面临很多不确定因素的影响，为了进行最优的资源分配，Martino等人提出了一些基于最优化理论的任务调度算法，比如依据遗传算法［1-3］、蚁群算法［4-6］、函数构造法［7-9］等，这些算法从不同角度对任务调度最优解进行求解，均取得较好效果.在对任务进行资源分配的过程中，资源的状态并非一成不变的，一个有效的任务调度算法，应该有效利用资源预报系统，对分配决策进行及时调整.网格计算中可以应用 NWS［10］、RPS［11］等基于时间序列的资源预报系统进行资源状态的实时预报及分析.基于贝叶斯决策的网格计算资源分配算法正是应用了资源的预报和分析，将完全不确定型决策引入到任务调度算法中，更好的实现负载平衡和用户QoS要求.

1 基于贝叶斯决策的决策模型

对用户任务分配网格资源，可以看成是完全不确定型决策问题，网格计算的主要特点是网格结构的异构性、网格服务质量的不确定性，当用户提交任务，任务运行情况取决于资源分配算法的优劣，当用户任务有明确的完成时间要求时，资源分配不当会带来一定的风险.在分配决策过程中可能会出现多种无法预料的状态，这些事件出现的概率估计的正确程度直接影响到决策中收益期望值.为了更好的进行决策，在条件许可的情况下，可以进一步补充一些新的信息.补充信息可以通过计算机网络以及网格应用程序执行性能监控和预报系统获得.获得新信息后，可以根据这些补充信息修正原来状态时间出现的概率，并利用修正的概率分布重新进行决策.由于这种概率修正主要根据贝叶斯(Bayes)定理进行，故称这种决策为贝叶斯决策.

1.1 分配算法的步骤

基于贝叶斯决策的网格计算资源分配算法通常分为3步进行.

1.1.1 根据先验概率进行决策

网格资源分配算法首先根据以往情况及经验对这些事件出现的概率进行估计，即得出先验概率，然后依据先验概率分布及期望值准则做出决策，选择出最优方案，并得出相应最优期望值，记为EMV*(先).这也是多种任务调度优化算法的调度依据部分，由此得到的调度决策是本次用户任务调度的基础.

1.1.2 预验分析

用户任务开始调度，分配资源进行计算，资源的性能状态和负载开始变化，依据之前信息的调度算法将无法适应新的变化，此时需要及时补充新的信息，在NWS等系统中，分布在资源上的sensor将周期返回状态信息，并进行资源预报.在补充新信息之前，对补充新信息是否合算做出分析，从而决定是否补充新信息.

1.1.3 后验分析

根据获得的新信息，对先验概率分布进行修正，得到后验概率分布，在此基础上做出决策，并计算出补充信息的价值.

1.2 分配算法的收益分析

因为性能监控和预报系统的预报准确程度以及本身就消耗掉的资源都是我们要考虑的因素.在Nimord/G［12］等基于经济学资源分配和任务调度系统中，补充新信息意味着额外的费用开销，采用了新信息则要求有明显的收益.下面给出收益分析的具体方法.

1.2.1 确定已有的资源状态θi，给出资源系统对应状态出现的概率值.根据当前状态进行最优调度算法的计算，确定调度方案dj在每种资源状态θi的效益值uij，根据期望值准则，计算各方案效益期望值:

相应最优方案及期望值

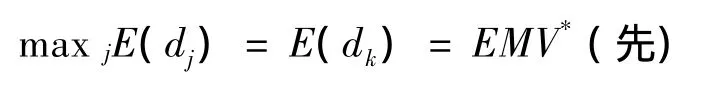
1.2.2 接下来的预验分析中，要估算出完全信息的价值(任何信息的价值均不会超过完全信息的价值)，并以它作为标准.当完全信息预报出现θk状态时，问题变成确定性决策问题.最优方案显然应由下式确定:

在完全信息下，决策所能获得的最大收益期望值:

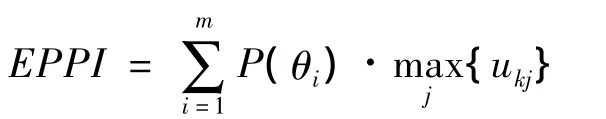
EPPI和EMV*(先)的差额即由于理想化的预报资源状态，而即使调整调度策略而带来的收益值，定义为完全信息的价值，记为EVPI:

1.2.3 很显然，准确的预知资源接下来的状态是不可能的，调度算法只能根据预报系统返回的状态信息或者预报信息对之前的信息进行修正.通常，补充的新信息是通过对x1、x2、……、xs共s个状态进行调查、实验，预报其中哪种情况将出现，同时通过资料获取条件概率P(xi|θj)，即实际出现状态θj而预报xj的概率.

在已知先验概率 p(θi)(i=1，2，…，m)及条件概率 P(xi| θj)(i=1，2，…，s;j=1，2，…，m)的基础上，利用贝叶斯公式可计算出修正概率，即后验概率:

根据计算的后验概率，可预先做出决策的框架.假设补充信息预报将出现xk状态，则用后验修正概率分布 P(θi|xk)(j=1，2，…，m)，计算各方案的期望收益值，并依据期望值准则进行决策，得

一旦得到补充信息预报，即可按上述方式进行决策.需要注意的是，补充信息通常具有不确定性，因而，这样的信息是不完全的，或说不是绝对准确的，因此，与完全信息相比，补充信息的价值不会大于完全信息的价值.

2 算法实现与分析

在文献［13］中，已经实现了结合网络资源预报的网络资源分配算法，采用NWS进行网络资源预报.在仿真试验中，假设用户任务deadline为3个时间单位，网格计算资源的可用性将决定用户任务的完成情况，如果任务顺利完成，产生效益5万元，不能完成将损失1万元，延迟运行，每时间单位损失0.2万元.根据以往经验，资源可用概率为30%.在该算法中，采用资源可用性预报，对资源可用的预报准确率为80%，对资源不可用的预报准确率为90%，预报需要支出0.08万元.

这里对100个用户任务进行随机模拟，得出未采用贝叶斯决策和采用贝叶斯决策平均效益值，算法运行结果如图1所示.

可以看出，采用基于经验期望值的网格任务调度算法，平均效益值(F1)要低于采用了贝叶斯决策的平均效益值(F2).而两者的差值大于预报支出费用，表明可以采用资源预报系统，提高决策的准确性.

图1 平均效益值计算结果

3 结 论

网格计算中任务分配，根据贝叶斯决策可以提高调度算法的平均效益值.在资源调度的过程中，如何增强资源状态预报的准确性，降低资源预报的费用，是提高该算法优越性需要下一步进行的工作.

［1］MARTINO D V.Sub optimal scheduling in a GRID using genetic algorithms［A］.Parallel and Distributed Processing Symposium［C］.2003，22-26.

［2］SONG S，HWANG K，KWOK Y K.Risk-resilient heuristics and genetic algorithms for security-assured grid job scheduling［A］.Com-puters，IEEE Trcmsactions［C］.2006，703-719.

［3］林剑柠，吴慧中.基于遗传算法的网格资源调度算法［J］.计算机研究与发展，2004，14(12):2195-2199.

［4］XU Z H，HOU X D，SUN J Z.Ant algorithm-based task scheduling in grid computing［A］.Electrical and Computer Engineering，2003.IEEE CCECE 2003［C］.2003，1107-1110.

［5］YAN H，SHEN X Q，LI X，et al.An improved ant algorithm for job scheduling in grid computing［A］.Machine Learning and Cybernet-ics［C］.2005，2957-2961.

［6］许智宏，孙济洲.用蚂蚁算法进行网格任务调度的研究［J］.计算机应用，2005，25(10):2236-2237.

［7］WANG T，ZHOU X S，LIU Q R，et al.OD:a general resource sched-uling algorithm for computational grid ［A］.Computer and Computa-tional Sciences，IMSCCS ＇06［C］.2006，644-647.

［8］王树鹏，云晓春，余翔湛.基于生存性和 Makespan的多目标任务调度算法研究［J］.通信学报，2006，27(2):42-49.

［9］季一木，王汝传.基于粒子群的网格任务调度算法研究［J］.通信学报，2007，28(10):60-66.

［10］Wolski R，Spring N，Hayes J.The Network Weather Service:A Distributed Resource Performance Forecasting Service for Metacom-puting［J］.Journal of Future Generation Computing Systems，1999，15(5/6):757-768.

［11］Peter A.Dinda Hallaron D R O.Host Load Prediction Using Linear Models［J］.Cluster Computing，2000，3(4):265-280.

［12］Buyya R.Nimrod/G Problem Solving Environment and Computational Economics.Grid Computing Environments Community Practice(CP)Document［M］.Global Grid Forum(GGF)/First GGF Workshop，Amsterdam，the Netherlands，2001.

［13］武秀川，李昊，鞠九滨.基于计算经济模型改善网格资源分发和发现的性能［J］.计算机工程与应用，2005，41(10):64-66.