截断参数对高斯光束俘获力的影响

李世磊，张耀举，赵 艳

(温州大学物理与电子信息工程学院，浙江温州325035)

作为一种微操控技术，光学俘获技术具有非接触、无损伤、高精度的特点.这项技术诞生［1-4］以来，在生物医药、物理等多个科研领域都得到了广泛的应用，相关的理论和实验研究层出不穷.研究光学俘获的射线光学模型(Ray Optics Model)由Ashkin建立［5］，之后，有很多科研工作者都应用该模型对光学俘获进行了研究.Leonardo André Ambrosio等人应用射线光学模型计算了双阴性微粒的俘获力［6］，另外还讨论了小折射率微粒的俘获力［7］和克服梯度力翻转的方法［8］;Richard Bowman等人基于射线光学理论讨论了利用空间光调制器在三维空间产生的不同形状的光阱的俘获能力［9］;Yanhua Wu等人考虑到微粒内部的复杂结构和表面性质，通过操控与细胞黏合的聚苯乙烯小球实现对细胞的操控［10］;Yanfeng Zhang等人应用射线光学模型研究了微粒的吸收系数和轴向位移对俘获力的影响［11］;Sung Hyun Kim等人研究了被俘微粒的大小对俘获力的影响［12］.

计算均匀分布的光束的俘获力对研究光学俘获的理论研究具有指导意义，但是现实中的光束一般都满足高斯分布，另外，偏振态的不同会产生不同的俘获力，径向偏振态的激光光束能产生较大的俘获力［13-15］.本文应用射线光学模型，研究利用功率恒定的高斯分布的径向偏振光俘获大折射率微粒时，截断参数对俘获力的影响.

1 俘获力的计算

对于单条光线，梯度力为入射光s波和p波的梯度力之和

其中:

散射力为为入射光s波和p波的散射力之和:

其中:

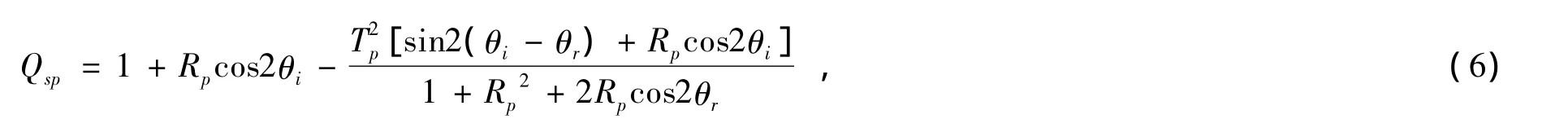
其中，θi和θr为光线的入射角和折射角，Rs和Rp为s波p波的反射率，Ts和Tp为s波和p波的透射率，fp和fsd分别为入射光中p波和s波占总功率的比例:

对于不同的偏振光，a和b取不同的数值，对于本文计算的径向偏振光，

其中，φ为入射光线与光轴的夹角，μ是入射平面与入射光和光轴Z轴所在平面的夹角，β0为入射光线的方位角.

对于整个高斯光束的俘获力，利用上述公式对能够经过透镜照射到微粒的光线进行积分后可以算出.

其中，r为光线的入射半径.

2 截断参数对俘获力的影响

截断参数的定义式为

其中RL为透镜的半径，ω0为光束的束腰半径.

在入射光功率恒定的情况下改变截断参数，能够通过透镜照射到微粒上的光线数量会随之改变，因而微粒所受到的俘获力也会发生相应的变化.

图1 截断参数β不同时高斯光束的轴向俘获力

图1依次给出了入射光功率相同的条件下，截断参数β为0.5、0.8、1.0、1.2时，高斯光束的散射力、梯度力以及合力的大小.纵坐标为无量纲数值Q的大小，横坐标为微粒的位置坐标，坐标原点选为粒子球心O，S表示球心O与焦点f之间的距离，R表示微粒半径，S/R大于零时表示微粒球心O位于焦点f上方，反之则为下方，而Z轴竖直向下.其中，红色、绿色、蓝色曲线分别代表了合力、梯度力、散射力的大小.被俘微粒折射率为1.6，所在介质为水，折射率为1.33.

很容易看出，梯度Qg力成反对称情况，说明微粒位置的改变会导致梯度力方向改变，但是方向总是将微粒拉向焦点f;而散射力Qs则为对称情况，证明散射力总是沿光线传播方向推动微粒.显而易见，最大值都出现在距离S/R的绝对值约等于1的位置，S/R的绝对值一旦大于1，则三个力的数值均急剧减小.这是因为当距离S等于微粒半径R的位置附近，光线的入射角θi和汇聚角φ都比较大，这样一来，梯度力在Z轴方向的分量Qgsinφ较大，而散射力在Z轴方向的分量Qscosφ较小，所以合力的效果总是将微粒拉到焦点附近.

图2 截断参数对轴向俘获力的影响

图2给出入射光功率一定时，截断参数对轴向俘获力的影响.五种颜色的曲线代表截断参数β取五个不同数值的情况下Q的取值.从图中可以看出，随着截断参数β的增大，表征合力大小的Q的最大值先增大，然后逐渐减小，图中所示情况中，截断参数β取值为0.8时Q最大.

图3给出了被俘微粒位于焦点上方且距离S与微粒半径R相等时，所受最大俘获力与截断参数的关系.可以很直观的看出，当入射光功率一定时，随着截断参数β越大，Q的值先增大，然后逐渐减小，这是因为:β很小的时候，光束束腰相对于透镜半径RL很大，因此光束中大部分光线都未能经过透镜照射到微粒上，所以微粒受到的俘获力很小;随着β的增大，进入透镜的光线越来越多，俘获力也随之增大.但是当β大到一定程度之后，Q的值随β的增大而减小，这是因为:所有的光线都更加靠近光轴，大角度的入射光线减少，光束的聚焦性减弱，导致光斑强度减小，从而导致俘获力减小，但是β的值不能太小，否则会造成很大的光能损失，入射光束的能量的利用率将大大降低.

图3 俘获力最大值随β的变化情况

3 结 论

在入射光功率恒定的情况下，利用径向偏振态的高斯光束俘获大折射率球形微粒时，选取适当的截断参数，能在保证激光光束能量的利用效率较高的情况下使尽可能多的大角度入射光经过透镜照射到被俘微粒上，进而获得较大的光场梯度，实现俘获力的最大化.

［1］A.Ashkin，Acceleration and trapping of particles by radiation pressure［J］.Physical Review Letters，1970，24:156-159.

［2］A.Ashkin，Atomic-Beam DeflectionbyResonance-Radiation Pressure［J］.Physical Review Letters，1970，25:1321-1324.

［3］A.Ashkin，Applications of Laser Radiation Pressure［J］.Science，1980，210:1081-1087.

［4］A.Ashkin，J.M.Dziedzic，and J.E.W.Bjorkholm，Steven Chu，Observation of a single-beam gradient force optical trap for dielectric particles［J］.Optics Letters，1986，11:288-290.

［5］A.Ashkin，Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime［J］.Biophysical Society，1992，61:569-582.

［6］Leonardo André Ambrosio，H.E.Hernández-Figueroa，Trapping double negative particles in the ray optics regime using optical tweezers with focused beams［J］.Optics Express，2009，17(24):21918-21924.

［7］Leonardo André Ambrosio，H.E.Hernández-Figueroa，Gradient forces on double-negative particles in optical tweezers using Bessel beams in the ray optics regime［J］.Optics Express，2010，18(23):24287-24292.

［8］Leonardo André Ambrosio，H.E.Hernández-Figueroa，Inversion of gradient forces for high refractive index particles in optical trapping［J］.Optics Express，2010，18(6):5802-5808.

［9］Richard Bowman，Graham Gibson，Miles Padgett，Particle tracking stereomicroscopy in optical tweezers:control of trap shape［J］.Optics Express，2010，18(11):11785-11790.

［10］Yanhua Wu，Dong Sun，Wenhao Huang，Mechanical force characterization in manipulating live cells with optical tweezers［J］.Journal of Biomechanics，2011，44:741-746.

［11］Yanfeng Zhang，Yudong Li，Jiwei Qi，et al，Influence of absorption on opticaltrapping force ofspherical particles in a focused Gaussian beam［J］.Journal of Optics A:Pure and Applied Optics，2008，8(5):11-13.

［12］Sung Hyun Kim，Hyun Ik Kim，Hyeong Joon Jun，et al，Beam Optics Approach to the Ray Optics Model for the Optical Trapping Efficiency of Optical Tweezers［J］.Journal of the Korean Physical Society，2012，60(1):155-158.

［13］Timo A.Nieminen，Norman R.Heckenberg，and Halina Rubinsztein-Dunlop，Forces in optical tweezers with radially and azimuthally polarized trapping beams［J］.Optics Letters，2008，33(2):122-124.

［14］Masaki Michihata，Terutake Hayashi，and Yasuhiro Takaya，Measurement of axial and transverse trapping stiffness of optical tweezers in air using a radially polarized beam［J］.Applied Optics，2009，48(32):6143-6151.

［15］Yuichi Kozawa and Shunichi Sato，Optical trapping of micrometer-sized dielectric particles by cylindrical vector beams［J］.Optics Express，2010，18(10):10828-10833.