Efficient Mean Estimation in Log-normal Linear Models with First-order Correlated Errors

ZHANG SONGAND WANG DE-HUI

(1.Dalian Commodity Exchange,Dalian,Liaoning,116023) (2.School of Mathematics,Jilin University,Changchun,130012)

Efficient Mean Estimation in Log-normal Linear Models with First-order Correlated Errors

ZHANG SONG1,2AND WANG DE-HUI2,*

(1.Dalian Commodity Exchange,Dalian,Liaoning,116023) (2.School of Mathematics,Jilin University,Changchun,130012)

In this paper,we propose a log-normal linear model whose errors are fi rst-order correlated,and suggest a two-stage method for the efficient estimation of the conditional mean of the response variable at the original scale.We obtain two estimators which minimize the asymptotic mean squared error(MM)and the asymptotic bias(MB),respectively.Both the estimators are very easy to implement,and simulation studies show that they are perform better.

log-normal, fi rst-order correlated,maximum likelihood,two-stage estimation,mean squared error

1 Introduction

Log-normality is widely found in many f i elds from biology,medicine,insurance(see[1–3]), to geology,hydrology,environmentalology(see[4–6]),and so on.In these f i elds,researchers discover that linear models are often f i tted to the logarithmic transformed response variables very well,and these are the ordinary log-normal linear models,whose errors are independently and identically subject to N(0,σ2).The efficient mean estimation in the ordinary log-normal linear models has been considered by numbers of authors in the literature.Bradu and Mundlak[7]derived the uniformly minimum variance unbiased(UMVU)estimator and its variance.The maximum likelihood(ML)estimator and the restricted maximum likelihood(REML)estimator have also been used frequently in practice.A general discussion can be found in[8].Though the UMVU estimator has the smallest mean squared error(MSE) among all unbiased estimators,it may not have a smaller MSE than a biased estimator.Zhou[9]showed the fact that a biased conditionally minimal MSE estimator had smaller MSE than the UMVU estimator.El-shaarawi and Viveros[10]proposed a bias-corrected REML estimator,which was termed the EV estimator.More recently,Shen and Zhu[11]developed two estimators which minimize the asymptotic MSE and the asymptotic bias, respectively.

The ordinary log-normal linear models assume that the errors are i.i.d.However,in many practical cases,because of the time or spacial continuity of the response variables, the errors are correlated,which violates the i.i.d.assumption.If people ignore the violation and stick to use the ordinary log-normal linear models,it would result in large bias,and even wrong inference.Suppose that Z=(Z1,···,Zn)Tis the response vector,and xi= (1,xi1,···,xip)Tis the covariate vector for observation i.As f i rst-order correlation is the most common phenomena,we propose a log-normal linear model with f i rst-order correlated errors as follows:

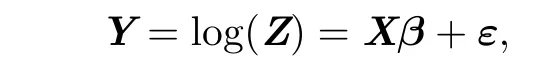
where

with

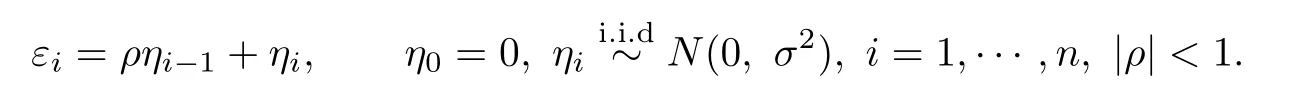
Then

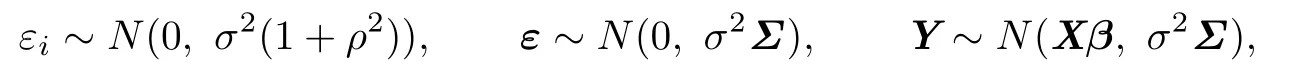
where

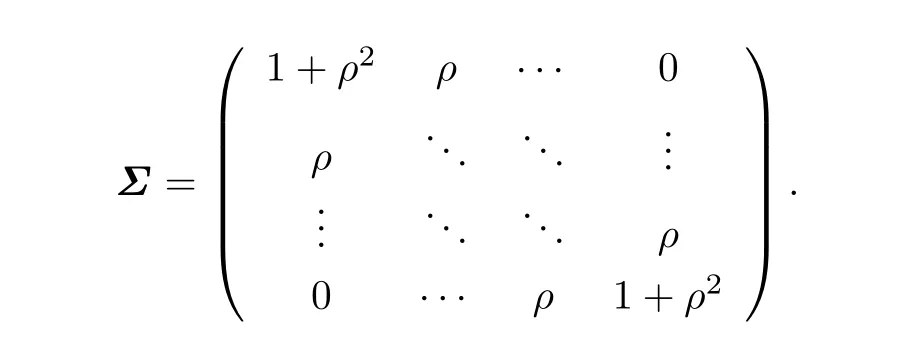
Apparently,if ρ=0,the model degenerates into the ordinary log-normal linear model.

In this paper,we focus on the efficient estimation of the conditional mean of Z0given x0,

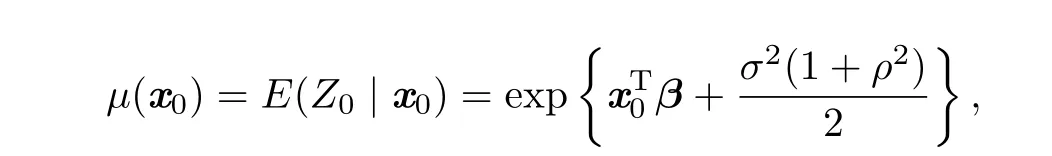
where x0is a new set of covariate values,

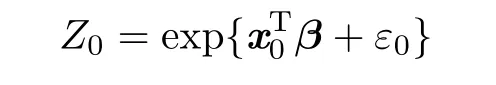
is the response variable at the original scale and ε0is the normal error with mean zero and variance σ2(1+ρ2).In Section 2,we derive the estimators ofµ(x0)and their MSE and bias when ρ is known.In Section 3,we suggest a moment method to estimate ρ and present its iterative algorithm,and thus,the estimators ofµ(x0)when ρ is unknown are obtained.In Section 4,we compare the MSE and bias of the estimators by simulation studies.

2 The Estimators ofµ(x0)when ρ Is Known

To better facilitate the following deduction,we give the next two propositions about the results of GLS estimator of β and the corresponding residual sum of squares(RSS)at f i rst.

Proposition 2.1[12]The GLS estimator for β is

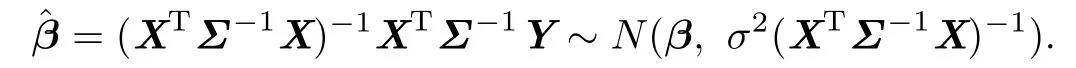
Proposition 2.2[12]Let m=n-(p+1).The residual sum of squares is

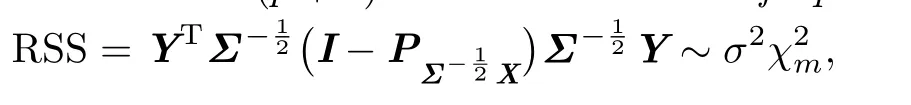
where

Remark 2.1Note that when rank(X)=p+1,the ML,GLS and REML estimators for β are identical.Furthermore,the REML and GLS estimators for σ2are the same,which is=RSS/m.The ML estimator for σ2is=RSS/n.

In the rest of this section,we derive two estimators from the following class of estimators:

which are the MM estimator

and the MB estimator

and they minimize the asymptotic MSE and bias,respectively.Note that both the ML and the REML estimators ofµ(x0)belong to this class.

Lemma 2.1Whenthe MSE ofis

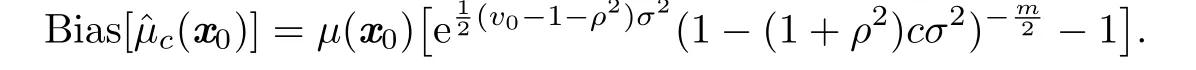
By Propositions 2.1 and 2.2,Lemma 2.1 can be easily proved.According to this lemma, we can see that the expression of MSE[ˆµc(x0)]is very complicated,and it is implausible to minimize it directly in this class.This leads us to consider minimizing its asymptotics.

Theorem 2.1Suppose thatThen

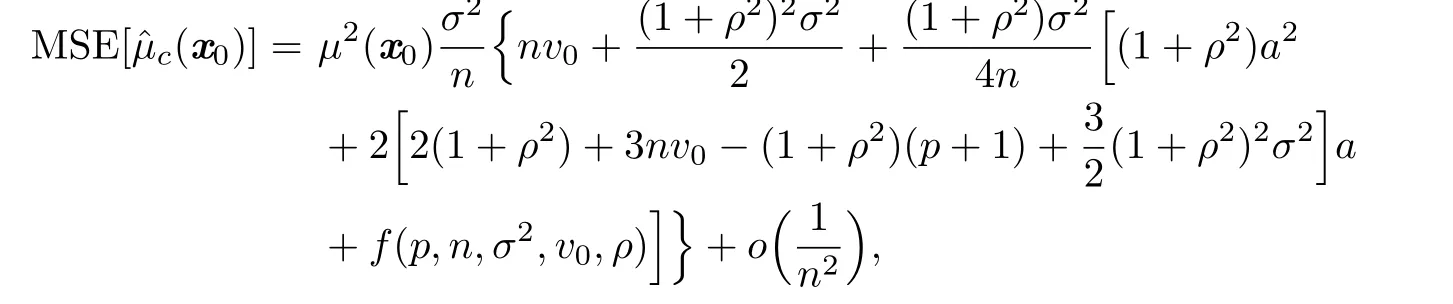
where

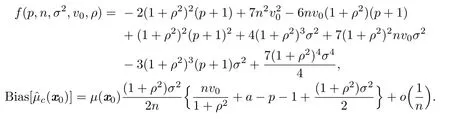
Proof.We f i rst note the following Taylor expansions

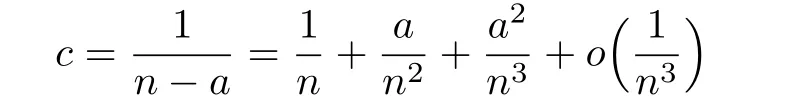
and

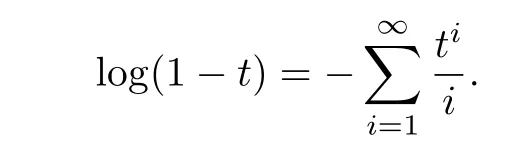
Def i ne

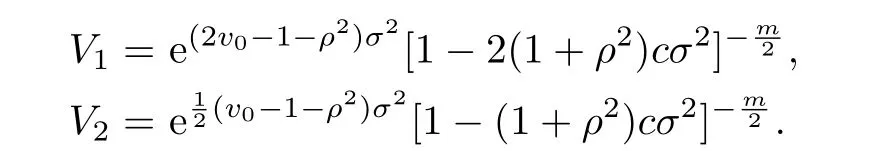
Expand V1and V2by using the above expansions,we have

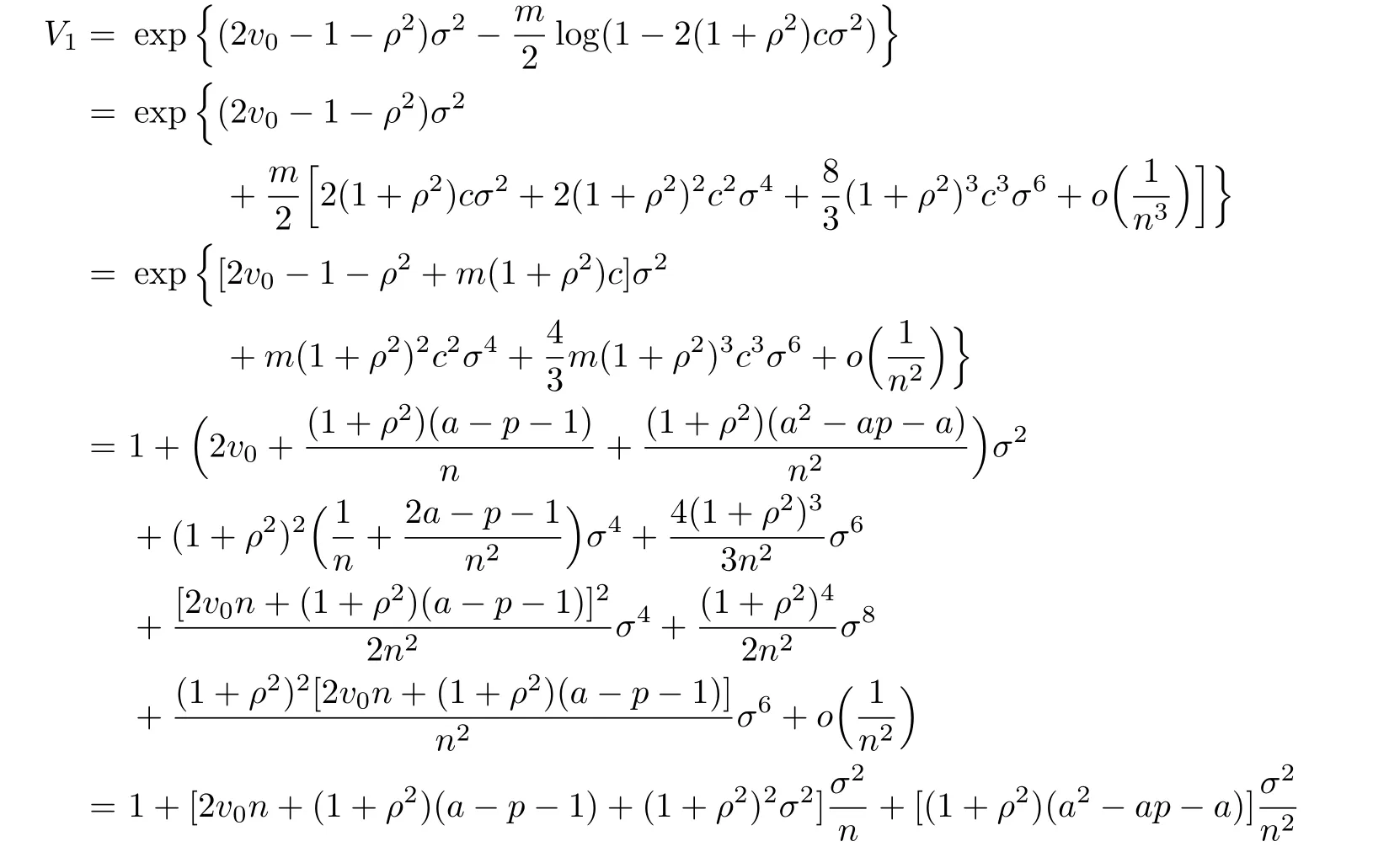
According to Lemma 2.1,we know that

which incorporate the above expressions for V1and V2,we obtain the result of MSEand BiasThis completes the proof.

We want to f i nd a constant c which can minimize the MSE up to the order ofTheorem 2.1 suggests us to f i nd a to minimize the following quadratic:

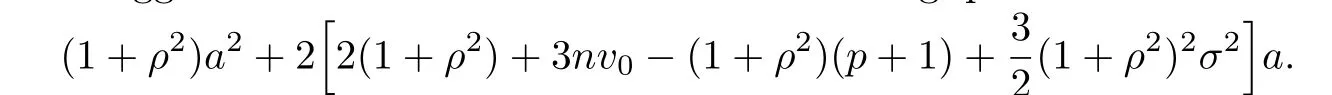
Obviously,the minimizer is

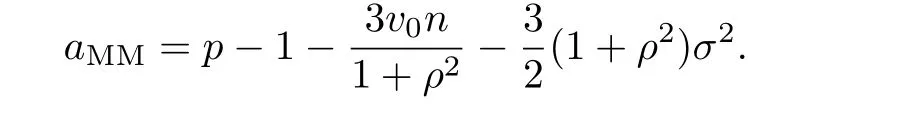
Thus,the constant c would beWhereas,in real applications,the true variance σ2is usually unknown.We propose to use its consistent estimator=RSS/m to replace it.Then,our proposed estimator is

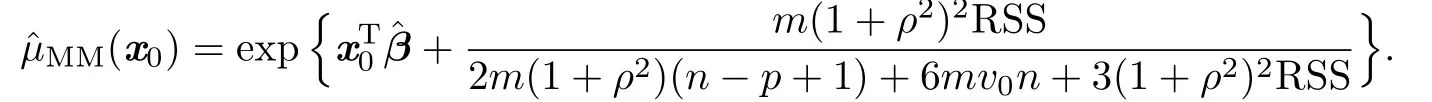
Similarly,to reduce the bias to the order of 1/n,Theorem 2.1 suggests to f i nd a to satisfy

which leads to

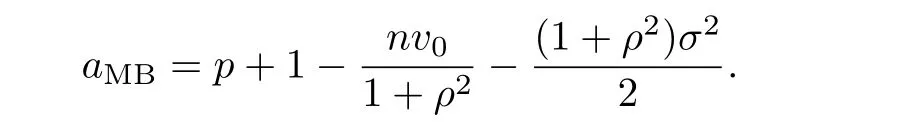
Therefore,the constant c would be

.Replacing σ2by,we obtain

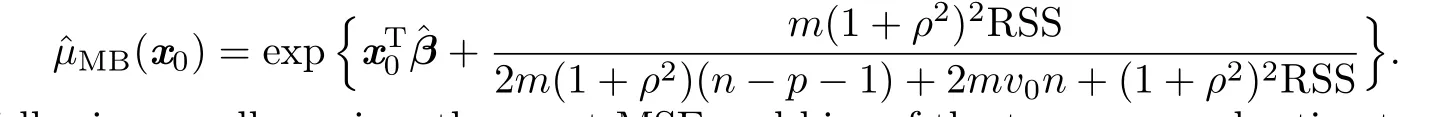
The following corollary gives the exact MSE and bias of the two proposed estimators.

Corollary 2.1Suppose that

Then

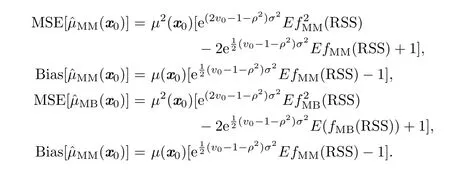
3 The Estimators ofµ(x0)when ρ Is Unknown

Firstly,we notice that the parameter ρ satisf i es the following equations: {

We propose a linear iterative algorithm to get the moment estimator of ρ.Start with a set of initial values of ρ and β,say ρ(0)and β(0)=[β0(0),β1(0),···,βp(0)]T,and letρ(j),β(j)=[β0(j),β1(j),···,βp(j)]Tand σ2(j)be the jth iterative results.According to(3.1)we obtain

Proceed(3.2)iteratively,and stop the iterative procedure when|ρ(j)-ρ(j-1)|＜δ,some preassigned tolerance limit.Take the jth result ρ(j)to be the moment estimator of ρ if it satisf i es

变系数Benjamin-Bona-Mahony-Burgers方程的微分不变量和精确解 李会会,刘希强,辛祥鹏(10-51)

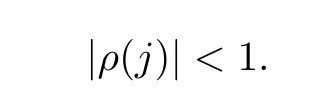
Otherwise,we need to change the initial values and repeat the procedures until we get the resonable result.This method can also be seen in[13].

We take the moment estimator ρ(j)to replace the known ρ in Section 2,and then obtain the estimators ofµ(x0)for the log-normal linear models with f i rst-order correlated errors when ρ is unknown.

4 Simulation Studies

In order to evaluate the performance of the MM and MB estimators,we simulate random samples from the log-normal linear models with f i rst-order correlated errors and compare the MSE and bias with the other estimators.Without loss of generality,we assume that there is only one covariate x,and it takes values between 0 and 1 uniformly.The regression coefficient vector β=(β0,β1)Tis taken to be(1,1)T,and the f i rst-order correlated coefficient ρ is taken in{0.5,0.8,1}.We consider the estimation ofµ(x0)for x0=(1,0.63),and present the results for the scenarios σ2=0.25 and sample size n∈{10,50,100}.

Tables 4.1 and 4.2 show the MSE and bias of ML,REML,UMVU,EV,MM and MB estimators when ρ is known,and Tables 4.3 and 4.4 show those when ρ is unknown.

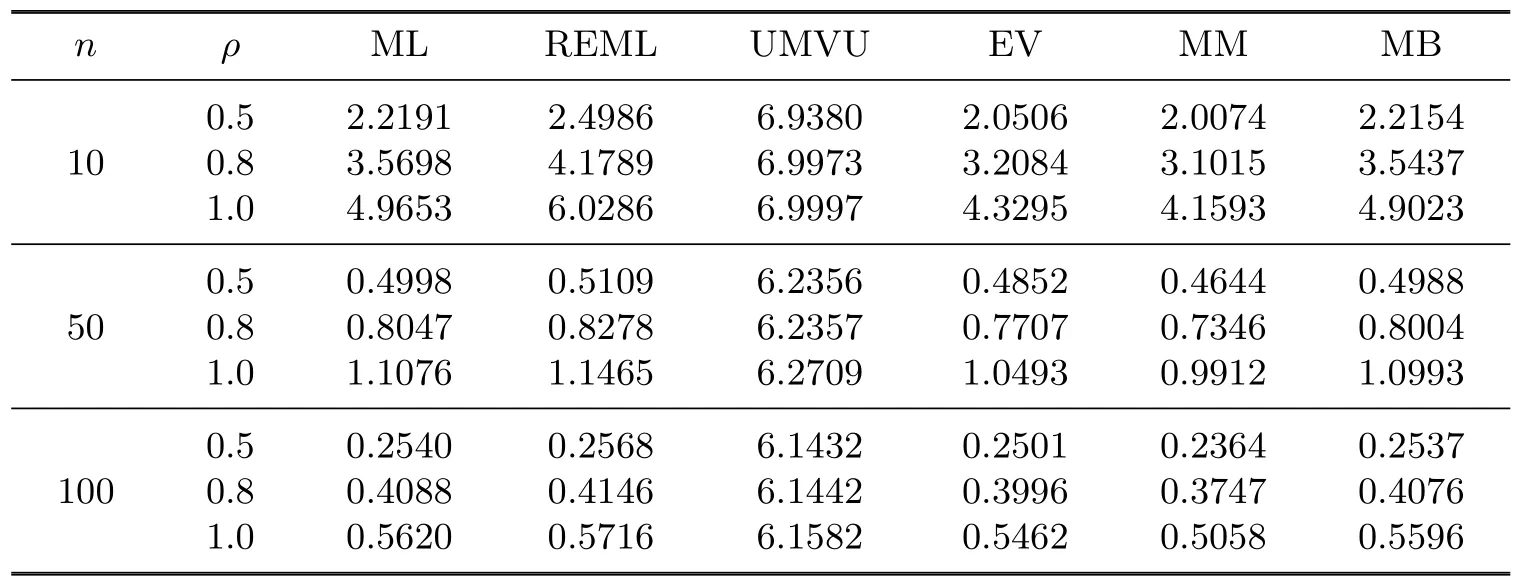
Table 4.1MSEs of the estimators when ρ is known

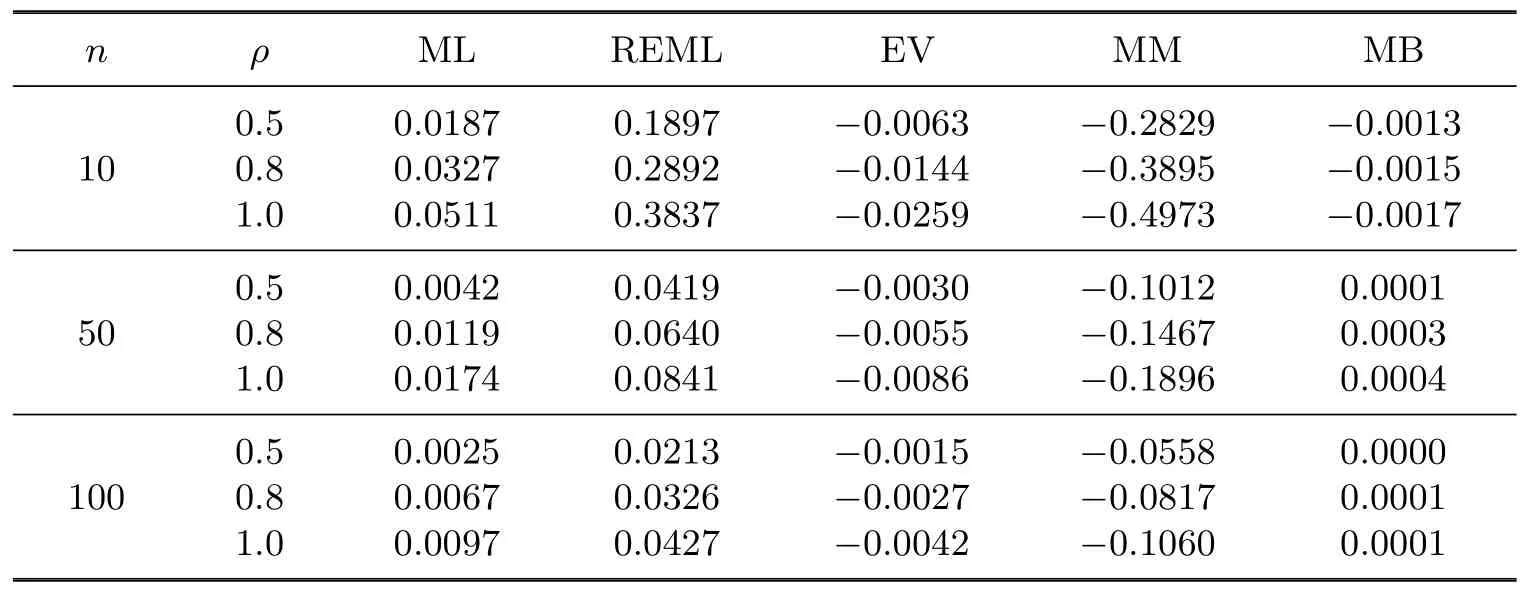
Table 4.2Bias of the estimators when ρ is known

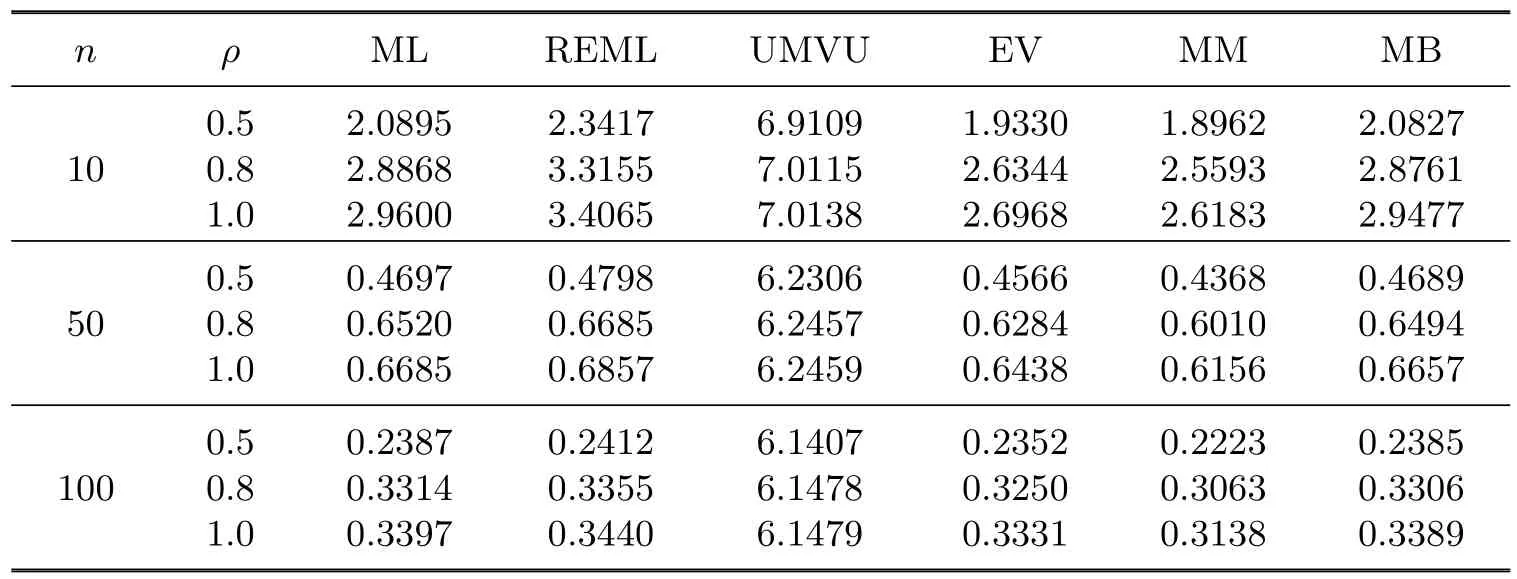
Table 4.3MSEs of the estimators when ρ is unknown

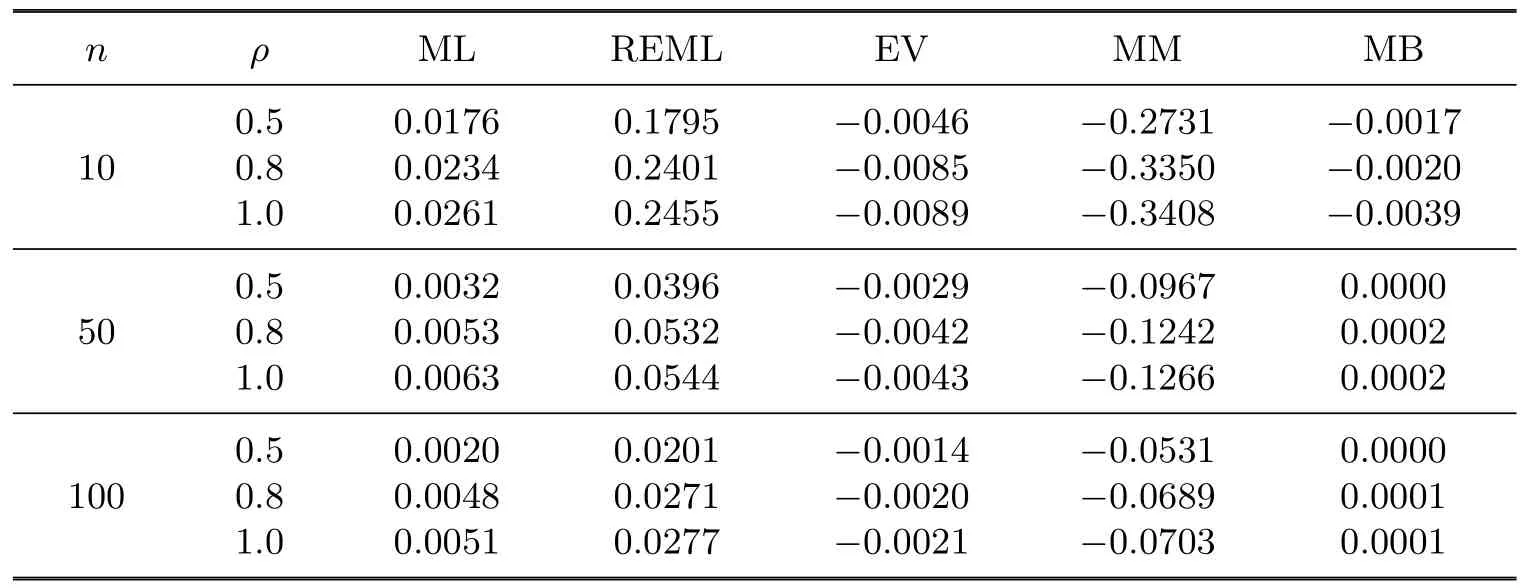
Table 4.4Bias of the estimators when ρ is unknown

The following observations are made from the tables:

1.For the MSE of the estimators,MM＜EV＜MB＜ML＜REML＜UMVU.

2.For the bias of the estimators,MB＜EV＜ML＜REML＜MM.

3.The MSE and the bias of the estimators are decreasing when n is growing.

4.The MSE and the bias of the estimators are growing when ρ is growing.

[1]Koch A L.The logarithm in biology 1.Mechanisms generating the log-normal distribution exactly.J.Theor.Biol.,1966,12(2):276–290.

[2]Shen H P,Brown L D,Zhi H.Efficient estimation of log-normal means with application to pharmacokinetic data.Statist.Med.,2006,25(17):3023–3038.

[3]Doray L G.UMVUE of the IBNR reserve in a lognormal linear regression model.Insurance Math.Econom.,1996,18(1):43–57.

[4]Cressie N.Block kriging for lognormal spatial processes.Math.Geol.,2006,38(4):413–443.

[5]Gilliom R J,Helsel D R.Estimation of distributional parameters for censored trace level water quality data estimation techniques.Water Resour.Res.,1986,22(2):135–146.

[6]Holland D M,De Oliveira V,Cox L H,Smith R L.Estimation of regional trends in sulfur dioxide over the eastern United States.Environmetrics,2000,11(4):373–393.

[7]Bradu D,Mundlak Y.Estimation in lognormal linear models.J.Amer.Statist.Assoc.,1970, 65(329):198–211.

[8]Lawless J F.Statistical Models and Methods for Lifetime Data.New York:Wiley,2002.

[9]Zhou X H.Estimation of the log-normal mean.Statist.Med.,1998,17(19):2251–2264.

[10]El-shaarawi A H,Viveros R.Inference about the mean in log-regression with environmental applications.Environmetrics,1997,8(5):569–582.

[11]Shen H P,Zhou Z Y.Efficient mean estimation in log-normal linear models.J.Statist.Plann. Inference,2008,138(3):552–567.

[12]Wang S G,Shi J H,Yin S J,Wu M X.An Introduction of Linear Model.Beijing:Science Press,2005.

[13]He S Y.Applied Time Series Analysis.Beijing:Peking Univ.Press,2003.

A

1674-5647(2013)03-0271-09

Received date:Nov.22,2011.

The NSF(11271155)of China and Research Fund(20070183023)for the Doctoral Program of Higher Education.

*Corresponding author.

E-mail address:sngchng@gmail.com(Zhang S),wangdh@jlu.edu.cn(Wang D H).

2000 MR subject classi fi cation:62J12,62M10,62F10