The Centres of Gravity of Periodic Orbits

SUN ZHE AND HOU BING-ZHE

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Lei Feng-chun

The Centres of Gravity of Periodic Orbits

SUN ZHE AND HOU BING-ZHE*

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Lei Feng-chun

Let f:I→I be a continuous map.If P(n,f)={x∈I;fn(x)=x} is a f i nite set for each n∈N,then there exits an anticentered map topologically conjugate to f,which partially answers a question of Kolyada and Snoha.Specially, there exits an anticentered map topologically conjugate to the standard tent map.

periodic orbit,centre of gravity,anticentered map,tent map

1 Introduction

Let(X,ρ)be a compact metric space and f:X→X a continuous map.(X,f)is called a discrete dynamical system.The main task is to investigate how the points of X move,i.e., to understand the“orbits”.For x∈X,the orbit of x under f is

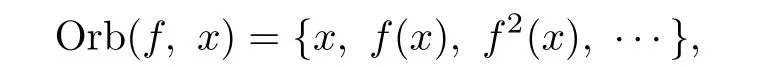
where fn=f◦f◦···◦f is the nth iteration of f obtained by composing f with itself n times.Periodic orbit is a simple type of orbit.If there exists a positive integer n such that fn(x)=x,then x∈X is called a periodic point and n is called a period of x.Furthermore, denote

Let I=[0,1].The dynamical systems on I have been well studied(see[1–2]).With regards to periodic points,there are also many results such as Sarkovskii's theorem(see [3–4]).In this article,we are interested in some properties of periodic orbits in dynamical systems(I,f).

For a periodic point x of period p in a dynamical system(I,f),is said to be the centre of gravity of the orbit of x.A map f:I→I is said to be centered if the map x→γf(x)is a constant on the set of periodic points,i.e.,each periodic orbit of f has the same centre of gravity;and f is said to be anticentered if any two dif f erent periodic orbits of f must have dif f erent centre of gravity.

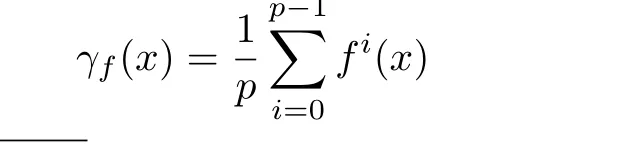
Recall that a map F:X×I→X×I is called triangular(or skew product)if it has the form of

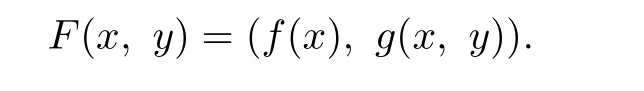
In the research of these maps,ones are interested in the standard tent map τ:I→I,

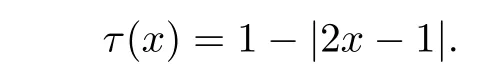
S.Kolyada and L.Snoha asked whether the standard tent map is anticentered,which was motivated by some results from[5].M.Misiurewicz investigated that it is not anticentered since 22/127 and 26/127 belong to dif f erent periodic orbits of period 7 with the same centre of gravity 72/127(see[6]).Furthermore,they asked the following question in[6].

Question ALet f:I→I be a continuous map.Can one always topologically conjugate f to an anticentered map g:I→I?

We give a positive answer to Question A for the standard tent map.In fact,it holds for a special class of interval self-maps which contains the standard tent map.

Theorem 1.1Let f:I→I be a continuous map.If P(n,f)={x∈I;fn(x)=x}is a f i nite set for each n∈N,then there exists an anticentered map g:I→I topologically conjugate to f.

Corollary 1.1Let τ be the standard tent map.Then there exists an anticentered map g:I→I topologically conjugate to τ.

Proof.Since P(n,τ)is a f i nite set for each n∈N,it is easy to get this conclusion by Theorem 1.1.

2 Preliminaries

In this section,we make some necessary preparation for proving Theorem 1.1.First of all, let us review some def i nitions and conclusions in topology(see[7]).

Let X and Y be two metric spaces.C(X,Y)denotes the set of all continuous functions from X to Y.The metric dYon Y introduces a metric d on C(X,Y)for all f,g∈C(X,Y):

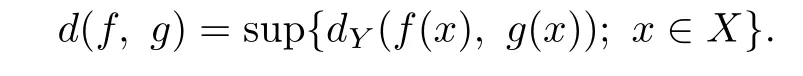
Denote

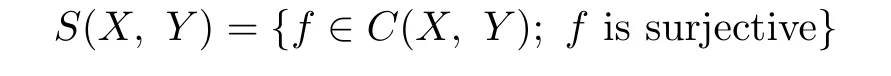
and by H(X)the autohomeomorphism group of X.

Def i nition 2.1Let X and Y be two metric spaces with X compact and∊＞0.A function f∈C(X,Y)is called an∊-map if for every y∈Y,

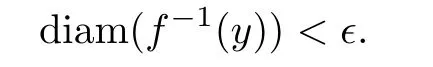
Put

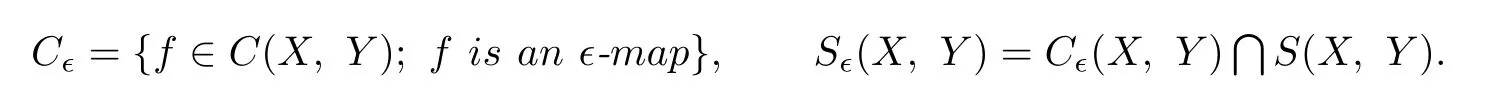
In addition,denote

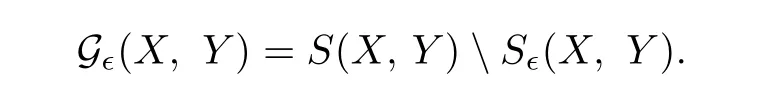
Theorem 2.1(The Inductive Convergence Criterion)Let X be a compact metric space, and{hn}na sequence in H(X)such that for all n∈N,

Now,we def i ne a type of perturbations to a orientation-preserving homeomorphism on I.A homeomorphism f on I is called orientation-preserving if f(x)＞f(y)when x＞y.

Def i nition 2.2Let f:I→I be an orientation-preserving homeomorphism,and let,k∈N.Suppose that Ji=[ai,bi]is a closed neighborhood of ci,are pair disjoint,and Si∈(f(ai),f(bi)).Def i ne g:I→I by

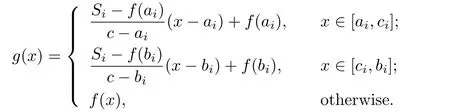
The map g is called an angle-perturbation of f from f(ci)to Sion Ji.Specially,when f is the identity map,g is called an angle-perturbation from cito Sion Ji.

Remark 2.1It is not difficult to see that for every orientation-preserving homeomorphism f:I→I,the angle-perturbation g def i ned as above is also an orientation-preserving homeomorphism.Moreover,An angle-perturbation may be seen as Fig.2.1.

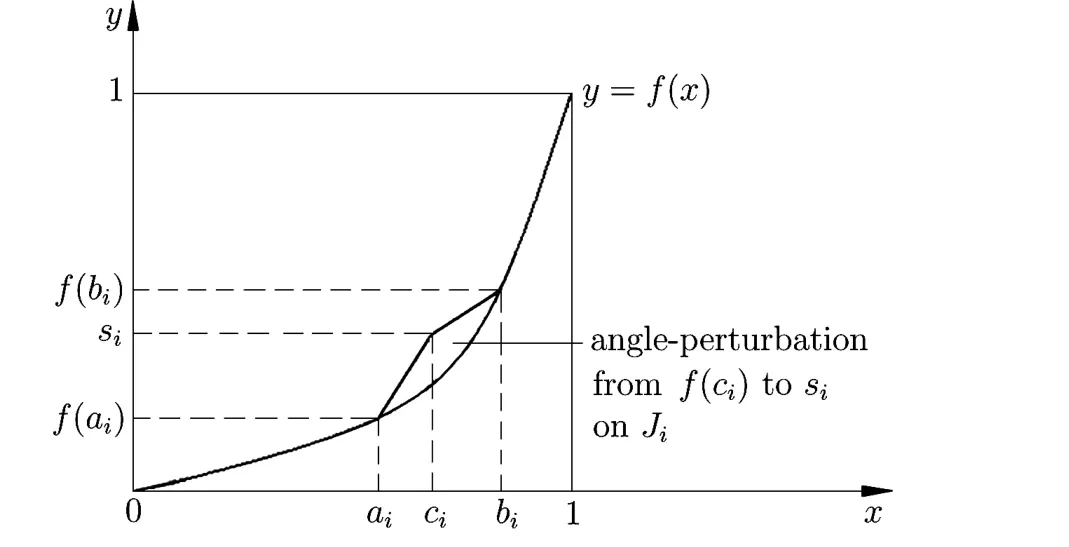
Fig.2.1

Moreover,one can obtain the following result.

Lemma 2.1Let f:I→I be an orientation-preserving homeomorphism and∈int(I).For any∊＞0,there exists a closed neighborhood Ji=[ai,bi]of ciand Si∈(f(ai),f(bi))such that the angle-perturbation g from f(ci)to Sion Jisatisf i es d(g,f)＜∊. Proof.Given any∊＞0,by the uniform continuity of f,for each ci,there exists a closed neighborhood Ji=[ai,bi]of cisuch thatare pair disjoint and

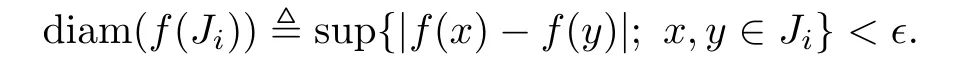
Then for any Si∈(f(ai),f(bi)),the angle-perturbation g from f(ci)to Sion Ji,satisf i es d(g,f)＜∊.

3 The Proof of Theorem 1.1

Proof of Theorem 1.1Let a sequence of homeomorphismsfrom I to itself be given.For each i∈N,denote

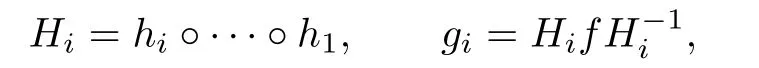
and

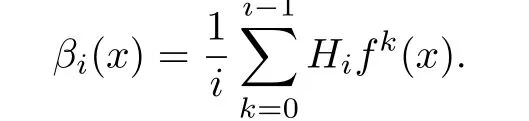
Our aim is to construct a sequence of homeomorphismssuch that for every i∈N the following conditions are satisf i ed:

(b)For any s,t＜i,if x∈P(s,f)and y∈P(t,f)are two periodic points in distinct periodic orbits,then βs(x)/=βt(y);

(c)d(hi,id)is small enough to satisfy the conditions of Theorem 2.1,where id denotes the identity map on I.

Let h1=H1=id.Obviously it satisf i es conditions(a)and(c).

For any distinct x,y∈P(1,f),we also have β1(x)=x/=y=β1(y),which implies condition(b).

Now suppose that we have obtained homeomorphismssatisfying conditions(a)–(c).

Consider P(n+1,f).Let

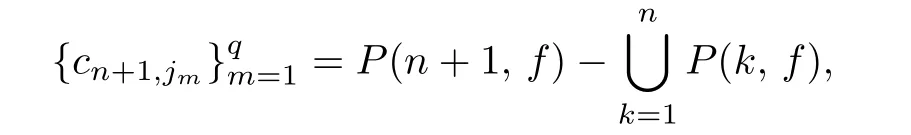
where q is the number of points in

According to Lemma 2.1,the f i niteness of q and,we can choose Jn+1,jmas the closed neighborhood ofsuch thatare pair disjoint and

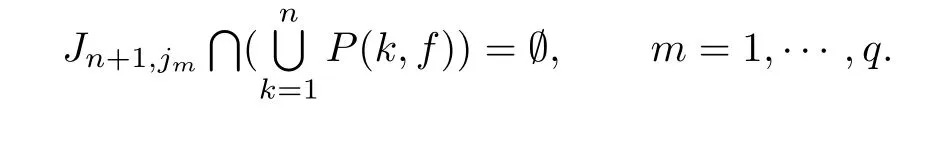
Then there exists an angle-perturbation hn+1from f(cn+1,jm)to some Sn+1,jm∈Jn+1,jmon Jn+1,jmsatisfying

(2)d(hn+1,id)is small enough to satisfy the conditions of Theorem 2.1.

Continuing in this manner,we obtain a sequence of homeomorphismswhich satisfy conditions(a)–(c)obviously.

By Theorem 2.1 and the condition(c),is a homeomorphism from I onto itself.Let g=hfh-1.By condition(a),we have

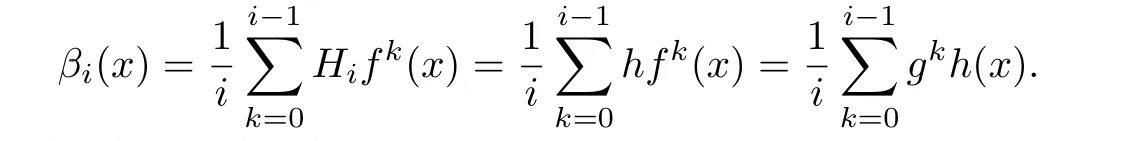
Notice that h:P(i,f)→P(i,g)is bijective for each i∈N.Thus,by the condition(b),g is an anticentered map topologically conjugate to f.

[1]Coppel W A.Continuous Maps of an Interval.Mathematical Sciences Research Centre:Lecture Notes in Australian National University,1984.

[2]Block L S,Coppel W A.Dynamics in one dimension:Lecture Notes in Mathematics,1513. Berlin:Springer-Verlag,1992.

[3]Sarkovskii A N.Coexistence of cycles of a continuous mapping of the line into itself(in Russian). Ukrain.Math.Zh.,1964,16:61–67.

[4]Sarkovskii A N.On cycles and the structure of a continuous mapping(in Russian).Ukrain. Math.Zh.,1965,17:104–111.

[5]Alseda L,Kolyada S,Llibre J,Snoha L’.Entropy and periodic points for transitive maps.Trans. Amer.Math.Soc.,1999,351:1551–1573.

[6]Kolyada S,Snoha L’.Entropy,periodic points and transitivity of maps.Available at http://www.math.iupui.edu/˜mmisiure/open/,Oct.26,2002.

[7]von Mill J.Inf i nite-Dimensional Topology,Prerequisites and Introduction.Amsterdam:North-Holland,1989.

A

1674-5647(2013)03-0239-05

Received date:April 18,2011.

The Undergraduates Innovating Experimentation Project(2010C31048)of Jilin University.

*Corresponding author.

E-mail address:jiji6454@sina.com(Sun Z),houbz@jlu.edu.cn(Hou B Z).

2000 MR subject classif i cation:37E05