The Supersolvable Order of Hyperplanes of an Arrangement

GAO RUI-MEIAND PEI DONG-HE

(1.College of Science,Changchun University of Science and Technology,Changchun,130022) (2.School of Mathematics and Statistics,Northeast Normal University,Changchun,130024)

Communicated by Du Xian-kun

The Supersolvable Order of Hyperplanes of an Arrangement

GAO RUI-MEI1AND PEI DONG-HE2

(1.College of Science,Changchun University of Science and Technology,Changchun,130022) (2.School of Mathematics and Statistics,Northeast Normal University,Changchun,130024)

Communicated by Du Xian-kun

This paper mainly gives a sufficient and necessary condition for an order of hyperplanes of a graphic arrangement being supersolvable.In addition,we give the relations between the set of supersolvable orders of hyperplanes and the set of quadratic orders of hyperplanes for a supersolvable arrangement.

quadratic arrangement,graphic arrangement,supersolvable order of hyperplane,quadratic order of hyperplane,supersolvable order of vertices

1 Introduction

As we know,a central question in the theory of hyperplane arrangements is the problem of expressing topological invariants of the complement space in terms of combinatorics.Therefore,the study of arrangements with rational K[π,1]complements has a relatively long history(see[1–3]).Assume that M(A)is the complement of the arrangement A.Then a necessary condition for M(A)being rational K[π,1]is that the Orlik-Solomon algebra A(A)is quadratic(see[4–5]).Therefore,the study of quadratic Orlik-Solomon algebras attracts more and more attentions(see[6]).Pearson[7]gave the def i nition of a quadratic arrangement,and showed that if A is a quadratic arrangement,then its Orlik-Solomon algebra A(A)is quadratic.Hence,it is important to study quadratic arrangements. It was pointed out in[8]that if A is a supersolvable arrangement,then A is a quadratic arrangement under some supersolvable order of hyperplanes.A natural question is whether there exists a good method to characterize all the supersolvable orders of hyperplanes for a supersolvable arrangement,and what is the relation between the supersolvable order ofhyperplanes and the order which makes A quadratic.We give the answers of these two questions in this paper.

Firstly,this paper gives a sufficient and necessary condition of an order of hyperplanes of a graphic arrangement being supersolvable.Secondly,we prove that the set of the supersolvable orders of hyperplanes is strictly contained in the set of quadratic orders of hyperplanes for any supersolvable arrangement.

We assume that A is a central arrangement in this paper.

2 Basic Notions

Let K be a f i eld and V be a vector space of dimension n on K.A hyperplane H in V is an affine subspace of dimension(n-1).A hyperplane arrangement A is a f i nite set of hyperplanes in V.Most often we take K=R.We simply use the term arrangement for a hyperplane arrangement.We call A central ifH=T/=Ø.Let L=L(A)be the set of nonempty intersections of hyperplanes in A.Def i ne X≤Y in L if X⊇Y.In other words, L is partially ordered by reverse inclusion.We call L the intersection poset of A.Let X∨Y be the least upper bound of X and Y,and X∧Y be the greatest lower bound of X and Y.For any X∈L,the rank of X is given by r(X)=codim(X).A pair(X,Y)∈L×L is called a modular pair if

An element X∈L is called a modular element if(X,Y)is a modular pair for all Y∈L. We call A supersolvable if L(A)has a maximal chain of modular elements

where r=r(T).

We introduce an arbitrary linear order“≺”on the hyperplanes of A,that is,Hi≺Hjif 1≤i＜j≤|A|.

Let A be a supersolvable arrangement with order≺.We say that the order≺is a supersolvable order of hyperplanes if there exists a maximal modular chain

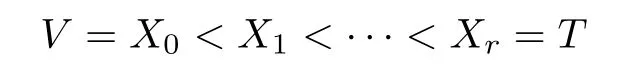
in L such that

(1)X1=H1;

(2)for 1＜i≤r,there exists ni≥2 such that

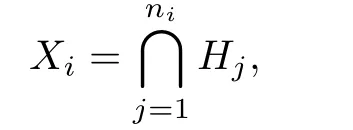
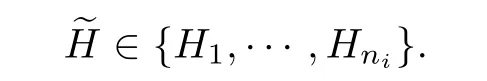
We denote by≺sa supersolvable order of hyperplanes.

Let S=(Hi1,···,Hip)be a p tuple of A.We say that an S is dependent if r(∩S)＜|S|, otherwise,an S is independent.A p-tuple is a circuit if it is minimally dependent.We calla p-tuple S=(Hi1,···,Hip)standard if Hi1≺···≺Hip.A standard p-tuple S is a broken circuit if there exists H∈A such that H≺minS and(H,S)is a circuit.Let

We call BC the broken circuit set of A.We say that A is a quadratic arrangement with respect to linear order≺,if for any S∈BC,there exists T∈BC with T⊆S and|T|=2. At this time,we call the order≺a quadratic order of hyperplanes.

Let G=(V(G),E(G))be a simple graph with n vertices,where V(G)is the set of vertices of G,and E(G)is the set of edges of G.We def i ne

to be the graphic arrangement corresponding to G.It is well known that G is a chordal graph if and only if A(G)is supersolvable.

A graph G with at least one edge is doubly connected if it is connected and remains connected upon the removal of any vertex(and all incident edges).We suppose that G is doubly connected in this paper.

The symbols and notions in this paper are the same as the ones in[9–10].

3 A Sufficient and Necessary Condition for the Supersolvable Order of Hyperplanes

The following lemma gives a sufficiency and necessity condition for a graphic arrangement being supersolvable.

Lemma 3.1[11]Let G be a simple graph with n vertices.Its corresponding graphic arrangement A(G)is supersolvable if and only if the vertices of G can be labeled as 1,2,···,n, such that if i＜k,j＜k and(i,k),(j,k)∈E(G),then(i,j)∈E(G).

Remark 3.1We call the order of vertices which satisf i es the condition in Lemma 3.1 a supersolvable order of vertices of G.As we know,any order of vertices of G can be regarded as a permutation σ=a1a2···an∈Snof n elements,where

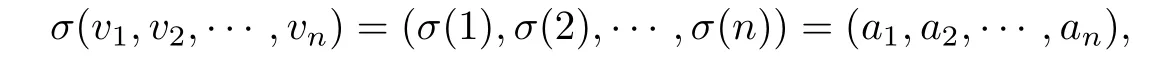
with ai∈[n]={1,2,···,n},1≤i≤n,and the Snis the permutation group of n elements.

Def i nition 3.1Assume that σ1,σ2are two dif f erent orders of vertices of G.We def i ne σ1～σ2if σ1and σ2satisfy the following two conditions:

(1)there exist 1≤i,j≤n such that σ1(vi)=σ2(vj)=1,and σ1(vj)=σ2(vi)=2;

(2)σ1(vk)=σ2(vk),if k/=i,j.

Proposition 3.1Assume that G is a chordal graph with n vertices.In the set of supersolvable orders of vertices of G,we identify σ1with σ2if σ1～σ2.Then there exists a one-to-one correspondence between the set of supersolvable orders of vertices of G and the set of maximal modular chains in L(A(G)).

Proof.First,we prove that if σ is a supersolvable order of vertices of G,then(1,2)∈E(G)σ,where E(G)σdenotes the set of edges of G after labeling all the vertices of G with respect to σ.This conclusion can be proved by induction on|V(G)|.Since G is doubly connected,the conclusion is clear for the case|V(G)|=3.When|V(G)|=p,let Gi=(V(Gi),E(Gi)),where

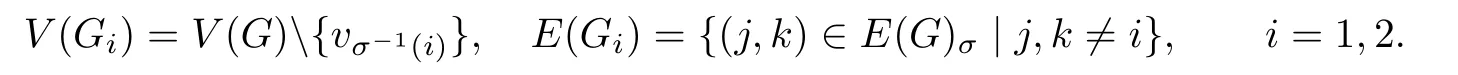
Then by the induction hypothesis,(2,3)∈E(G1),(1,3)∈E(G2).Hence,

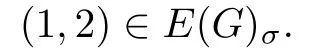
For any f i xed 1≤i≤n,let

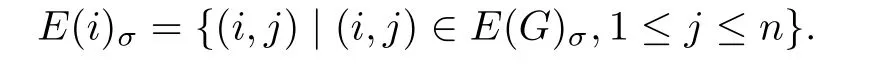
Def i ne a mapping

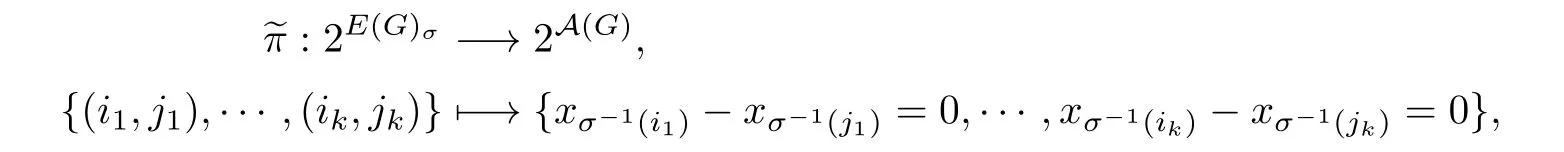
where 1≤ip,jp≤n,and ip/=jp,1≤p≤k. Let

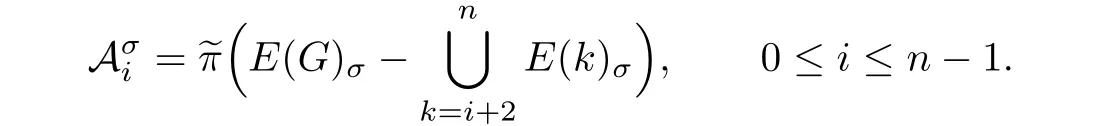
Since(1,2)∈E(G)σ,we have

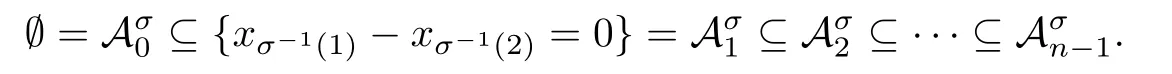
Let

Then by the proof of Lemma 3.1 in[11],is a modular element in L(A(G)).We use the symbol Cσto denote the following maximal modular chain:

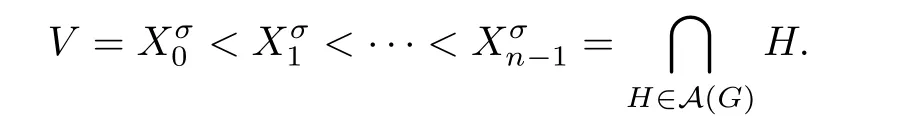
Def i ne a mapping from the set of supersolvable orders of vertices of G to the set of maximal modular chains in L(A(G))as follows:

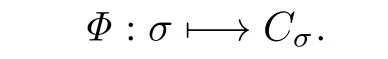
Since we identify σ1with σ2if σ1～σ2,it is clear that the mapping Φ is injective. Assume that we have a maximal modular chain∩

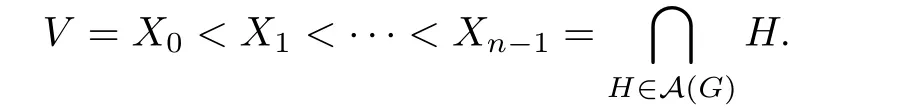
Since Xi(0≤i≤n-1)is a modular element,we can label the vertices viand vjby 1 and 2,respectively,if X1={xi-xj=0}.Also,we can label other vertices by the integers from 3 to n according to the elements from X2to Xn-1,respectively,and the order of vertices with respect to this labeling is a supersolvable order of vertices.Therefore,we can say that the mapping Φ is surjective.This completes the proof.

If G is a chordal graph,then it has the supersolvable order of vertices,and its corresponding arrangement A(G)has the supersolvable order of hyperplanes.Do they have somerelations?Next,we give a conclusion about them.First of all,if σ is an order of vertices of G,we def i ne its corresponding order of edges τσ.In order to do this,we give the def i nitions of some symbols.

For a graph G with n vertices,we assume that the order of vertices σ is f i xed.

Let

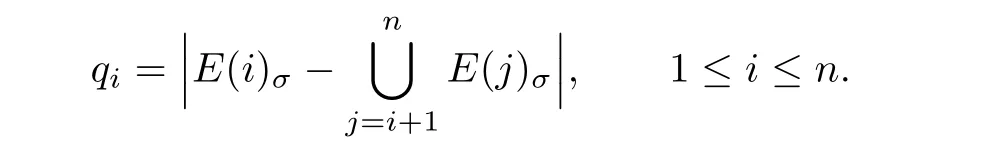
For σ,we def i ne its corresponding order of edges

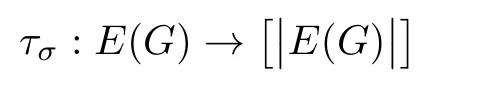
as follows:

For any edge

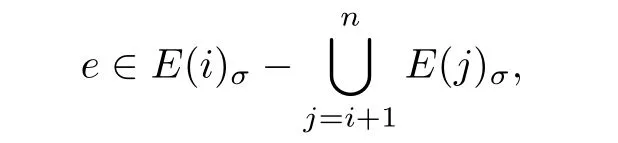
τσsatisf i es

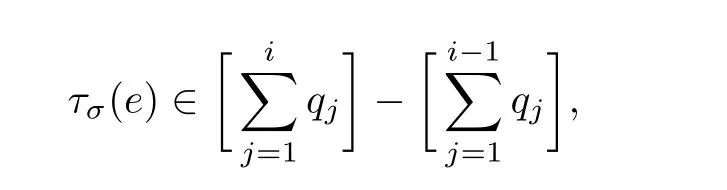
and dif f erent edges have dif f erent images,where 2≤i≤n. Since

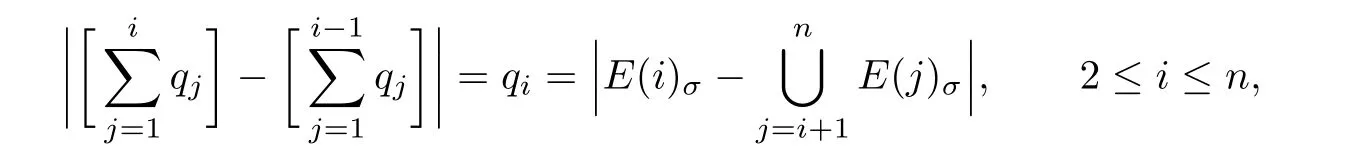
we know that τσis a bijection between E(G)andE(G).

From the def i nition of τσ,it is clear that there are many orders of edges correspond to σ,and the number of τσis

As we know,there exists a canonical bijection between E(G)and A(G).Therefore,for any τσ,the order of edges which corresponds to σ,there exists an order of hyperplanes ofnaturally,and we may also write it as τσ.From now on,we do not distinguish the orders of edges of G and the orders of hyperplanes of A(G).

Theorem 3.1If G is a chordal graph,then

Proof.If σ is a supersolvable order of vertices of G,we consider the maximal modular chain decided by σ,

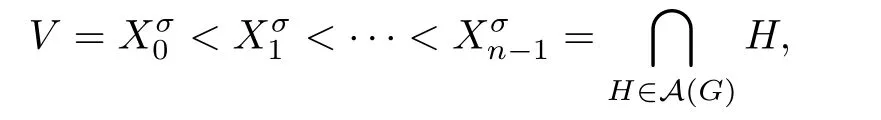
where

Then

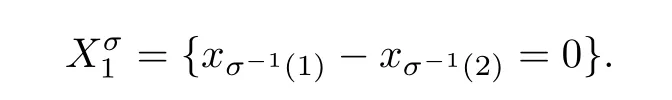
And for

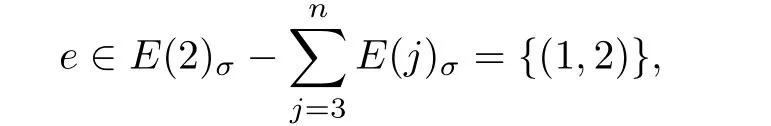
we have τσ(e)∈[1],that is,

In addition,for i＞1,

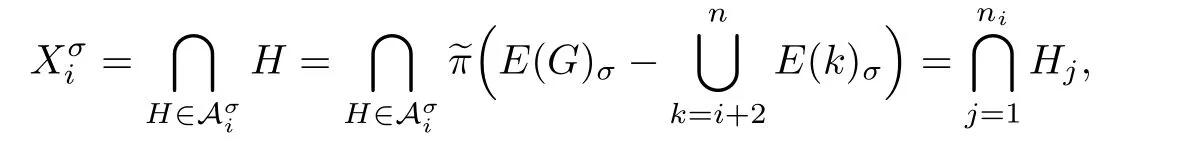
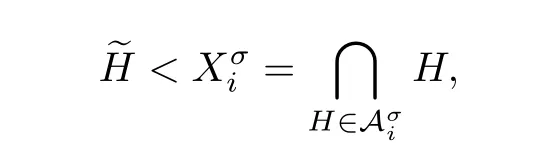
then

Hence

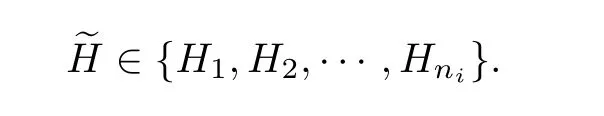
Conversely,for any supersolvable order of hyperplanes of A(G)≺s,it decides a unique maximal modular chain in L(A(G))as follows:

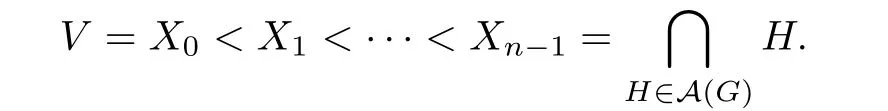
By Proposition 3.1,there exists a supersolvable order of vertices σ,which satisf i es

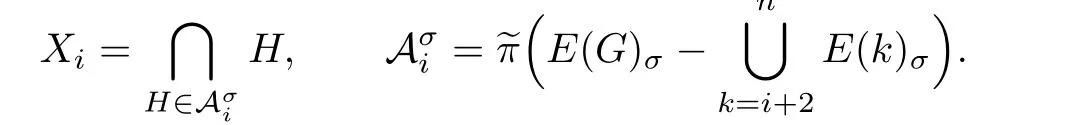
Next,we prove that≺sis an order of edges of E(G)which corresponds to σ. Since≺sis a supersolvable order of hyperplanes of A(G),one has

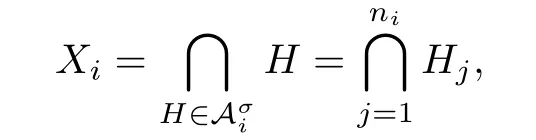
and

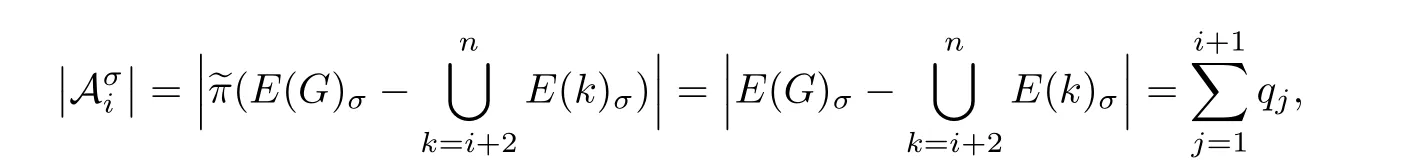
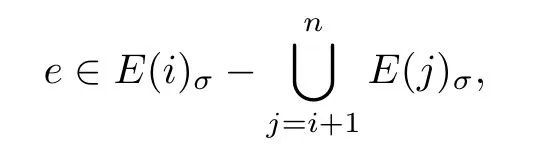
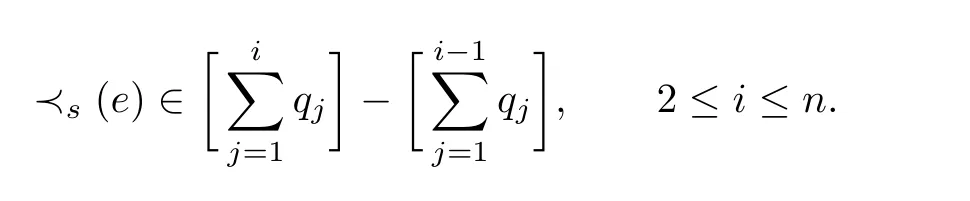
it satisf i esTherefore,≺sis an order of edges of E(G)which corresponds to σ.This completes the proof.

4 The Relations Between the Set of Supersolvable Orders of Hyperplanes and the Set of Quadratic Orders of Hyperplanes

In this section,we mainly give the conclusion that the set of the supersolvable orders of hyperplanes is strictly contained in the set of quadratic orders of hyperplanes for any supersolvable arrangement.

Theorem 4.1Let A be a supersolvable arrangement.If≺sis a supersolvable order of hyperplanes respects to the maximal modular chain

then≺smust be a quadratic order of hyperplanes of A.

Proof.Suppose that S=(Ha,Hb,Hc)is a minimally broken circuit with respect to the order≺s,and

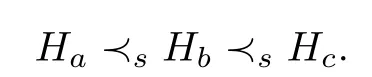
Let

Then there exist i1,i2,i3with 1≤i1≤i2≤i3≤r such that

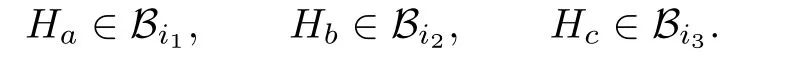
We can get the conclusion that i1,i2,i3are pairwise distinct.Otherwise,we assume that j=i1=i2since i1,i2,i3cannot be equal.Let Y=Ha∨Hb.By the property of modular element X,we obtain

Then there exists a hyperplane Ht≤Xj-1such that S1=(Ht,Ha,Hb)is dependent.Therefore T=(Ha,Hb)is a broken circuit.This contradicts the minimality of S=(Ha,Hb,Hc). Since S=(Ha,Hb,Hc)is a broken circuit,there exists a hyperplane Hp≺sHasuch that

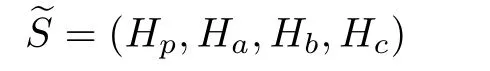
is a circuit.By the def i nition of≺s,we can see

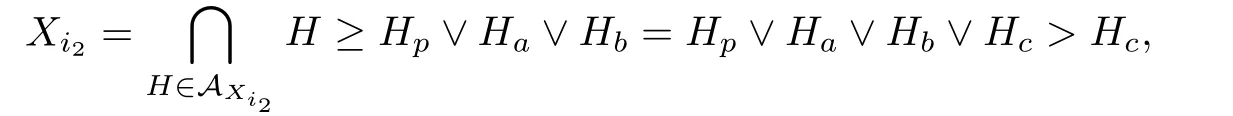
which is a contradiction.

If

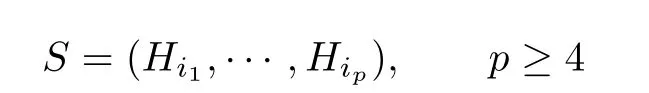
is a minimally broken circuit,we can also get a contradiction by using of the same method. Therefore,the broken circuit set has only 2-broken circuits.We complete the proof.

Next,we give an example of a quadratic arrangement under an order which is not a supersolvable order of hyperplanes.

Example 4.1The corresponding graphic arrangement A(G)of the following graph G is a quadratic arrangement under the order given in Fig.4.1.It is also easy to see this order is not a supersolvable order of hyperplanes.

Fig.4.1A quadratic arrangement under a non-supersolvable order of hyperplanes

[1]Falk M,Randell R.The lower central series of a f i ber-type arrangements.Invent.Math.,1985, 82:77–88.

[2]Falk M.The minimal model of the complement of an arrangement of hyperplanes.Trans. Amer.Math.Soc.,1988,309:543–556.

[3]Kohno T.Sˊerie de Poincarˊe-Koszul associˊee aux groupes de tresses pures.Invent.Math.,1985, 82:57–75.

[4]Falk M.Line-closed matroids,quadratic algebras,and formal arrangements.Adv.in Appl. Math.,2002,28:250–271.

[5]Papadima S,Yuzvinsky S.On rational K[π,1]spaces and Koszul algebras.J.Pure Appl. Algebra,1999,144:157–167.

[6]Yuzvinsky S.Orlik Solomon algebras in algebra and topology.Russian Math.Surveys,2001, 56:87–166.

[7]Pearson K J.Cohomology of OS algebras for quadratic arrangements.Lect.Mat.,2002,22: 103–134.

[8]Bj¨orner A,Ziegler G.Broken circuit complexes:factorization and generalizations.J.Combin. Theory Ser.B,1991,5:96–126.

[9]Orlik P,Terao H.Arrangements of Hyperplanes.Berlin:Springer-Verlag,1992.

[10]Stanley R P.An Introduction to Hyperplane Arrangements.In:Miller E,Reiner V,Sturmfels B.Geometric Combinatorics.Providence,RI:IAS/Park City Math.Ser.Amer.Math.Soc., 2004,13:389–496.

[11]Stanley R P.Supersolvable lattices.Algebra Universalis,1972,2:197–217.

A

1674-5647(2013)03-0231-08

Received date:March 18,2011.

The NSF(10871035)of China.

E-mail address:gaorm135@nenu.edu.cn(Gao R M).

2000 MR subject classif i cation:32S22,52C35