An Evolving Random Network and Its Asymptotic Structure

LI ZHI-MIN AND GENG JIN-HUI

(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu,Anhui,241000)

Communicated by Wang De-hui

An Evolving Random Network and Its Asymptotic Structure

LI ZHI-MIN AND GENG JIN-HUI

(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu,Anhui,241000)

Communicated by Wang De-hui

In this paper,we propose an evolving random network.The model is a linear combination of preferential attachment model and uniform model.We show that scaling limit distribution of the number of leaves at time n is approximated by nomal distribution and the proportional degree sequence obeys power law.The branching structure and maximum degree are also discussed in this paper.

random network,scale-free graph,degree sequence

1 Introduction

In the recent ten years,there has been much interest in understanding the properties of real large-scale complex networks which describe a wide range of systems in nature and society such as the internet,the world wide web,protein interaction networks,brain cell networks, science collaboration graph,web of human sexual contact,phone-call networks,power and neural networks,etc.(see[1]).In pursuit of such understanding,mathematicians,biologists and physicists usually used random graphs to model all these real-life networks.For a general introduction,we can see[2–7].

In the model of[2],when m=1,the resulting graph is a tree.These scale-free trees have known since the 1980s as nonuniform random recursive tree.Two nearly identical classes of these trees are random recursive trees with attraction of vertices proportional to the degrees and random plane-orient recursive tree(see[8–13]).Later,the model was generalized by Bollobˊas et al.[14]and Mahmoud[15],in which the probability of choosing an old vertex is (k+β)/Sn,instead of k/2n,with a given β＞-1,where k is the degree of the vertex andSn=(2+β)n+β is the sum of all weights of vertices.

In this paper,we propose a kind of evolving random networks which shows tree structure. We start with two vertices connecting by a single edge,and at every time step,we add a vertex and connect it with one of the existing vertices according to the following rule:

I.with probability 1-α we chose an existing vertex with equal probability;

II.with probability α,we choose an existing vertex with the probability proportional to the degree,that is k/Sn,where k is the degree of the vertex chosen and Sn=2n is the total degree of vertices.

The model shows many dif f erent properties from the existing model,and we show those in following sections.

2 Normal Distribution of Sacled Number of Leaves

In this section and herein after,Dk(n)denotes the number of vertices with degree k at time n,and

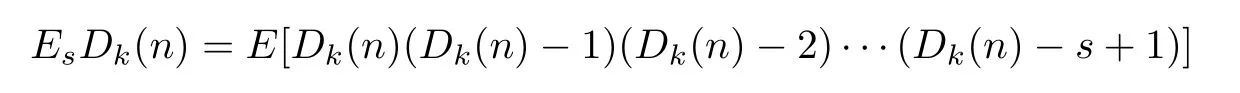
denotes the s-th factorial moment of Dk(n).When k=1,we know that it is the number of leaves in the tree structure,and we have the following lemma:

Lemma 2.1For k=1,we have

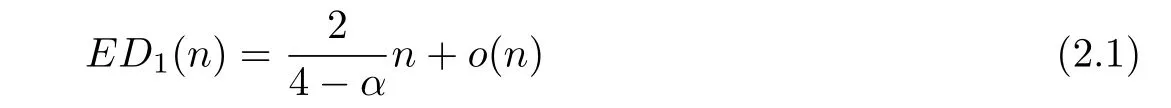
and

where n denotes the evolving time.

Proof.Noticing the evolution of the random network,we can see that for n＞1,the number of vertices of degree 1 either remains unchange if we attach vn+1to a vertex with degree 1 or increases by 1 if we attach vn+1to vertices of degree larger than 1.Hence,

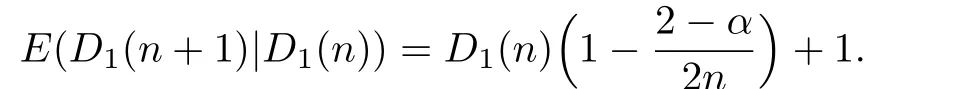
Taking expectation of both sides,we can write

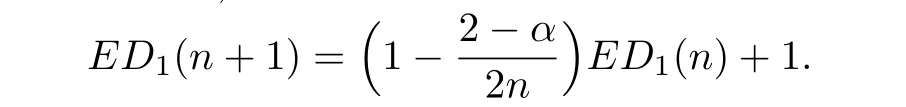
The solution of this recurrence problem with the boundary condition ED1(0)=0 is given by

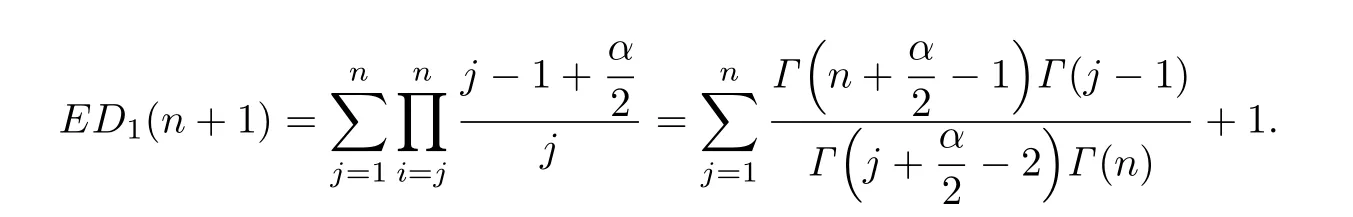
By the Stirling's formula,we obtain

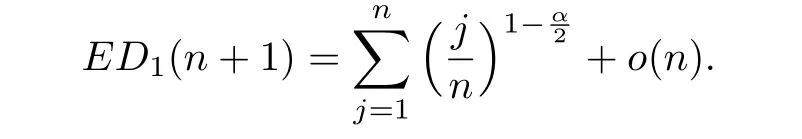
Hence

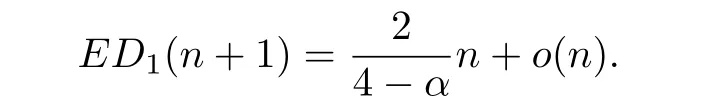
Considering the second factorial moment of D1(n),we have a similar formula

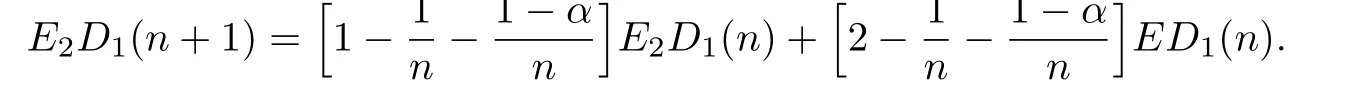
Noticing(2.1)and the fact that E2D1(0)=0,we have

By the Stirling's formula,we obtain

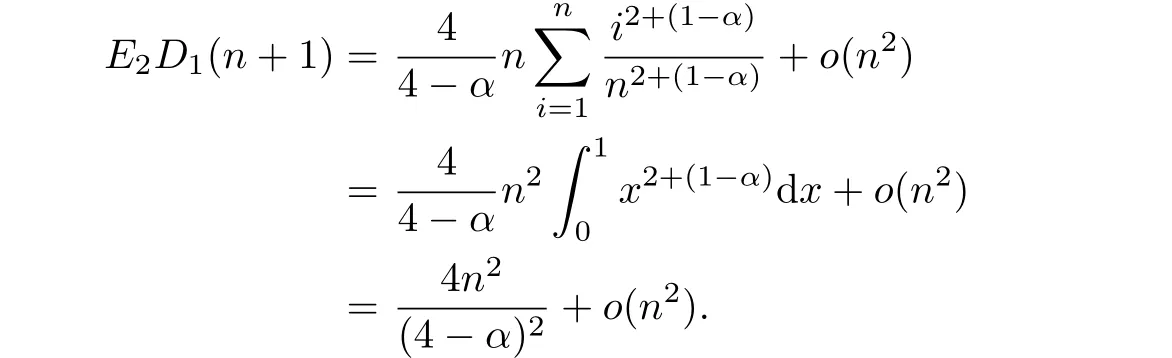
The proof is completed.

By further computation,we have the following lemma:

Lemma 2.2For arbitrary l＞1 and sufficiently large n,one has

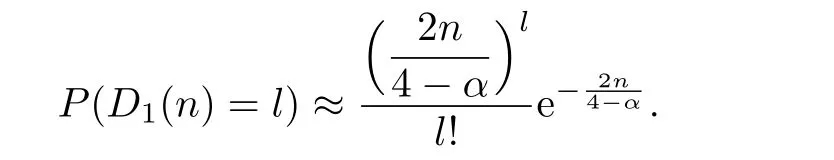
Proof.To prove the distribution obey Poisson distribution with parameterwe need to prove that for any k∈N,the k-th factorial moment of random variable is aboutWe prove the result by mathematical induction.Let

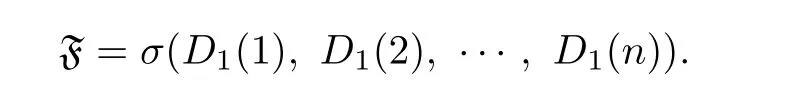
The cases k=1,2 are proved in Lemma 2.1.We assume that the result is true for k,that is,

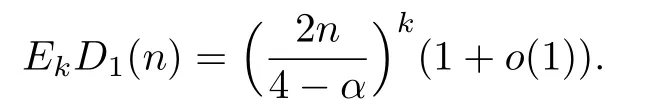
For k+1,we have

Taking expectation of both sides,we can write

Continuing the iteration and noticing the boundary condition

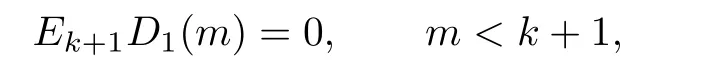
we can write

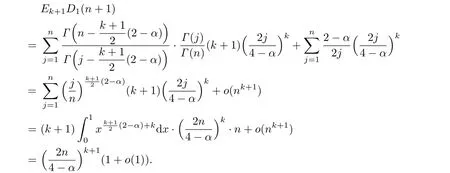
The second equality is obtained by the Stirling's formula.Hence for k+1 the result is also true.The proof is completed.

Theorem 2.1LetThen when n→∞,

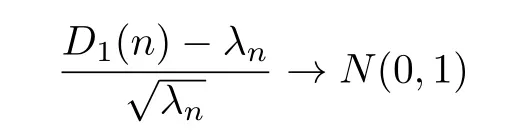
in distribution,where N(0,1)denotes standard normal distribution.

Proof.Clearly,for every k∈N,one has

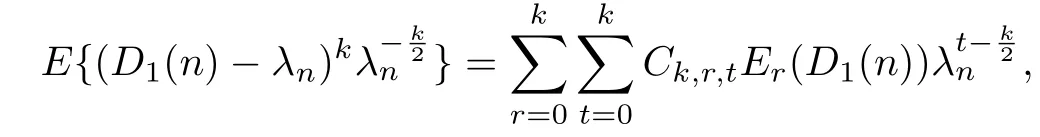
Let Y1,Y2,···be a Poisson random sequence in which Ynhas mean λn.And set

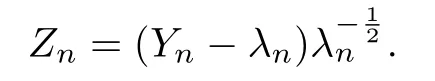
Then Zn→N(0,1)in distribution and so

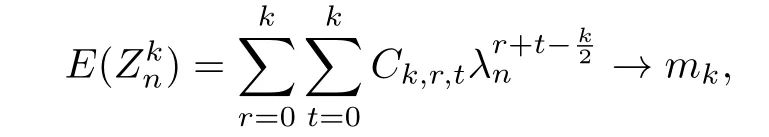
where mkis the k-th moment of N(0,1).Therefore,the k-th moment of the sequencealso converges to mk,and the theorem is proved.

3 Asymptotic Degree Distribution of the Network

In this section,we prove that the degree distribution of our graph is stable almost surely as n→∞around a power law with exponentLetdenote the proportion of vertices with degree i at time n.We have the following lemma.

Lemma 3.1For arbitrary i＞2,the limit

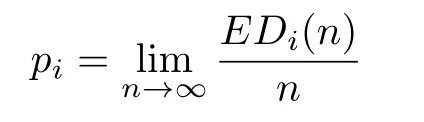
exists and

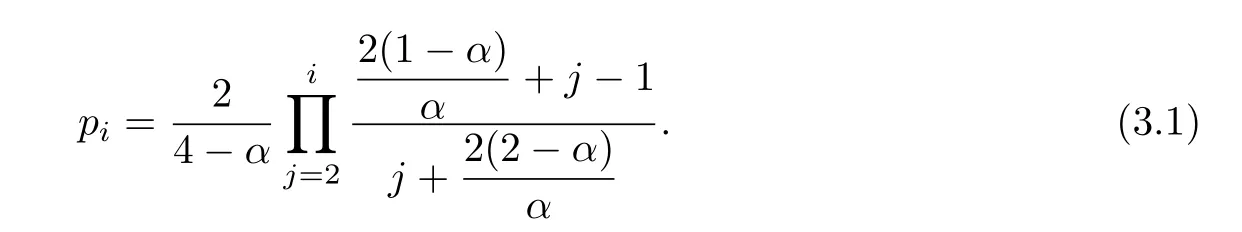
Proof.We prove the lemma by mathematical induction.Considering the expectation of,we have the following relation:

Taking expectation of both sides,we can write

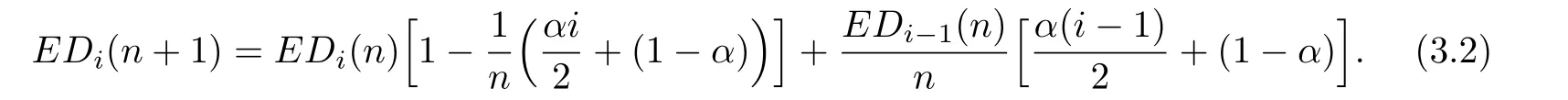
By similar calculation to Lemma 2.1,we have

Assume that the lemma holds for i=k,i.e.,the limit

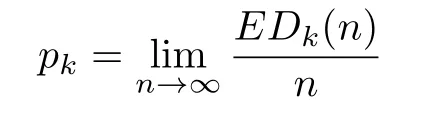
exists and

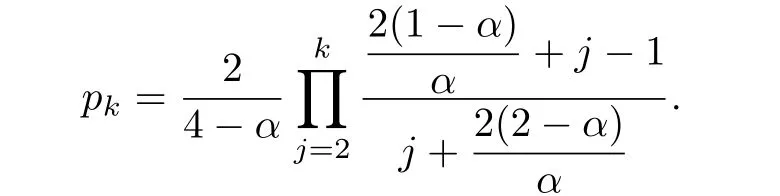
For i=k+1,let

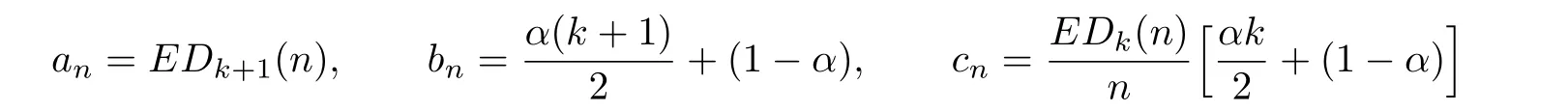
in Lemma 3.1of[3],and using the induction hypothesis for i=k,we know that

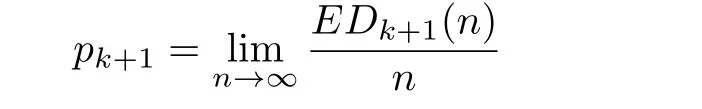
exists and

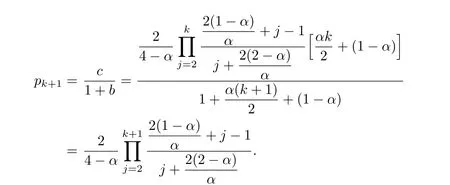
Then the lemma holds for i=k+1,the lemma is proved.

Relation(3.1)can be rewritten as

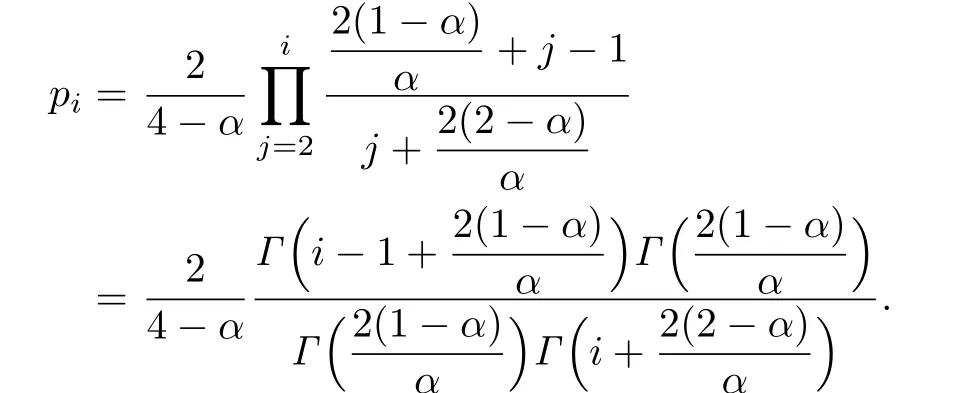
By the Stirling's formula,we obtain

Lemma 3.2For f i xed a＞0 and k,we have

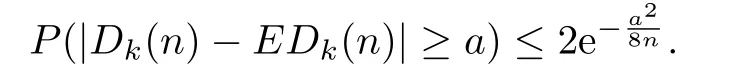
Proof.Let Y1,Y2,···,Yndenote the edge sequence added in the f i rst n time step,and=σ(Y1,···,Yn)denote the σ-algbra.For m=0,1,···,n,let

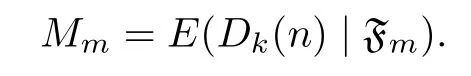
By the tower property of conditional expectation and the fact that the σ-algbracan be deduced from,we obtain that for m＜n,

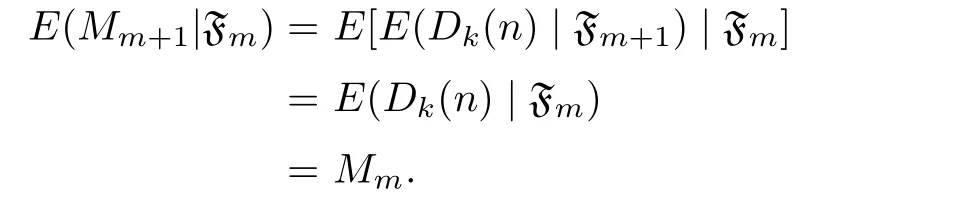
Noticing that

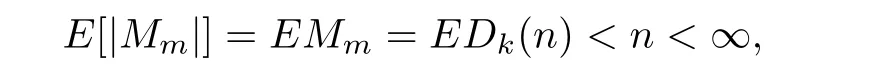
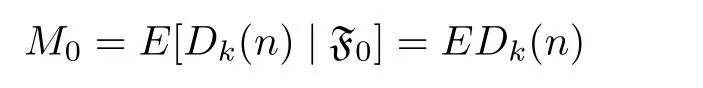
and

Therefore,we have

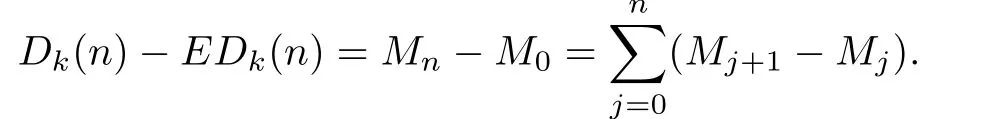
Now we prove

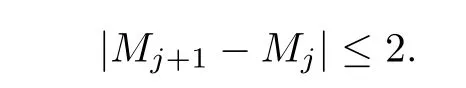
We only prove it for the case k=1,and the others can be proved by the same method. According to the evolution of the network,we can write

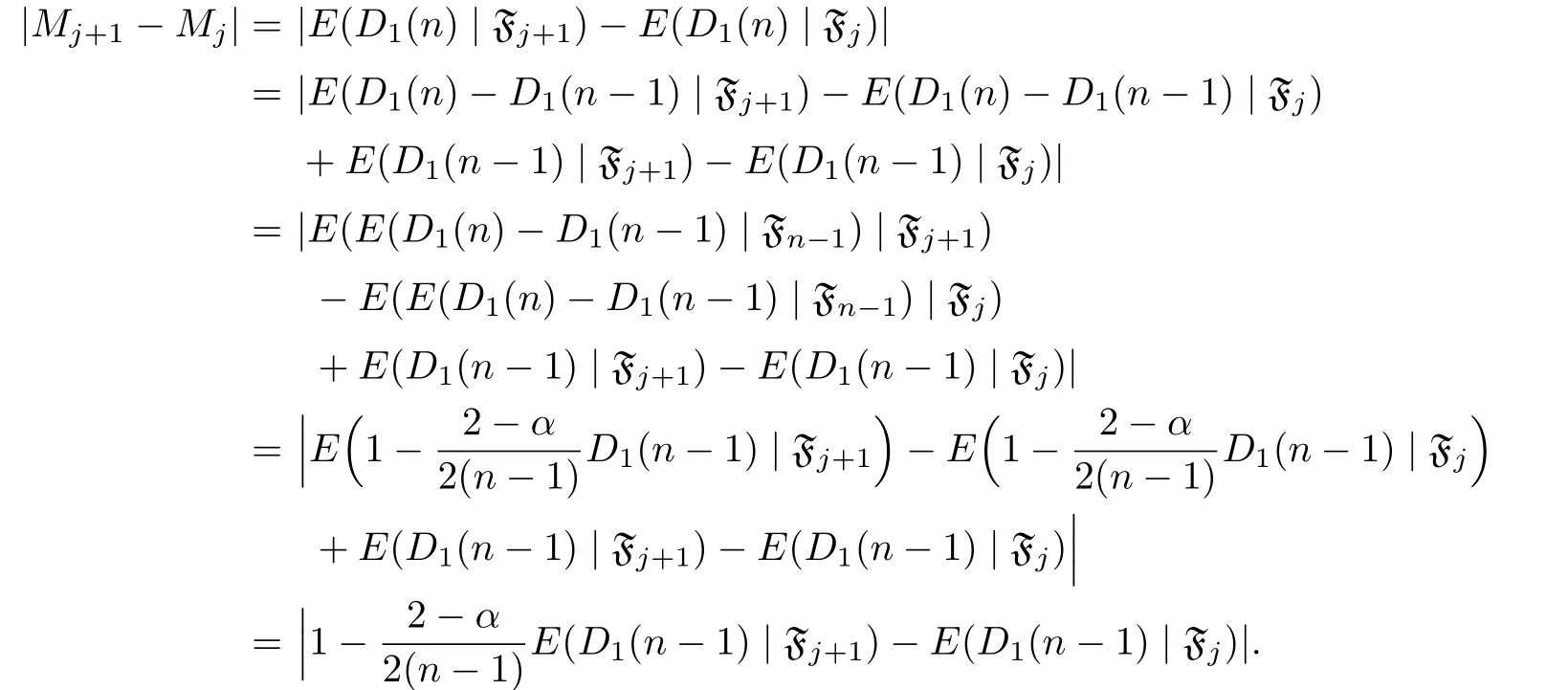
Continuing the iteration and noticing the fact

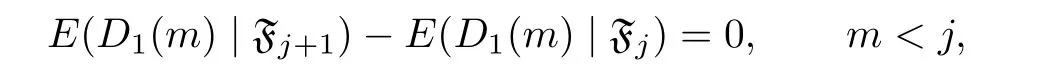
we see that

Obviously,

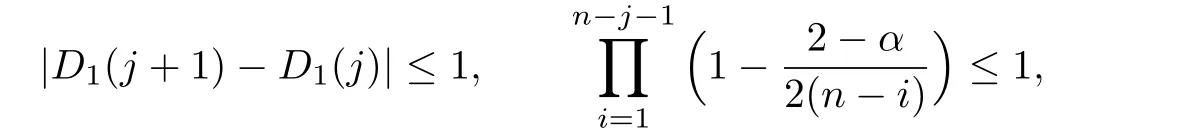
so

By Asume-Hoef f ding's inequality,we have

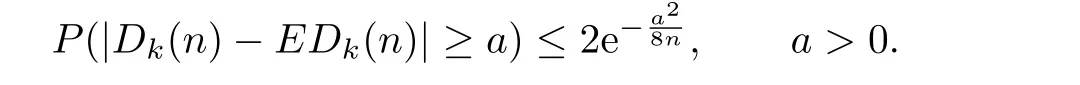
Theorem 3.1In the evolving random network,for f i xed k,we have

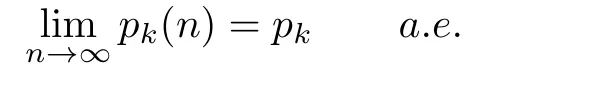
Proof.By the Borel-Cantelli Lemma,we need to prove for arbitrary ε,

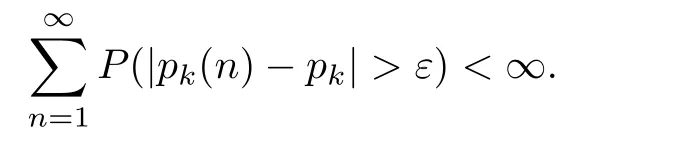
Since

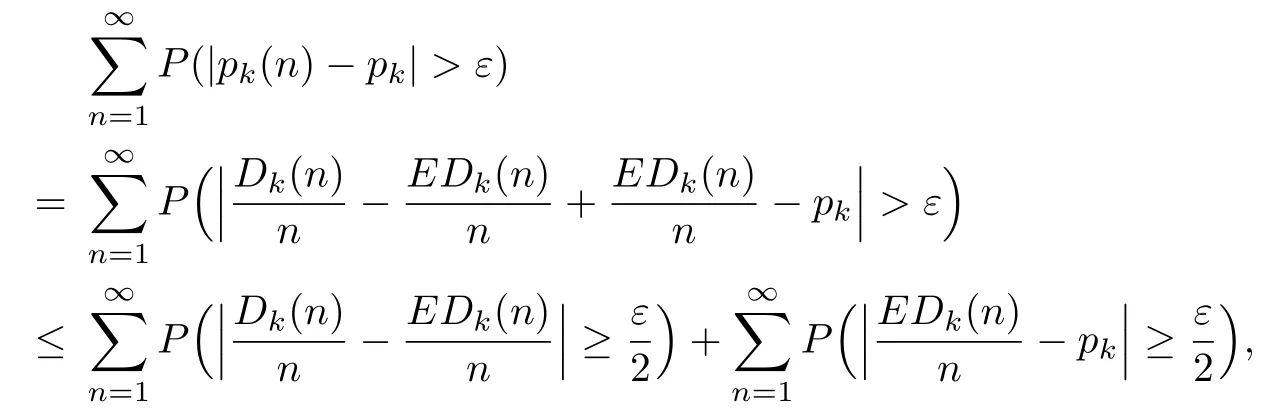
and

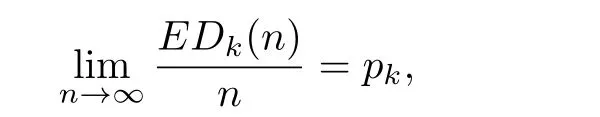
by Lemma 3.2,there exists an N such that

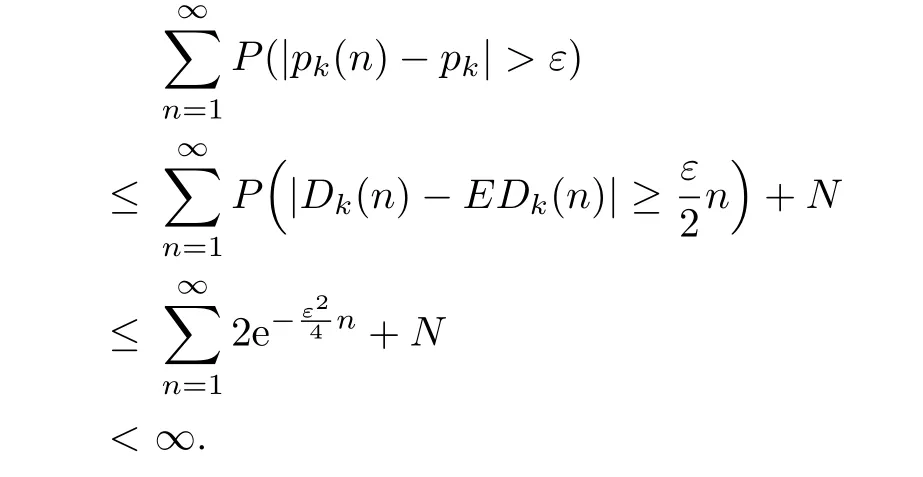
4 Branch Structure of the Network

In this section,we discuss the structure of the network.

Let b(n)denote the number of branch trees of the root,and Y(n,k)denote the number of nodes at distance k from the root at time n.

Theorem 4.1In the evolving random network,for f i xed α,when n→∞,

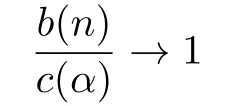
in probability,where

Proof.We just comput the expectation of b(n).According to the structure and formationof the network,we have

Taking expectation of both sides,we obtain

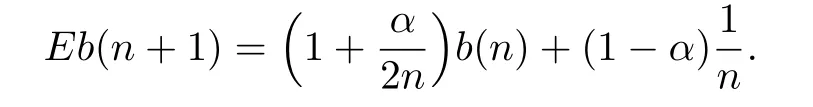
Continuing the iteration and noticing the fact

we obtain

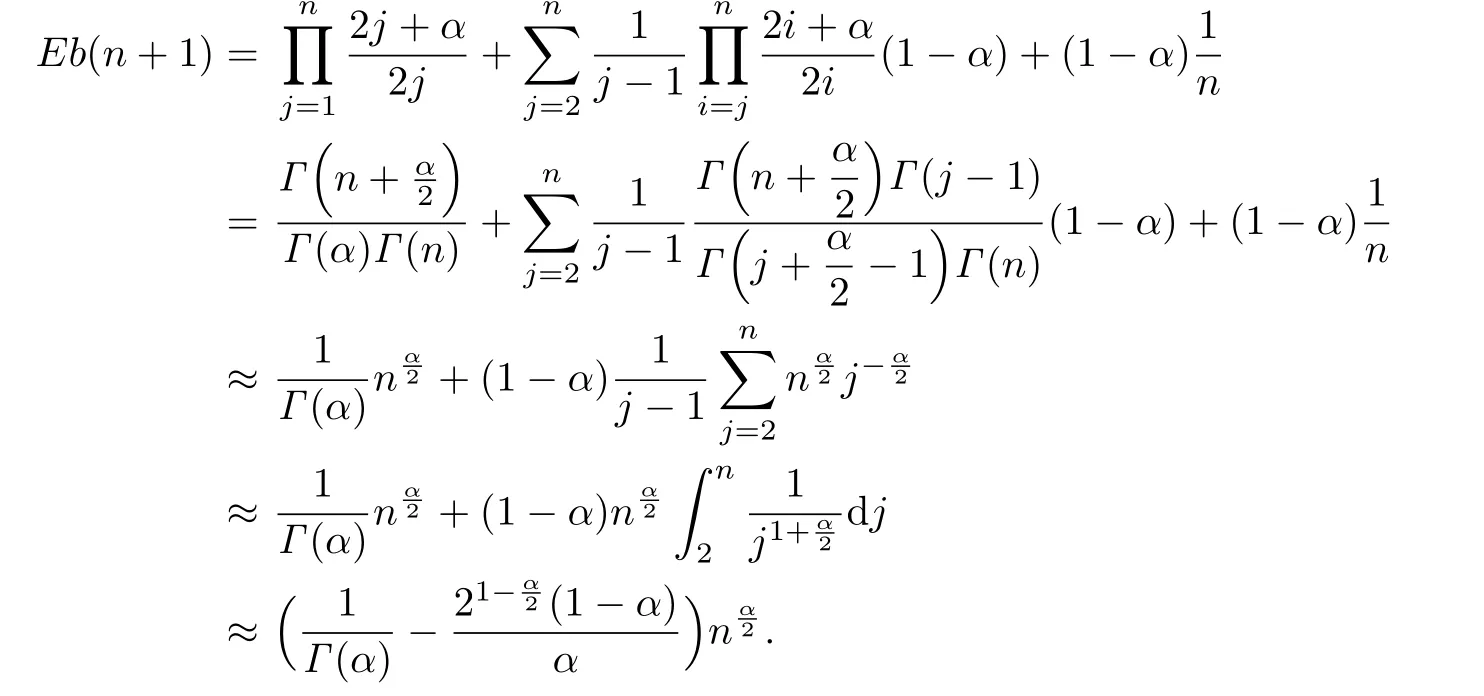
Note that the previous second equation is obtained by the Stirling's formula.The proof is completed.

Theorem 4.2In the evolving random network,for f i xed k and n,

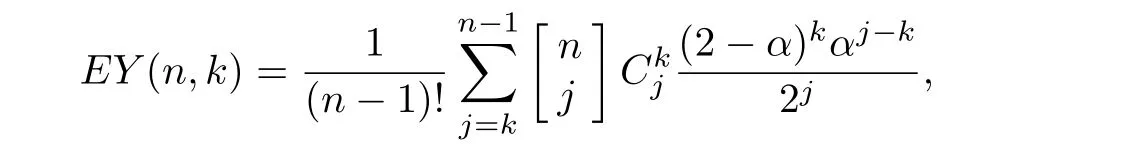
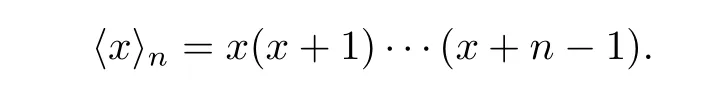
Proof.By the formation of network,we have

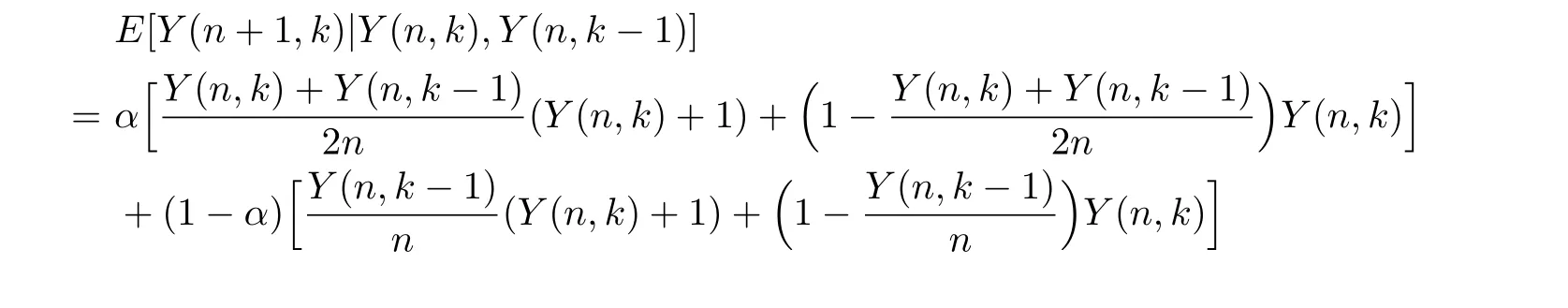
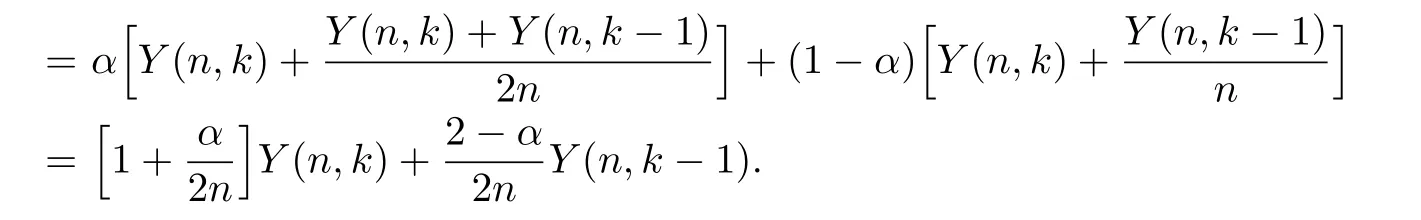
Taking expectation of both sides,we have

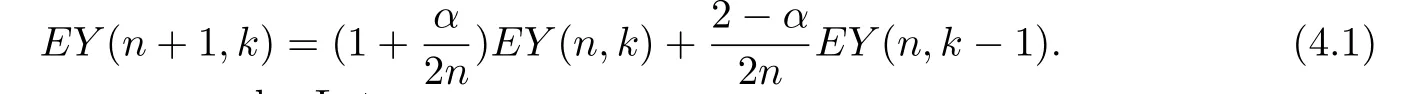
Now,we introduce a monopoly.Let

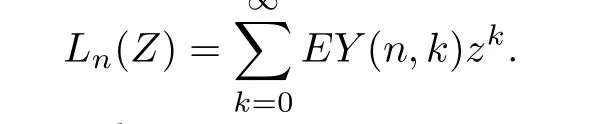
Multiplying both sides of(4.1)byand summing up from 0 to∞,we have

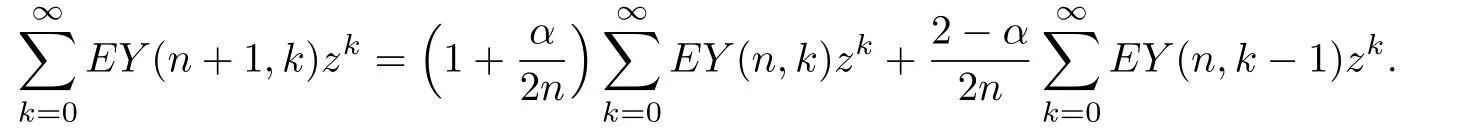
Noticing

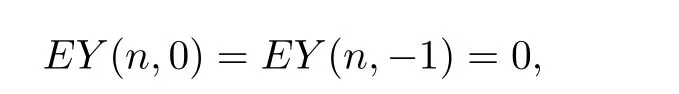
we arrive at

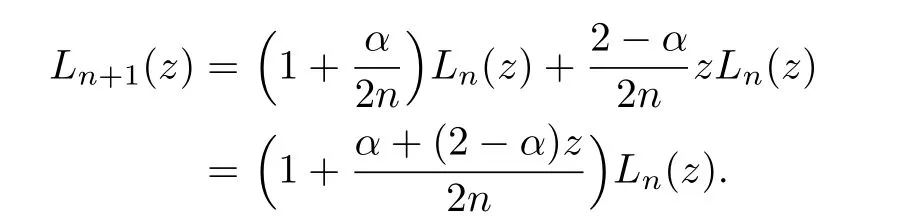
Noting that L1(z)=z,we have

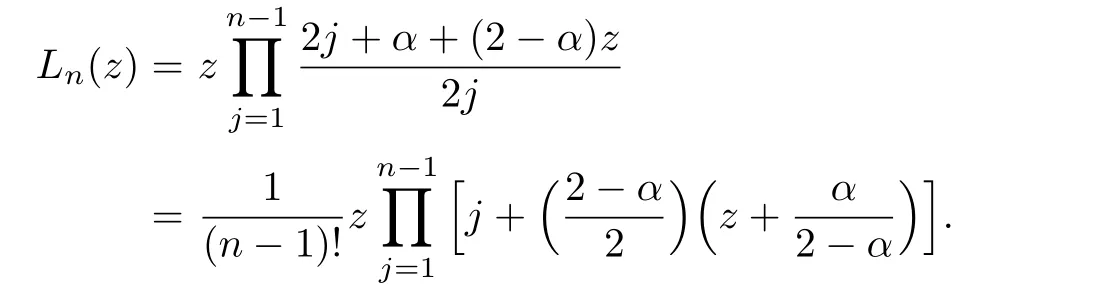
So

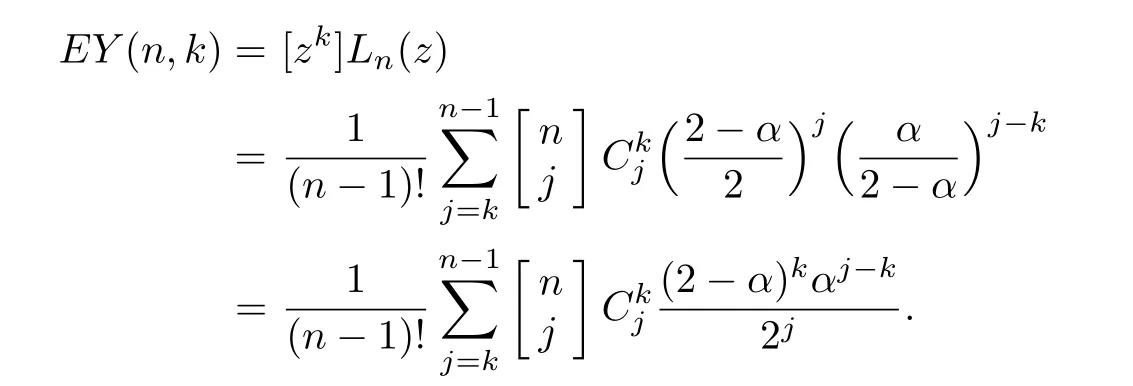
5 Asymptotic Convergence of Maximum Degree

In this section,we discuss the layered structure and maximun degree of the network.

Let X(n,j)denote the degree of node j at time n,and Δ(n,j)denote the increasing degree at node j from time n to time n+1.Obviously,we have

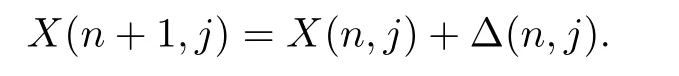
Theorem 5.1In the evolving random network,the expectation of X(n,j)satisf i es

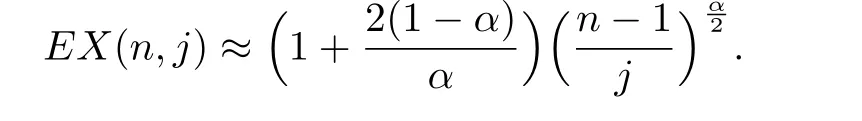
Proof.As the network is formed by adding one node at every time step,we have

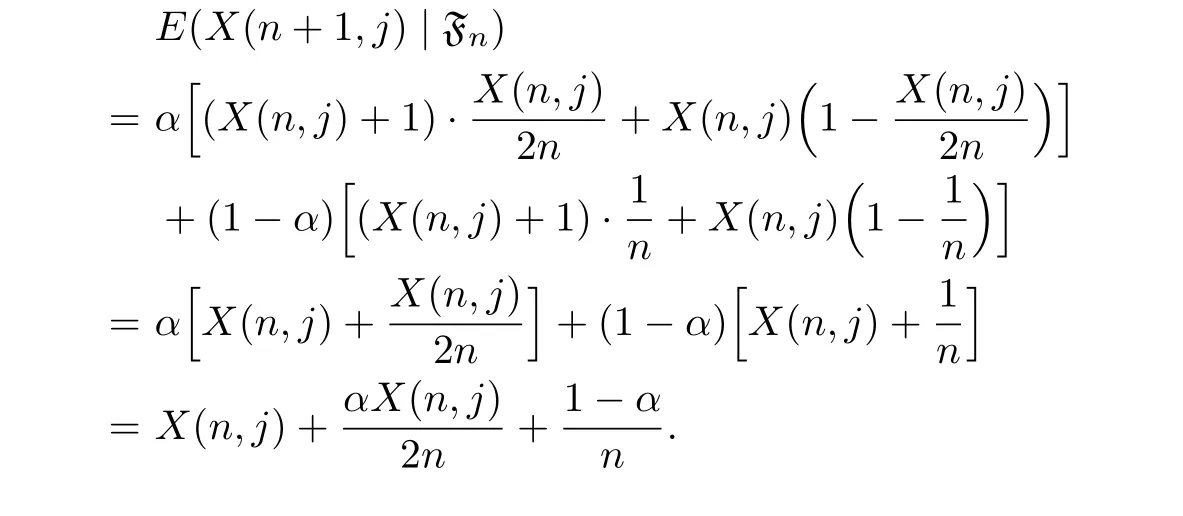
Let

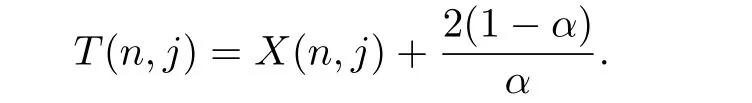
We have

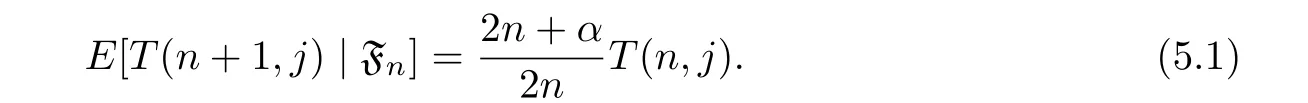
Taking expectation of both sides,we get

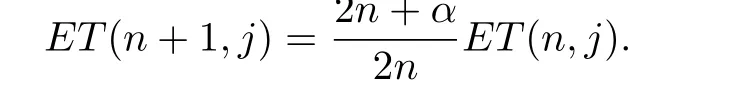
Solving the above equation with boundary condition

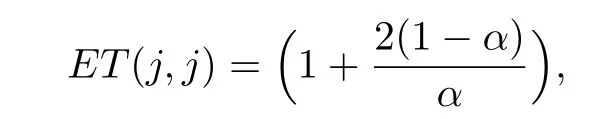
we obtain

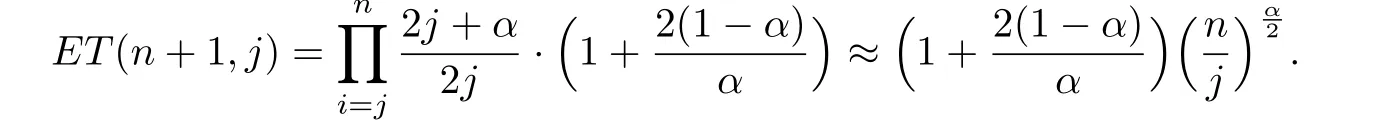
Thus the theorem is proved.

Let

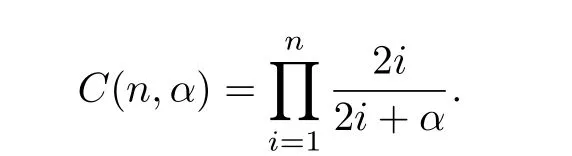
Denote

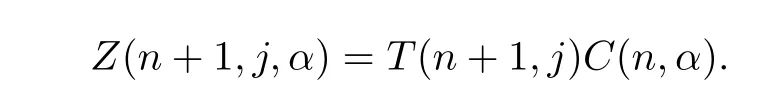
We have the following theorem:

Theorem 5.2(Z(n,j,α))is a positive martingale.

Proof.For the random variable Z(n+1,j,α),taking the conditional expectation of Fn,we have

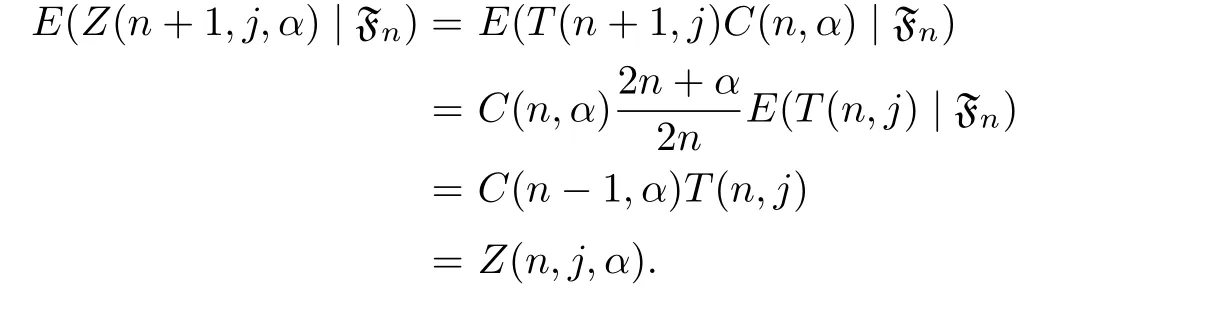
Obviously,the random variable Z(n,j,α)is positive,so it is a positive martingale.The theorem is proved.

Let (

)

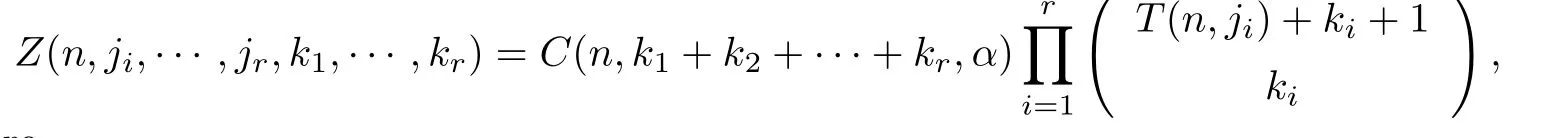
where

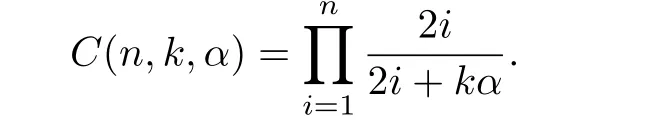
We have the following proposition:

Proposition 5.1For positive numbers j1,···,jr,k1,···,kr,(Z(n,j1,···,jr;k1,···, kr),)is a positive martingale. Proof.Noticing the fact

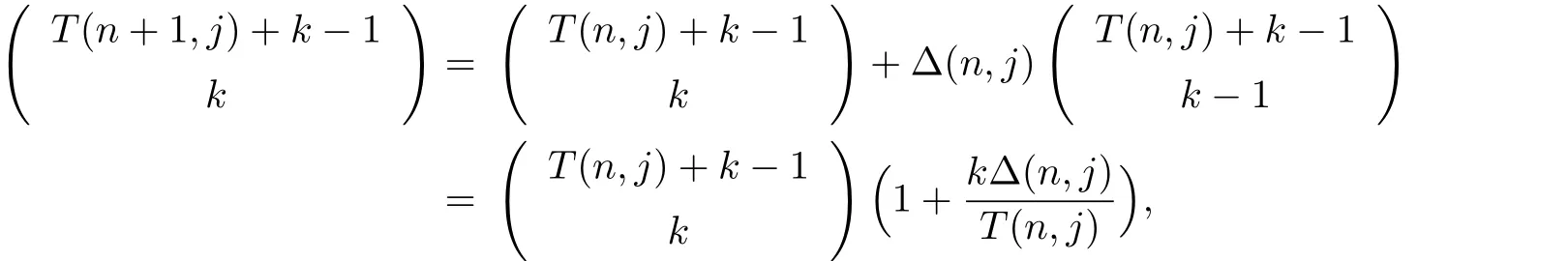
we can obtain (

We can reach the equation because at most one of the Δ(n,ji)(i=1,···,r)is not 0.

Taking conditional expectation about random variable Z(n,j1,···,jr;k1,···,kr),we obtain

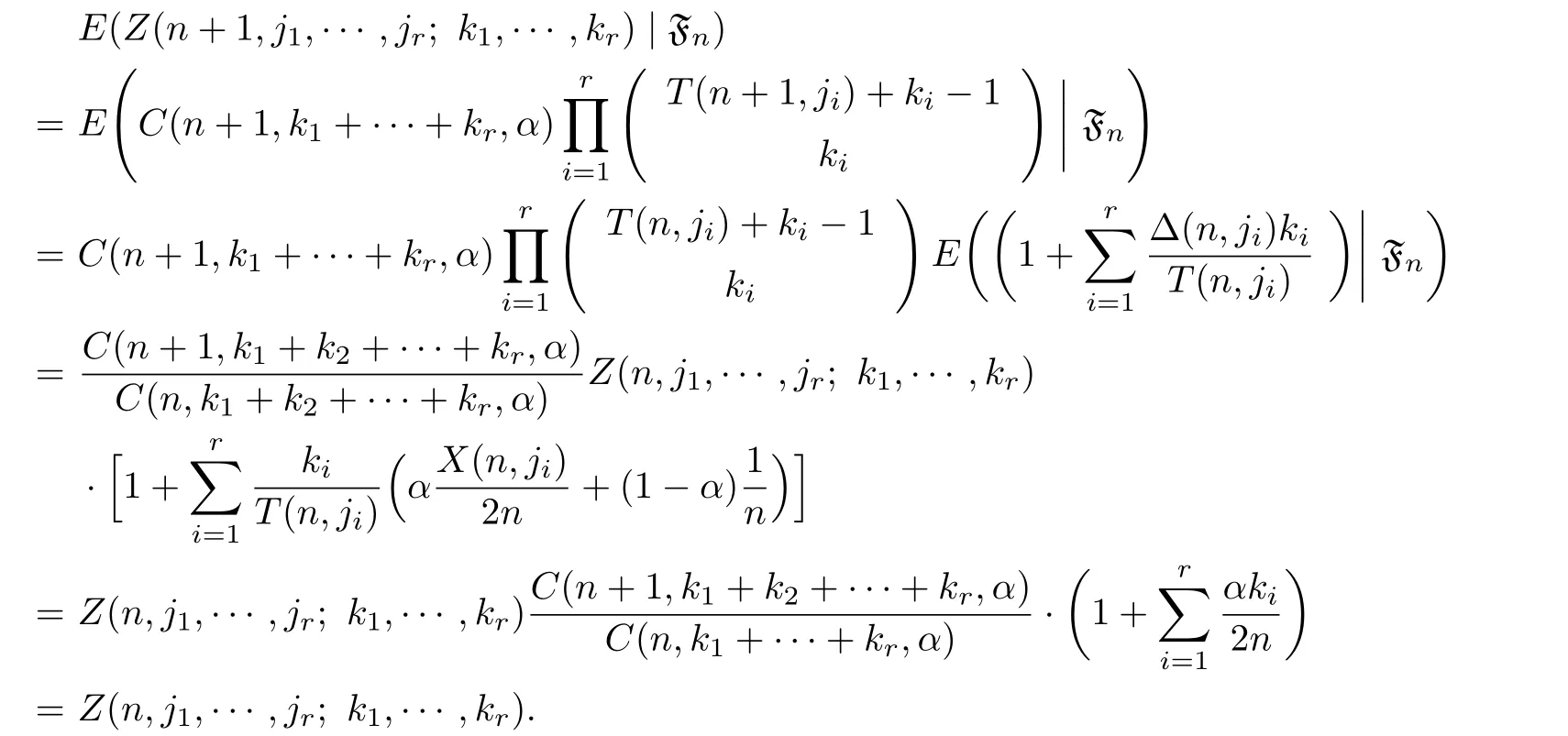
Thus,Z(n,j1,···,jr;k1,···,kr)is a positive martingale.The proof is completed.

By the convergence theorem of martingale,we can assume that

For arbitrary i and j(i＜j),considering the relation of varible ζiand ζj,we obtain the following theorem.

Theorem 5.3For the random variables ζiand ζj(i＜j),we have

(1)The two random variables are positive correlated when

(2)The two random variables are negative correlated when

Proof.By the property of martingale,we have

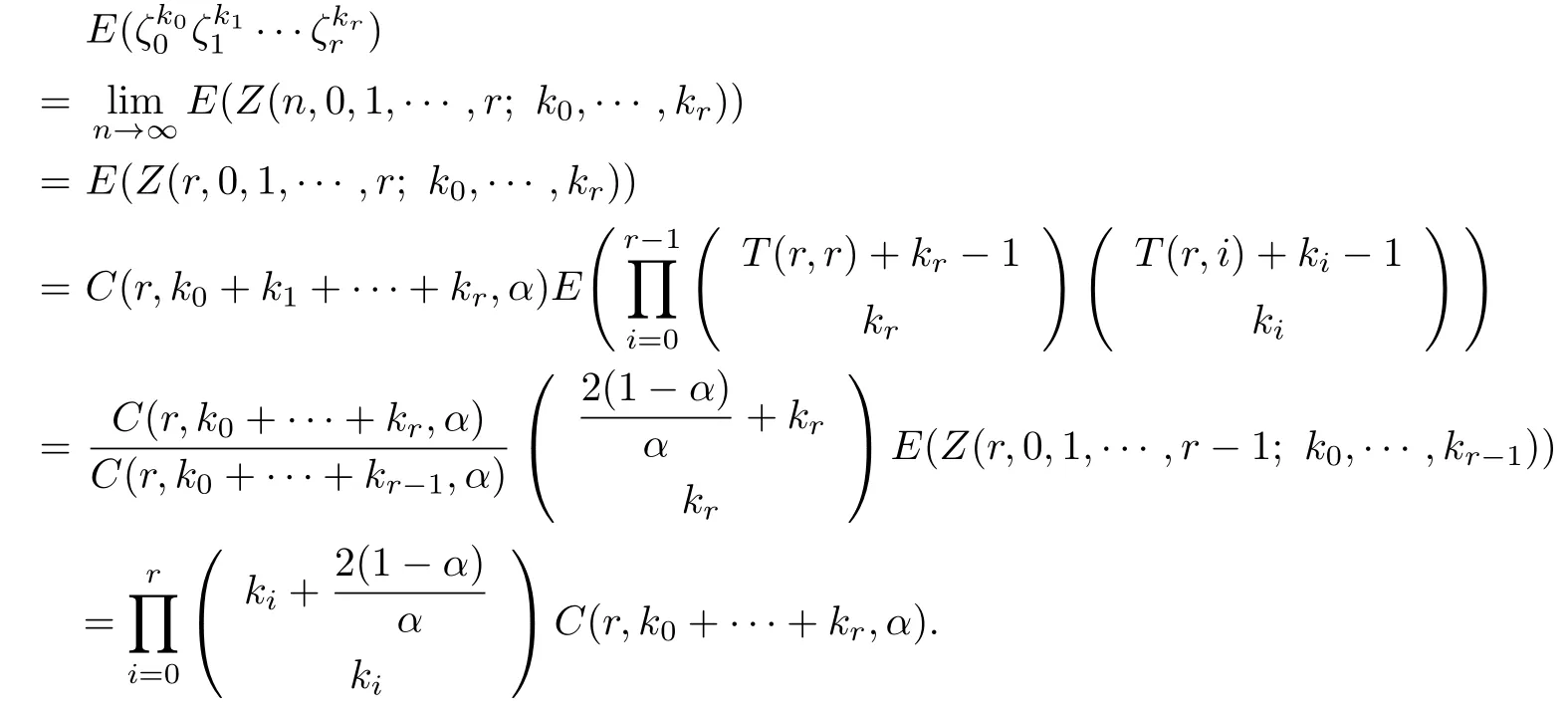
For arbitrary i＜j,let k0=k1=···=ki1=ki+1=···=kj-1=0 and r=j.Then we have

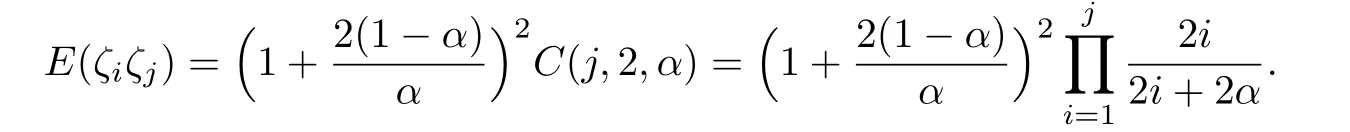
Hence

The proof is completed.

As a special case in the previous proof,one can reach

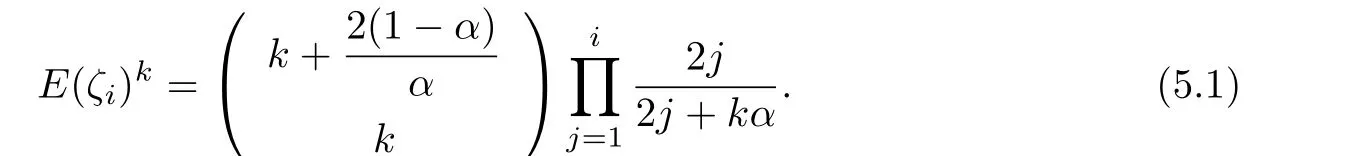
Now,we consider the maximum degree.Let Mndenote the maximum degree of the network at step n,

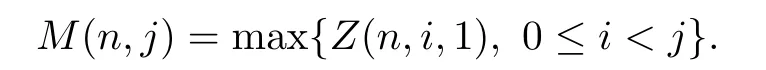
Obviously,

We have the following theorem:

Theorem 5.4There existaand a variableµsuch that

Proof.Notice that{M(n,n),Fn}is a submartingale sequences because{Z(n,j,1),Fn}is a martingale.We prove that the submartingale is bounded in Lk.In fact,

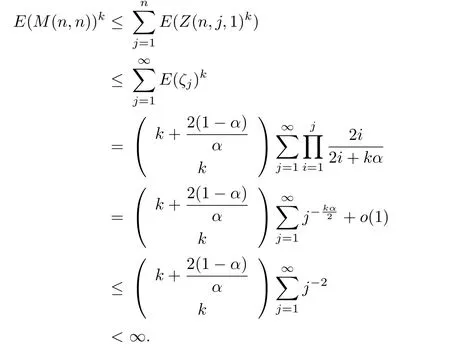
The next step is to prove thatis a Cauchy sequence in Lk.For arbitrary i,j with i＜j＜n,we have

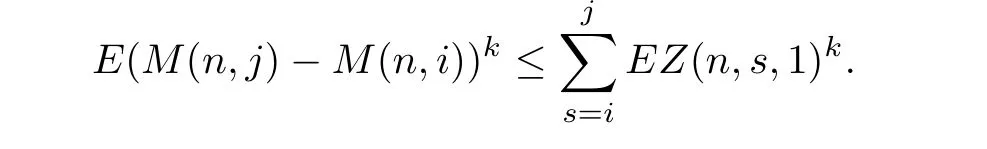
Let n→∞,we get

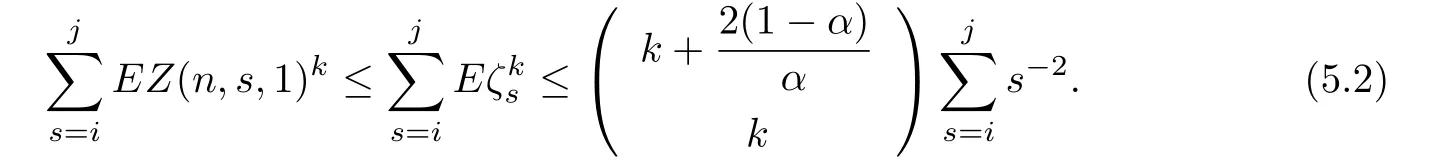
The last term of(5.2)can be arbitrary small when i,j grow sufficiently large.So thereexists a variable such that

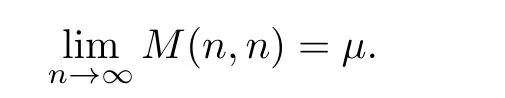
As

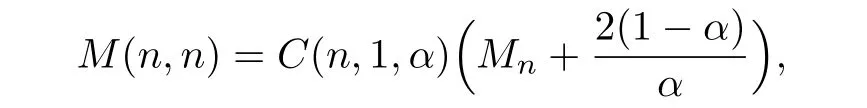
the theorem is proved.

[1]Watts D J.Small Worlds:the Dynamics of Networks between Order and Randomness.Princeton:Princeton Univ.Press,2003.

[2]Barabˊasi B,Albert R.Emergence of scaling in random networks.Science,1999,286:509–512.

[3]Aliello W,Chung F,Lu L Y.Random Evolution in Massive Graphs.in:James A,Panos M P,Mauricio G,Resende C.Handbook on Massive Data Sets.New York:Kluwer Academic Publishers,1998.

[4]Barabˊasi A L.Linked:How Everything Is Connected to Everything Else and What It Means. New York:PLUME.Penguin Group Inc.,2003.

[5]Bollobˊas B,Riordan O.Mathematical Results on Scale-free Random Graphs.in:Terveen K, Admic L.Handbook of Graphs and Networks.Berlin:Willey-VCH Publishers,2002:436–454.

[6]Dorogovtsev S N,Mendes J F.Evolution of networks.Adv.in Phys.,2002,51:1079–1094.

[7]Newman M E J.The structure and function of complex networks.SIAM Review,2003,45: 167–208.

[8]Mahmoud,Smyth H R,Szymanski J.On the structure of plane-orient recursive trees and their branchs.Random Structures Algorithms,1993,4:151–176.

[9]Mori T F.On random trees.Studia Sci.Math.Hungar,2002,39:143–155.

[10]Lu J L,Feng Q.Strong consistency of the number of vertices of given degrees in nununiform random recursive tree.Yokohama Math,1998,45:61–69.

[11]Szymanski J.On the nununiform random recursive tree.Ann.Discrete Math,1987,33:297–306.

[12]Biggins J D,Grey D R.A note on the growth of random trees.Statist.Probab.Let.,1997,32: 339–342.

[13]Katona Z,Mori T F.A new class of scale free and random graphs.Statit.Probab.Let.,2006, 76:1587–1593.

[14]Bollobˊas B,Riodan O,Spencer J,Tusnady G.The degree sequence of a scale-free random graph process.Random Structure Algorithms,2001,18:270–290.

[15]Mahmoud,Smyth H R.A survy of recursive tree.Theory Probab.Math.Statist.,2001,51: 1–29.

A

1674-5647(2013)03-0203-15

Received date:July 12,2010.

The NSF(71271003)of China,the Programming Fund(12YJC630111,12YJA790041)of the Humanities and Social Sciences Research of the Ministry of Education of China,the NSF(10040606Q03)of Anhui Province,and Key University Science Research Project(KJ2013A044)of Anhui Province.

E-mail address:zmli08@ahpu.edu.cn(Li Z M).

2000 MR subject classif i cation:05C07,05C75