A Class of*-simple Type A ω2-semigroups(I)
SHANG YUAND WANG LI-MIN
(1.Department of Mathematics,Simao Teacher's College,Puer,Yunnan,665000) (2.School of Mathematics,South China Normal University,Guangzhou,510631)
Communicated by Du Xian-kun
A Class of*-simple Type A ω2-semigroups(I)
SHANG YU1AND WANG LI-MIN2
(1.Department of Mathematics,Simao Teacher's College,Puer,Yunnan,665000) (2.School of Mathematics,South China Normal University,Guangzhou,510631)
Communicated by Du Xian-kun
In this paper,we study*-simple type A ω2-semigroups in which D*=~D and D*|ES=Mdby the generalized Bruck-Reilly extension and obtain its structure theorem.We also obtain a criterion for isomorphisms of two such semigroups.
type A semigroup,*-simple ω2-semigroup,generalized Bruck-Reilly extension
1 Introduction and Preliminaries
Earlier investigations in[1]studied*-bisimple type A ω2-semigroups whose equivalence D*and~D coincide,characterizing them as the generalized Bruck-Reilly*-extensions of cancellative monoids.The results of[1]generalize those of regular bisimple ω2-semigroups. In this paper,as a natural follow up on these investigations,we study*-simple type A ω2-semigroups in which D*=~D and D*|ES=Md.
The theory developed here closely parallels the one for regular simple ω2-semigroups. In Sections 2 and 3,it is shown that the*-simple type A ω2-semigroups in which D*=~D and D*|ES=Mdare precisely the generalized Bruck-Reilly extensions of an ω-chain of cancellative monoids of length d.In Section 4,we obtain an isomorphism theorem for such semigroups.
We complete this section with a summary of notions of type A semigroups,the details of which can be found in[1–3].
For any semigroup S we denote by ESthe set of idempotents of S.We def i ne a partial ordering≥on ESby the rule that e≥f if and only if ef=f=fe.Let a,b∈S such that for all x,y∈S1,ax=ay if and only if bx=by.Then a,b are said to be L*-equivalent andwritten aL*b.Dually,aR*b if for all x,y∈S1,xa=ya if and only if xb=yb.If S has an idempotent e,the following characterisation is known.
Lemma 1.1[3]Let S be a semigroup,and e be an idempotent in S.Then the following are equivalent:
(i)eL*a;
(ii)ae=a and for all x,y∈S1,ax=ay implies ex=ey.
By duality,a similar condition holds for R*.A semigroup in which each L*-class and each R*-class contain an idempotent is called an abundant semigroup(see[2]).The join of the equivalence relations L*and R*is denoted by D*and their intersection by H*.Thus aH*b if and only if aL*b and aR*b.In general,L*◦R*/=R*◦L*and neither equals D*.Basically,aD*b if and only if there exist elements x1,x2,···,x2n-1in S such that aL*x1R*x2L*···L*x2n-1R*b.Let H*be an H*-class in a semigroup S with e∈H*,where e is an idempotent in S.Then H*is a cancellative monoid.Denote by R,L the left and right Green's relations respectively,on S.It is well-known that L⊆L*,R⊆R*,D⊆D*, H⊆H*for a semigroup S and if a,b are regular elements of S,then aL*b(aR*b)if and only if aLb(aRb).
To avoid ambiguity we at times denote a relation K on S by K(S).The following notation will be used.An L*-class containing an element a∈S is denoted by L*a.Similarly,R*ais an R*-class with an element a∈S.Let S be a semigroup and I an ideal of S.Then I is called a*-ideal if L*a⊆I and R*a⊆I for all a∈I.The smallest*-ideal containing a is the principal*-ideal generated by a and is denoted by J*(a).For a,b in S,aJ*b if and only if J*(a)=J*(b).The relation J*contains D*.A semigroup S is said to be*-simple if the only*-ideal of S is itself.Clearly,a semigroup is*-simple if all its elements are J*-related. Let S be a semigroup with a semilattice E of idempotents.Then S is called a right adequate semigroup if each L*-class of S contains a unique idempotent.Dually,we have the notion of a left adequate semigroup.A semigroup which is both left and right adequate is called an adequate semigroup.In an adequate semigroup each L*-class and each R*-class contain unique idempotent.For an element x of an adequate semigroup S,x*(x+)denotes the unique idempotent in the L*-class L*x(R*-class R*x)of x.A right(left)adequate semigroup S is called a right(left)type A semigroup if ea=a(ea)*(ae=(ae)+a)for all elements a in S and all idempotents e in S.An adequate semigroups S is type A if it is both right and left type A.
Lemma 1.2[4]Let S be an arbitrary semigroup.Then the following are equivalent:
(i)For all idempotents e and f of S the element ef is regular;
(ii)〈ES〉is a regular subsemigroup;
(iii)Reg(S)is a regular subsemigroup.
(i)φα,αis the identity map for each α∈Y;
(ii)φα,βφβ,γ=φα,γfor every α,β,γ∈Y such that α≥β≥γ, and such that the product in S is given by
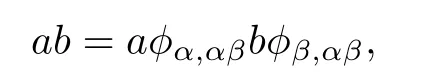
where a∈Sα,b∈Sβ.We write
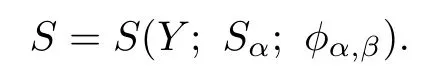
Let S be an adequate semigroup with semilattice of idempotents E and let
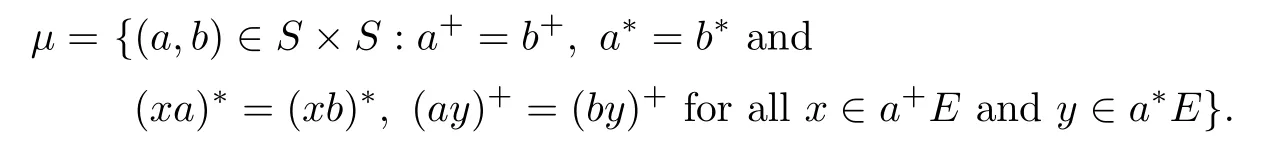
Thenµis the largest congruence contained in H*.
Lemma 1.3[3]Let S be an adequate semigroup with semilattice of idempotents E.Then the following conditions are equivalent:
(i)S/µ~=E;
(ii)for all elements a of S,a*=a+;
(iii)L*=H*=R*;
(iv)each H*-class of S contains an idempotent;
(v)E is central in S;
(vi)S is a strong semilattice of cancellative monoids.
Furthermore,if the above conditions hold,then D*∩(E×E)=1E.
Let N0be the set of all nonnegative integers and N be the set of all positive integers. The set N0×N0with the order def i ned by
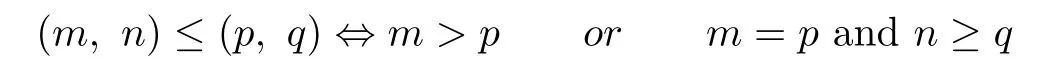
is called an ω2-chain,and denoted by Cω2.Any partially ordered set order isomorphic to Cω2is also called an ω2-chain.We say that a semigroup S is an ω2-semigroup if and only if ESis order isomorphic to Cω2.Thus,if S is an ω2-semigroup,then we can write
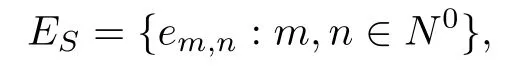
where em,n≤ep,qif and only if(m,n)≤(p,q).In[1],Shang and Wang have shown that the set S=N0×N0×N0×N0with the operation def i ned by
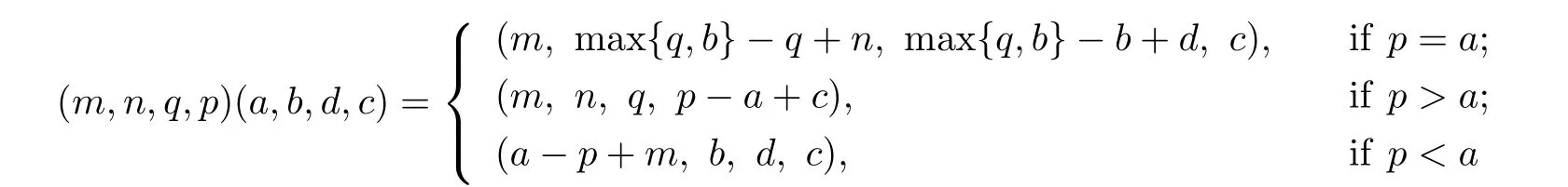
is a bisimple ω2-semigroup,which is called the quadrucyclic semigroup,and is denoted by Bω2.
Consider a monoid M with H*eas the H*-class which contains the identity element e of M.The set S=N0×M×N0with an opertation def i ned by
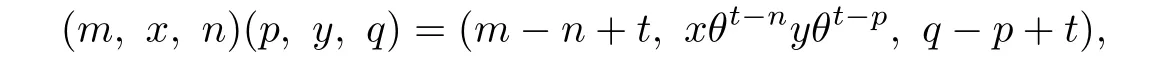
where t=max{n,p}and θ is an endomorphism of M with images inis a semigroup with an identity(0,e,0).The semigroup S=N0×M×N0constructed above is called thegeneralized Bruck-Reilly extension of M determined by θ,and is denoted by S=BR*(M,θ). Let(m,x,n)∈S.Then(m,x,n)is an idempotent if and only if m=n and x is an idempotent.Furthermore,(m,a,n)is a regular element of S if and only if a is a regular element.An element(m,a,n)in S has an inverse(p,b,q)∈S if and only if b is the inverse of a in T,and p=n,q=m.For any(m,a,n),(p,b,q)∈BR*(M,θ),it can be verif i ed that
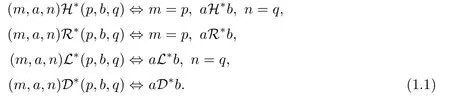
Let S be a type A semigroup with a semilattice of idempotents E.Then S is called a type A ω2-semigroup if E is an ω2-chain.Thus in a type A ω2-semigroup ES={em,n:m,n∈N} and em,n≥ep,qif and only if(m,n)≥(p,q).In such a semigroup S,we denote by L*m,n(resp.)the L*-class(resp.R*-class)containing idempotent em,n,that is,
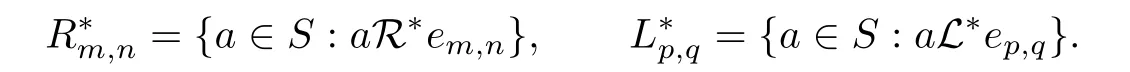
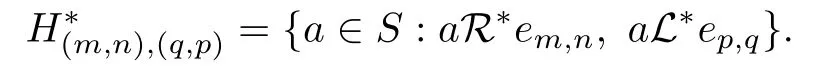
In[1],we obtaind the following lemma.
Lemma 1.4Let S be a type A ω2-semigroup.Then
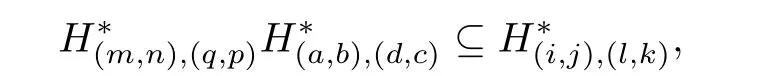
where
Let S be a type A semigroup,a,b∈S.The relationis def i ned on S by
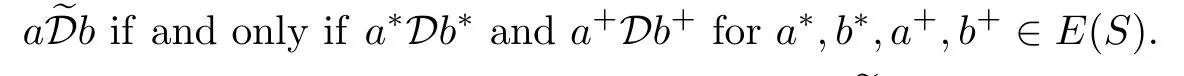
Lemma 1.5[5]Let S be an adequate semigroup.The following conditions are equivalent:
(i)D*=~D;
(ii)every nonempty H*-class contains a regular element. Furthermore,if(i)and(ii)hold,then
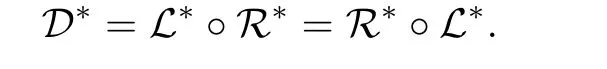
However,as an example in[6]shows,(i)and(ii)are not necessary conditions for the equality
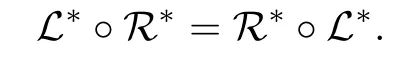
Other basic results discussed in[1]and[2]will be assumed.The notations adopted are similar to those in[2,7].
Let S be a*-simple type A ω2-semigroup with the set{em,n:m,n∈N0}of idempotents, and let d be any positive integer.Let em,n,ep,q∈ES.The relation Mdis def i ned on ESby
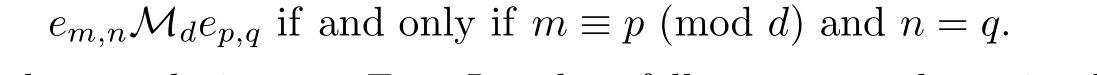
Mdis an equivalence relation on ES.In what follows we study*-simple type A ω2-semigroups in which D*=and D*|ES=Md.
2 The*-simple Type A ω2-semigroup in which D*=and D*|ES=Md:Construction
In this section we give a process for constructing a*-simple type A ω2-semigroup in which D*=and D*|ES=Mdfrom a inf i nite set of cancellative monoids and a homomorphism. In particular,the number of D*-classes of such semigroup is inf i nite.It will then be shown in Section 3 that this construction yields the most general type of*-simple type A ω2-semigroups in which D*=and D*|ES=Md.
We now take T to be a strong semilattice of cancellative monoids.More precisely,let
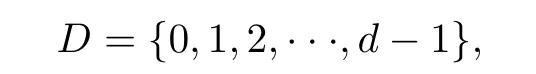
where d is a positive integer;let{Ti,j:(i,j)∈D×N}be set of parewise-disjoint cancellative monoids;for each(i,j)∈D×N0,let α(i,j),(i,j)be the identity map of Ti,j,and for each pair (i,j),(k,l)∈D×N0where(i,j)>(k,l),there is a homomorphism α(i,j),(k,l):Ti,j→Tk,lsuch that for all(i,j),(k,l),(m,n)in D×N0with(i,j)≥(k,l)≥(m,n),
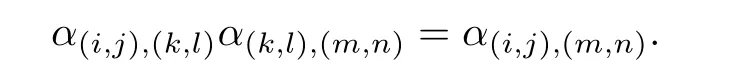
So we have a semigroup
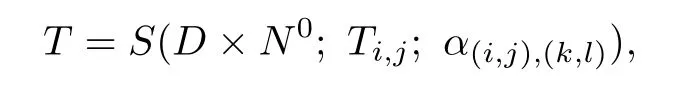
in which the semilattice D×N0is the chain
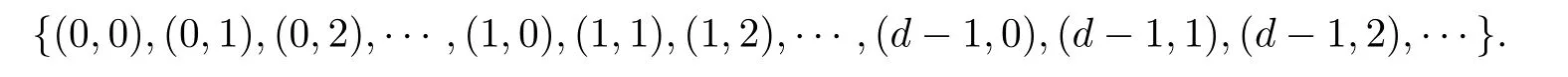
We denote the idempotents of T by f0,0,f0,1,f0,2,···,f1,0,f1,1,f1,2,···,fd-1,0,fd-1,1, fd-1,2,···(the identity elements of T0,0,T0,1,T0,2,···,T1,0,T1,1,T1,2,···,Td-1,0,Td-1,1, T,···,respectively),and note that,in T,
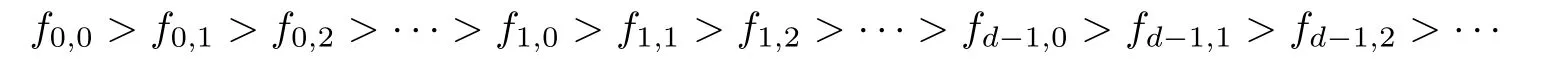
The element f0,0is the identity of T.We refer to T as an ω-chain of cancellative monoids of length d.It is easy to see that T is a type A monoid.
Let θ:T→T0,0be a homomorphism on T.Consider the triples
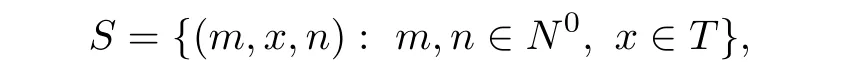
such that for(m,x,n),(p,y,q)in S,their product is given by
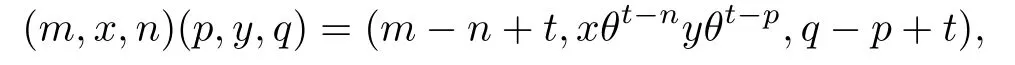
where t=max{n,p}.
Lemma 2.1S is the generalized Bruck-Reilly extension BR*(T,θ)of T determined by θ.
Proof.From[6]S is a semigroup,the generalized Bruck-Reilly extension of T,determined by θ and denoted by BR*(T,θ).From[6],(0,f0,0,0)is the identity element in S and (m,x,n)in S has an inverse if and only if x in T has an inverse.Also,(m,x,n)in S is an idempotent if and only if x=fi,j∈Ti,j,(i,j)∈D×N0and m=n.
Lemma 2.2A generalized Bruck-Reilly*-extension of a monoid M is*-simple.
Proof.Let I be a*-ideal of BR*(M,θ)and(m,x,n)∈I.Then
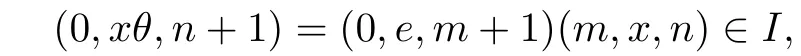
where e is the identity of M.Since xθH*e in M,we see that(0,e,0)and(0,xθ,n+1)are R*-related in BR*(M,θ)by Lemma 2.1 of[6].Thus(0,e,0)∈I and consequently I=S.
Theorem 2.1Let T be an ω-chain of cancellative monoids of length d.Then BR*(T,θ)is a*-simple type A ω2-semigroup with inf i nite D*-classes such that D*=~D and D*|ES=Md. Proof.Evidently,BR*(T,θ)is a type A monoid by Lemma 2.4 of[6],and by Lemma 2.2,it is*-simple.For two idempotents(m,fi,j,m)and(n,fk,l,n)in BR*(T,θ),(m,fi,j,m)>(n,fk,l,n)if and only if m<n or m=n and fi,j>fk,l.Thus the idempotents of BR*(T,θ)form an ω2-chain
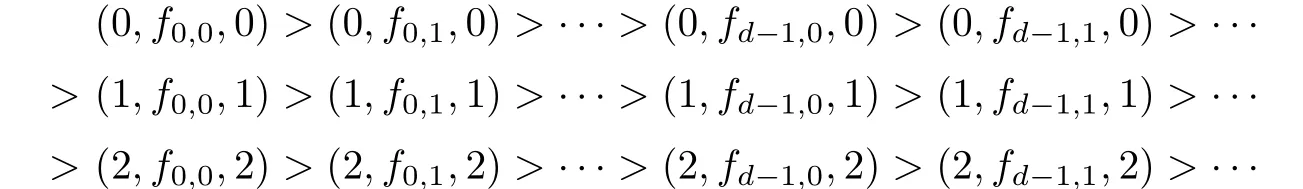
For any i,k,n∈N0such that 0≤k≤d-1,we write
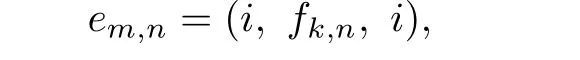
where m=id+k.Then the set of idempotents of S is{em,n:m,n∈N0}and em,n≤ep,qif and only if(m,n)≤(p,q).Thus S is an ω2-semigroup.For any em,n,ep,q∈ES,by(1.1 we have that(em,n,ep,q)∈D*if and only if m≡p(mod d)and n=q,and so S is *-simple type A ω2-semigroup in which D*|ES=Md.
Now if u=(m,x,n)∈BR*(T,θ),then x∈Ti,j,(i,j)∈D×N0,and by Lemma 2. of[6],uH*v where v=(m,fi,j,n)is a regular element.Thus each H*-class in BR*(T,θ contains a regular element.Hence D*=by Lemma 1.5.
To prove that there are inf i nite D*-classes,observe that
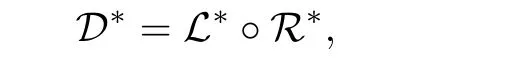
and if(m,x,n)L*uR*(h,y,k),where u=(p,z,q),then n=q,p=h and xL*(T)zR*(T)y. Ifandthen evidently
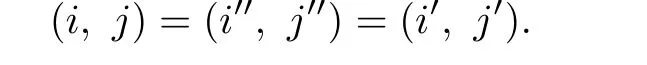
Hence a D*-class of BR*(T,θ)is contained in N0×Ti,j×N0for some(i,j)∈D×N0.On the other hand,a simple check shows that any two elements of N0×Ti,j×N0are D*-related. Thus a D*-class of BR*(T,θ)equals N0×Ti,j×N0,(i,j)∈D×N0.Therefore,there are inf i nite D*-classes of BR*(T,θ).
3 The Structure Theorem
This section is devoted to showing that any*-simple type A ω2-semigroup in which D*=~D and D*|ES=Mdis isomorphic to a semigroup of the type BR*(T,θ).
In this section,S denotes a*-simple type A ω2-semigroup with D*=and D*|ES=Md. We write

where em,n≤ep,qif and only if(m,n)≤(p,q).The following is important.
Lemma 3.1The following conditions are equivalent in S:
(i)(em,i,en,j)∈D*;
(ii)H*(m,i),(j,n)/=Ø;
(iii)m≡n(mod d)and i=j.
Proof.Since S is a type A semigroup with D*=,the(i)and(ii)are easily seen to be equivalent by Lemma 1.5.Let
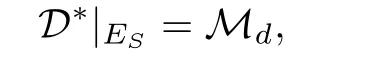
where S is a*-simple type A ω2-semigroup,and let
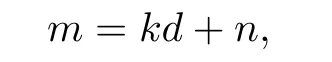
where k∈N0.Then we have(ekd+n,i,en,i)∈Md.Hence
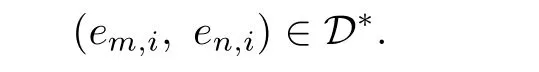

We adopt the convention that a0=e0,0.Thus,it is clear that an∈H*(0,0),(0,nd)for all n∈N0.Since e0,0RanLend,0,it is easy to verify that the inverse a-nof anis in H*(nd,0),(0,0)and that
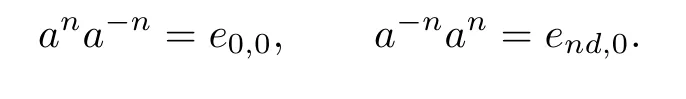
Lemma 3.2Every element of S is uniquely expressible in the form
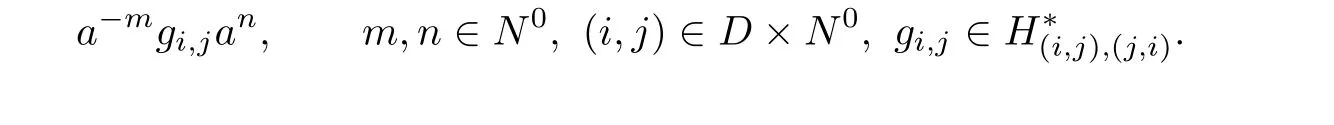
Proof.If z∈S,then by Lemma 3.1,for some p,x,y,q∈N0with x=y and p≡q(mod d).Let x=y=j.For i∈{0,1,···,d-1},let p≡q≡i(mod d),say


Also,since ee=e,ee=eand eze=z,it follows that

Observe that m,i,j and n are uniquely determined by p,x,y and q,and if,then
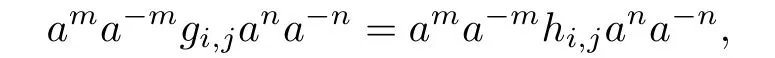
that is,
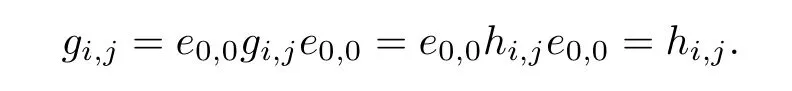
Theorem 3.1Let S be a*-simple type A ω2-semigroup with D*=D~ and D*|ES=Md. Then S is isomo∪rphic to a generalized Bruck-Reilly extension BR*(T,θ)of a monoid T, whereis an ω-chain of cancellative monoids of length d and θ is an endomorphism of T with image in T0,0.
Proof.Put
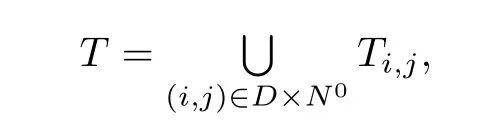
where
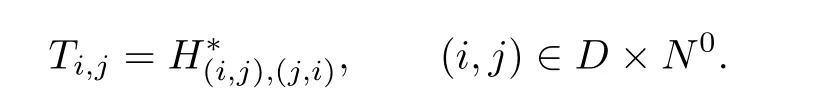
Then T is an ω-chain of cancellative monoids of length d,and the idempotents form a chain
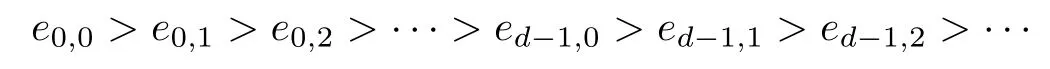
We adopt the above notation that a is a f i xed regular element in.If x∈T,then x∈Ti,jfor some(i,j)∈D×N0,and

Def i ne θ:T→T0,0by xθ=axa-1.Then for x,y∈T we have
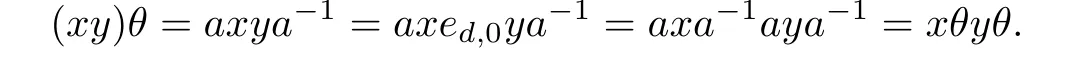
Furthermore,the image xθ is in the H*-class of e0,0,which enables us to show that S can be obtained as a generalized Bruck-Reilly extension BR*(T,θ)of T determined by the endomorphism θ.
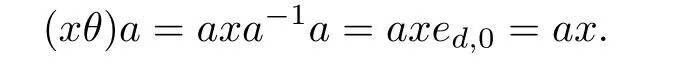
Now we show that
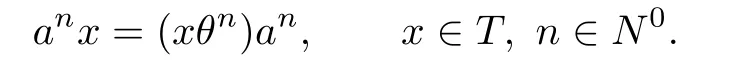
This holds trivially for n=0.Assume inductively that
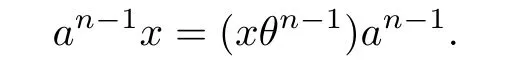
Then

Similarly,
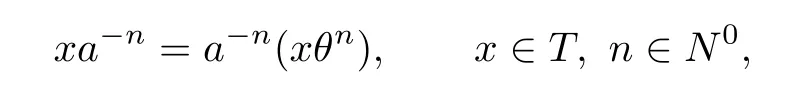
where
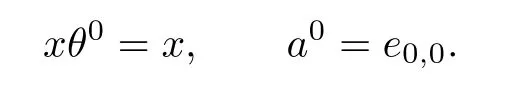
Let x,y∈T and m,n,p,q∈N0.If n≥p,since apa-p=a0=e0,0,then we have
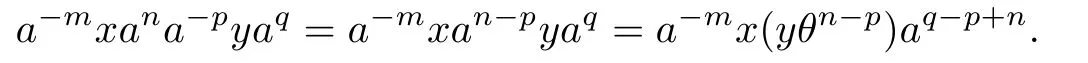
On the other hand,if n<p,then
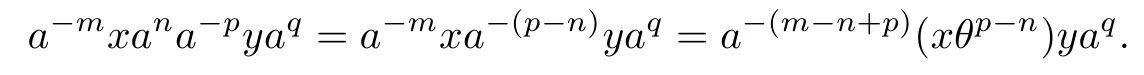
Put
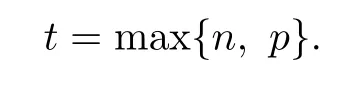
It is obvious that
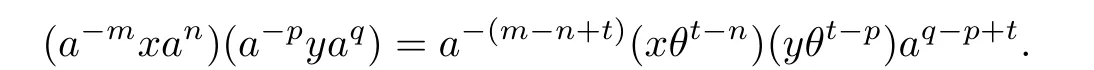
Def i ne a mapping ψ from S to BR*(T,θ)by

Then evidently ψ is a bijection and for s=a-mxan,t=a-pyaq,clearly,
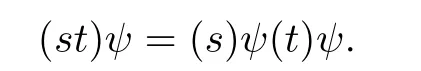
Hence ψ is an isomorphism from S onto BR*(T,θ).The proof of the theorem is then completed.
4 The Isomorphism Theorem
In this section we obtain a criterion for isomorphisms of two*-simple type A ω2-semigroups in which D*=and D*|ES=Md.
Let
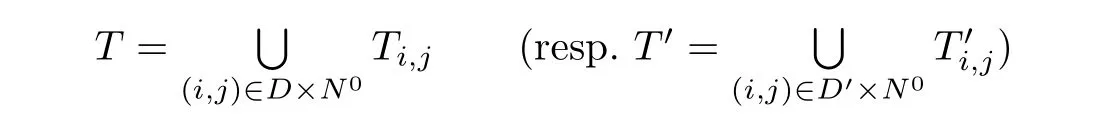
be ω-chains of cancellative monoids of length d(resp.with linking homomorphisms γ(i,j),(k,l)(resp.from Ti,jto Tk,l(resp.to T),where
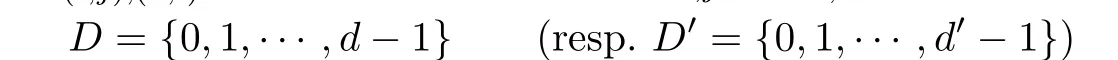
and
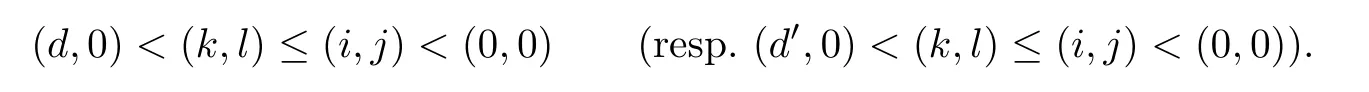
Let ei,j(resp.)be the identity of Ti,j(resp.).Then for(d,0)<(k,l)≤(i,j)≤(0,0) and ai,j∈Ti,jwe have
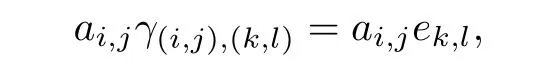
and for(d′,0)<(k,l)≤(i,j)≤(0,0)and∈,we have
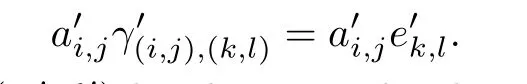
Let S=BR*(T,θ),S′=BR*(T′,θ′)be the generalized Bruck-Reilly extensions of T,T′, respectively.
Theorem 4.1The semigroups S,S′are isomorphic if and only if
(i)d=d′
and
(ii)there exist isomorphisms ψi,jof Ti,jonto,(i,j)∈D×N0and an inner automorphism τuofwhere u is a unit ofsuch that
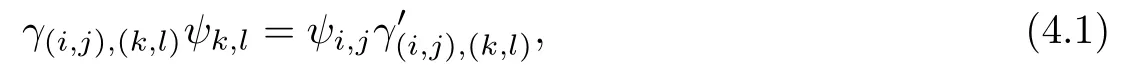
where(d,0)<(k,l)<(i,j)≤(0,0),and

where(d,0)<(k,l)≤(0,0).
Proof.Let σ:S→S′be an isomorphism.Then S and S′have the same number of D*-classes,so by Theorem 2.1,d=d′.
Now σ|ESis clearly an isomorphism of the chain ESonto ES′,so for m∈N0,(i,j)∈D×N0,
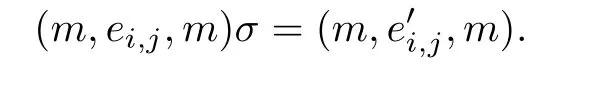
It follows that σ maps an H*-class of S onto an H*-class of S′.Hence we can def i ne a mapping ψ:T→T′by the rule that for all a∈T

Evidently,ψ is an isomorphism.Let
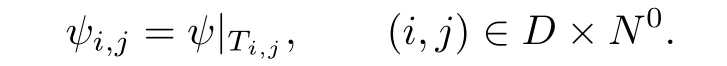
Then for(d,0)<(k,l)<(i,j)≤(0,0)and ai,j∈Ti,j,we have

and for bi,j∈also
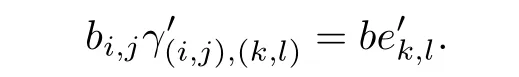
Using these facts we have that
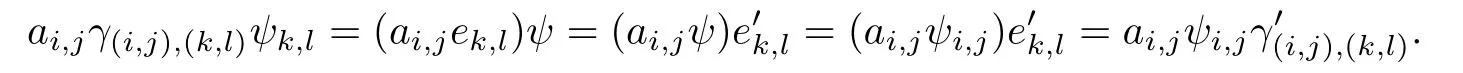
Hence,

Let
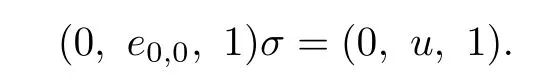
Since(0,e0,0,1)is regular,(0,u,1)is regular,and hence by Lemma 2.2 of[6]u is regular. But u∈,so u is a unit ofandexists.Let τube the inner automorphism of T′0,0def i ned by u.
For(d,0)<(k,l)≤(0,0)and ak,l∈Tk,l,we have ak,lθ∈T0,0and
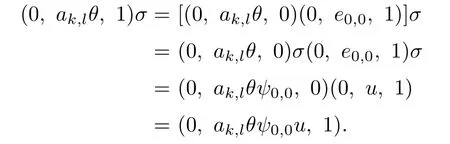
But
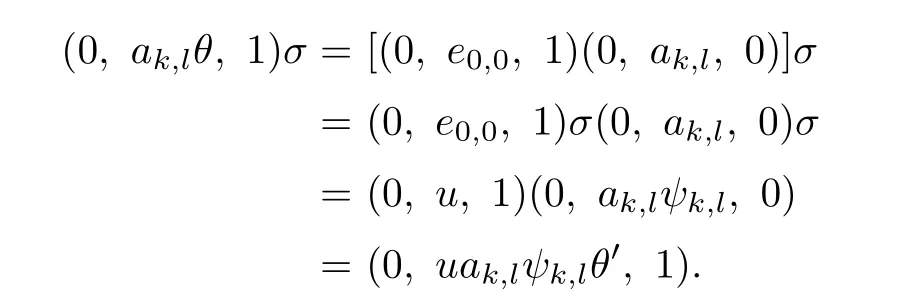
Hence,
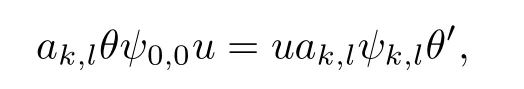
that is,

So
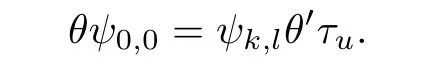
For the converse we f i rst def i ne ψ:T→T′by
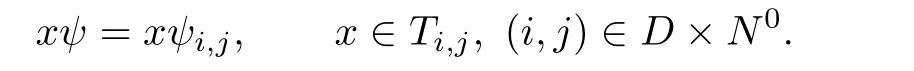
Clearly,ψ is an isomorphism.Let τube determined by the unit u of T′.Then for y in T′, we have
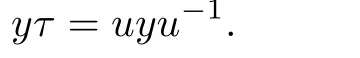
For each positive integer m,let
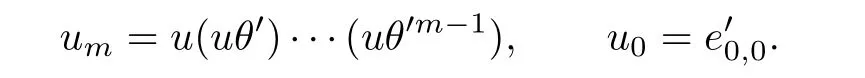
We claim that
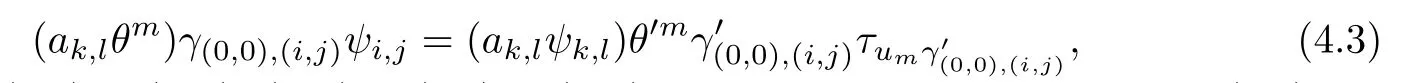
where(d,0)<(k,l)≤(0,0),(d,0)<(i,j)≤(0,0),ak,l∈Tk,land m∈N.Using(4.2),we obtain
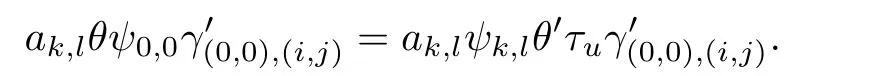
By virtue of(4.1)we have
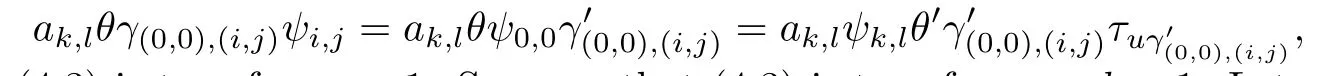
and thus(4.3)is ture for m=1.Suppose that(4.3)is ture for m=h-1.Let ak,l∈Tk,l. Then by(4.2)we have
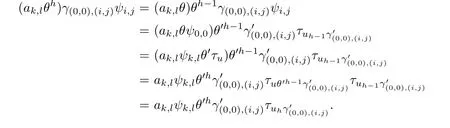
So(4.3)holds for each positive integer m by induction.
Clearly,umis in the group of units of T′,and so the mapping σ:S→S′def i ned by

is clearly one-one and onto.Let(m,ai,j,n),(p,ak,l,q)∈S.We show that
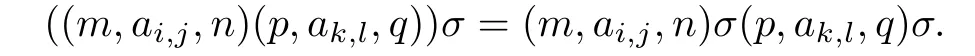
It is convenient to consider separately the f i ve cases:
(i)n=p,(i,j)=(k,l);
(ii)n=p,(i,j)<(k,l);
(iii)n=p,(i,j)>(k,l);
(iv)n>p;
(v)n<p.
Case(i).In this case,we have
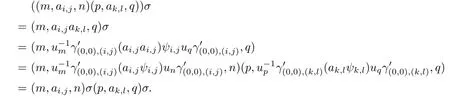
Case(ii).Utilizing(4.1),we obtain
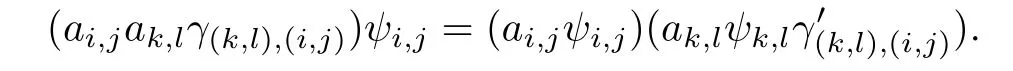
Thus we have
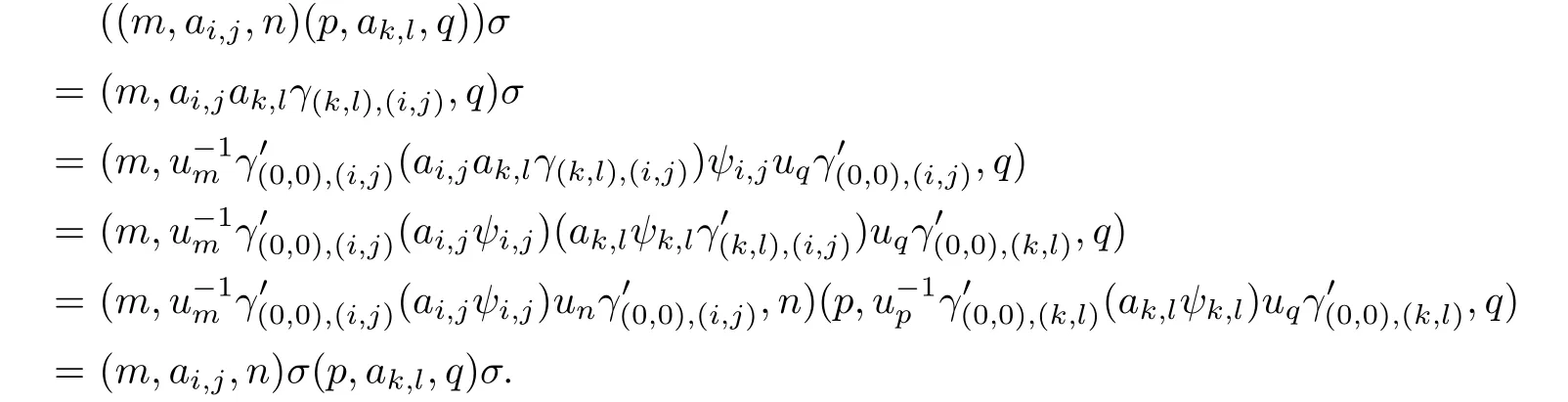
Case(iii).This is similar to case(ii)and we omit the details.
Case(iv).Using(4.3)we obtain
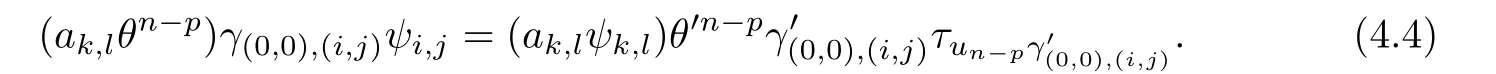
A straightforward calculation shows that
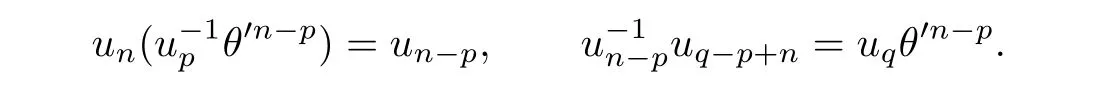
Thus
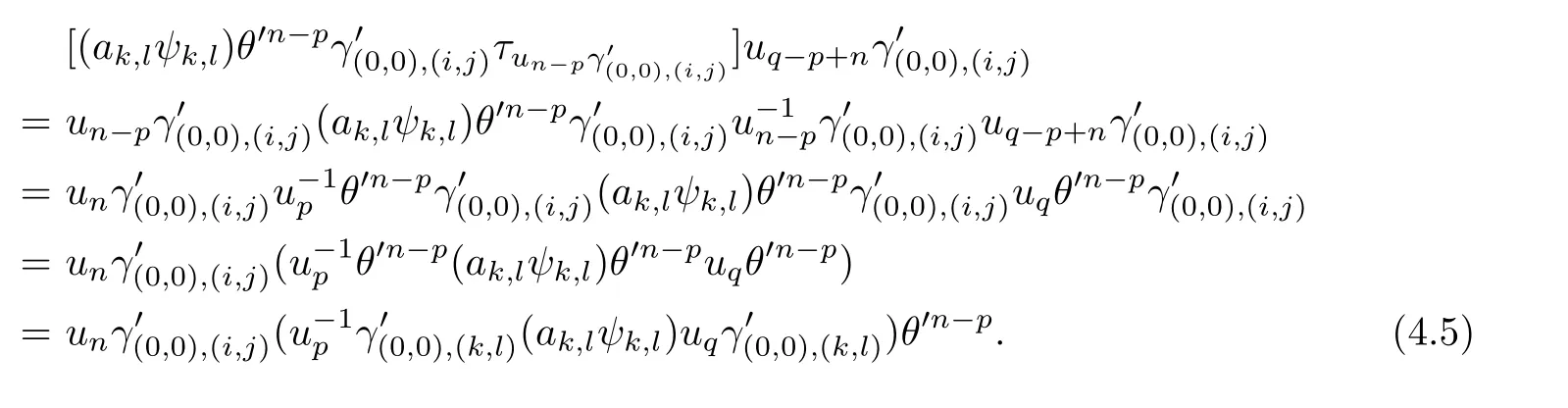
By virtue of(4.4)and(4.5)we have
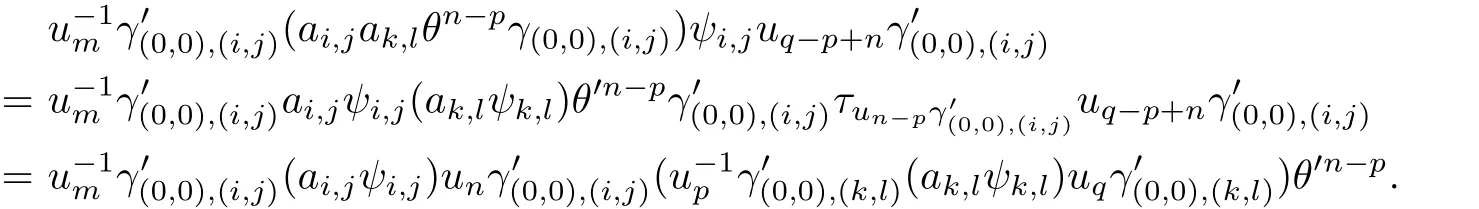
Thus,we have
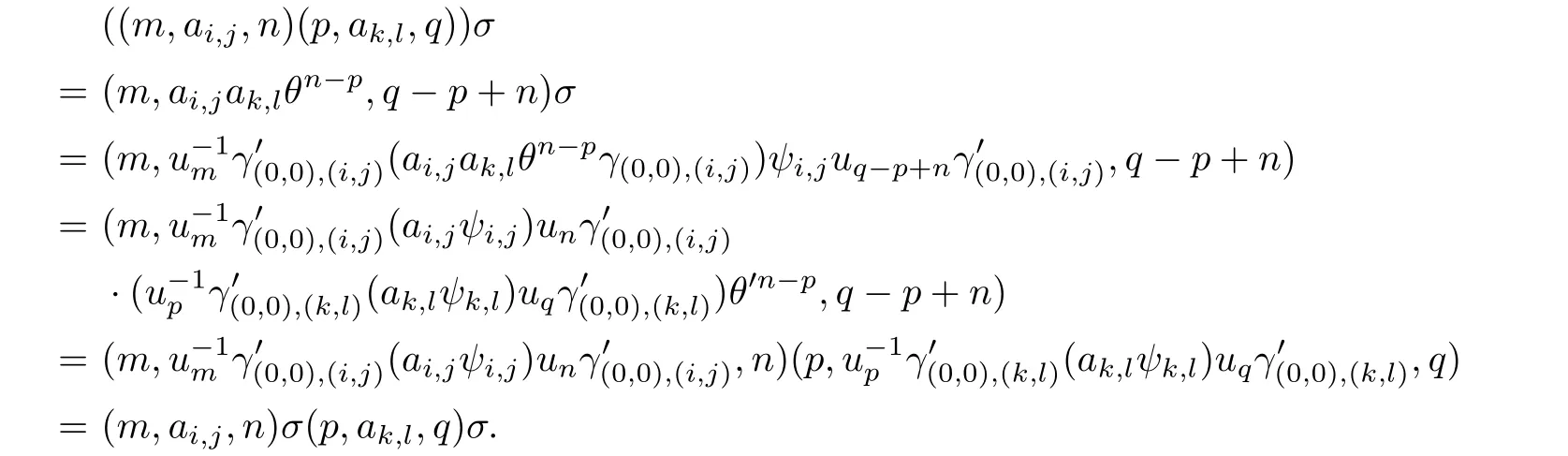
Case(v).This is similar to case(iv)and we omit the details.
The proof is completed.
[1]Shang Y,Wang L M.*-bisimple type A ω2-semigroups as generalized Bruck-Reilly*-extensions. Southeast Asian Bull.Math.,2008,32:343–361.
[2]Fountain J B.Abundant semigroups.Proc.London Math.Soc.,1982,44:103–129.
[3]Fountain J B.Adequate semigroups.Proc.Edinbourgh Math.Soc.,1979,28:113–125.
[4]Lawson M V.The natural partial order on an abundant semigroup.Proc.Edinburgh Math.Soc., 1987,30:169–186.
[5]Asibong-ibe U.*-simple type A ω-semigroups.Semigroup Forum,1993,47:135–149.
[6]Asibong-ibe U.*-bisimple type A ω-semigroups—I.Semigroup Forum,1985,31:99–117.
[7]Howie J M.Fundamentals of Semigroup Theory.Oxford:Clarendon Press,1995.
A
1674-5647(2013)03-0218-13
Received date:Nov.25,2010.
The NSF(10901134)of China and the Science Foundation(2011Y478)of the Department of Education of Yunnan Province.
E-mail address:shangyu503@163.com(Shang Y).
2000 MR subject classif i cation:20M10
 Communications in Mathematical Research2013年3期
Communications in Mathematical Research2013年3期
- Communications in Mathematical Research的其它文章
- On the Expected Present Value of Total Dividends in a Risk Model with Potentially Delayed Claims
- An Evolving Random Network and Its Asymptotic Structure
- The Supersolvable Order of Hyperplanes of an Arrangement
- The Centres of Gravity of Periodic Orbits
- Modelling the Spread of HIV/AIDS Epidemic
- A Family of Fifth-order Iterative Methods for Solving Nonlinear Equations
