On the Expected Present Value of Total Dividends in a Risk Model with Potentially Delayed Claims

XIE JIE-HUAAND ZOU WEI

(1.School of Economics and Trade,Nanchang Institute of Technology,Nanchang,330099) (2.Department of Science,Nanchang Institute of Technology,Nanchang,330099)

Communicated by Wang De-hui

On the Expected Present Value of Total Dividends in a Risk Model with Potentially Delayed Claims

XIE JIE-HUA1AND ZOU WEI2,*

(1.School of Economics and Trade,Nanchang Institute of Technology,Nanchang,330099) (2.Department of Science,Nanchang Institute of Technology,Nanchang,330099)

Communicated by Wang De-hui

In this paper,we consider a risk model in which two types of individual claims,main claims and by-claims,are def i ned.Every by-claim is induced by the main claim randomly and may be delayed for one time period with a certain probability. The dividend policy that certain amount of dividends will be paid as long as the surplus is greater than a constant dividend barrier is also introduced into this delayed claims risk model.By means of the probability generating functions,formulae for the expected present value of total dividend payments prior to ruin are obtained for discrete-type individual claims.Explicit expressions for the corresponding results are derived for Knclaim amount distributions.Numerical illustrations are also given.

compound binomial model,delayed claim,dividend,expected present value

1 Introduction

The barrier strategy was initially proposed by De Finetti[1]for a binomial risk model.More general barrier strategies for a risk process have been studied in a number of papers;for example,see[2–7]and references therein.The main focus is on optimal dividend payouts and problems associated with time of ruin,under various barrier strategies and other economic conditions.In fact,the study on risk models with dividend payments has been one of the major interests in the risk theory literature.

In reality,insurance claims may be delayed due to various reasons.Since the work by Waters and Papatriandafylou[8],risk models with this special feature have been discussed by many authors in the literature.For example,Yuen and Guo[9]studied a compound binomial model with delayed claims and obtained recursive formulas for the f i nite time ruin probabilities.Xiao and Guo[10]also studied this risk model and derived an upper bound for the ruin probabilities.Xie and Zou[11]studied the ultimate ruin probability for a risk model with delayed claims,and exact analytical expressions for the ruin functions were obtained. Yuen et al.[12]studied a risk model with delayed claims,in which the time of delay for the occurrence of a by-claim is assumed to be exponentially distributed.A framework of delayed claims is built by introducing two kinds of individual claims,namely,main claims and byclaims,allowing possible delays of the occurrences of by-claims.All risk models described above relied on the assumption that each main claim induces a by-claim to a certainty.

Motivated by these works,in this paper,we consider a compound binomial risk model with delayed claims and dividend payments that are ruled by a constant barrier.In our model,every by-claim is induced by the associated main claim randomly.It is obvious that the incorporation of the randomness of delayed claim and dividend payments makes the problem more interesting.It also complicates the analysis of the risk model.We use the technique of generating functions to calculate the expected present value of total dividends for this risk model.The paper is structured as follows:In Section 2,we def i ne the model of interest,describes various payments,including the premiums,claims and dividends,and lists the notations.In Section 3,dif f erential equations with certain boundary conditions are developed for the expected present value of total dividend payments prior to ruin.Then a general formula which allows us to evaluate the expected present value of the total discounted dividends is derived by using the technique of generating functions.Moreover,closed-form solutions for the expected present value of dividends are obtained for Knclaim size distributions in Section 4.Numerical examples are also provided to illustrate the applicabilities of our main results and the ef f ects of the delay of claims on the expected present value of dividends in Section 4.

2 Model Description and Notations

Here,we consider a discrete time model which involves two types of insurance claims,i.e., the main claims and the by-claims.Denote the discrete time units by k=0,1,2,···In any time period,the probability of having a main claim is q,0＜q＜1.The occurrences of main claims in dif f erent time periods are independent.It is assumed that each main claim induces a by-claim with probability φ,0＜φ＜1,and the main claim does not induce a by-claim with probability 1-φ.Moreover,if the main claim induces a by-claim,then the by-claim and its associated main claim may occur simultaneously with probability θ,or the occurrence of the by-claim may be delayed to the next time period with probability 1-θ. All claim amounts are independent,positive and integer valued.The main claim amounts X1,X2,···are independent and identically distributed(i.i.d.).Put X=X1.Then thecommon probability function(c.p.f.)of the Xiis given by

The corresponding probability generating function(p.g.f.)and the mean are

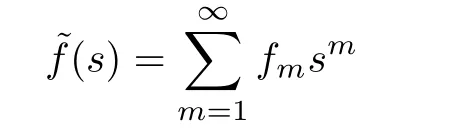
and

respectively.Let Y1,Y2,···be i.i.d.by-claim amounts and put Y=Y1.Denote their c.p.f. by

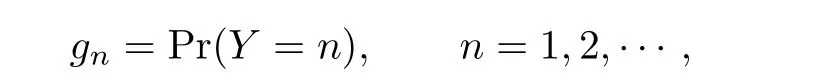
and write the p.g.f.and the mean asandµY,respectively.

Let Skbe the total amount of claims up to the end of the kth time period,k∈N+and S0=0.We def i ne

Assume that premiums are received at the beginning of each time period with a constant premium rate of 1 per period,and all claim payments are made only at the end of each time period.We introduce a dividend policy to the company that certain amount of dividends will be paid to the policyholder instantly,as long as the surplus of the company at time k is higher than a constant dividend barrier b(＞0).It implies that the dividend payments is only possibly occur at the beginning of each period,right after receiving the premium payment.The surplus at the end of the nth time period,Ub(n),is then def i ned to be

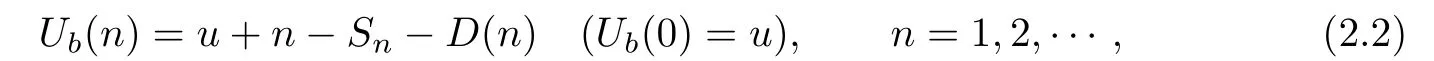
where D(n)is the sum of the total dividend payments in the f i rst n periods,with the def i nition

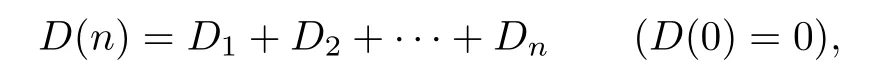
and

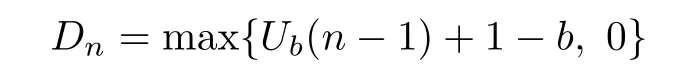
being the amount of dividend paid out at the end of period n.Here the initial surplus is u, u=0,1,···,b.

The positive safety loading condition holds if q(µX+φµY)＜1.Def i ne

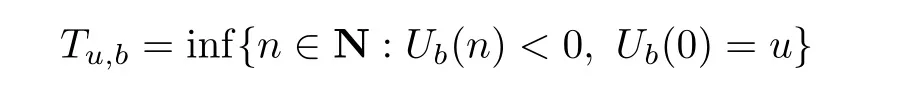
to be the time of ruin.Let v be a constant annual discount rate for each period.Then the expected present value of the dividend payments due until ruin is

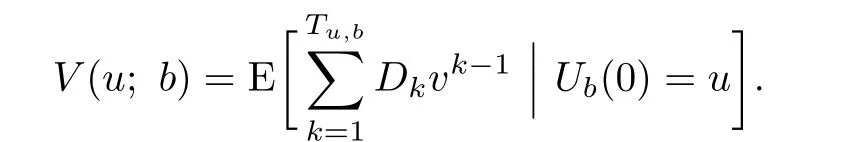
3 Main Results

To study the expected present value of the dividend payments,V(u;b),we need to study the claim occurrences in three scenarios.

(1)If a main claim occurs in a certain period and does not induce a by-claim,then the surplus process gets renewed expect for the initial value;

(2)If a main claim induces a by-claim and they occur concurrently in some period,then there will be no by-claim in the next time period and the surplus process also gets renewed expect for the initial value;

(3)If a main claim occurs in some period and induces a by-claim,but the by-claim is delayed to the next period,then the surplus process behaves dif f erently because of the delayed by-claim occurring in the forthcoming period.

Conditioning on the third scenario,that is,the main claim occurred in the previous period and induced a by-claim,but the by-claim will occur at the end of the current period, we def i ne the corresponding surplus process as

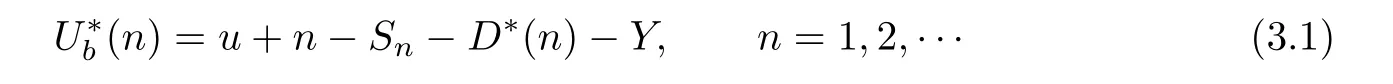
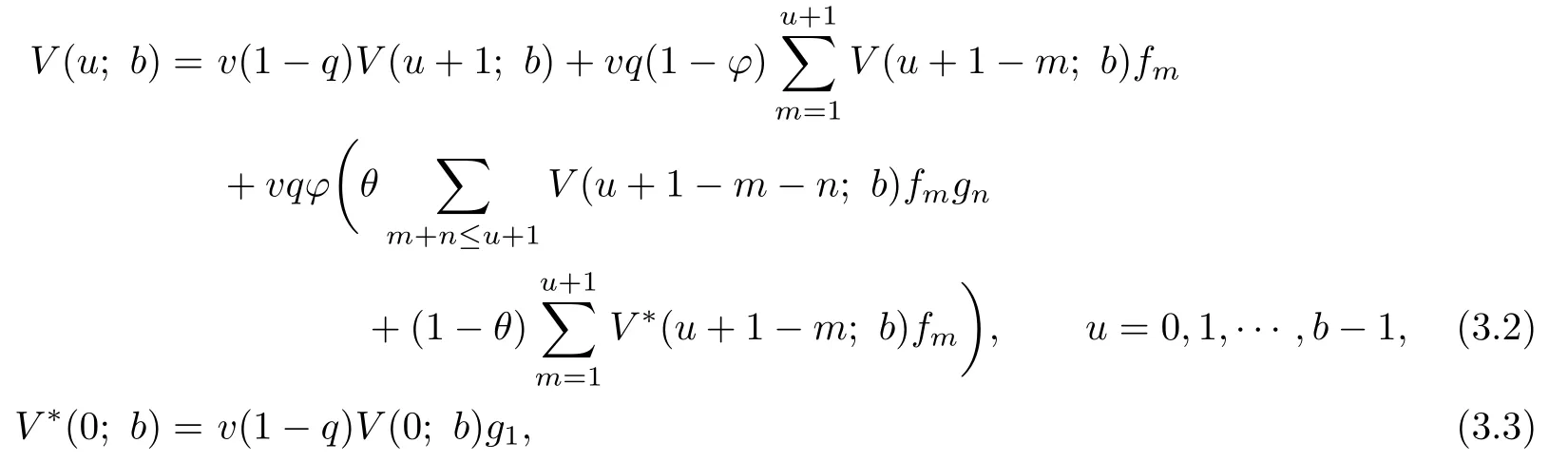
and for u=1,2,···,b-1,

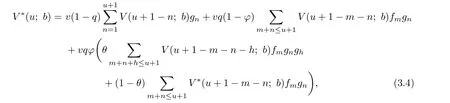
with the boundary condition

The boundary condition holds because when the initial surplus is b,the premium received at the beginning of the f i rst period will be paid out as a dividend immediately.Except the fi rst dividend payment,the rest of the model is the same as that starting from an initial surplus b-1.From(3.2)and(3.4)we can rewrite V*(u;b)as

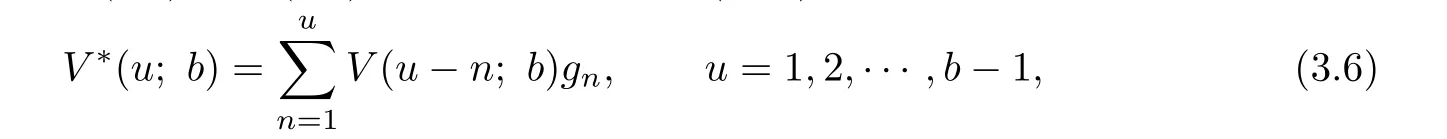
Substituting(3.6)into(3.2)gives

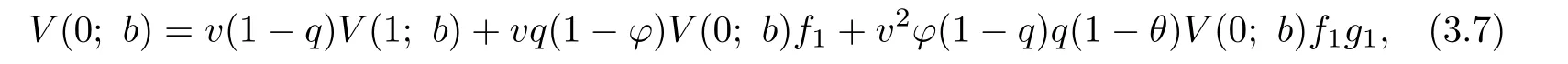
and for u=1,2,···,b-1,

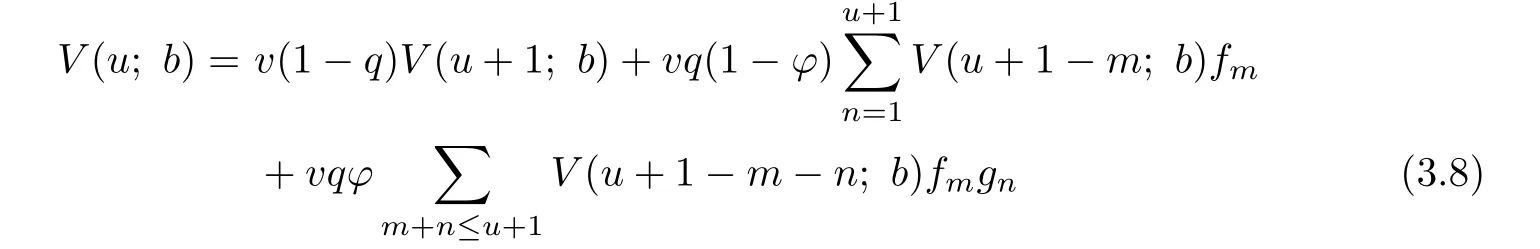
with the boundary condition(3.5).

To obtain an explicit expression for V(u;b)from(3.7)and(3.8),we def i ne a new function W(u)that satisf i es the following dif f erence equations:

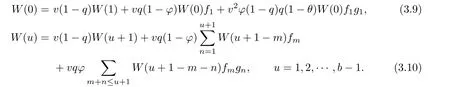
Aparting from a multiplicative constant,the solution of(3.9)and(3.10)is unique.Therefore, we can set W(0)=1.It follows from the theory of dif f erence equations that the solution to (3.7)and(3.8)with the boundary condition(3.5)is of the form

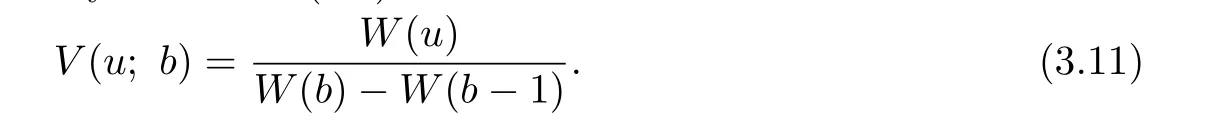
We now apply the tool of generating functions to f i nd the particular solutions W(u)to the particular equation(3.10).

Let the generating function of W(u)be

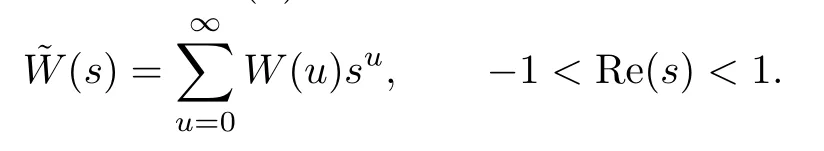
Similarly,

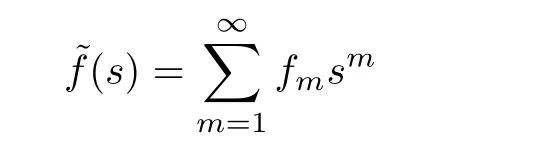
and

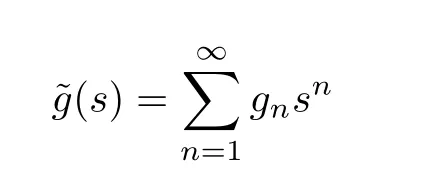
are probability generating functions ofand,respectively.Furthermore, we construct two new generating functions

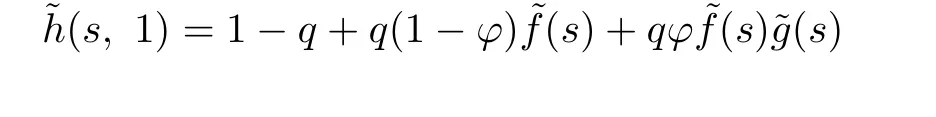
and

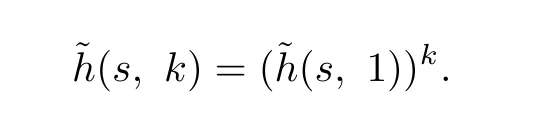
We denote the probability function of˜h(s,k)by h(i,k).In the following theorem,we show that V(u;b)can be expressed explicitly in terms of h(i,k).

Theorem 3.1For the expected present value of dividend payments V(u;b)of the model (2.2),we have

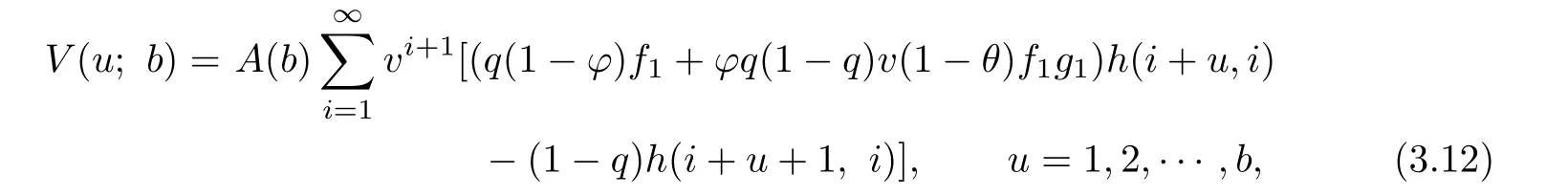
where

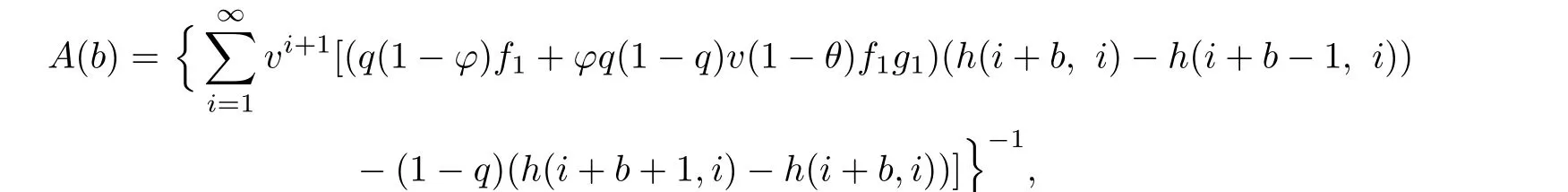
and V(0;b)=A(b).

Proof.The result(3.12)can be derived by using the technique of generating functions. Multiplying both sides of(3.10)by zuand summing over u from 1 to∞,we get

From(3.9)and the fact that W(0)=1,the above equation is simplif i ed to

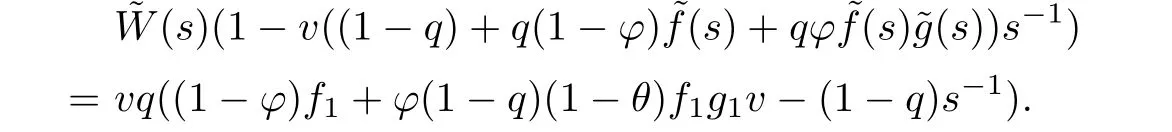
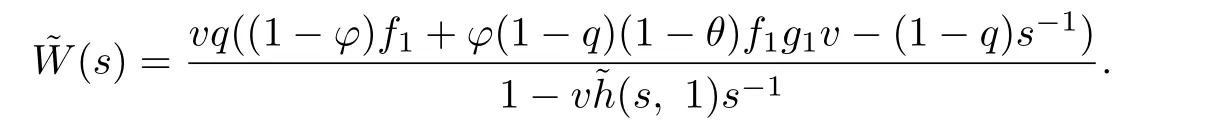
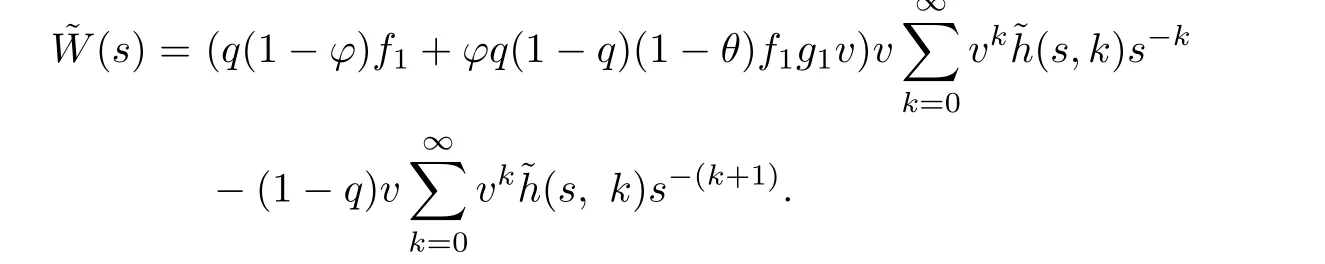
Comparing the coefficients of suin both sides gives,for u=1,2,···,b,we get

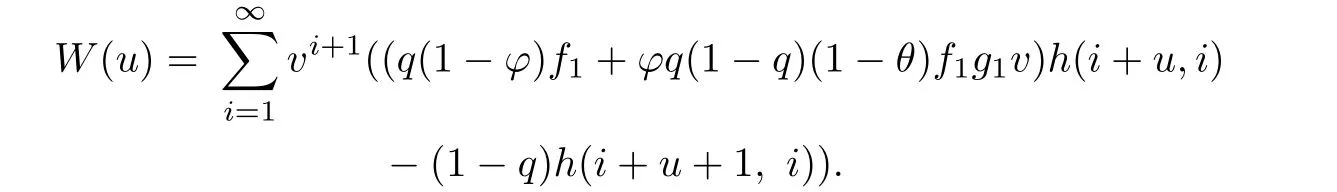
The above result together with(3.11)gives us the explicit expression for V(u;b).This completes the proof.

4 Explicit Expressions

Kndistributions include geometric,negative binomial,and discrete phase-type,as well as their linear combinations(including mixtures).We give the explicit results for expected present value of dividends when the claims from both classes are Kndistributed in this section.

For two independent claim amount random variables X1and Y1,if they have Kndistributions,so does their sum.Therefore,in this section,we assume that fx=Pr(X1=x)and gx=Pr(Y1=x)are Khdistributed and Kldistributed,respectively,for x=1,2,···,and h,l=1,2,···,i.e.,

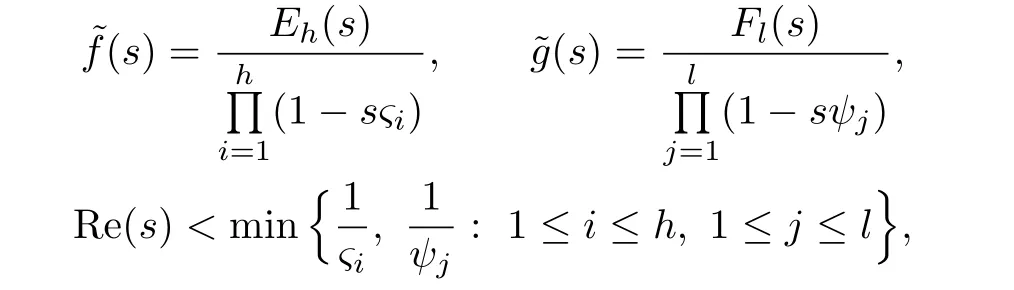
where 0＜ςi＜1,0＜ψj＜1,for i=1,2,···,h,j=1,2,···,l,Eh(s)is a polynomial of degree h with

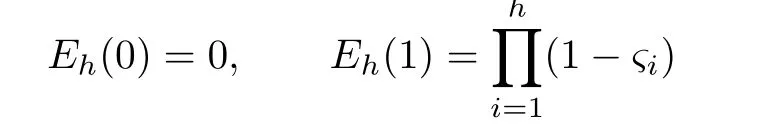
and Fl(s)is a polynomial of degree l with

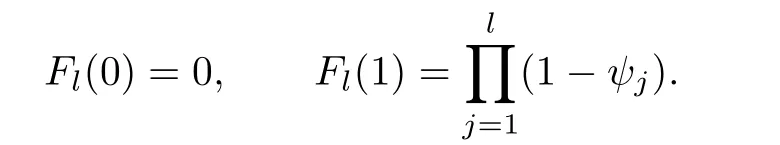
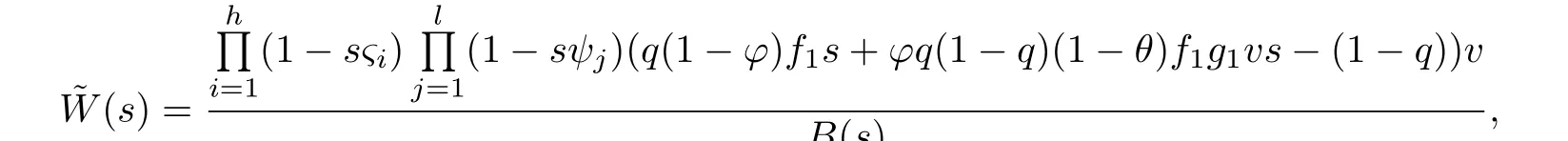
where

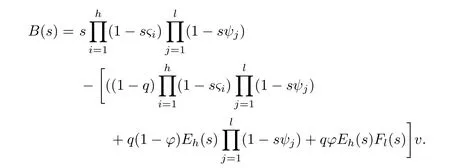
Since the denominator of the above equation is a polynomial of degree h+l+1,it can be factored as,where R1,R2,···,Rh+l+1are the h+l+1 zeros of the denominator.We remark

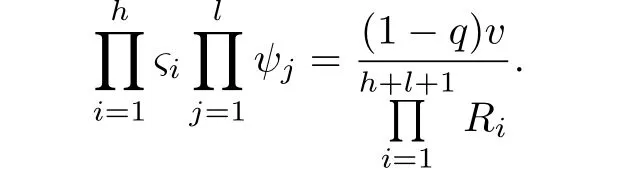
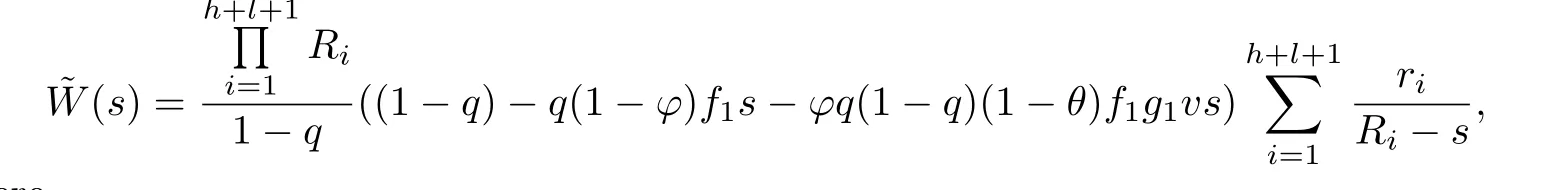
where

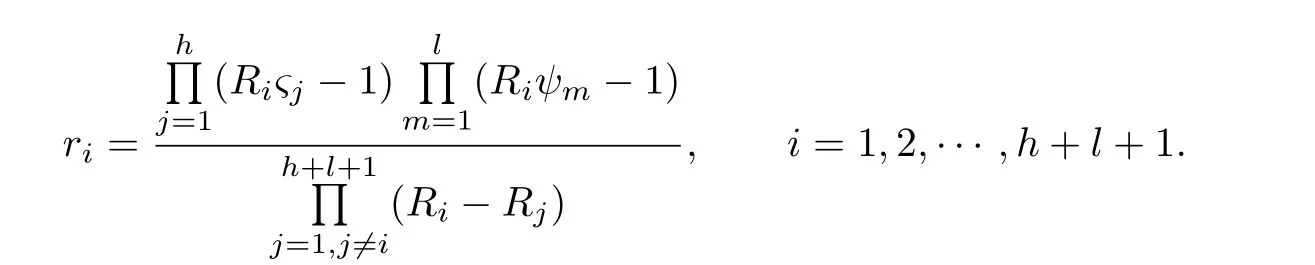
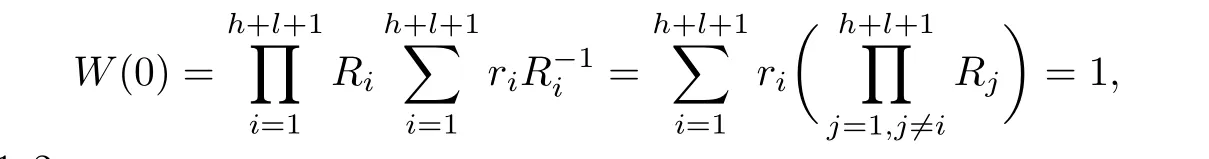
and for u=1,2,···,

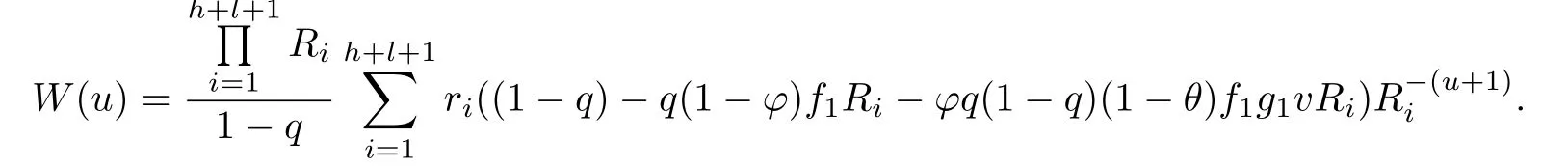
Now,we know that

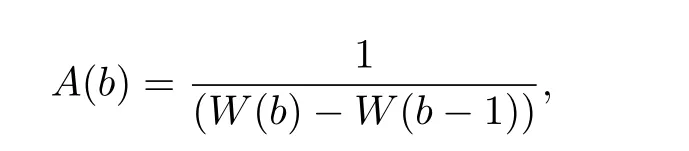
and then f i nally we have

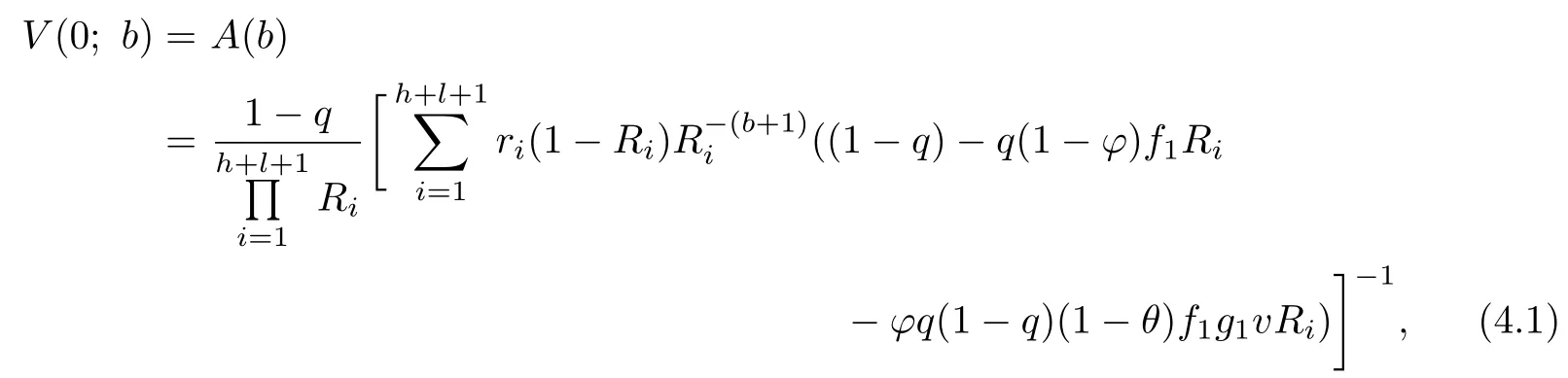
and for u=1,···,b,

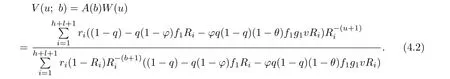
Example 4.1In this example,we assume that the main claim X1follows a geometric distribution with

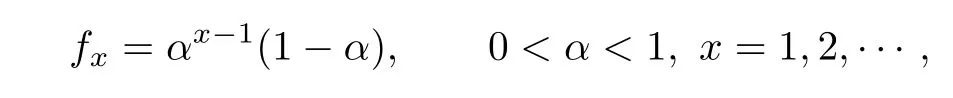
and the by-claim Y1follows a geometric distribution with

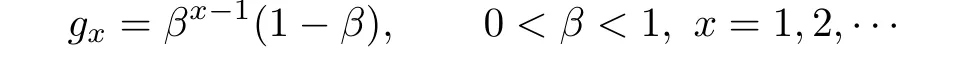
So

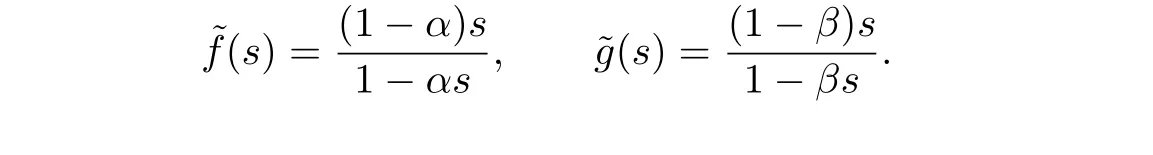
Here h=l=1,ς1=α,ψ1=β and Eh(s)=(1-α)s,Fl(s)=(1-β)s.Let R1,R2,R3be the three roots of the equation

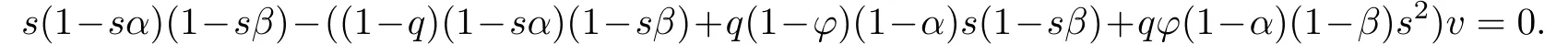
Then we have

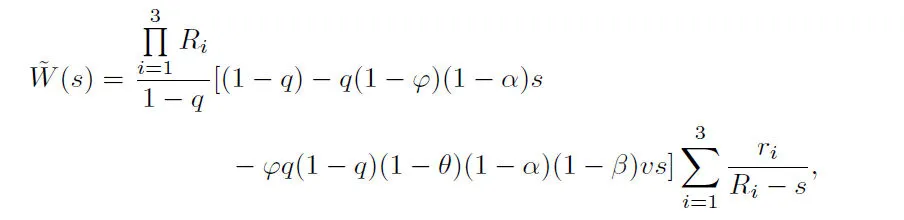
where

Then(4.1)and(4.2)are simplif i ed to

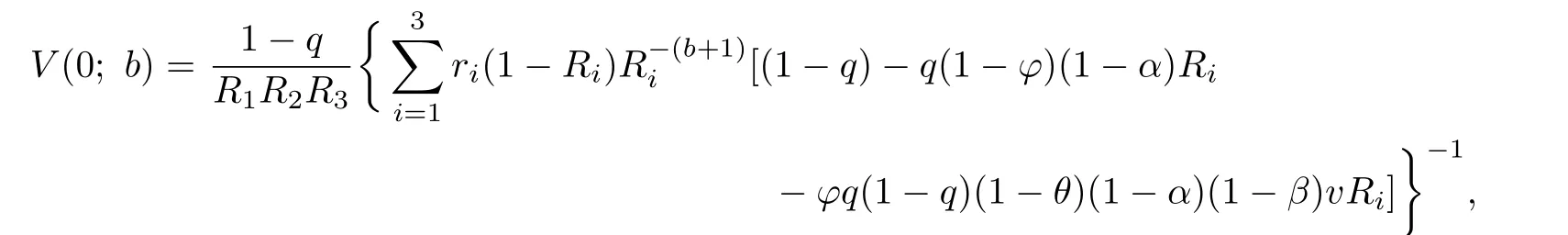
and for u=1,···,b,

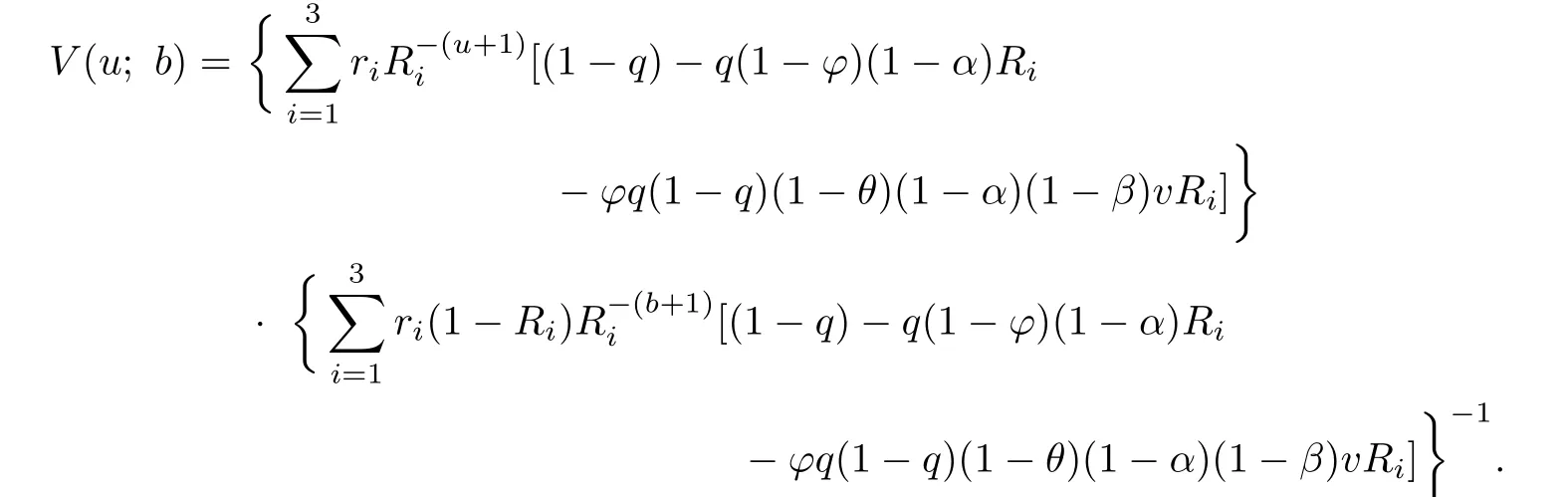
Let q=0.35,φ=0.95,v=0.95,b=10,α=β=0.8.From the above results we get R1=0.64425,R2=1.01868,R3=1.47015,r1=0.75939,r2=-0.20258,and r3=0.08319. The values of V(u;10)for θ=0,0.25,0.5,0.75,1 and u=1,···,10 are listed in Table 4.1.

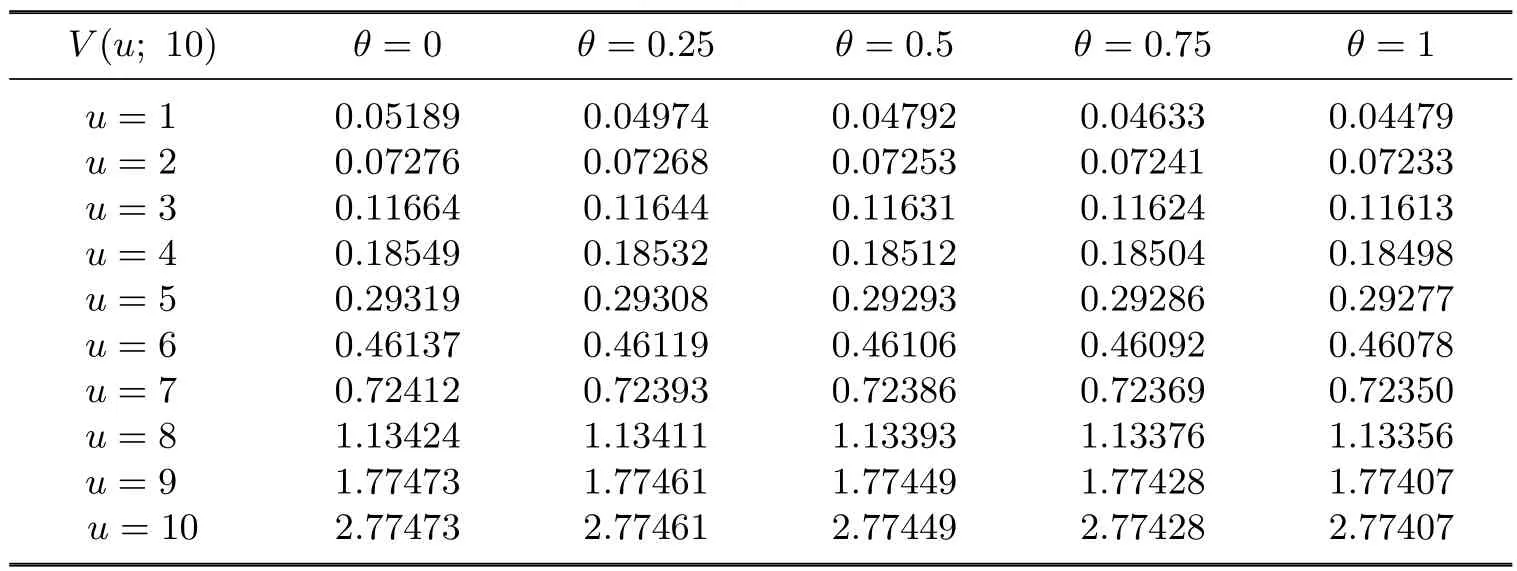
Table 4.1Values of V(u;10)for geometric distributed claims

We observe the features that V(u;b)is an increasing function with respect to u,and a decreasing function over θ.Also,the impact of the delay of by-claims on the expected present value of dividends is reduced for a higher initial surplus of the company.

[1]De Finetti B.Su Un’impostazione Alternativa Dell Teoria Collettiva del Rischio.in:Peter F M.Transactions of the XVth International Congress of Actuaries.vol.2.New York:The Econometric Society,1957:433–443.

[2]Claramunt M M,Mˊarmol M,ALEGRE A.A note on the expected present value of dividends with a constant barrier in the discrete time model.Bull.Assoc.Suisse Actuaires,2003,2: 149–159.

[3]Dickson D C M,Waters H R.Some optimal dividends problems.Astin Bull.,2004,34:49–74.

[4]Gerber H U,Shiu E S W.Optimal dividends:analysis with Brownian motion.N.Am.Actuar. J.,2004,8:1–20.

[5]Li S,Garrido J.On a class of renewal risk models with a constant dividend barrier.Insurance Math.Econom.,2004,35:691–701.

[6]Frosting E.On the expected time to ruin and the expected dividends when dividends are paid while the surplus is above a constant barrier.J.Appl.Probab.,2005,42:595–607.

[7]Bara K,Hwa-sung K,Jeongsim K.A risk model with paying dividends and random environment.Insurance Math.Econom.,2008,42:717–726.

[8]Waters H R,Papatriandafylou A.Ruin probabilities allowing for delay in claims settlement. Insurance Math.Econom.,1985,4:113–122.

[9]Yuen K C,Guo J Y.Ruin probabilities for time-correlated claims in the compound binomial model.Insurance Math.Econom.,2001,29:47–57.

[10]Xiao Y T,Guo J Y.The compound binomial risk model with time-correlated claims.Insurance Math.Econom.,2007,41:124–133.

[11]Xie J H,Zou W.Ruin probabilities of a risk model with time-correlated claims(in Chinese). J.Grad.Sch.Chinese Acad.Sci.,2008,3,319–326.

[12]Yuen K C,Guo J Y,Ng K W.On ultimate ruin in a delayed-claims risk model.J.Appl. Probab.,2005,42:163–174.

A

1674-5647(2013)03-0193-10

Received date:March 22,2009.

The NSF(11201217)of China and the NSF(20132BAB211010)of Jiangxi Province.

*Corresponding author.

E-mail address:jhxie@nit.edu.cn(Xie J H),zouwei@nit.edu.cn(Zou W).

2000 MR subject classif i cation:62P05,91B30