A Family of Fifth-order Iterative Methods for Solving Nonlinear Equations

LIU TIAN-BAOAND CAI HUA

(1.School of Mathematics,Jilin University,Changchun,130012) (2.Fundamental Department,Aviation University of Air Force,Changchun,130022)

Communicated by Li Yong

A Family of Fifth-order Iterative Methods for Solving Nonlinear Equations

LIU TIAN-BAO1,2AND CAI HUA1,*

(1.School of Mathematics,Jilin University,Changchun,130012) (2.Fundamental Department,Aviation University of Air Force,Changchun,130022)

Communicated by Li Yong

In this paper,we present and analyze a family of f i fth-order iterative methods free from second derivative for solving nonlinear equations.It is established that the family of iterative methods has convergence order f i ve.Numerical examples show that the new methods are comparable with the well known existing methods and give better results in many aspects.

Newton’s method,iterative method,nonlinear equation,order of convergence

1 Introduction

In this paper,we consider the iterative methods to f i nd a simple root α of a nonlinear equation

i.e.,f(α)=0 and f′(α)/=0,where f:I⊂R→R for an open interval I is a scalar function. Newton's method is an important and basic approach for solving nonlinear equations(see [1]),and its formulation is given by

This method converges quadratically.To increase the order of convergence of the iterative methods,many authors have developed new methods(see[2–11]).

A two-step predictor-corrector Householder method(see[12])is given by

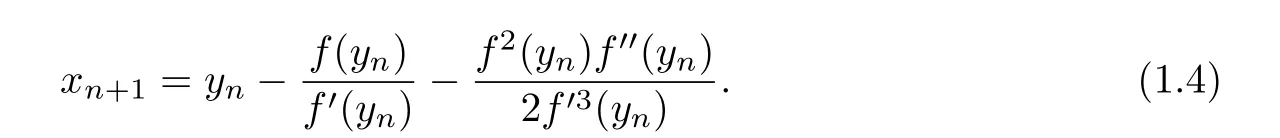
It is observed that the method depends on second derivative,so its practical utility is restricted rigorously.Therefore,it is important and interesting to develop iterative methods which are free from second derivative and whose order is higher if possible.This is main motivation of this paper.

2 Development of Methods and Convergence Analysis

Let us consider approximating the equation(1.1)around the point(xn,f(xn))by the equation

We impose the condition

on(2.1).From(2.1)-(2.2)we get the value of b easily determined in terms of a:

Then

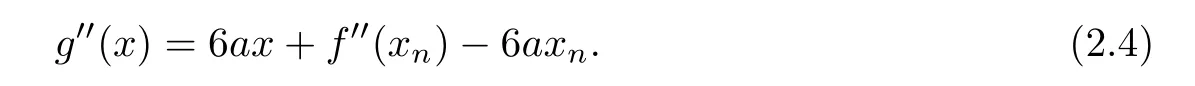
By(1.3)and(2.4),we have

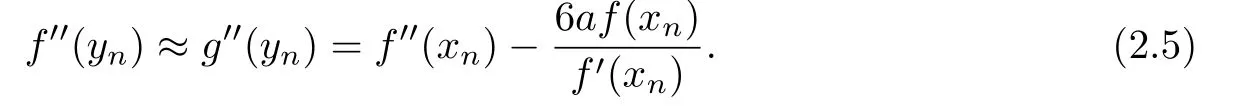
We consider

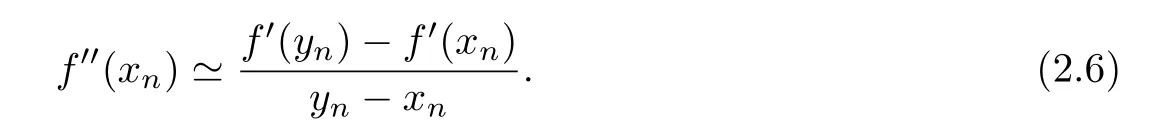
Combining(1.3)-(1.4)and(2.5)-(2.6),we obtain the following new family iterative method for solving(1.1).

Algorithm 2.1

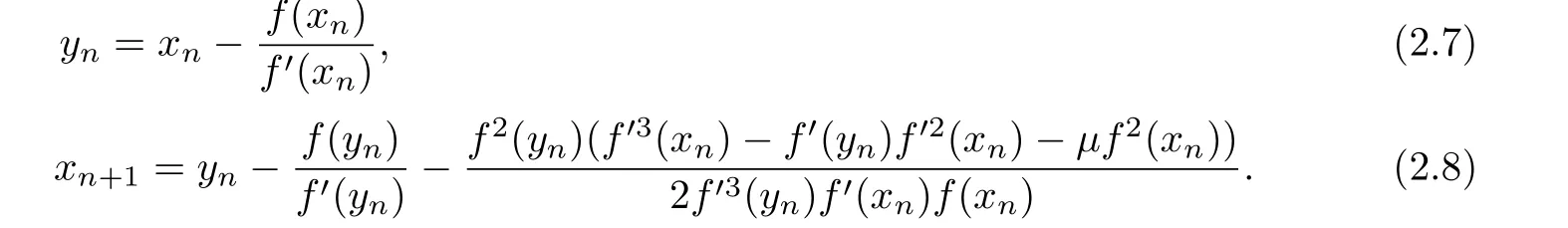
Theorem 2.1Let α∈I be a simple zero of sufficiently dif f erentiable function f:I⊂R→R for an open interval I.If x0is sufficiently close to α,then Algorithm 2.1 has fi fth-order convergence.

Proof.Let

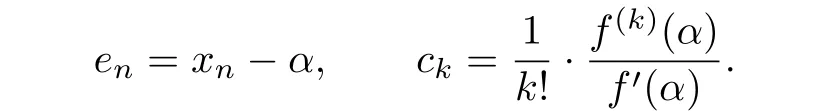
We use Taylor expansions as follows:

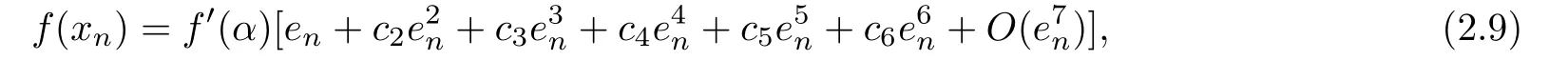
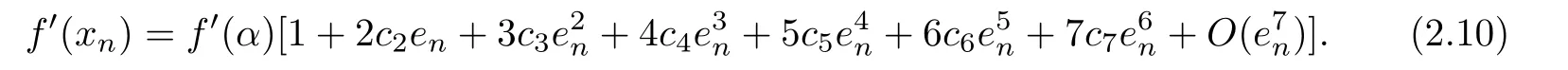
From(2.9)-(2.10)we get

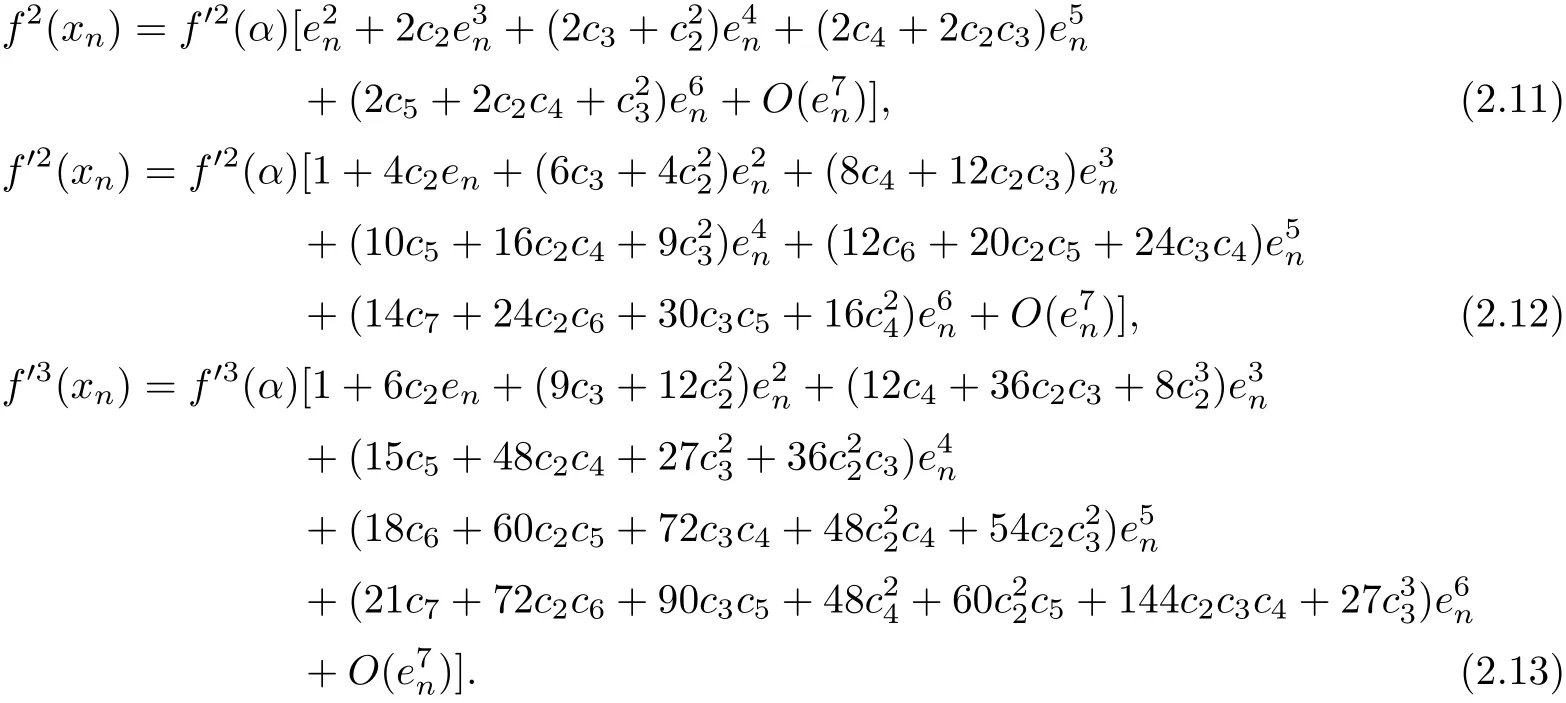
By using(2.9)-(2.10),we obtain

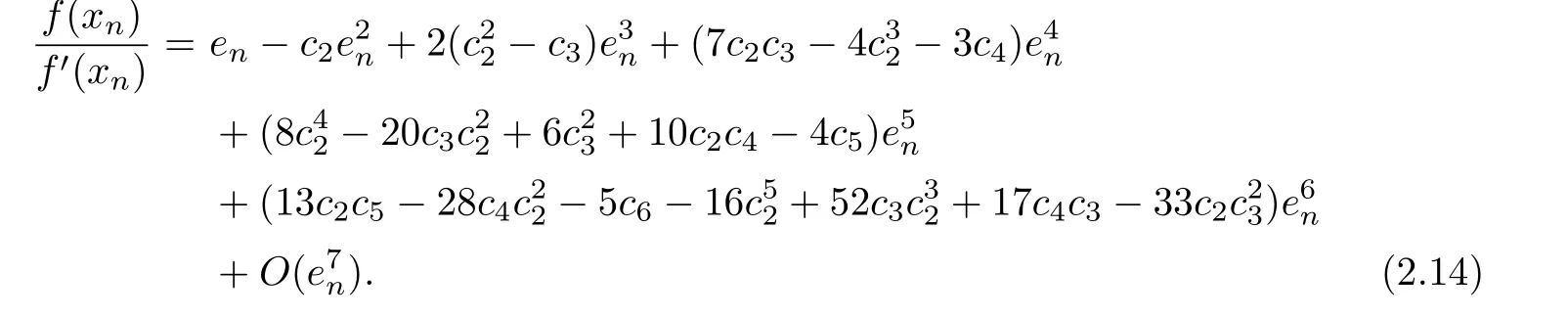
Then

By using the Taylor expansions for f(yn)at xn=α,we have

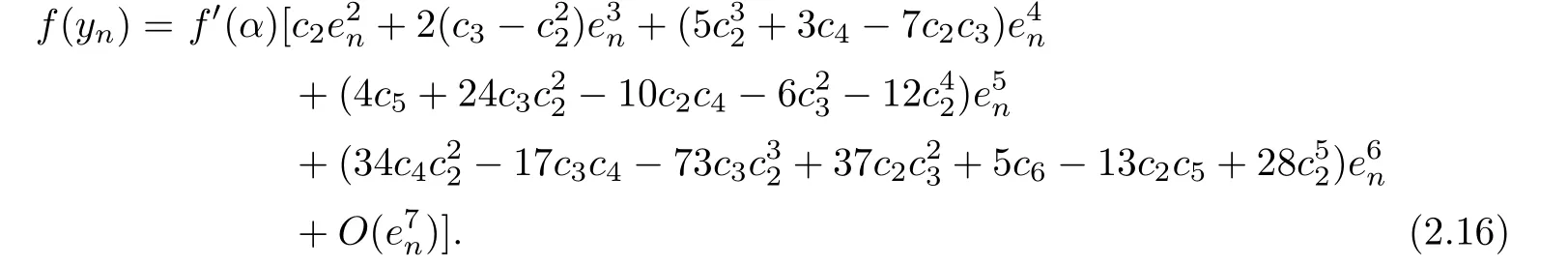
Then we obtain

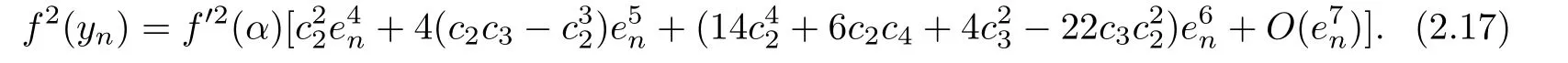
Similarly,we have

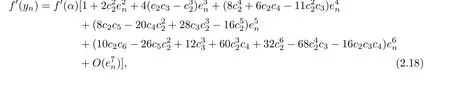
and

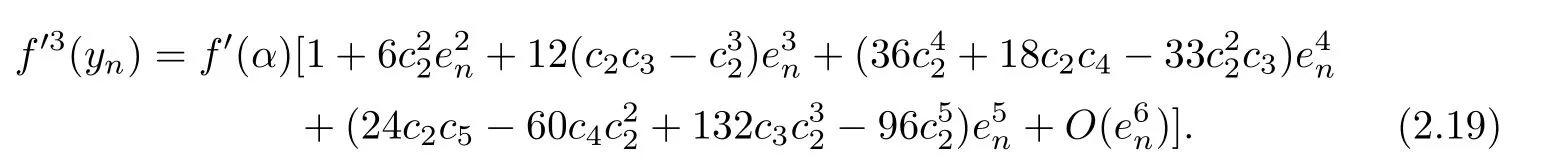
By using(2.12)and(2.18),we have

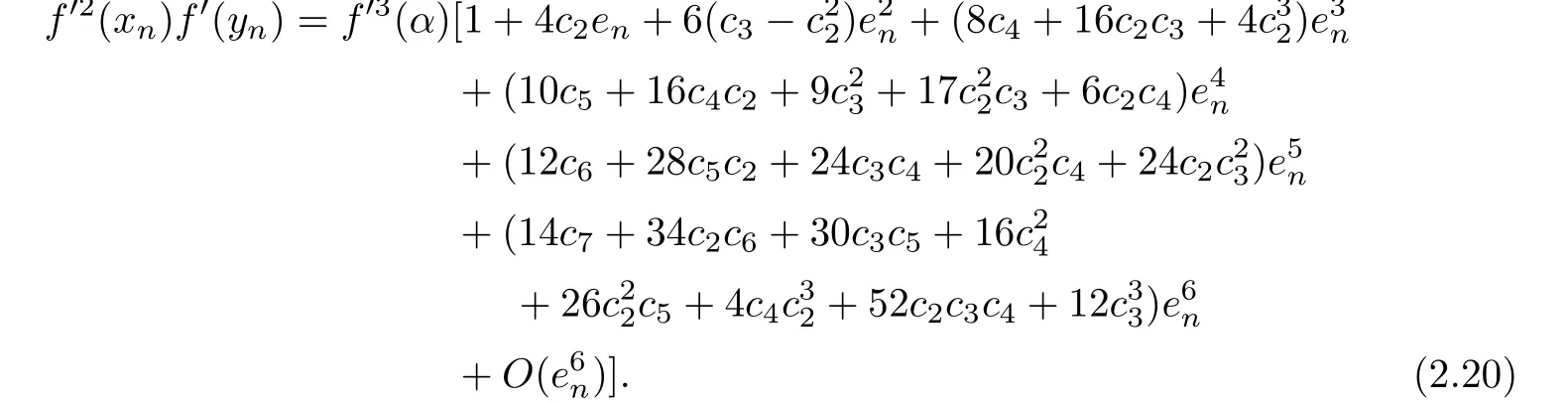
From(2.9),(2.10)and(2.19),we have

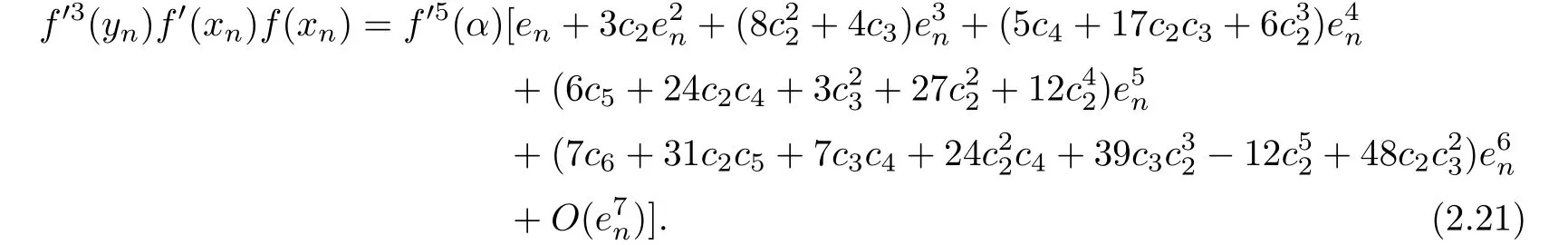
By using(2.16)and(2.18),we have

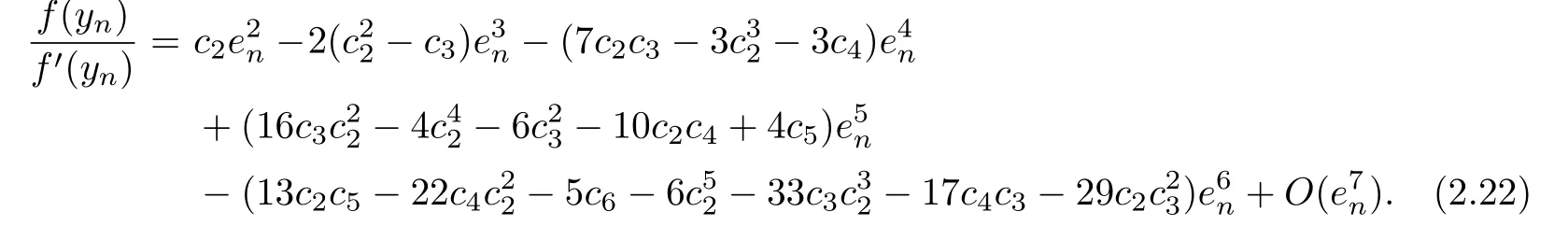
Substituting(2.11),(2.13)–(2.15),(2.17)and(2.20)–(2.22)into(2.8),we get

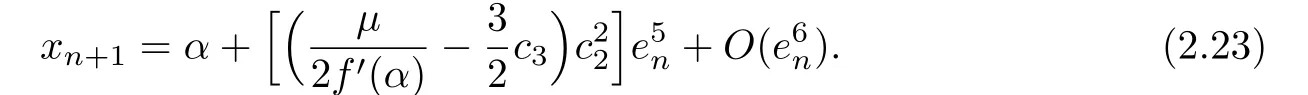
From

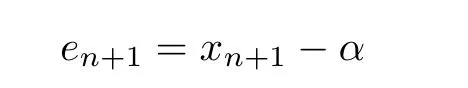
we have the error equation:

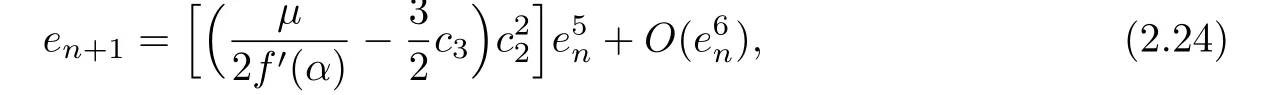
which shows that Algorithm 2.1 is of f i fth-order convergence.

3 Numerical Examples

We present some numerical test results for various f i fth-order iterative methods in Table 3.1. From the table,the following methods are compared:the Newton method(NM),the method of Noor and Noor[5](NR1),Noor and Khan[6](NR2),and Algorithm 2.1.We chooseµwith dif f erent values,and obtain dif f erent methods:µ=0(LM1),µ=1(LM2),µ=-1(LM3), µ=2(LM4).All computations were done by using Matlab 7.1.We accept an approximate solution rather than the exact root,depending on the precision∊of the computer.We use the following stopping criteria for computer programs:|f(xn+1)|＜∊,and the f i xed stopping criterion∊=10-15.

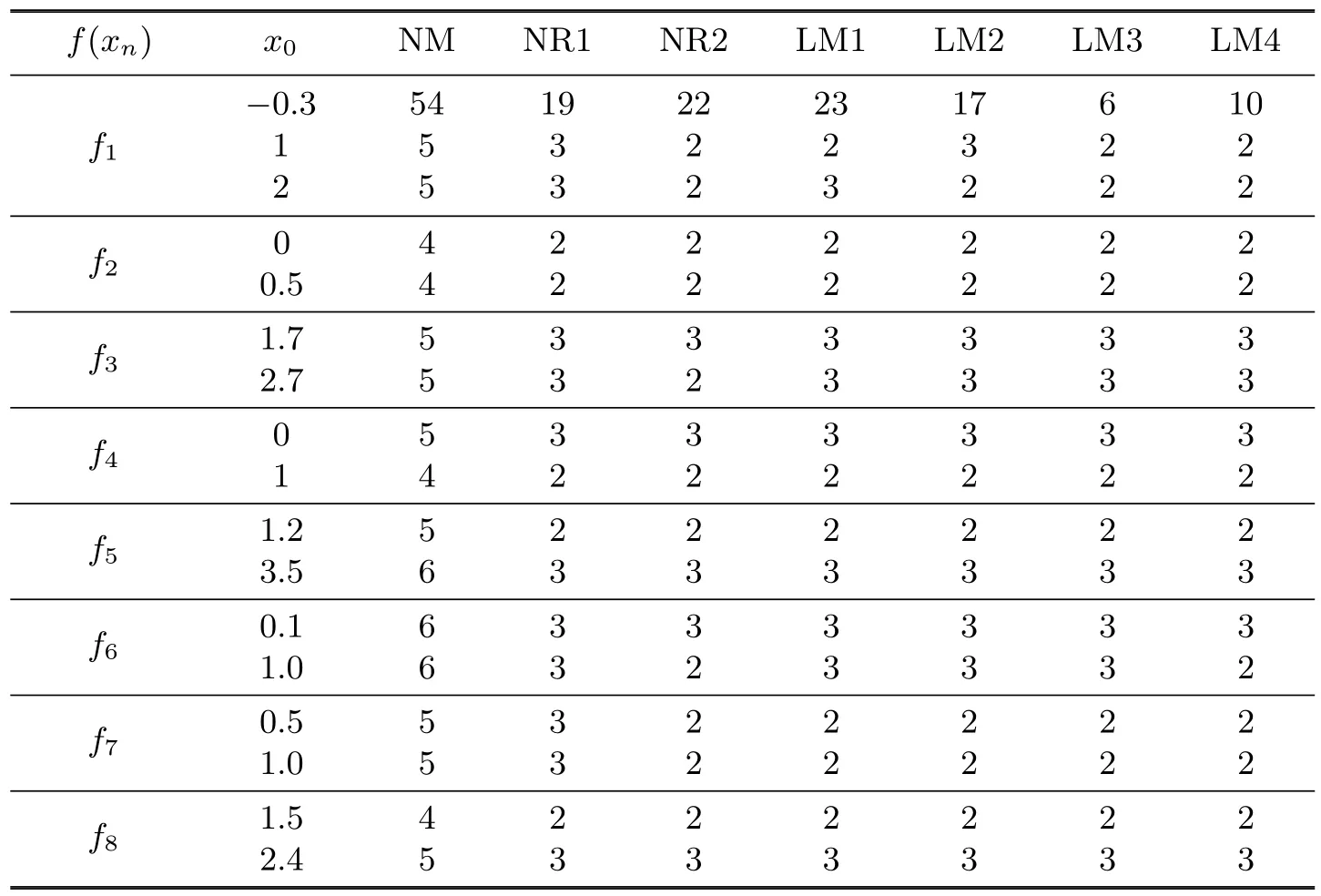
Table 3.1 Comparison of various f i fth-order methods and Newton’s method

We use some test functions and display the computed approximate zero x*as follows.

4 Conclusion

In this paper,we presented a family of f i fth-order iterative methods free from second derivative for solving nonlinear equations.We observed from numerical examples that the proposed methods have at least equal performance as compared with the other methods of the same order.

[1]Ostrowski A M.Solution of Equations in Euclidean and Banach Space.San Diego:Academic Press,1973.

[2]Argyros I K,Cho Y J,Hilout S.On the midpoint method for solving equations.Appl.Math. Comput.,2010,216:2321–2332.

[3]Cordero A,Hueso J L,Martˊınez E,Torregrosa J R.Efficient high-order methods based on golden ratio for nonlinear systems.Appl.Math.Comput.,2011,217:4548–4556.

[4]Khattri S K,Argyros I K.Sixth order derivative free family of iterative methods.Appl.Math. Comput.,2011,217:5500–5507.

[5]Noor M A,Noor K I.Fifth-order iterative methods for solving nonlinear equations.Appl. Math.Comput.,2007,188:406–410.

[6]Noor M A,Khan W A,Hussain A.A new modif i ed Halley method without second derivatives for nonlinear equation.Appl.Math.Comput.,2007,189:1268–1273.

[7]Kou J,Li Y,Wang X.A family of f i fth-order iterations composed of Newton and third-order methods.Appl.Math.Comput.,2007,186,1258–1262.

[8]Kou J,Li Y.The improvements of Chebyshev-Halley methods with f i fth-order convergence. Appl.Math.Comput.,2007,188:143–147.

[9]Noor M A.Numerical Analysis and Optimization.Lecture Notes,Mathematics Department, COMSATS Institute of Information Technology,Pakistan:Islamabad,2006.

[10]Householder A S.The Numerical Treatment of a Single Nonlinear Equation.New York: McGraw-Hill,1970.

[11]Chun C.Some variants of Chebyshev-Halley methods free from second derivative.Appl.Math. Comput.,2007,191:193–198.

[12]Noor K I,Noor M A,Momani S.Modif i ed Householder iterative method for nonlinear equations.Appl.Math.Comput.,2007,190:1534–1539.

A

1674-5647(2013)03-0255-06

Received date:Sept.14,2011.

*Corresponding author.

E-mail address:liutianbao27@126.com(Liu T B),caihua@jlu.edu.cn(Cai H).

2000 MR subject classif i cation:41A25,65D99