基于小波分析的脉搏波信号处理

徐洁

（徐州医学院 麻醉学院，江苏 徐州 221004）

人体脉搏信号是一种微弱信号，信噪比较低。在检测和采集时，由于受仪器、人体等方面的影响，所采集的信号中常存在如下3种噪声：1）基线漂移、人体呼吸等低频干扰，频率小于1 Hz；2）由于肢体抖动、肌肉紧张而引起的干扰，它的频率范围较大；3）工频干扰，是固定频率的干扰，频率为50 Hz。

这些干扰信号会极大的影响对脉搏信号进行进一步的识别与分析；因此，在对脉搏信号进行进一步处理之前必须对噪声进行处理，过去常常采用快速傅里叶变换或者数字滤波器等方法进行去噪，去噪结果容易产生相位失真，对脉搏波信号的去噪效果并不好。由于脉搏波信号属于非平稳信号，而小波变换具有多分辨率的特点，因此，采用小波分析能够较好的处理脉搏波等非平稳信号。基于小波变换的信号去噪方法，一般有阈值法、平移不变量法和模极大值法[1]。

1 小波变换阈值法去噪原理

小波阈值降噪的基本思想是：用如下模型代表一个含噪声的一维信号：

其中 s（t）为原始信号，n（t）为服从 N（0，σ2）的高斯白噪声。根据式（1），对f（t）作离散小波变换，因为正交小波变换具有很强的数据相关性，进行小波变化时，它能够把信号的能量集中在一些大的有限的系数中，而噪声的能量却分布于整个小波域内，变换后f（t）的小波系数一部分为信号对应的小波系数，另一部分为噪声对应的小波系数；并且幅值比较大的小波系数一般以信号为主，而幅值较小的系数在很大程度上是噪声。总体上来讲，对f（t）进行小波分解后，信号的系数要大于噪声的系数，这样就可以选择一个合适的临界阈值λ，如果分解后得到的系数大于这个临界阈值λ时，就认为此时的分解系数主要是由信号引起的，就保留这个系数（硬阈值方法）或者按照某一固定量向零收缩（软阈值方法）这个系数，如果分解系数小于这个临界阈值λ，就认为此时的分解系数主要是由噪声引起的，直接舍弃分解系数；经过这一步骤后，用得到的小波系数进行小波重构，就能去除噪声信号 n（t）[3]。

小波阈值法的主要步骤如下：

1）计算含噪声信号的正交小波变换。选择合适的小波和小波分解层数j，将含噪信号进行小波分解至j层，得到相应的小波分解系数。

2）对分解得到的小波系数进行阈值处理，其阈值的处理方法有2种：

其中s表示阈值处理后的信号，t表示阈值。

3）进行小波逆变换。将经阈值处理过的小波系数进行重构，得到去噪后的信号。分解后的信号如果不做阈值处理，则重构后的信号仍为原信号。用阈值函数进行处理并重构后，将得到去噪后的信号，这个信号经过小波处理后，去除了噪声，逼近于原始信号。

在小波阈值方法中，阈值的选取至关重要，选用不同的阈值，滤波信噪比将有明显的差别。若阈值太大，则信号细节损失太多，有可能会造成信号失真；而阈值太小，则达不到预期的去噪效果[4]。虽然阈值选取方法不少，如常用的固定门限阈值、Stein无偏似然法估计阈值、启发式阈值和最小最大准则门限阈值等[5]，但是阈值的选取不是一个简单问题，它需考虑抑制无用噪声与保留信号细小变化之间的权衡问题。

图1为一段含噪的脉搏波信号，采用阈值法对其进行降噪处理，在matlab7.0平台上，经过反复仿真，选择db9小波进行八层分解。

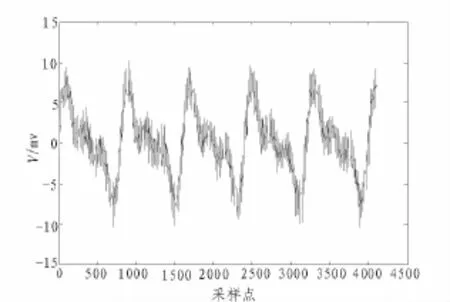
图1 一段含噪脉搏波Fig.1 Pulse-wave signal with noise

图2 小波阈值法去噪结果Fig.2 De-noising result of threshold method

经过小波阈值处理后得到的信号波形如图2所示，直观上可以看出噪声得到了比较好的抑制；但是，在脉搏波交替的地方出现较大的上、下峰值，这些峰值并不是原始脉搏波本身所包含的，而是在去噪的过程中产生的人为干扰，这种现象类似于Fourier去噪时所产生的伪吉布斯现象。

要避免伪吉布斯现象，可以采用小波平移不变量去噪法。

2 小波平移不变量去噪法

小波平移不变量去噪法即在一定的平移量范围内对所获得的信号按某一个平移量进行平移，获得一个在时域上与原始信号具有一定相位差的信号，然后对这个信号进行去噪处理，得到去噪后的信号，对该信号做反向的平移，则得到与原始信号同相位的信号，然后按另一个平移量进行平移——去噪——反平移，重复这一过程，对所获得结果求平均，就得到带噪信号去噪后的估计信号。这就是基于平移不变的小波阈值去噪的思想[6]。

采用平移不变量法对图1的原始脉搏波进行去噪处理，得到波形图如图3所示，从图中可以看出伪吉布斯现象得到了很好的抑制。

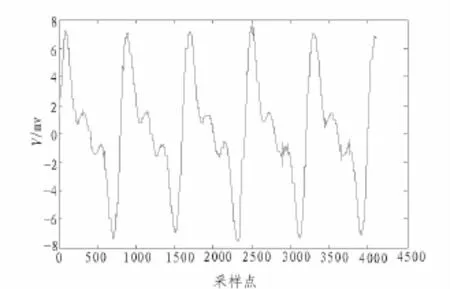
图3 平移不变量法去噪结果Fig.3 De-noising result of translation invariance method

3 小波变换模极大值滤波法

对检测的脉搏信号中混入的随机噪音，由于随机噪音的频谱很不规则，与有效信号的频谱差别不大，可以利用随机噪声的奇异性加以滤波。奇异性的大小用Lipshczti指数来度量。随机噪音的Lipshczti指数与有效信号本身的奇异点的Lipshczti指数大小不一样，从而它们的小波变换模的极大值在不同尺度下的传播行为也不一样[7]，随尺度变大而幅值减小的，认为是噪声产生的模极大值，予以去除；反之，则认为是由信号奇异点产生的，予以保留。对所有保留的模极大值进行重建，即得到去噪后的信号[8]。利用这一特征可将有效信号从随机噪音中提取出来。

具体算法如下：

1）根据信号的特征，确定小波基、分解层数，并对含噪声的信号进行小波分解；

2）在最大分解尺度 2 j上搜索极值点，并设定阈值去除小的模极值点，得到{wj}；

3）在 j层极大值点的位置，为2j-1尺度的极值点构造一个搜索领域，通常为 2 j尺度模极值点位置±3，±4个数据点；

4）根据搜索范围，把2j-1尺度极大值点落在该区域的点保留，其他的值置0；

5）令 j=j-1，重复操作，直到 j=2；

6）在j=2层存在极值点的位置查询j=1时相应极值点，其余位置将极值点置为0；

7）重构。

采用模极大值法去噪后的脉搏波信号如图4所示，从图中可以看出处理后的信号较为光滑。

图4 模极大值法去噪结果Fig.4 De-noising result of modulus maxima method

4 结 论

文中分别采用了3种小波去噪方法对脉搏波信号进行了去噪处理，采用小波变换阈值去噪法[9]去噪后，信号主要噪声得到抑制，且能反映原始信号的特征的尖峰点得到很好的保留。但是在信号的不连续点处，去噪后会出现伪吉布斯现象，且阈值的选择对去噪效果有着很重要的影响。为此，采用平移不变量法进行处理，处理后，伪吉布斯现象得到了很好的抑制。模极大值法能有效地保留信号地奇异点信息，去噪后的信号没有多余振荡，是原始信号的一个非常好的估计，但计算量很大，速度较慢。

[1]文莉，刘正士，葛运建.小波去噪的几种方法[J].合肥工业大学学报，2002， 25（2）:167-172.WEN Li，LIU Zheng-shi，GE Yun-jian.Several methods of wavelet denoising[J].Journal of Hefei University of Tecnology，2002，25（2）:167-172.

[2]胡昌华，李国华，刘涛，等.基于MATLAB的系统分析与设计—小波分析[M].2版.西安:西安电子科技大学出版社，2004.

[3]刘刚，屈梁生.自适应阈值的选择和小波消噪方法的研究[J].信号处理，2002，18（6）:509-512.LIU Gang，Q Liang-sheng.Study on wavelet adaptivethreshold denoising method[J].Signal Processing，2002，18（6）:509-512.

[4]王智，殷奎喜，赵华，等.基于小波变换实现脉搏信号降噪处理[J].通信技术，2011，5（44）:151-153.WANG Zhi，YIN Kui-Xi，ZHAO Hua，et al.Pulse signal noise reduction based on wavelet transform[J].Communication Technology，2011，5（44）:151-153.

[5]GUO Dai-fei，ZHU Wei-hong.A study of wavelet thresholding denoising[J].Signal Processing Preceding，2000（3）:29-33.

[6]Coifman R R，Donoho D L.Translation-invariant de-noisingwavelets and statistics[M].New York/Berlin:Springer Verlag，1995.

[7]Mallat S.Zero-processing of wavelet transform[J].IEEE Trans on Information Theory，1991，37（4）:1019-1033.

[8]陶维亮，王先培，刘艳，等.基于小波模极大值移位相关的光谱去噪方法[J].光谱学与光谱分析，2009，29（5）:1241-1245.TAO Wei-liang，WANG Xian-pei，LIU Yan，et al.A denoising algorithm forabsorption spectra by wavelettransform modulus maxima shift-related filter[J].Spectroscopy and Spectral Analysis，2009，29（5）:1241-1245.

[9]蒲会兰，丁世文，鲁怀伟，等.小波变换及其在信号去噪中的应用[J].现代电子技术，2012（19）:52-55.PU Hui-lan，DING Shi-wen，LU Huai-wei，et al.Wavelet transform and its application in signal denoising[J].Modern Electronics Technique，2012（19）:52-55.