系统辨识中最优采样间隔的确定

李立刚， 张召昕 ， 戴永寿， 张亚南， 昂 扬

（1.北京科技大学 自动化学院，北京 100083；2.中国石油大学（华东）信息与控制工程学院，山东 东营 257061）

在控制系统的分析和设计中，首先要建立系统的数学模型。控制系统的数学模型是定量描述系统或过程内部的物理量或变量之间关系的数学表达式[1]。对连续系统进行辨识时，输入、输出信号需要经过采样处理，采样间隔T的合理选择，关系到能否全面反映系统的动态特性以及辨识的精度。然而，在实际应用中，输入输出信号采样间隔的选取大多靠经验，国内外对这个问题的研究也比较少，因此，有必要对连续系统辨识中输入、输出信号采样间隔的选取方法作一定的研究。

1 采样间隔T的选择方法

采样间隔T的合理选择，原则上，要考虑以下几个方面的问题[2]：

1）频谱混叠问题：由Shannon采样定理知，若采样间隔T选得过大，即采样点离得太远，会引起低频分量与高频分量产生“混叠”现象，从而使辨识误差增大。此外，当T选得过大时，会导致采样信号中包含的被辨识系统的高频信息过少，无法准确反映系统的高频特性。

2）辨识的效率和工作量：若采样间隔T选得过小，即采样点离得太近，会导致差分方程近于线性相关，容易形成病态方程组。另外，当噪声干扰较大时，若T取得很小，还可能把噪声的特性反映到被辨识模型中。同时，若T取得过小，还会产生大量的多余数据，从而不必要地增加存储量和计算量。

3）信号的采样间隔T要与其他环节的时间间隔一致：例如，若辨识的目的是设计一个数字控制系统，则采样周期T须按照数字控制系统的性能及要求来选择。

现有的采样间隔选择方法主要有：根据被辨识系统的最高工作频率结合采样定理的选取方法，根据系统的时间常数以及过渡过程时间的选取方法等。它们都属于经验估计法，在精确程度上有所欠缺。

对于这个问题，加拿大学者SIMON S.UYKIN提出了关于采样间隔T的一种选取准则[3]：

式中λm为被辨识系统连续时间模型绝对值最大的特征值，T为被辨识系统输入输出信号的采样间隔。但是在实际应用中，待辨识系统的特征值的值通常是未知的，这样就在一定程度上限制了该准则的直接应用。

针对这个问题，N.K.Sinha教授提出了一种解决的方法[4]。该方法的基本思想为：对于在某个采样间隔T0下辨识得到的离散系统模型，首先计算它在z域中的特征值，并用双线性变换法[5]将其中模最小的特征值从z域变换到w域，然后根据w平面中该特征值到原点的距离d的大小判断采样间隔T0的合理性。根据式（1）给出的准则，Sinha在文献[4]经推导得，当d的值大约为5时，可认为相应的采样间隔T的取值是最优的。

这里使用双线性变换法将模型的特征值从z平面变换到w平面：

上式中，z=eα[cos β± jsin β]，相应的平面中的点由下式计算得到：

式中，

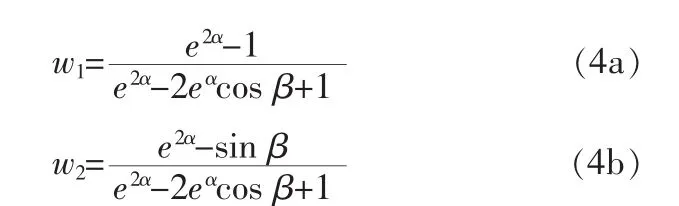
理论分析[4]表明，d的值随采样间隔T的增大而减小。本文利用d的值与采样间隔T的这种关系，结合折半查找法[6]的思想提出了一种寻找采样间隔最优值的方法。该方法首先设定采样间隔的初始选取范围，取中间值作为系统输入输出信号的采样间隔进行参数辨识，根据每一步计算中d值的大小不断地对采样间隔的取值范围“折半”，最终得到采样间隔的理论最优值。该方法的具体步骤如下：

Step0设置采样间隔取值范围的上限Tmax和下限Tmin，以及允许的误差限E；

Step1 若 Tmax－Tmin＜E，则跳转到 Step4，否则转到 Step2；

Step2 取采样间隔 T=（Tmax+Tmin）/2；

Step2.1以采样间隔T对原系统的输入输出信号进行采样，并用采样得到的输入和输出对系统离散模型的参数进行辨识；

Step2.2计算在当前的采样间隔下所得系统模型的特征值，使用双线性变换法将其最小的特征值转换到平面；

Step3计算平面中该特征值到原点的距离，记为d；

Step3.1如果d的值约为5，则跳转到Step4，否则转到Step 3.2；

Step3.2 若 d＜5，则令 Tmax=T，跳转到 Step1，否则转到Step3.3；

Step3.3令Tmax=T，跳转到 Step1；

Step4取当前的T为最优的采样间隔，结束。

其中，平面中极点到原点的距离d通过下式计算得出：

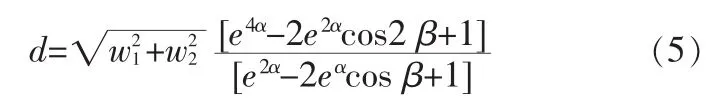
计算流程图如图1所示。

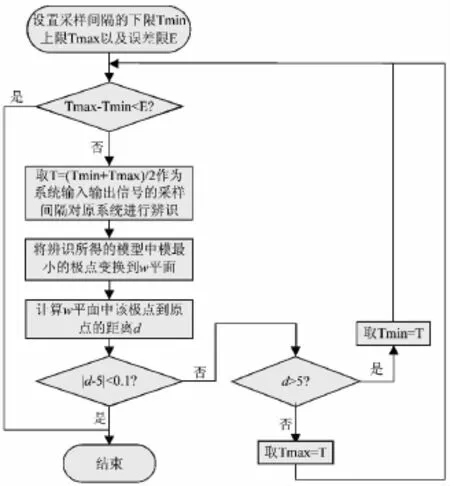
图1 采样间隔的选取步骤Fig.1 Method of sample interval selection

2 仿真实例

下面，文中通过一个实例对上述方法的应用作具体的介绍。

2.1 辨识对象

待辨识连续系统的传递函数模型为：

对上述系统施加如下的输入信号：

得到相应的输出为：

对式（7）和（8）表示的输入输出信号以 0.01 s的采样间隔进行采样，共采集300 s，得到30 000组输入输出信号的采样值。为了获得有色噪声，将随机数（近似的高斯零均值序列）通过如下形式的滑动平均滤波器:

将通过上述过程产生的噪声添加到输入输出信号的采样数据中，用添加噪声后的样本数据对原系统的离散时间模型在不同的采样间隔下进行辨识。在每10组采样值中取一组用于辨识即等价于采样间隔为0.1 s，每15组取一组即等价于采样间隔为0.15 s，以此类推。这样，在不同采样间隔情况下的数据时间长度是一致的，即皆为300 s，这样保证了不同采样间隔下辨识结果的对比分析的合理性。

这里采用如下形式的离散时间模型对系统进行辨识：

式中e（k）为白噪声，这里采用的参数辨识方法是递推增广最小二乘估计（RELS）法。

对于式（6）描述的连续时间系统模型可以通过阶跃响应不变法离散化为采样间隔T下的z域模型：

式中

其中，T 为采样间隔，a1、a2和 b0、b1即为采样间隔为 T时，所得离散模型的真实参数。

2.2 计算过程

Tmin可以取系统所允许的采样间隔最小值，这里取Tmin=0.01 s；Tmax可以取较大一点的值，这里取Tmax=2s。经过7步计算，d的值为4.95，已经非常接近5了，因此我们这里最终选取的采样间隔T为0.14 s。具体每步的递推计算结果如表1所示。

表1 递推计算过程Tab.1 Process of recursive calculation

式中θ与θ1分别为模型的真实参数向量与辨识所得的参数向量。

2.3 结果及分析

为了验证由该方法计算得到的采样间隔的是否为最优的，这里以 T1=0.01 s为初始值，T2=0.4 s为终止值，在[T1，T2]范围内每0.01 s取一个值作为对原系统进行辨识的采样间隔，在对应的采样间隔下分别对模型的参数进行估计并分别根据式（12）计算模型的参数辨识误差，在MATLAB下得到的仿真计算结果如图2所示。

表中Pe为模型的参数辨识误差，按（12）式计算

图2 不同采样间隔下参数辨识误差曲线Fig.2 Parameter identification error at different sample interval

将辨识中对原系统施加的信号分别输入到不同采样间隔下辨识得到的模型中，在MATLAB中计算得到模型的输出与原系统实际输出的均方误差曲线如图3所示。

图3 不同采样间隔下模型输出误差曲线Fig.3 Model output error at different sample interval

这里的输出误差是模型输出误差平方和的均值。

由此仿真结果可知，当采样间隔T取0.14 s时，辨识所得模型的参数辨识误差和输出误差均为最小，即T=0.14 s为对本例中的连续系统进行辨识的最优采样间隔。

从仿真结果可以看出，当采样间隔取值过小时，参数辨识误差及辨识所得模型的输出误差均较大。这是因为采样间隔T选得过小，采样点离得太近，导致参数辨识过程中的差分方程近于线性相关，形成了病态方程组所致。

当采样间隔的值大于最优采样间隔时，辨识所得模型的输出误差及参数辨识误差随着采样间隔的增大而增大，但是输出误差的增大相对并不十分明显。这意味着在实际应用中，可以在满足输出误差的前提下适当地增大采样间隔T，以减少计算量。

3 结束语

在连续系统模型辨识中，对于如何选取输入输出信号的采样间隔，目前的研究比较少，实际应用中大多也只是依靠经验。本文根据一种判断辨识中所用采样间隔的准确性的方法，提出了利用折半查的思想法寻找连续系统辨识中最优采样间隔的方法，与原有方法相比，该方法的使用不需要已知被辨识系统的特征值，具有一定的实际应用意义。

在该方法中，如何根据辨识对象的特性对初始Tmin与Tmax加以选择以减少计算的步数，以及如何将该方法从单输入单输出系统扩展到多输入多输出系统，还需要在以后的工作中继续研究。

[1]庞中华，崔红.系统辨识与自适应控制MATLAB仿真[M].北京:北京航空航天大学出版社，2009.

[2]王志贤.最优状态估计与系统辨识[M].西安:西北工业大学出版社，2004.

[3]SIMON S.UYKIN.A Unified treatment of recursive digital filtering[J].IEEE Transactions on Automatic Control，1972，2（17）:113-116.

[4]Prof.N.K.Sinha， B.Sc. （Eng.）， Ph.D.，e al.Choice of the sampling interval for the identification of continuous-time systems from samples of input/output data[J].IEE Proceedings，1985，6（132）:263-267.

[5]Ekman M，Larsson E K.Paramter estimation of continuoustime bilinear systems based on numerical integration and separable non-linear least-squares[J].Inernational Journal of Conrrol，2007，80（3）:329-339.

[6]Gupta，V..A Keyword Searching Algorithm For Search Engines[C]//Innovations in Information Technology，2007.Innovations ’07.4th International Conference on.18-20 Nov，2007:203-207.