非惯性系中的动力学问题探研

郑福昌

（武夷学院 电子工程系，福建 武夷山 354300）

非惯性系中的动力学问题探研

郑福昌

（武夷学院 电子工程系，福建 武夷山 354300）

在对惯性系与非惯性系之间的坐标、速度、加速度变换关系进行推导的基础上，对非惯性系中的动能定理、动量定理及角动量定理作一些探讨，并讨论了方程解的物理意义。

非惯性系；坐标变换；运动方程；三大定理

众所周知,以牛顿运动定律为基础的动力学方程，它只是在惯性系成立的。相对于惯性系作变速运动或转动的非惯性系,以牛顿运动定律为基础而推导出来的一些运动定理在非惯性系中不再成立。但在许多实际问题中,由于某种要求或出于方便经常要选取非惯性系。而在非惯性系中的动力学方程一般教材很少介绍。为了在非惯性系中处理一些力学问题,有必要研究在非惯性系中物体的动力学规律及所遵从的运动定理，故本文在对惯性系与非惯性系之间的坐标变换、速度之间的关系、加速度之间的关系系统介绍的基础上，对非惯性系中的动能定理、动量定理及角动量定理作一粗浅的探讨。

1 惯性系与非惯性系之间的坐标变换

设有一非惯性系O′-x′y′z′（以下简称k′系）相对于另一惯性系O-xyz（以下简称k系）作一般运动（既有平动由有转动），在k′系中其基矢分别为i赞′，j赞′，k赞′，在k系中其基矢分别为i赞，j赞，k赞，如图1所示。

图1 坐标变换

1.1 k系和k′系中质点矢径之间的关系在惯性系k中质点P的矢径

非惯性系k′中质点P的矢径表为

1.2 k系和k′系中质点速度之间的关系

在k系中质点的速度

在k′系中质点的速度

这时

v軆t称为牵连速度，它表示在k′系中r軆′处质点，由于k′系相对于k系的运动所牵连而得到的速度。其中v軆O′是参考点O′（k′系中坐标原点）的速度。表示相对于参考点O′为′的点的转动速度。

1.3 k系和k′系中质点加速度之间的关系

在k系中质点的速度

在k′系中质点的速度

据（2）式，加速度 a軆与 a軆r有如下关系：

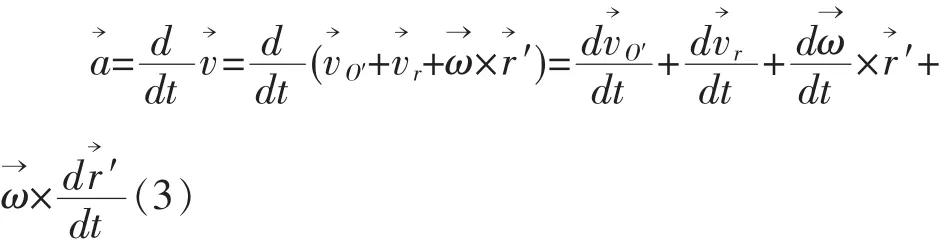
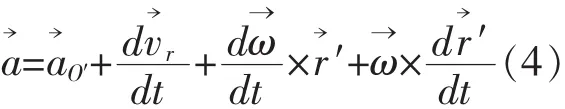
将（5）式代入（4）得

2非惯性系中的运动方程

在惯性系中质点的运动方程为

代入（8）式移项后得

为了在非惯性系中应用牛顿第二定律将（10）式表为

在（12）式中前两项分别是由于非惯性系平动和角速度的改变而产生的惯性力，而称为惯性离心力，（13）式中称为科里奥利力。

3非惯性系中质点运动定理的形式

3.1 非惯性系中质点的动能定理

（15）式表明：质点在非惯性系中动能的微分，等于作用与质点上的真实力于牵连惯性力在相对运动中的元功之和。

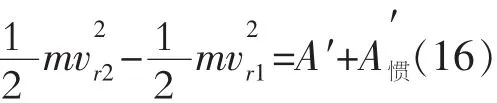
（16）式表明：质点在非惯性系中相对动能的该变量，等于作用与质点上的真实力于牵连惯性力在相对运动的路程上所作功之和。可以将这一结论称为非惯性系中的动能定理。

可以看出，在非惯性系下,由于科里奥利力F軋c始终不做功,因此,在非惯性系中应用相对运动的动能定理时不必考虑科里奥利力,即在非惯性系下质点动能定理比惯性系多了一项由于坐标系的牵连运动而产生的惯性力(牵连惯性力)对质点所做的功。

例1一光滑平面曲线细管，固定在水平面上。水平绕过定点O的铅垂轴以匀角速度ω转动。管P中有一小球，开始时小球相对于管的速度为零，小球与O点的距离为r0，如图2所示。试证当小球同O点距离为r>r0时，小球相对于管的速度为vr=

图2

解：以转动的圆盘为参考系(非惯性系)来研究这一问题。在水平面内作用在小球上的力有：管壁的约束力惯性离心力科里奥利力

当小球由r0运动到r位置时，外力的功

表示小球相对于非惯性系的元位移。

3.2 非惯性系中质点的动量定理

上式表明：作用于质点上真实力和惯性力的冲量等于质点在非惯性系中动量的增量。称为非惯性系中的动量定理。其中的大小由（12）式给出。一般运动情况下牵连惯性力与科里奥利力对非惯性系中的冲量均有贡献。

图3

解：地球既即有自转又有公转,所以是一个非惯性参照系,公转的角速度ω很小,可忽略含有ω2项的惯性力，并且可以认为地球绕地轴NS自转时,角速度ω軑=常矢量，即ω軑=0，a軆O=0，重力mg通过地球球心。由非惯性系中的动量定理的微分形式（14）式：

令转动坐标轴x、y、z与i、j、k重合，因ω与i、k共面，则：

于是：

将上式代入（4.4.1）式得质点P在三个坐标轴方向的运动微分方程为：

例3在水平光滑铁轨上有一小车,长为L,质量为M,车的一端站有一人,质量为m,人和车原来都静止不动(图4).现设人从车的一端走向另一端。如小车与人的摩擦系数为μ，问人和小车对地各移动了多少距离?

图4

解:取地为惯性系,车为非惯性系，取小车运动方向为中正向。选人为研究对象,并设人对车的速度为车对地的加速度为

由分析可知，在上式各项中，人在水平方向受到的真实力F=-μmg，与人运动方向相反。由于小车的加速运动人受到的惯性力为Ft=-maO′，与人运动方向相反。因平动柯氏力为零Fc=0。此时人相对非惯性系的初动量为零，末动量为-mv′。

以车为研究对象,地为参照系,在水平方向,应用牛顿第二定律有：

将aO′代人，并积分得

t是人到达小车另一端花的时间,所以小车相对地走的距离为：

人相对地走的距离为：

3.3 非惯性系中质点的角动量定理

（19）式可表为：角动量对时间的变化率等于外力、牵连惯性力、科里奥利力对O′点的力矩。称为非惯性参照系中质点对坐标原点的角动量定理。

图5

例4图5中,半径为R的固定圆盘放置在竖直面内,绳的一端绕在盘边缘上,另一端系一质量为的质点,竖直位置时AB=l,当m摆动时求其运动方程（绳质量不计）。

解：将动系的原点选在绳和轮的接触点上，即o-xyx系为一平动的非惯性系则质点m对原点o的角动量为

通过上述例题验证说明，本文所导出的在非惯性系中的动能定理、动量定理、角动量定理，不仅在形式上与我们所熟知的惯性系中动能定理、动量定理、角动量定理具有相似性，同时在非惯性系中应用时也同样能得到正确的结论。从而为我们在非惯性系中处理一些物理问题提供了一种方法。

O313

A

1009-9530（2013）04-0099-05

2013-06-07

郑福昌(1960-)，男，武夷学院电子工程系副教授，从事理论物理教学及研究。