考虑在线公交优先需求的离线信号周期优化模型

马万经,叶新晨

(同济大学道路与交通工程教育部重点实验室,上海200092)

考虑在线公交优先需求的离线信号周期优化模型

马万经*,叶新晨

(同济大学道路与交通工程教育部重点实验室,上海200092)

信号周期是交通控制的主要参数之一,也是影响交叉口公交车辆延误的主要因素.本文提出考虑在线优先需求的离线信号周期优化结构模型,其最优周期由离线基本周期和在线增量两部分构成.离线基本模型以加权车均延误为目标,探讨公交权重的影响因素及其与公交运行效益、社会车流运行效益的关系;在线增量计算以在线优先策略提供可实施空间为目标.分析一个四相位信号控制交叉口,对所提模型进行仿真验证.结果表明,公交车均延误最小的最优周期和社会车流车均延误最小的最优周期并不重叠,在一定的公交权重下,模型能够求得二者加权最优解.适当的在线增量引入,能够进一步降低公交车辆延误,且不会对非优先车流产生较大影响.

城市交通;信号周期;交通仿真;公交信号优先;延误

1 引 言

公交优先在改善公交服务,提高公交系统吸引力方面有非常大的潜力.TCRP的研究报告将公交优先分为主动优先、被动优先和实时优先三大类[1].在考虑公交优先后,最佳信号周期的确定是被动优先研究的主要内容之一.相关研究认为,小周期利于公交优先,主要是由长时间的统计分析上看,小周期下公交车辆的延误要小于大周期下的延误[2-4].同时,由于公交车辆与社会车辆的一个显著区别是公交载客量远大于社会车辆,进而公交车辆的运输客流效率远大于社会车辆.因此,信号控制下,相同的车均延误,对公交车和社会车辆造成的影响不同.基于这一基本考虑,相关研究提出了在以人均延误为目标进行公交优先条件下,信号控制参数的优化[5-7].而Peter等人研究指出,人均延误目标优化可能会夸大公交优先的效果,并造成社会车流运行效益的降低[8].

本文提出了考虑离线与在线需求的信号周期优化模型.离线模型以加权车均延误为目标,进行公交优先条件下信号周期的优化求解;研究中深入探讨公交权重的影响因素及其与公交运行效益和社会车流运行效益的关系.在线增量的计算目标是为在线优先策略提供可实施空间.以一个四相位信号控制交叉口为分析对象,对所提模型进行仿真验证,并分析了相应结果产生的原因.研究表明,公交车均延误最小的最优周期和社会车流车均延误最小的最优周期并不重叠,在一定的公交权重下,模型能够求得二者加权最优解.权重的取值将直接影响最优周期的优化结果,影响的大小取决于公交流量比和社会车流量比之间的相对关系.在线增量是公交流量、社会车流量、离线基本周期和在线优先策略的函数,适当的在线增量引入,能够进一步降低公交车辆的延误,但不会对非优先车流产生较大影响.

2 问题描述

Webster提出了信号控制交叉口延误计算公式和最优周期计算公式

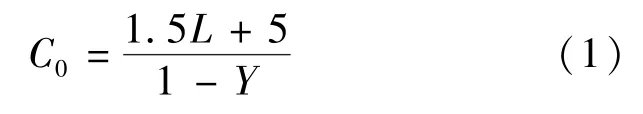
式中 C0为最优信号周期时长,s;L为信号周期总损失时间长度,s;Y为关键流量比之和.

由于公交车辆延误与社会车流延误不能直接比较,因而式(1)在考虑公交后不能直接应用.在流量比较大(即关键流量比之和接近于1)时,用式(1)计算出的最优周期值趋向于无穷大.同时,信号周期的确定还必须考虑在线实时优先的可行性,为其预留足够的实施空间,即考虑公交优先的信号周期应由离线最优周期和在线增量两部分构成.为简化问题,假设交叉口设有公交专用道.对于没有公交专用道的情形,则需要考虑公交与小汽车之间的相互影响后才适用本模型.

3 离线基本周期优化模型

将离线最优周期的求解归纳为一个以加权平均延误最小为目标,以相位最大、最小绿灯时间和最大、最小信号周期为约束条件的数学规划问题.在给定的信号周期下,绿信比按照等饱和原则进行分配.延误的计算采用HCM2000的延误模型,避免Webster延误模型在饱和度较大时延误也趋向于无穷大的缺点.

3.1 目标函数与约束条件

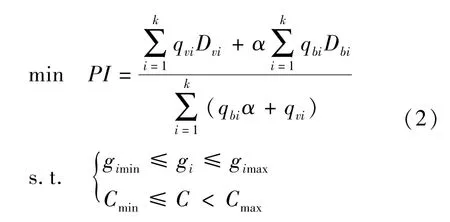
式中 Dvi为社会车流i车均延误,s/veh;Dbi为公交车流i车均延误,s/veh;qvi为社会车流i流量,veh/h; qbi为公交车流i流量,veh/h;α为公交车均延误权重(相对社会车均延误权重1);C为信号周期,s;Cmin, Cmax分别为最小和最大周期长度,s;gi为车流i的绿灯时间;gimin、gimax分别为最大最小绿灯时间.

3.2 绿信比分配模型

信号周期与绿信比是相互耦合的一对信号控制参数,本文在进行信号周期优化的过程中,绿信比按照等饱和分配.即在信号周期C下,相位i的绿灯时间可以用式(3)计算

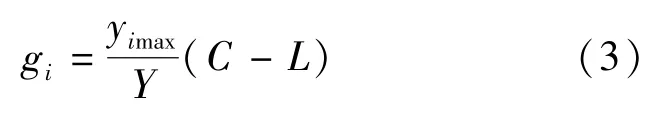
式中 yimax为相位i中的关键车流量比.在有公交专用道的情况下,公交车流的流量比单独计算,此时yimax为i相位公交流量比和社会车流量比中的较大者.

3.3 延误计算模型

为了克服基于Webster延误公式优化方法的缺点.使用HCM2000的车均延误公式作为目标函数

式中 d为车均延误,s/veh;d1为均衡延误, s/veh;g为绿灯时间长度,s;PF为均衡延误协调系数(PF=1,单个交叉口);d2为包括随机延误和过饱和延误在内的额外延误;d3为初始排队延误(假设初始排队为0);T为分析时段,h,T=0.25 h; K为额外延误系数(取决于控制类型);I为上游协调调整系数;x为车道组饱和度.

3.4 模型求解流程

式(2)为一整数规划模型,用枚举法求其最优解,求解流程如图1所示.在周期取值范围内,从最小周期开始,以步长m(通常取1 s)进行搜索,比较并记录PI值最小所对应的周期.遍历所有的周期值之后,所求的周期Copt即是最佳周期.

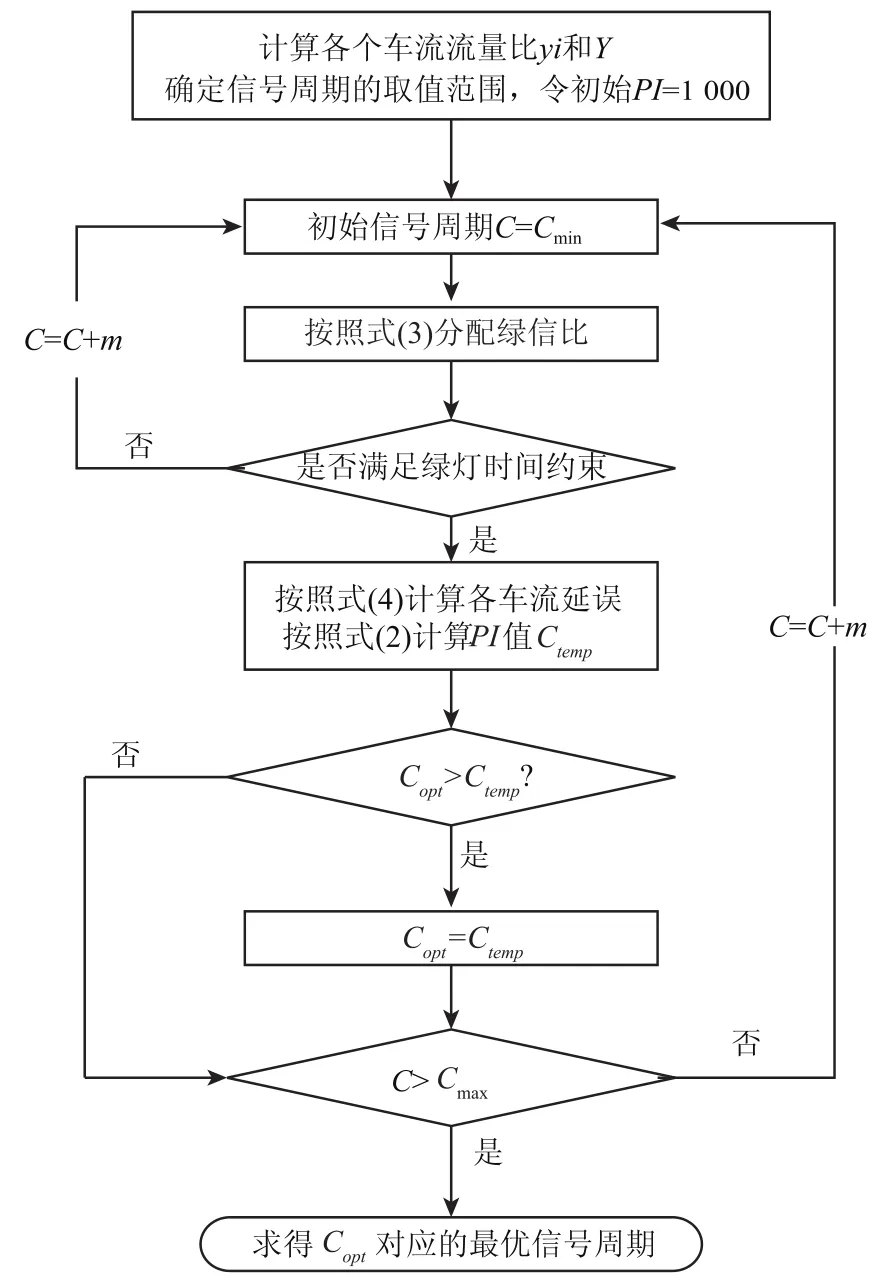
图1 离线最优周期求解流程Fig.1 Algorithm for optimal offline cycle length

4 算例分析

4.1 离线模型分析

采用济南市无影山路交叉口为案例进行分析,交叉口的交通设计、流量及交叉口相位设计如图2所示.一条公交专用道为东西方向(在相位P1中通行),位于道路中央.其中,公交车流量的取值从50 veh/h变化到250 veh/h,取权重w从1变化到91,详细的取值情况如图3、图4所示.算例主要分析不同公交流量下(即不同社会车流与公交车流量对比情形下)和不同权重下模型最优解的变化情况.一辆双铰接公交车按载客人数160人计算,其载客量可能是小汽车载客量(按照每车2人计算)的80倍.按人均延误优化的结果,权重的波动范围取为1～91.应是权重的波动范围对应公交流量和权重下,效益指标的变化趋势,如图3、图4所示.

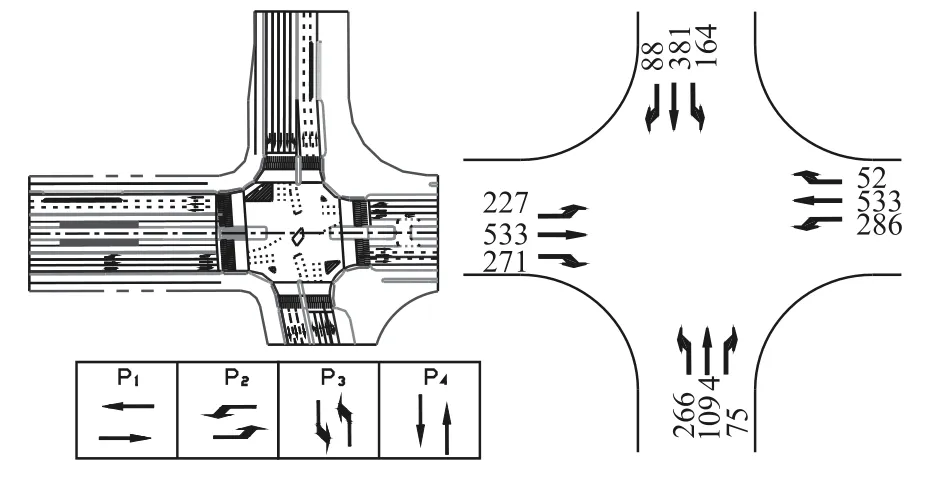
图2 无影山路—北园大街交叉口示意图Fig.2 Wuyingshan—Beiyuan intersection

图3 最优周期随权重变化趋势(qb=150 veh/h)Fig.3 Impacts on optimal cycle length(qb=150 veh/h)

从图3和图4中可以看出,当公交流量较小时,最优周期随权重的大幅度变化并不敏感;当公交流量较大时,最优周期随权重的大幅增加反应相对敏感.产生这一现象的主要原因在于公交最优周期与社会车流最优周期的相对位置,以及其之间的差距在不同流量对比条件下发生了显著的变化.值得注意的是,在公交流量较大时,过大的权重可能造成模型的解落在边界位置.与此同时,还可以发现在公交流量较小或较大的情况下,当公交权重取值较大时,模型最优解相对于社会车流的最优周期而言会发生较大的变化,随之社会车流的延误大幅增加,而公交车流延误的降低幅度则十分有限,如图5和6所示.

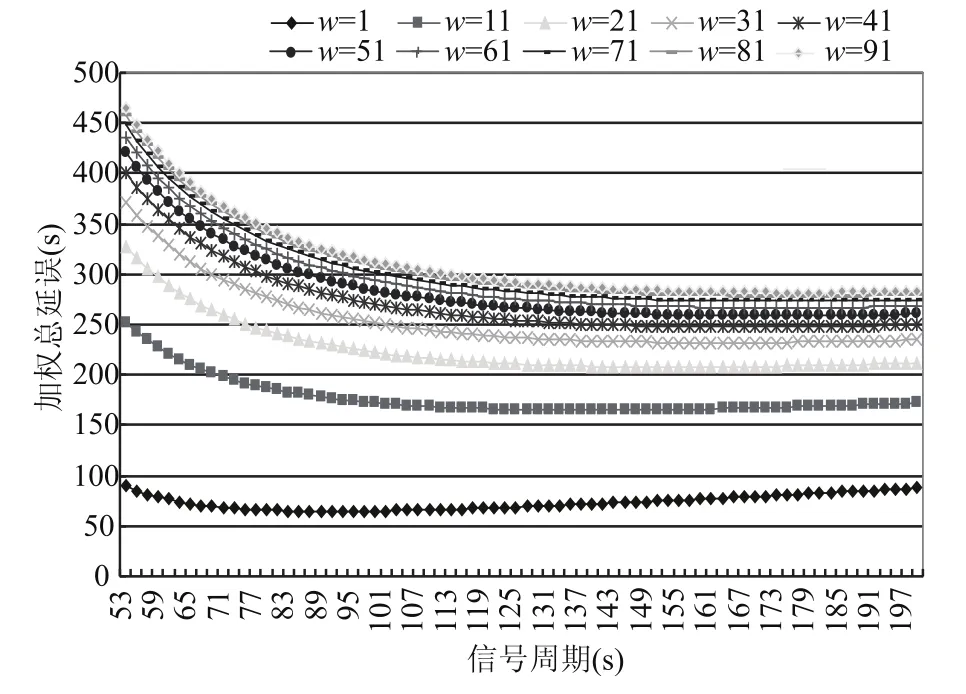
图4 最优周期随权重变化(qb=250 veh/h)Fig.4 Impacts on optimal cycle length (qb=250 veh/h)

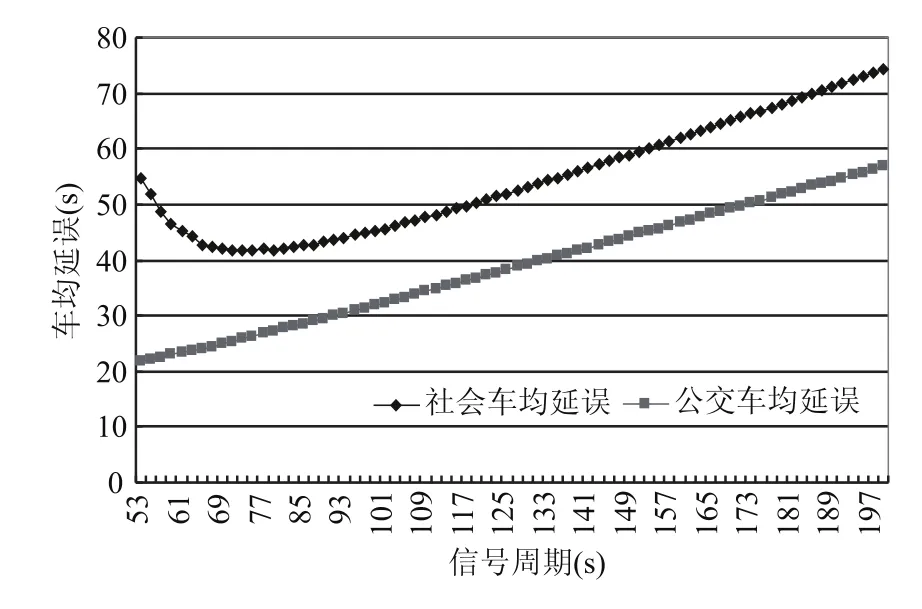
图5 最优周期的对比关系(qb=50 veh/h)Fig.5 Compare of optimal cycle length(qb=50 veh/h)

图5中,公交最优周期远小于社会车流最优周期,随着权重的增加,加权最优周期将逐渐接近于公交最优周期,这一过程对社会车流而言,信号周期的变化范围恰恰是延误对周期最敏感的区域,从图中可以看出相同的周期变化量下,社会车流延误增加的幅度接近于公交车流延误降低幅度的2倍.从斜率来看,相差没有这么大.

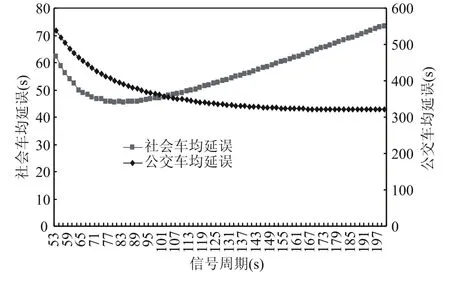
图6 最优周期的对比关系(qb=150 veh/h)Fig.6 Compare of optimal cycle length(qb=150 veh/h)

图6中,公交最优周期远大于社会车流最优周期,在加权最优周期随着权重的增加逐渐靠近公交最优周期的过程中,社会车流的延误增加速度要远大于公交车流延误降低的速度.

因此,当公交车流最优周期与社会车流最优周期位置的相对距离较大时,权重的取值需要根据社会车流所能承受的服务水平降低的程度来决定.各自的最优周期可用本文模型求解,即求公交最优周期时,取小汽车权重为0;求小汽车最优周期时,取公交车权重为0.过大的权重,如以载客量为权重(双铰接公交车),即以人均延误最小为目标求解,则会造成最优周期取值显著偏离社会车流本身的最优周期,将引起社会车流的拥挤,这种拥挤反过来也会影响公交信号优先策略的实现.

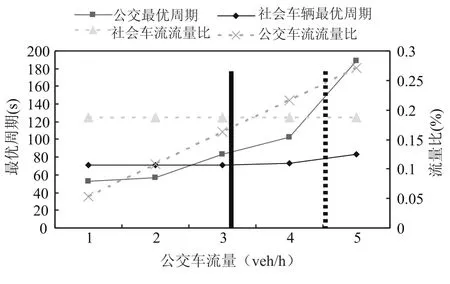
图7 不同目标下最优周期随公交流量变化趋势Fig.7 Impacts of different objectives on optimal cycle

图7表述了不同的公交流量,也即不同的公交流量与社会车流量对比(图中所列社会流量比是指与公交同一相位的社会车流量比)的条件下,不同目标下的最优周期变化趋势.为突出对比关系,在图中列出了不满足相位最小绿灯的信号周期.公交延误最小为目标的最优周期随公交流量的增加而增加.这一单调关系的出现是由于当公交流量较小时,在绿信比等饱和分配的过程中,公交专用道的流量比不作为分配依据.在公交流量到达一定程度后,以社会车流延误最小为目标的最优周期都随公交流量的增加而有一定程度的增加.其原因在于公交流量增加到一定程度之后,公交专用道流量比超过同相位社会车流量比,被作为该相位绿信比分配依据.

从图7中还可以明显看出“小周期有利于公交优先”这一结论的局限性.当公交流量较小,即图7中公交流量处于黑实线以左的区域时,公交流量比小于社会车流量比,同时公交车流最优周期小于社会车流最优周期,此时,在社会车流最优周期的基础上降低周期值有利于降低公交车辆延误;当公交流量较大,即图中公交流量处于黑虚线以右的区域时,公交流量比大于社会车流量比,同时公交车流最优周期大于社会车流最优周期,此时,在社会车流最优周期的基础上降低信号周期反而会增加公交车流的延误;当公交流量比落于黑实线与黑虚线之间时,公交流量比小于社会车流量比,而公交车流最优周期大于社会车流最优周期.

4.2 在线增量仿真分析

在线增量的研究通过 VISSIM软件提供的VISVAP编程工具实现.感应控制逻辑为在固定周期和最大最小绿灯约束下,根据公交优先的申请来进行感应控制.取公交车流的权重为1,根据式(2),采用枚举算法(流程如图1)求得最优周期的值为54 s.在实验中,信号周期从54 s开始,在线增量以5 s为步距,增加信号周期至79 s.以54 s时的延误为基准,公交车均延误、优先相位社会车流延误、非优先相位社会车流延误随在线增量增长而增加的比例如图8所示.

从图8中可以看出,引入在线增量之后,非优先相位机动车流延误上升,公交车辆延误和优先相位机动车流的延误呈现下降趋势.且随着信号周期逐渐增大,非优先相位延误增加的速度也增加,而公交相位和优先相位延误降低的速度逐渐减少.当在线增量增加到一定程度之后,公交相位和优先相位的延误不降反增(降低幅度回落).

由此可见,适当在线增量的引入能够进一步降低公交车辆延误.而当在线增量超过一定幅度之后,由于周期长度增加引起的延误增加幅度,超过了由周期增加引起的优先策略实施空间和由灵活度增加而产生的公交车流及优先相位社会车流的延误减少幅度,从而造成公交车辆和社会车辆的延误不降反升.也就是说,在线增量对优先相位车流(公交车流和社会车流)的延误有双重作用.

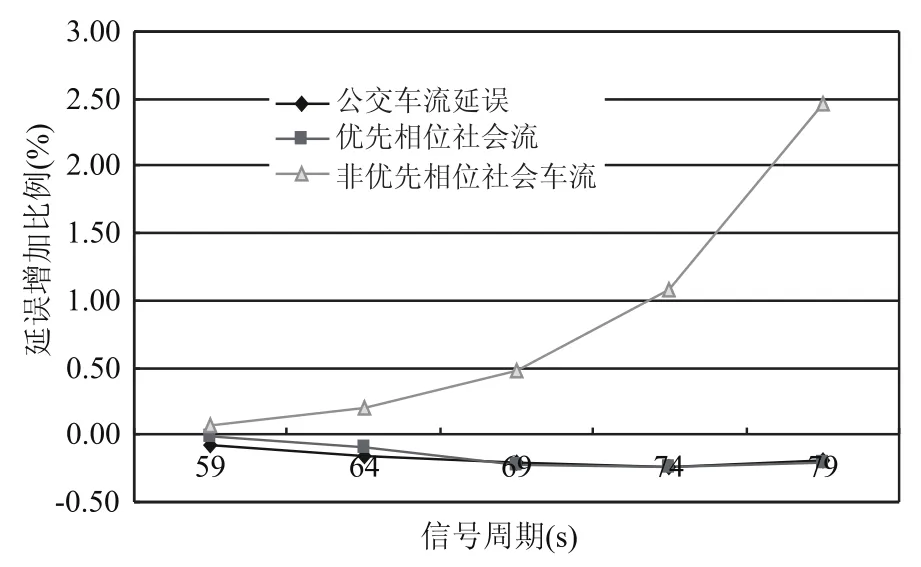
图8 离线信号周期在线优化的适应性分析Fig.8 Adaptability analysis of offline optimal cycle

同时,对于交叉口的总体效益来所,不同权重下的加权平均延误随周期增加的变化趋势如图9所示.显然,随着公交权重的增加,加权延误随信号周期增加而增加的速度逐渐降低.在本研究中,当权重增加到10时,加权平均延误—信号周期关系曲线出现拐点.这就意味着存在一个最优周期,使得公交车流和社会车流的加权延误最小,且这一周期值等于离线最优周期与在线增量之和.

图9 不同权重下加权平均延误变化趋势Fig.9 Impacts of weight on delay

对于交叉口的总体效益,在线增量的效果与两个主要因素相关:其一,在线增量本身对优先相位车流(公交车流和社会车流)的双重作用及其相对关系;其二,公交车流的权重,权重越大,在线增量的效益越明显.显然,在线增量的取值与公交车流量、社会车流量、基本周期时长、公交的权重和可能采取的公交优先策略相关.

5 研究结论

公交信号优先是降低公交延误,提高公交系统可靠性的重要手段.合理的信号周期长度对信号优先效益的充分发挥有重要意义.本文研究了信号优先条件下信号周期最佳计算方法,主要结论如下.

(1)最优周期应包括离线优化基本周期和在线增量两部分,以此来实现离线和在线的组合最优.加权最优信号周期能够取得公交车流和社会车流效益的均衡;公交车流最优周期和社会车流最优周期的相对位置决定了加权最优周期对各自效益的影响.

(2)不同条件下,权重的变化对公交车流和社会车流延误的影响程度和速度不同.而总的来说,在小周期条件下,加权的效果十分明显,对权重的取值也比较敏感.

(3)小周期并不一定利于公交优先,需要根据公交车流延误随周期值的变化规律进行判断;在离线最优周期的基础上增加合适的在线增量,可以降低公交车辆延误且对社会车流影响不大.而在线增量的效益取决于所提出的两个因素.

研究仅仅是对离线公交优先与在线公交优先集成优化的初步探讨,后续的研究应该针对不同的交通条件和道路条件,对本文方法实用性进行验证和分析,并给出具体的权重取值建议.

[1]Skabardonis A.Control strategies for transit priority[J]. Transportation Research Record,2000(1727):20-26.

[2]Vasudevan M.Robust optimization model for bus priority under arterial progression[D].Maryland:University of Maryland,2005.

[3]Ma W,Yang X,Liu Y.Development and evaluation of a coordinated and conditionalbus signalpriority approach[J].Transportation Research Record,2010 (2145):49-58.

[4]Ngan V,Sayed T,Abdelfatah A.Impacts of various traffic parameters on transit signal priority effectiveness [J],Journal of Public Transportation,2004,7(3): 71-93.

[5]Yagar S,Han B.A procedure for real-time signal control that considers transit interference[J],Transportation Research,1994,28B(4):315-331.

[6]Kim W,Rilett L R.Improved transit signal priority system for networks with nearside bus stops[J]. Transportation Research Record, 2005(1925): 205-214.

[7]Stevanovic J,Stevanovic A,Martin P T,et al.Stochastic optimization of traffic control and transit priority settings in VISSIM[J].Transportation Research C,2008,16 (3):332-349.

[8]Furth P G,Cesme B,Rima T.Signal priority near majorbus terminal[J]. Transportation Research Record:Journal of the Transportation Research Board, 2010,12(1):89-96.

Optimal Offline Cycle Length Model Based on Online Bus Priority Demand

MA Wan-jing,YE Xin-chen
(Key Laboratory of Road and Traffic Engineering of the Ministry of Education,Tongji University,Shanghai 200092,China)

Cycle is one of the most important parameters of traffic control system which has many effects on the delay of buses.The basic requirement of bus signal priority is to decrease bus delay at intersections. First,the optimal cycle length model under the condition of bus signal priority is developed by giving different weight to vehicles and buses.Then,a four-phase signal controlled intersection which has an exclusive bus lane is adopted to validate the optimal cycle length model and analyze the effects of different weight.The results show that the optimal cycle for buses and vehicles is not equal.And the weighted optimal cycle length model can make a trade-off between buses and vehicles.Finally,the appropriate on-line increment of cycle can further reduce the delay of buses and would not affect the non-priority vehicles.

urban traffic;cycle length;traffic simulation;transit signal priority;delay

U491.51

A

U491.51

A

1009-6744(2013)01-0124-06

2012-08-13

2012-09-13录用日期:2012-09-19

国家863计划课题(2011AA110305).

马万经(1980-),男,内蒙古赤峰人,副教授.

*通讯作者:mawanjing@gmail.com