基于VISUM模型的公交OD反推研究——以西宁市为例

蔡 军,刘 锴,刘涟涟

(大连理工大学a.建筑艺术学院;b.交通运输学院,辽宁大连116024)

基于VISUM模型的公交OD反推研究
——以西宁市为例

蔡 军*a,刘 锴b,刘涟涟a

(大连理工大学a.建筑艺术学院;b.交通运输学院,辽宁大连116024)

OD矩阵是公交线网规划和线网优化的重要依据.OD矩阵反推是获取公交OD数据的有效方法.相关文献中,针对城市整体公交体系的研究较少.依据西宁市建成区所有公交线路上客、下客、车上乘客的调查数据,采用VISUM软件构建了基于等概率下客分布、距离概率下客分布的公交OD矩阵反推模型;然后在VISUM全市整体公交模型中,将各线路反推所得到的OD矩阵归并至交通小区,并通过模型分配得到的路段客流与线路调查得到的路段实际客流比较,检验公交OD反推方法的有效性.研究表明,等概率分布OD矩阵反推在西宁案例中的精度与可靠性较高.最后指出,乘客在各站的下客概率影响因素较多,把握并合理运用其规律是公交OD反推的关键.

城市交通;OD反推;VISUM;公交;上下客

1 引 言

公交线网优化、公交专项规划是促进公交健康发展的有效保障,并需要公交客流量、出行时间分布、上下客分布、OD分布等调查数据的支撑.公交OD矩阵描述了公交客流在网络中各个OD点对间的分布,是公交线网规划和线网优化的重要依据,是公交客流分配和预测的基础.然而,公交OD调查费时费力,难度和成本较大,因此OD反推和预测一直是线网规划研究的热点[1].

公交OD反推技术起源于机动车OD反推.目前常用的OD矩阵推算模型有广义最小二乘法、最大似然法、最小信息量法、极大熵法和人工神经网络等方法.OD反推算法与各站点的下车概率有关;武荣桢等对基于公交站点上下客人数反推OD矩阵的概率论模型进行了研究[2].公交OD反推还包括上下客及客流获取方式层面的研究.上下客及客流获取包括跟车调查法、GPS定位与乘客IC卡刷卡信息法、手机定位法等.其中跟车调查是常用的数据获取方法;GPS定位及IC卡刷卡在调查期间的人工投入方面有所节省;手机定位法已有研究,但应用较少.

周雪梅等[3]通过公交IC卡信息获得的数据研究了公交出行特征,以公交站点上下客人数为约束条件,提出了综合考虑公交乘客上下车概率与公交站点产生吸引因素的反推模型;邹亮等[4]提出利用移动定位技术获取公交OD方法的思路,阐述了基于手机定位技术的公交OD数据的获取方法及其步骤.然而,我国不少城市公交IC卡普及率偏低;手机定位法技术不成熟以及个人隐私和与相关技术、管理部门交涉的问题.因此,二者存在一定的局限性.此外,在目前的研究中,结合小区域或较少线路的案例研究较多,以特大城市整体公交线网为例的研究较少.

西宁作为公交出行率较高的大城市,其公交IC刷卡乘客基本在50%左右,且没有公交GPS定位系统.西宁目前的公交IC刷卡数据只记录乘客上车站点,不记录下车站点.在该情况下,对西宁IC卡数据的简单汇总分析,可以得到不同线路在各时段客流量的大小,但只限于线路客流的总体情况,不能提供准确的各站点各断面的客流变化和各站下客情况.针对西宁现状,依然需要采用传统的随车调查法获取上下客及客流信息.VISUM作为一款用于宏观模型的软件,自身并没有提供公交OD反推模块.研究针对西宁城区每条公交线路的每个方向,采用VISUM软件构建相应的OD反推模型;然后在全市的公交模型中,将各线路反推得到OD矩阵归并至交通小区,并通过模型分配得到的路段客流与线路调查得到的路段实际客流比较,检验公交OD反推方法的有效性.

2 公交OD反推模型的构建原理与方法

2.1 VISUM中的OD反推模型构建

一条线路包括若干个站点,可将站点视为交通小区,可将线路视为路径.将某站的上客人数作为交通小区的发生量,各站的下客人数作为交通小区的吸引量.模型考虑线路方向,即某站上车的乘客只能在前进方向的站点下车.可以假定或调查分析获得某一站上车的乘客在后续各站的下车概率.进而依据上车乘客、下车乘客、各站吸引概率,通过双约束、重力模型法推算各站OD.

PTV公司的VISUM11.0软件自身不带有公交OD反推模块,需要根据反推原理构建公交OD反推模型.构建方法如下:

(1)以站点顺序建立交通小区,如站点1用交通小区1替代;构建了包括54个站点的标准分析模型;通常站距约0.5 km,标准模型的容许线路长度在27 km以上.

(2)在交通小区属性中添加上客、下客、距下站的距离、站点名称、各站车上乘客人数等属性.

(3)通过属性计算将站点距离属性、车上调查乘客属性等赋值给路段属性.

(4)通过属性计算将无过客流量、上下客人数的站点,以及对侧反向路线站点之间的路段长度赋予无穷大的距离,从而达到OD分布只沿前进方向进行的目的.

(5)采用重力模型约束各站的上客发生量、下客吸引量(见式(1)～式(3)),然后通过公交分配得到各站的上下客、过客流量、线路OD等相关数据.

模型所采用的计算公式如下:

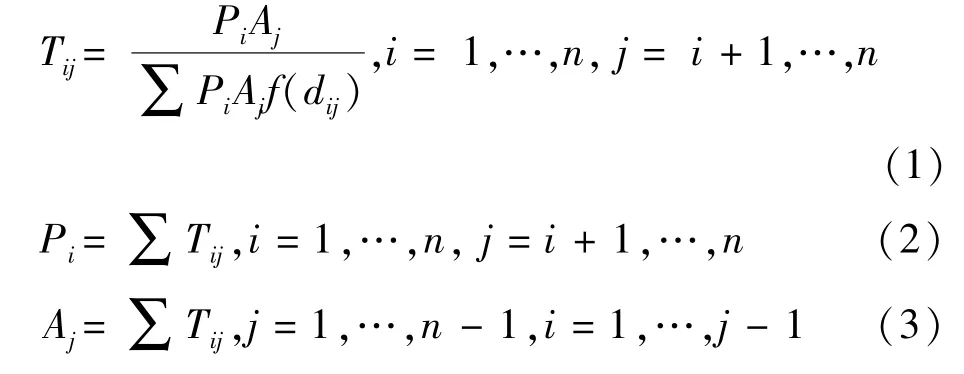
式中 Tij——i站到j站的公交下车人数;

Pi——i站总上车人数;

Aj——j站总上车人数;

dij——i站到j站的乘距;

n——线路总站数;

f(dij)——站点i到站点j的下客人数与dij的函数.

2.2 后续站点下客概率分布分析

传统的公交OD矩阵推算方法的假设是:当公交车辆到达j站时,j站前上车的每一位乘客都以相同的概率在j站下车,而不论他在前方哪一站上车.因此对于式(1),设f(dij)=c,c为大于零的常数.如不考虑距离因素影响,在以后第1站下客的概率、第n站下客的概率只与第1站、第n站的下车统计人数相关,本研究将这种方法称为“等概率反推”.

窦慧丽等认为居民公交出行的距离分布有一定规律,传统的公交线路客流OD分布推算方法精度不高;认为公交乘客出行站数近似服从泊松分布[5],基于公交乘客下车概率,以公交站点上下客人数和路段客流量为约束条件,提出了单条公交线路客流OD矩阵的推算方法,但其反推OD的下客站客流量误差相对偏大.刘翠等[6]建立了根据公交乘客上下车人数推算公交线路客流OD矩阵的极大熵模型,其模型亦考虑了站数对乘客下车概率的影响.由公交出行特点可知,公交出行属于中长距离出行,出行时间过长或过短的居民则很少采用公交这种出行方式[7].基于上述研究,对于式(1),可设f(dij)为随乘距而变化的函数.将这种方法称为“距离概率反推”.

3 西宁公交调查数据

3.1 公交调查概况

大连理工大学西宁项目组经过为期10天的精心准备,在公交公司的大力配合下,聘请青海民族学院200名学生,10名教师,分3日进行随车客流调查,车辆计划抽样率为33%.要求学生记录每站的上下乘客、时间.总计调取了全市64条线路全天的公交上下客数据.通过与公交公司的客流总量比较,调查数据可信.

3.2 公交调查数据

单条线路的OD反推以1路生物园区至建国南路(简称1路下行)的调查数据为例.图1为1路下行的日客流分布,图2为1路下行的乘客上下客分布.

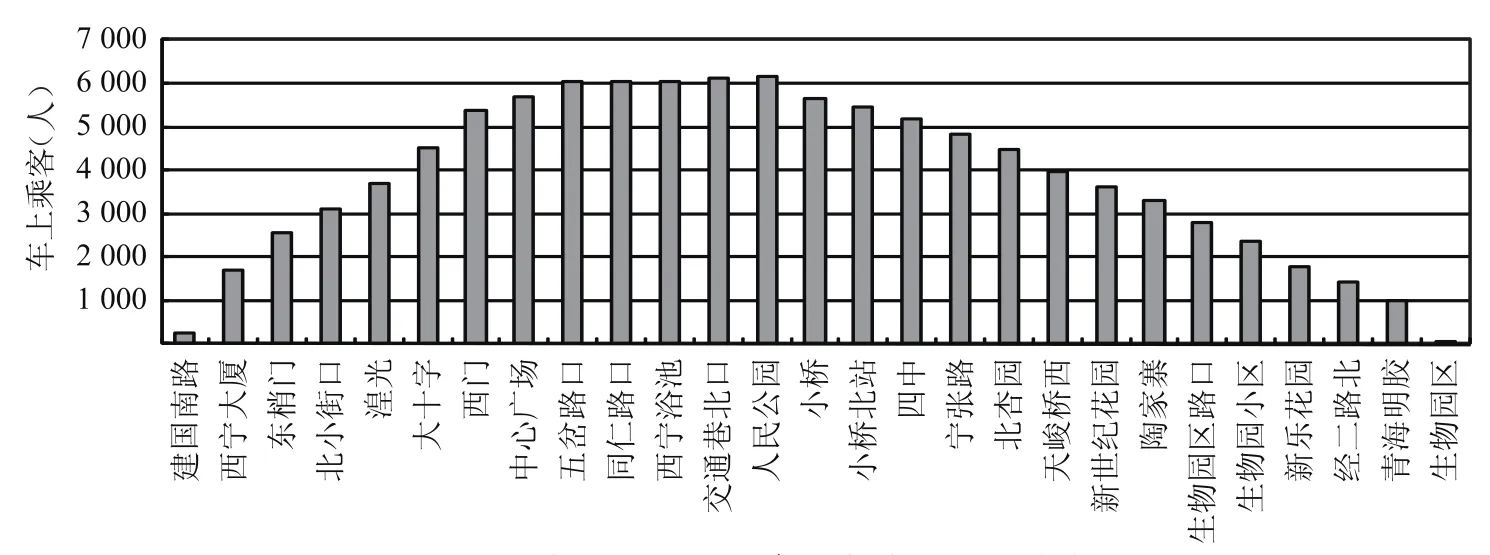
图1 1路生物园区至建国南路日客流分布Fig.1 Passenger flow of a day of bus line 1 from Biotech Park to Jianguo South Road

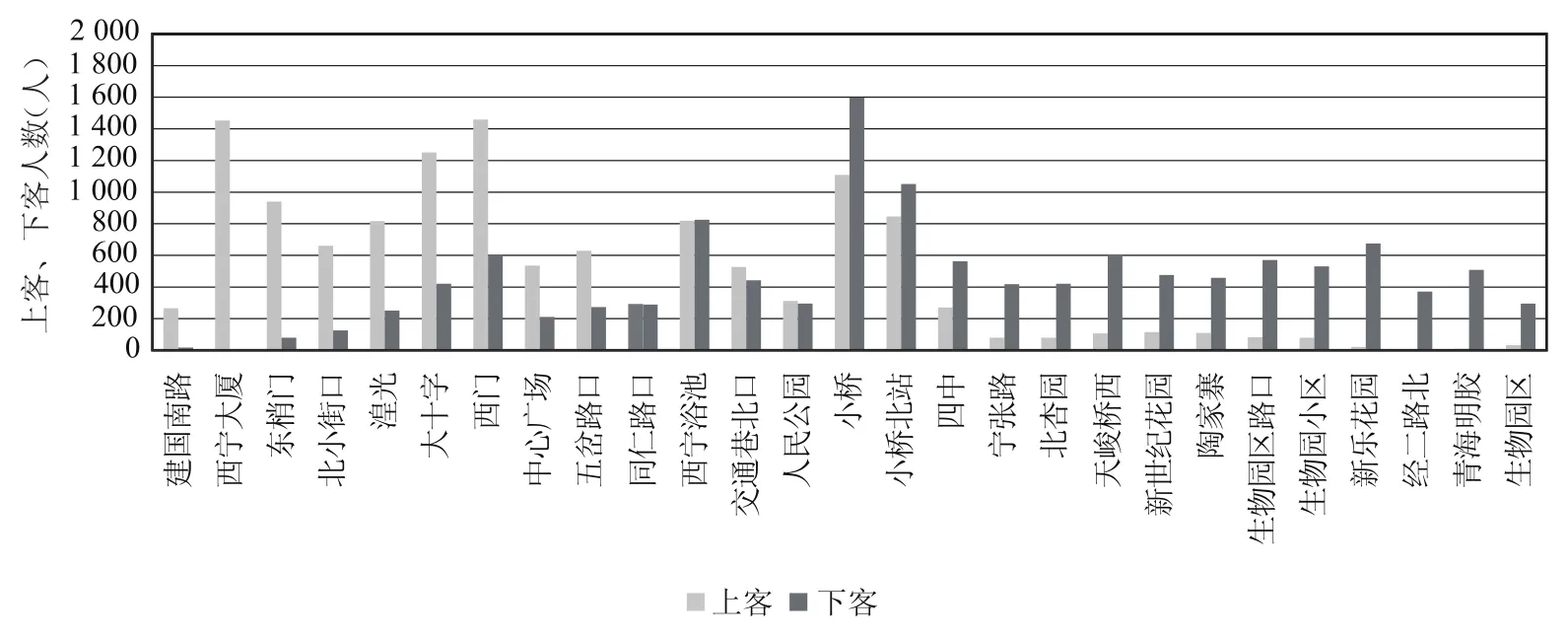
图2 1路生物园区至建国南路上下客分布Fig.2 Boarding and alighting Passenger a day of bus line 1 from Biotech Park to Jianguo South Road

3.3 居民出行调查数据

西宁居民出行调查自2011年4月17日至5月12日,历时近1个月.调查得到市教育局的支持.规划组向中小学生发放3 000套调查表,其中包括学生家庭表、邻居家庭表各1 500套.经筛查并补充内容(如核实出行距离、补充出行距离).具有出行时间、确切出行距离、明确目的地的非学生有效出行2 955次、学生1 037次,合计调查出行次数3 992次.

根据居民出行调查,西宁全日平均单程出行距离4.04 km,各交通方式中公交4.86 km,小汽车6.26 km,步行1.57 km.根据公交随车调查数据,可采用站点-线路录入法获取各线路的公交上下客、过客分布,进而得到调查日所完成客运周转量与客运量.经测算,全市日客运周转量为494.34万人公里,客运量为122.6万人次,日平均乘距为4.03 km,早高峰为4.31 km.计入两端步行距离(根据出行调查,平均到站距离约0.3 km,两端按0.6 km计算),公交平均出行距离为4.63km,与居民出行调查数据吻合.扣除两端步行距离可得到图3所示的公交出行乘距分布.

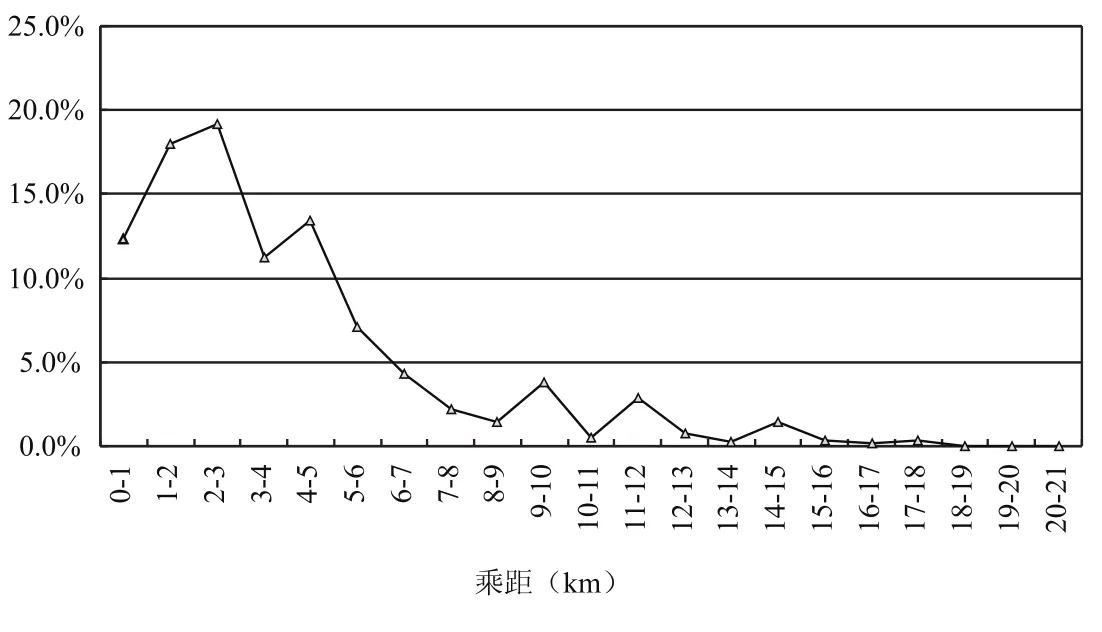
图3 西宁公交全日出行乘距分布Fig.3 Bus trip distance distribution of Xining city

3.4 距离概率函数确定

研究拟采用图3的全市公交乘距分布对每条线路进行了距离概率分布下的OD反推.当然,最好对每条线路采用不同的、且与各自适应的乘距分布概率进行OD反推.但问题是如何得到这些线路各自的距离分布?如果通过调查可以获取各线路的出行距离分布,必然以其OD已知为前提.显然,每条线路采用不同出行距离分布的方法并不可行.

4 单条线路OD反推分析

4.1 过客、上下客及OD分析

表1为等概率推算下的1路下行方向的OD表.图4为1路下行方向的等概率OD反推后的模拟客流与调查客流比较,图5为其上下客分布情况.对比图2可知,模型可以较好地拟合该线路方向的上下乘客分布.

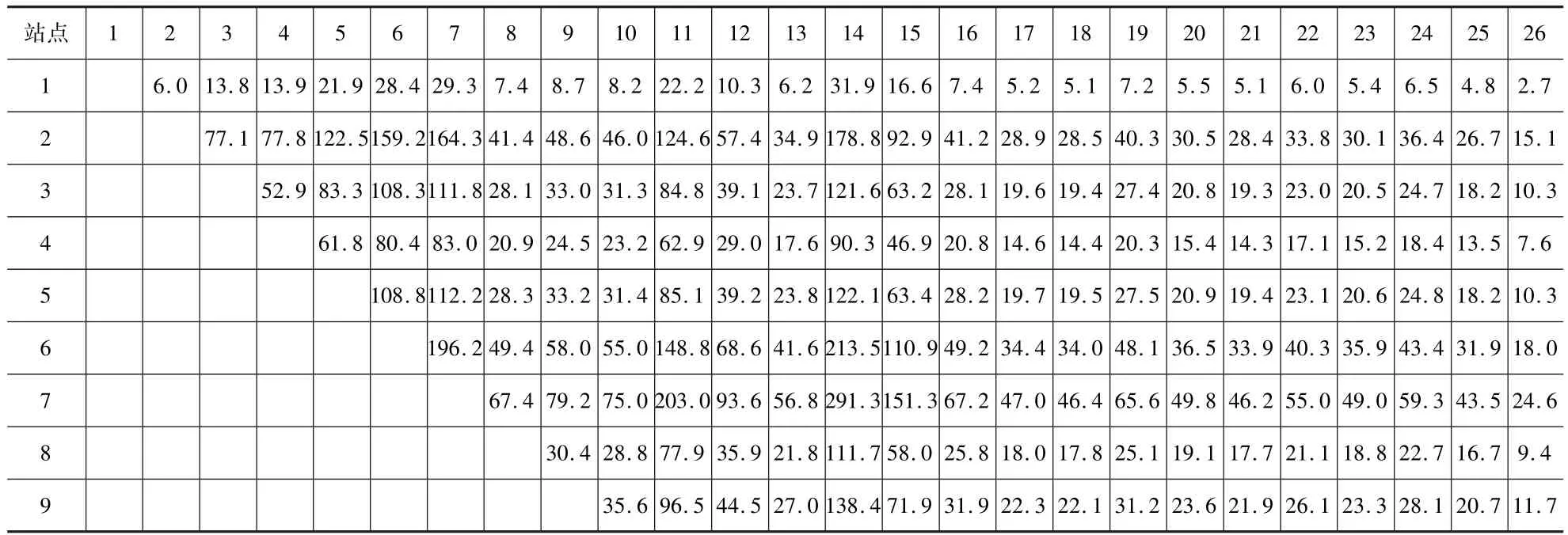
表1 等概率反推公交OD矩阵(1路下行)Table 1 Bus OD Matrix Estimation in equal probability(bus line one)

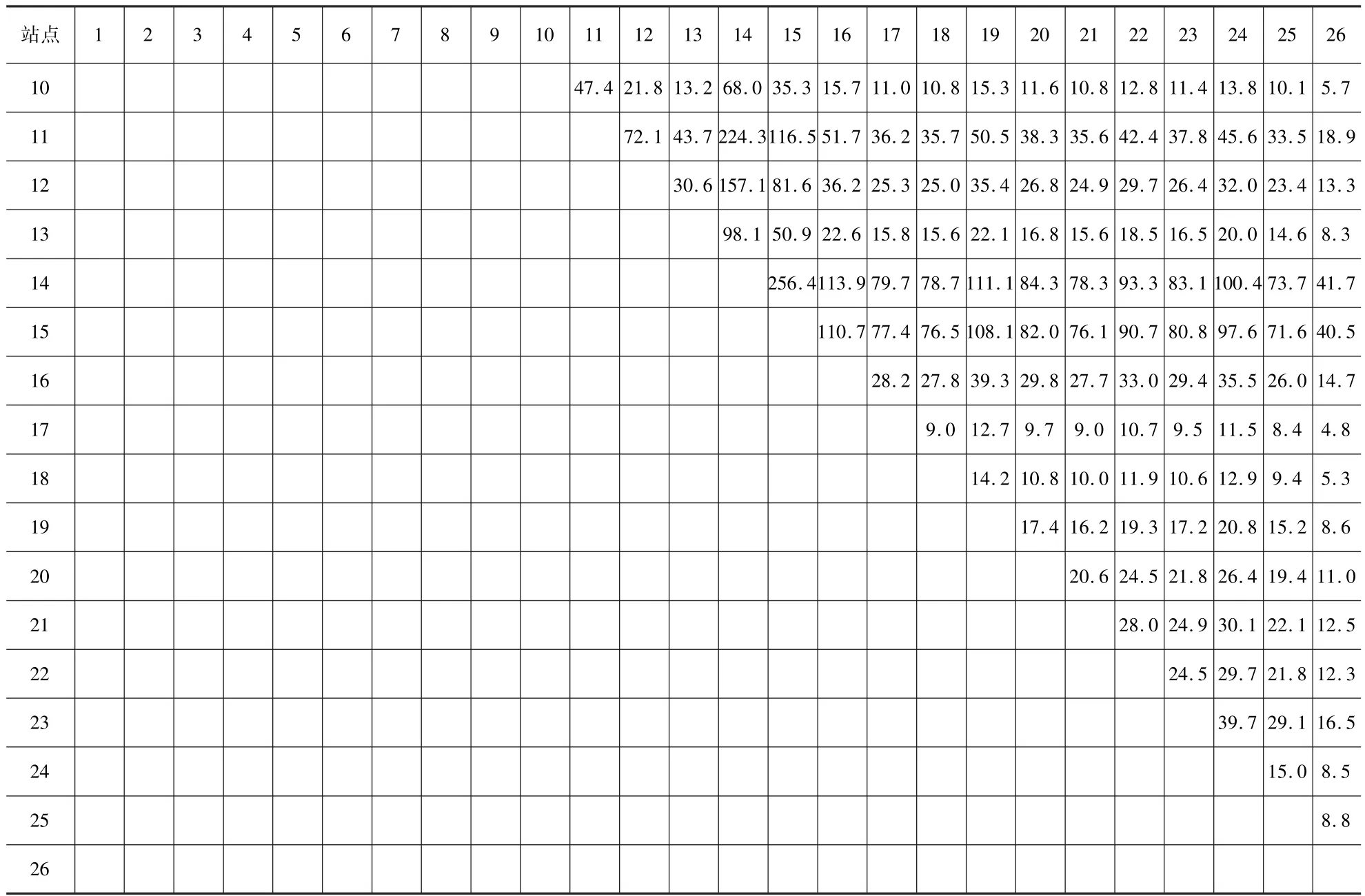
续表

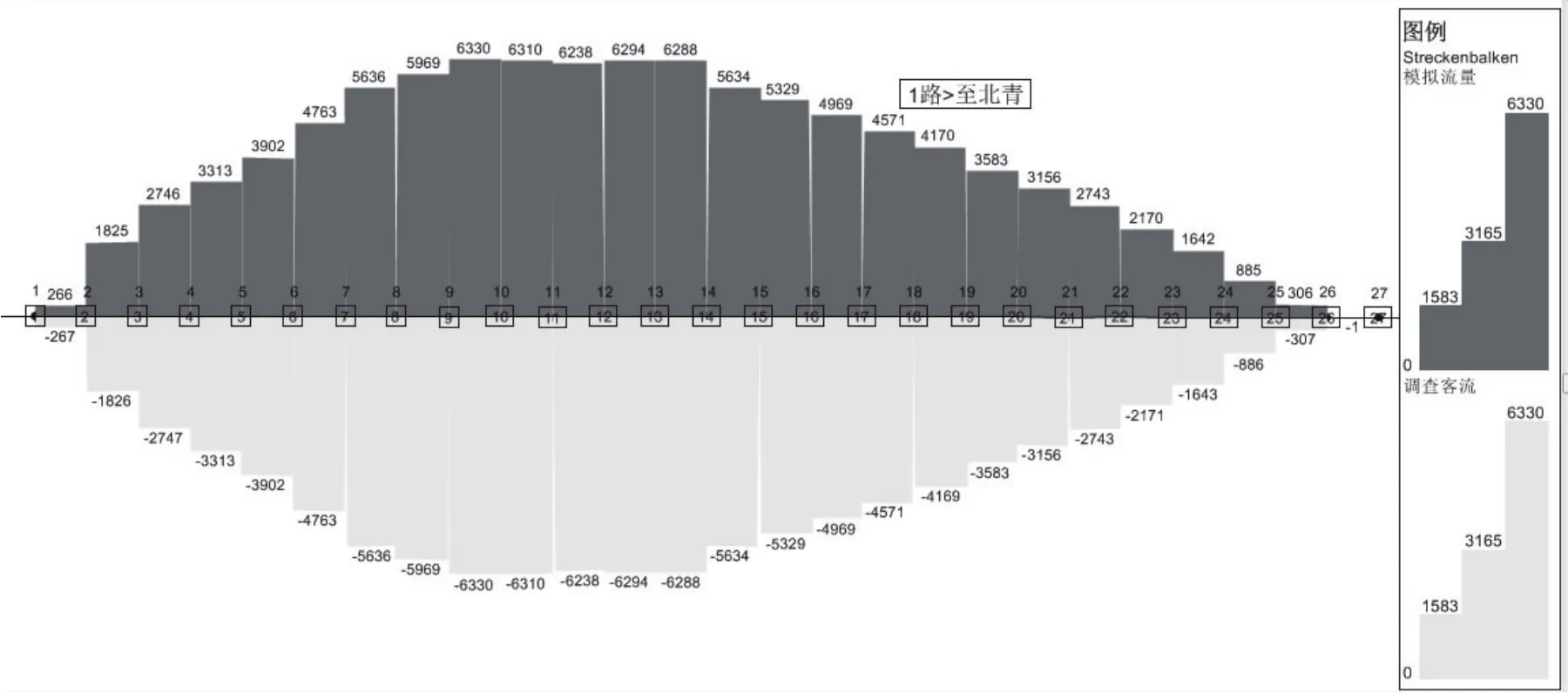
图4 借助VISUM模型等概率反推线路OD得到的模拟客流与调查客流比较(1路下行)Fig.4 Passenger flow simulation by VISUM equal probability model compared with survey(Bus line 1 down)

4.2 出行距离分布拟合分析

对于1路下行,也可按图6、图7所示的距离分布1、距离分布2和图3所示的调查分布,按距离概率、等概率分布(平均分布)进行OD推算.由图8可见各种分布下的推算出行距离分布差异较大.按平均分布,近距离出行比例较大.按距离概率分布进行OD反推,比平均距离下更能表现出近少、中多、远少的特点.但其误差并不比平均概率分布小多少.

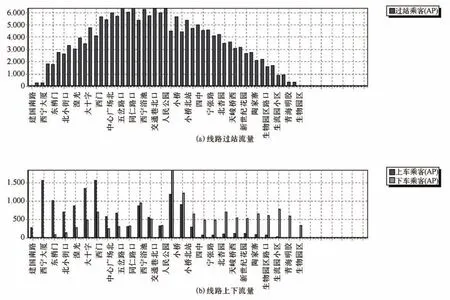
图5 模拟站点等概率反推获得的上下客和流量分布(1路下行)Fig.5 Passenger flow,Boarding and alighting Passenger by VISUM equal probability model(Bus line 1 down)

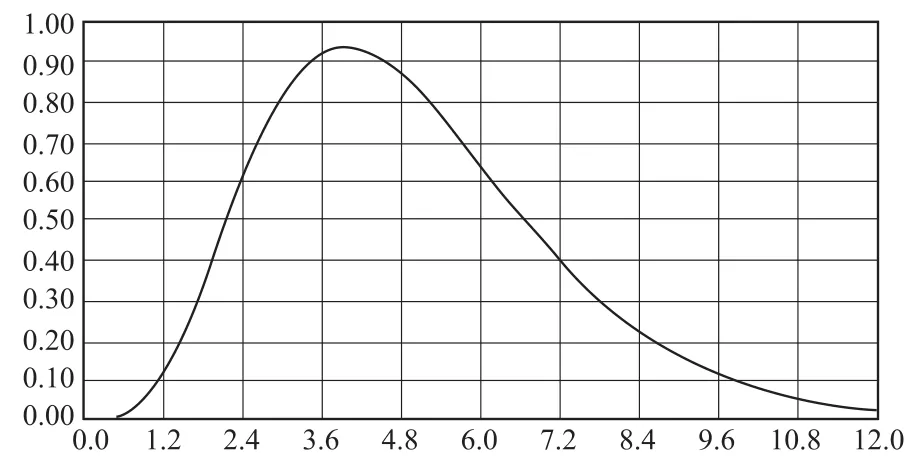
图6 假定距离分布1Fig.6 Assumed distance distribution 1

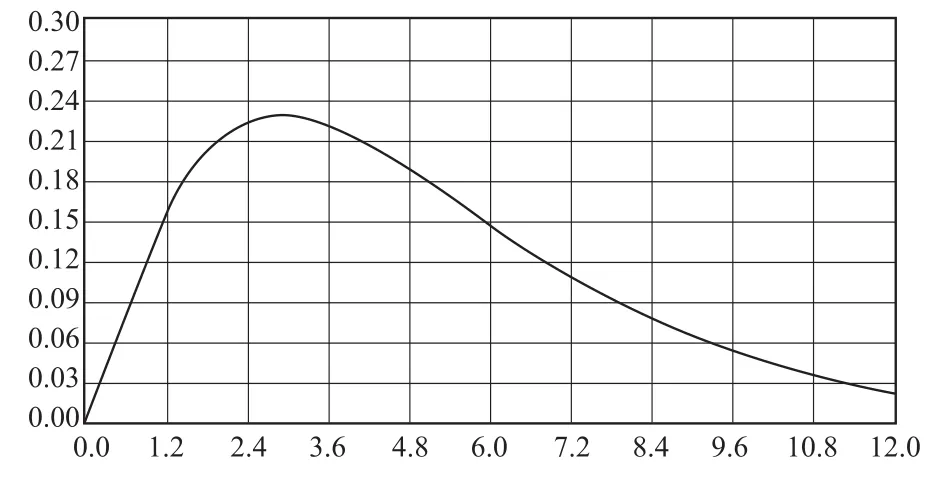
图7 假定距离分布2Fig.7 Assumed distance distribution 2

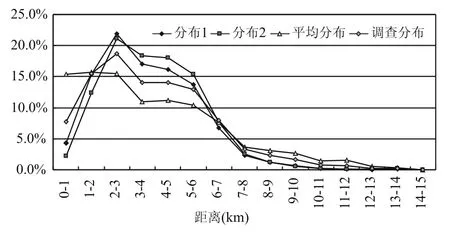
图8 不同出行距离分布的出行距离反推结果(1路下行)Fig.8 Simulated results according to distribution of different travel distance distribution(Bus line 1)

5 全市公交线网OD反推与公交现状模拟

5.1 基于线路OD反推的交通小区OD推算

采用分方向单线路等概率OD反推的方法,可得到全市64条线路的128组OD分布.同样也可采用图3所示的距离分布,得到全市各线路OD(距离概率分布法).基于全市64条线路的OD反推,可通过站点与交通小区的对应关系将站点OD发生与吸引归并至交通小区;对于介于两个交通小区之间的站点,采用相关交通小区的居住人口、就业岗位、建筑面积等因素进行加权分配;从而将各线路OD转化为交通小区OD,得到基于交通小区的全日公交OD.

5.2 基于线路OD反推的全市公交客流模拟分析

在全日等概率OD反推的基础上,可以得到全日城市公交客流量分布.与现状随车调查的客流分布对比,可得到全日模拟各路段客流量与调查客流量的误差分析.对于距离概率反推,也可得到相应成果.研究对大于0.25、0.50、0.75万人次/日的路段进行了误差统计.等概率、距离概率下的分析结果如表2、表3所示.由表可见,等概率分布下的OD推算在路段流量拟合精度方面优于距离概率分布的OD反推.

表2 等概率分布下的路段客流量模拟误差分析Table 2 Error analysis of simulation passenger flow of link according to equal probability distribution

表3 距离概率分布下的路段客流量模拟误差分析Table 3 Error analysis of simulation passenger flow of link according to probability distribution related to distance

5.3 各线路OD推算下的出行距离分布

可由等概率反推64条线路128个模型的公交出行路径、流量,对所有线路的出行距离、次数进行数据统计,得到出行距离分布,图9将其简称为“等概率反推”.根据等概率反推得到全市OD矩阵,通过全市的公交模型,进行公交客流分配,经统计分析可得到分配后的出行距离分布,简称“等概率反推分配结果”.同理,可对距离概率进行类似分析,如图10所示.

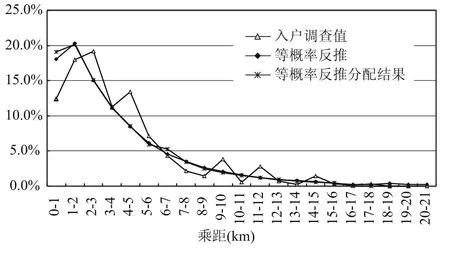
图9 等概率OD反推下的出行距离分布比较Fig.9 Distribution of trip distance of equal probability distribution

对比图9和图10,可知距离概率反推得到的距离分布更接近居民出行调查的距离分布.“等概率反推”、“等概率反推分配结果”、“距离概率反推”、“距离概率反推分配结果”的乘距分布存在差异.更为明显的是,“距离概率反推”与“距离概率反推分配结果”乘距分布的差异较大;而“等概率反推”与“等概率反推分配结果”的差异较小(见图11).图11中“距离概率反推分配结果”的乘距分布向“等概率反推”、“等概率反推分配结果”靠近.距离概率反推OD的模型分配后的公交平均出行距离为4.27 km,等概率分布下为4.54 km,现状随车调查值为4.63 km.等概率分布的平均出行距离推算结果更接近随车调查值.

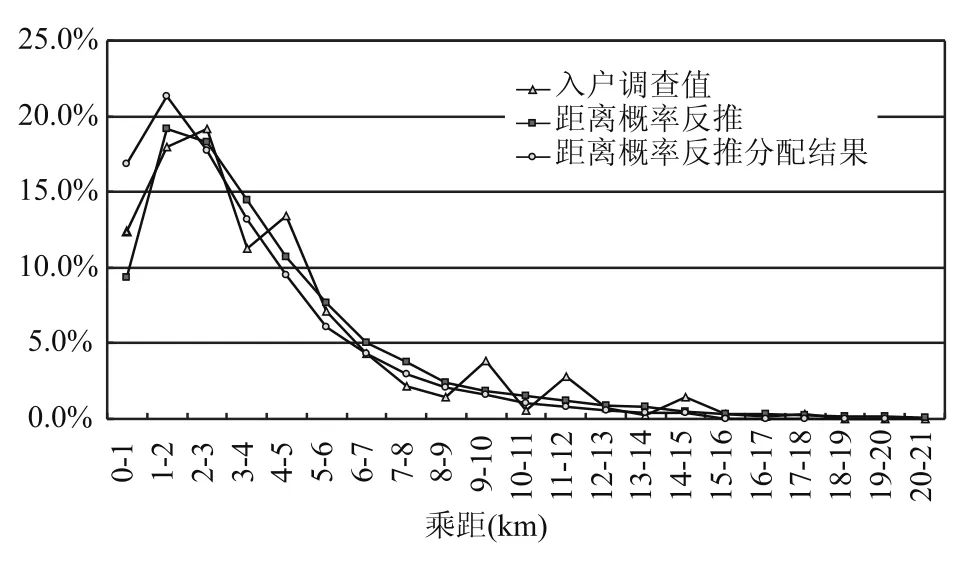
图10 距离概率OD反推下的出行距离分布比较Fig.10 Distribution of trip distance of probability distribution related to distance

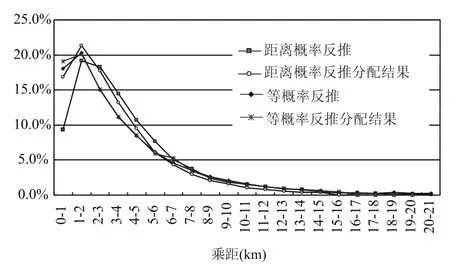
图11 距离反推与等概率反推距离分布的比较Fig.11 Distribution of trip distance of probability distribution related to distance with equal probability distribution

5.4 OD反推效果产生差异的原因分析

由调查可知公交乘距分布会表现为近少、中多、远少的特征.可以认为某一站(i)上车的乘客在后续各站(i-j)的下车概率也服从这一规律.在采用重力模型进行OD推算的过程中,已将后续各站的下客人数作为后续各站下客概率的影响因素,而该因素已包含了距离分布影响、下客站周边的交通吸引影响.在上述基础上,再考虑出行距离分布特征对后续各站乘客下车概率的影响,则过多的受到了出行距离因素的影响.平均概率法虽然存在第一站下车的乘次偏高的问题,但由图11的相关分析可知,交通分配结果对该偏差进行了纠正.

无意排斥距离分布因素在公交OD反推中的作用,但至少对于西宁,在各站乘客下车人数数据已经获得的基础上,等概率分布下的公交OD反推更具现实意义.

6 研究结论

公交OD反推技术是获取公交规划关键基础数据的有效方法.该方法一方面可以大幅度降低公交出行调查的工作量与调查成本,另一方面可以有效提高调查数据的利用率;为公交规划提供更为有效的技术支撑.但乘客在各站的下客的概率影响因素较多,把握并合理利用其规律是公交OD反推的关键.即便采用OD反推技术,公交流量模拟依然具有较大的误差,这与模型中关于车上舒适度、道路拥挤、站点周边用地性质等因素考虑的不足,以及线路之间的竞争、模拟交通小区的连接线与实际出入口的差距等因素有关,相关研究还有待深化.

[1]吕智林,范炳全,张林峰,等.基于梯度法的OD矩阵估计和应用研究[J].上海理工大学学报,2004,26 (6):553-556.[LV Z L,FAN B Q,ZHANG L F,et al. OD matrix estimate based on gradient approach and research on its application[J].Journal of University of Shanghai for Science and Technology,2004,26(6): 553-556.]

[2]武荣桢,罗京.基于公交站点上下客人数反推OD矩阵的概率论模型研究[J].交通标准化,2009(196): 123-126.[WU R Z,LUO J.TransitOD matrix estimation method based on passenger boarding and alighting[J].Transport Standardization,2009(196): 123-126.]

[3]周雪梅,杨熙宇,吴晓飞.基于IC卡信息的公交客流起止点反推方法[J].同济大学学报,2012,40(7): 1027-1030.[ZHOU X M,YANG X Y,WU X F.Origindestination matrix estimation method of public transportation flow based on data from bus integratedcircuit cards[J].Journal of Tongji University,2012,40 (7):1027-1030.]

[4]邹亮,张孜,朱玲湘.基于手机定位的公交OD获取方法研究[J].交通信息与安全,2011,29(5):122-126. [ZOU L,ZHANG Z,ZHU L X.Public transportation OD data collection based on mobile location technology [J].Journal of Transport Information and Safety,2011, 29(5):122-126.]

[5]窦慧丽,刘好德,杨晓光.基于站点上下客人数的公交客流OD反推方法研究[J].交通与计算机,2007, 25(2):79-82.[DOU H L,LIU H D,YANG X G.OD matrix estimation method of public transportation flow based on passengerboarding and alighting[J]. Transport and Computer,2007,25(2):79-82.]

[6]刘翠,陈洪仁.公交线路客流OD矩阵推算方法研究[J].城市交通,2007,5(4):81-84.[LIU C,CHEN H R.Study on OD matrix estimation of trans it passenger flows[J].Urban Transport of China,2007,5(4): 81-84.]

[7]朱从坤,陈瑜.基于公交客流OD反推的公交乘客乘车站数分析[J].辽宁交通科技,2005(3):52-54. [ZHU C K,CHEN Y.Public transport passengers boarding station counting analysis on OD matrix estimation[J].Liaoning Communication Science and Technology,2005,5(3):52-54.]

Bus OD Matrix Estimation by VISUM Model: Case of Xining of China

CAI Juna,LIU Kaib,LIU Lian-liana
(a.School of Architecture&Fine Art;b.School of Transportation and Logistics,Dalian 116024,Liaoning China)

The origin-destination(OD)matrix is important for transit line planning and optimizing.It also provides an effective way to get the bus OD matrix data.However,the studies on city's whole transit lines are still very limited.Based on the boarding,alighting and thorough passenger data of every bus line in Xining city,the paper develops a bus OD matrix estimation model with VISUM by the equal alighting probability and probability related to riding distance.In this model,the OD matrix of traffic zone is estimated from each bus line.Then,the reliability of the OD matrix estimation is analyzed by comparison of two kinds of road-passenger flow:one is obtained from traffic assignment,and the other comes from traffic survey of bus line.The result indicates that the OD matrix estimation by method of equal alighting probability is accurate and effective.Finally,it draws the conclusion that the alighting probability at bus stop is influenced by many factors,and its mechanism should be analyzed and used reasonably.

urban traffic;OD matrix estimation;VISUM;bus;passenger boarding and alighting

U121

A

U121

A

1009-6744(2013)01-0049-08

2012-08-15

2012-11-08录用日期:2012-11-20

国家自然科学基金面上项目(51278075);国家自然科学基金青年基金(51008050);中央高校基金科研业务费专项重点项目(DUT12ZD203).

蔡军(1970-),男,山东平原人,副教授、博士.

*通讯作者:caimans@126.com