基于沿途补货的多配送中心动态需求VRP建模及优化

张景玲，王万良，赵燕伟

（1．浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310012；2．浙江工业大学 计算机科学与技术学院，浙江 杭州 310012）

0 引言

根据配送系统中配送中心数目的多少，车辆路径问题［1］（Vehicle Routing Problem，VRP）有单配送中心和多配送中心之分。现有研究主要集中在单配送中心问题上，多配送中心问题国内近几年才有研究。对于多配送中心VRP，不能简单地直接使用单配送中心路径的思路和方法，必须在深入研究其特点的基础上，选择合适的方法进行求解。

多配送中心VRP的求解目前主要有两种方法：

（1）将多配送中心VRP转化为多个单配送中心VRP，然后进行优化组合，该方法的研究重点在多配送中心的分离策略和最后解的优化组合方案选择上，但是较难确定合适的分区方案，从而比较容易使问题限于局部最优。文献［2］研究了多车型取送混合的多配送中心VRP；文献［3］结合Sweep算法和Saving算法，给出了多车场转化为单车场的处理方法，但没有给出分解点δ的设定标准，且分配的结果并不十分理想。

（2）将多配送中心VRP本身看作一个复杂的组合优化问题进行研究，该方法的研究重点集中在如何合理地缩小搜索空间和简化求解步骤上，对算法的要求比较高。文献［4］考虑车辆最大行驶距离的约束条件，建立多车场满载条件下的协同运输问题的数学模型，设计了基于贪婪算法的两阶段启发式算法；文献［5］研究了以最快完成为目标的多车场多车型VRP的变异蚁群算法；文献［6］研究了基于并行蚁群算法的多配送中心VRP；文献［7］提出一种基于启发式的整数规划方法来求解多配送中心VRP，取得了较好的结果；李延辉和刘向［8］采用第（2）种方法研究了基于沿途补货策略的开放式VRP，并提出了带补货控制因子的蚁群算法用于求解该问题，但是蚁群算法是基于单点搜索的算法，常常搜索的时间较长，且容易出现停滞现象。

已有文献对多配送中心问题的研究大多在静态环境下进行，与车辆调度相关的信息在路径规划之前已知，输出是一条预先规划好的路线；然而现实中在路径规划前，这些信息并不能完全已知，这类问题称为动态VRP，其输出路线随信息的变化动态调整。文献［9］将动态VRP转化为一系列静态子问题，提出了改进的遗传算法（Genetic Algorithm，GA）进行求解，并与禁忌搜索、蚁群系统进行比较，说明了算法的有效性；文献［10］研究了多期动态VRP，提出三阶段滚动时域启发式算法解决该问题，计算结果表明，该方法可以产生合理运行时间内的高质量解决方案；文献［11］研究了具有实时顾客需求和动态网络的VRP，建立了对应动态环境的静态转换模型，提出一种能同时利用演化算法全局优化能力和蚁群算法局部搜索能力的混合智能优化算法（Intelligent Optimized Algorithm，IOA），取得了较好的实验结果；文献［12］提出一种改进的大领域搜索算法求解有时间窗的动态VRP，通过事件触发将动态调度转换为一系列静态子问题进行求解，所提算法能快速获得问题的解；文献［13］综述了动态取送货VRP的架构及求解策略，指出动态VRP的两种优化策略——重优化策略和局部优化策略。

本文考虑顾客需求的动态性，在文献［8］的研究基础上提出了基于沿途补货策略的多配送中心动态需求VRP。通过将计划周期分片，将动态调度问题按照时间轴依次分解为一系列的静态调度子问题，建立了该问题基于时间轴的多阶段数学规划模型，为方便问题的描述，采用一个两阶段的模型来体现：第一阶段根据已知客户信息建立预优化模型；第二阶段加入顾客实时信息，引入虚拟配送中心的概念，建立重调度模型。多阶段的模型是在第二阶段模型上进行的扩展。对多配送中心问题，本文采用第二种方法求解，将其看作一个配送路径跨区域的组合优化问题。鉴于量子进化算法［14］求解效率高、收敛速度快、全局寻优能力强等性能，本文将其引入动态VRP的求解，提出了自适应免疫量子进化算法，并设计了最邻近法结合贪婪规则的沿途补货策略。

1 多配送中心动态需求VRP数学规划模型

1．1 问题描述

沿途补货的多配送中心动态需求VRP描述为：有M个车场，各自拥有容量为bk的车辆Km（m＝1，2，…，M）辆，对L个用户进行货物配送，用户i的货物需求为di（i＝1，2，…，L），di＜bk，每个用户可由任何一个车场的车辆服务，但只能由一辆车服务一次，每辆车完成任务后无须返回原车场。在服务的过程中，存在客户需求的动态变化：考虑新客户的出现及原有客户需求量的变化。

（1）沿途补货策略 从任一配送中心始发的货车可在途经的多个配送中心补充货物，并对整个联合区域内的缺货需求点进行货物供给。当车载货物配送完或即将配送完，即无法为下一客户配送货物时进行补货。

（2）目标 要求一个合适的车辆调度方案，能够满足所有用户的需求，并使车辆总的运输成本最低。针对动态调度问题，本文建立了两阶段数学模型：第一阶段为预优化模型；第二阶段为重调度模型。

1．2 数学规划模型

（1）第一阶段预优化模型

用户编号为1，2，…，L；配送中心编号为L＋1，L＋2，…，L＋M；Fk为发车的固定费用，k∈｛1，2，…，Km｝，m∈｛L＋1，L＋2，…，L＋M｝；cij为从i地到j地的运输成本，i，j∈（1，2，…，L，L＋1，…，L＋M），当i，j同时为车场时cij＝∞，即禁止从车场到车场；ωmijk为配送中心m的车辆k从i地到j地的运输量，i，j∈（1，2，…，L，L＋1，…，L＋M），m∈｛L＋1，L＋2，…，L＋M｝，k∈｛1，2，…，Km｝。

定义决策变量：

则沿途补货的多配送中心动态需求VRP数学模型表示如下：

目标函数：

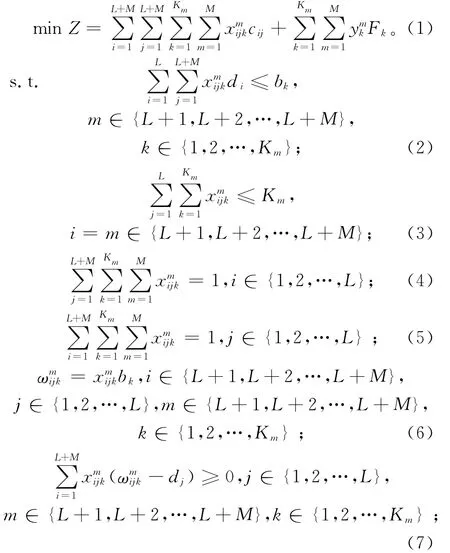
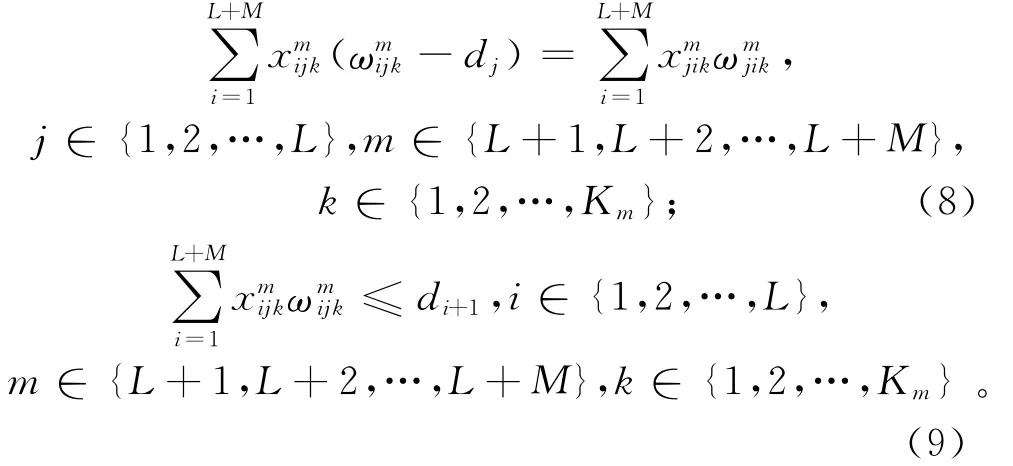
其中：式（2）保证车辆的容量限制；式（3）表示各配送中心派出的车辆数不超过该车场所拥有的车辆数；式（4）～式（5）保证每个客户仅被一辆车访问；式（6）表示从配送中心出发的货车的运输量为货车的载量，即满载出发，它是式（7）～式（9）的初始条件；式（7）表示进入任一客户之前，货车有足够供给这个客户的货物；式（8）表示货车经过客户点j后运输量发生改变的关系式；式（9）表示货车现有运输量无法为下一需求点配送货物时进入仓库补货。

（2）第二阶段重调度模型

在第二阶段的开始调度时刻，预优化阶段调度的车辆因为驶离配送中心，已服务了部分客户，车辆的剩余载重量变得不相同，并且由于车辆位于客户处，直接调度将无法进行，本文引入虚拟配送中心的概念，将车辆所在的客户点设为虚拟配送中心，建立如下的多配送中心多车型VRP模型。

N表示第一阶段未服务客户与第二阶段新客户的总数量，假设第一阶段派出车辆数为Hm，派出车辆的剩余车载量为bmh（m＝1，2，…，M，h＝1，2，…，Hm），则用Hm表示虚拟配送中心数量，虚拟配送中心编号为N＋M＋1，N＋M＋2，…，N＋M＋H，原配送中心编号为N＋1，N＋2，…N＋M，新派车Tm辆。

目标函数：

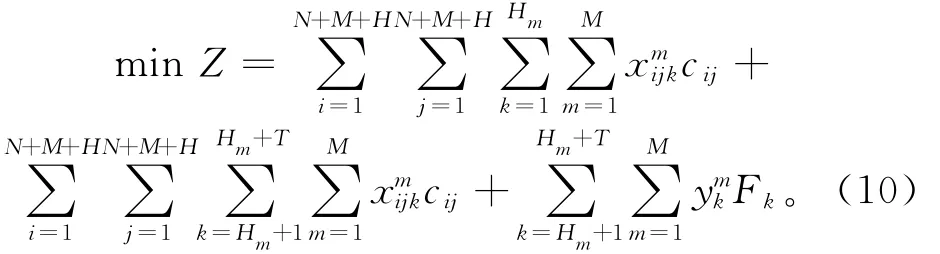
式（10）包括三部分：①第一阶段派出车辆对第一阶段未服务客户和第二阶段新客户的运输成本；②第二阶段新派出车辆的运输成本；③第二阶段新派出车辆的发车成本。

2 多配送中心动态需求VRP的自适应免疫量子进化算法

2．1 自适应免疫量子进化算法设计

量子进化算法在进化的同时不可避免地会出现退化的现象，引入免疫算子进行线路内（同一个车辆路径中）和线路间（不同车辆路径中）的再优化，在算法中加入对问题的先验知识能有效地加快算法的收敛速度，提高解的质量。具体操作如下：

（1）提取疫苗 根据问题的特征信息提取，对于VRP，根据最邻近法则选择离节点最近的点作为该节点的疫苗，从而得到各节点的疫苗矩阵。

（2）免疫算子

1）疫苗接种 疫苗接种是染色体基因的调整过程，根据选取的疫苗局部调整染色体基因顺序，实现线路内和线路间路线的调整。以一定的概率选择染色体，将接受检查的基因点的后继点与疫苗点的位置进行交换，当后继点为疫苗点时不接种，如下例所示。其中加粗的数字表示接种疫苗的节点，加阴影的数字表示该点的疫苗。

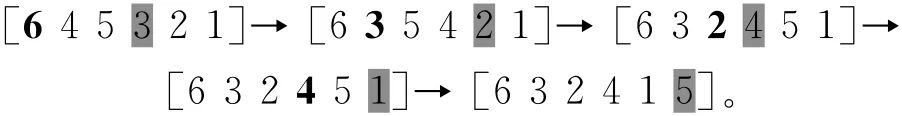
在提取疫苗时，可能存在不同节点对应同一个疫苗的情况，因此在疫苗接种的过程中有可能出现疫苗点在该点前面的情况，此时不接种，继续下一点。如下例所示。

2）自适应接种 在量子进化算法中混合免疫算子可以提高量子进化算法的局部搜索能力，但是也需要更多的局部搜索时间，从而增大了算法的时间开销，这对于动态调度是不适合的。因此为减少算法的运行时间，不对所有的个体接种疫苗，而是根据个体适应度的高低进行有选择地接种，适应度高的个体接种的概率大，适应度低的个体则接种的概率小。本文设计了一种随个体适应度大小而变化的自适应选择概率pl，

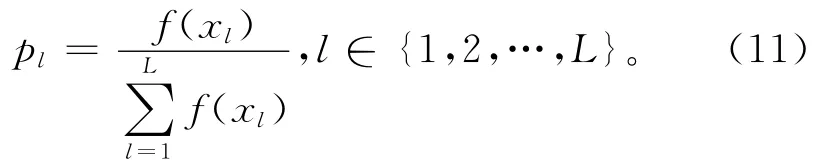
以概率pl选择个体xl进行疫苗接种，f（xl）为个体xl的适应度，l表示种群的大小。

3）免疫选择 选出最优个体，当该个体比父代最优个体更优时选用该个体；当其比父代劣时，说明免疫操作没有起到作用，选用父代最优个体。

2．2 自适应免疫量子进化算法流程

针对上述建立的动态需求VRP的两阶段数学规划模型，采用“预优化路线的制定＋动态优化调整”的两阶段求解策略［15］，分别采用自适应免疫量子进化算法（Adaptive Immune Quantum－inspired Evolutionary Algorithm，AIQEA）进行求解，具体步骤如图1所示。在重调度阶段解码时先派第一阶段的车辆，若第一阶段车辆无法满足，则启用新车。

算法的主要操作：

（1）基于问题特征的编码 采用基于客户序列的编码方法［15］。

（2）初始化种群 随机产生拥有多个染色体的初始种群，根据上述编码方案，染色体就是L组且每组都包含n个量子比特的串。量子比特各位采用随机初始化，即αi和βi均为由计算机随机产生0，1之间的任何数。

（3）基于沿途补货策略的解码 解码过程采取“先客户，再配送中心”的两步走方法：

步骤1 产生客户服务的先后序列。

步骤2 形成配送路径。对于沿途补货的VRP，设计了一种基于最邻近法结合贪婪规则的补货策略：首先按客户序列表顺序服务客户，利用最邻近法则寻找离当前客户点最近的配送中心作为实际发车的配送中心或沿途补货的配送中心；其次结合贪婪规则判断是否需要补货，如果前一点到其最近配送中心的距离加该点到其最近配送中心的距离之和小于该点到其最近配送中心的距离加固定发车成本之和，说明补货的费用低，则到最近的配送中心补货，否则重新派一辆车，若所需车辆数超过已有车辆数，则该路径为不可行解。例如对于一个有11个客户、3个配送中心的问题，解码方法具体如下：

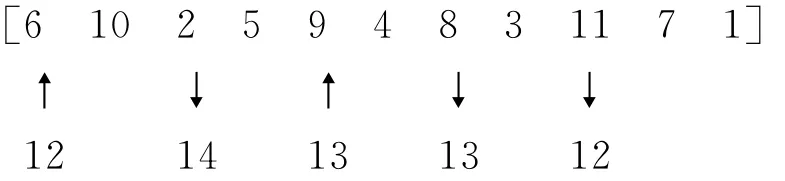
以数字“0”表示补货的配送中心，如上形成路线：12—6—10—2—14—0—5—13—9—4—8—13—0—3—11—12—0—7—1。其中14—0表示配送中心14作为一次补货点，同样13—0，12—0中配送中心13，12也是补货点。

（4）适应度计算 对种群中的各个染色体解码后，分别根据第一阶段式（1）和第二阶段式（10）求得目标函数值Z；若染色体对应不可行解，则赋予Z一个很大的整数。令染色体的适应度函数为Fitness＝1／Z。

（5）量子旋转门更新 在量子进化算法中，量子门是最终实现进化操作的执行机构，最常用的为量子旋转门，进化过程由量子旋转门更新量子位概率幅来实现，具体可参见文献［16］。

3 实验结果与分析

3．1 实例测试

本文所有程序采用Java语言编写，在Pentium®D CPU 2．8GHz，1．0GB的内存上运行。某物流配送公司实际的配送过程可归结为开放式、带容量约束、多配送中心的动态需求VRP，在配送的过程中，可就近在公司的其他分配送中心补货。该物流系统拥有4个配送中心，车载量为8t，初始客户数为50个，各客户点的坐标和需求如表1所示，表中1～50为客户点编号，51～54为配送中心编号。

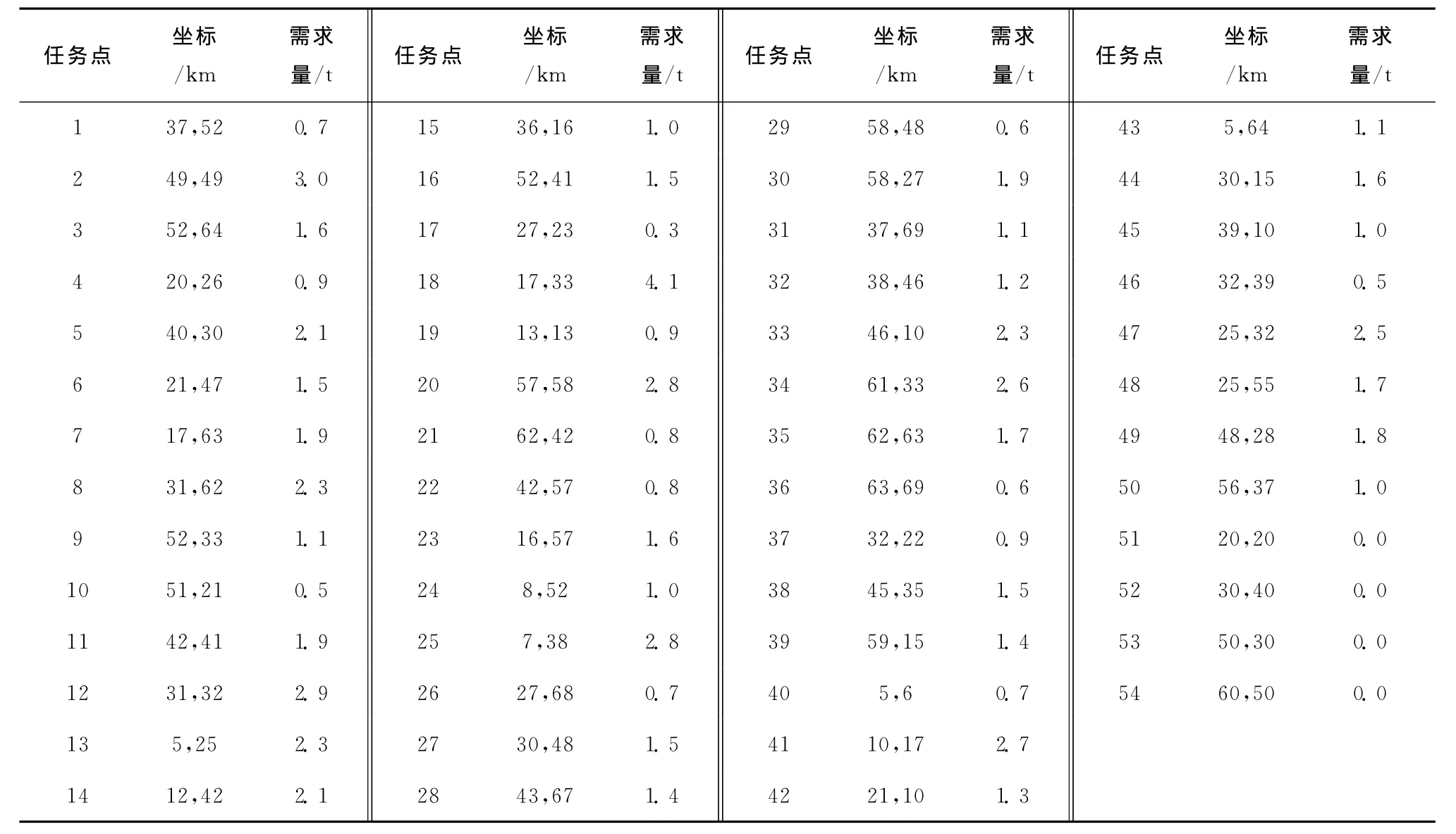
表1 初始客户点信息

首先对初始客户点运用自适应免疫量子进化算法进行求解，结果如表2所示。在表2中，如果配送中心后面有0，则表示该配送中心为补货的配送中心。自适应免疫量子进化算法在预优化阶段的收敛曲线如图2所示。

在时刻15更新客户需求信息，此时有10个新客户提出服务请求，其坐标和需求分别为a（12，43，2．3），b（16，4，1．4），c（21，61，1．2），d（58，74，0．4），e（55，40，1．4），f（62，74，2．0），g（12，75，1．6），h（25，58，2．4），i（77，50，1．2），j（32，68，1．1）。

由计算结果可知，此时配送中心已发出5辆车，分别位于点46（32，39），43（5，64），37（32，22），20（57，58），21（62，42），车辆的剩余载重量分别为0．7 t，4．2t，2．2t，5．2t，1．3t。客户点38，11，32，1，27，46，48，24，43，41，19，42，37，20，49，10，9，50，16 已服务。在重调度阶段，除去已服务客户点，未服务客户点和新需求点共40个，将此时车辆所在的点设为虚拟配送中心，原配送中心依然对客户服务，根据上文建立的第二阶段模型运用混合量子进化算法进行求解，迭代次数为2 000次，种群大小为50，计算结果如表3所示。可以看出，对于新加入的客户点，虚拟配送中心的车辆不仅将车上原有的货物配送完，而且参与第二阶段的补货。重调度阶段的收敛曲线如图3所示。

表2 初始客户优化路线

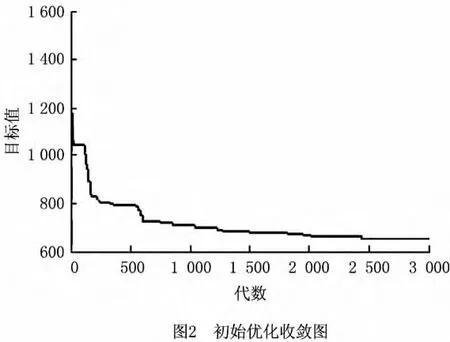
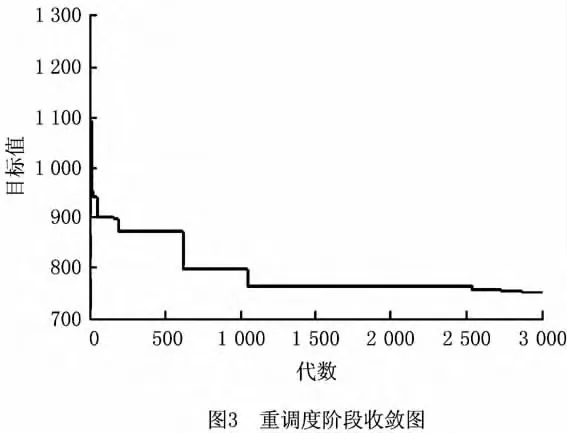
表3 重新优化路线

3．2 优化性能实验及分析

动态需求的多配送中心VRP缺少标准的测试实例库，研究者随机生成或在已有实例的基础上进行修改。本文预优化阶段测试实例的数据来自标准的多配送中心的实例库，所有实例可以从http：／／neo．lcc．uma．es／radi－aeb／WebVRP／上下载，p02（50，4）表示4个配送中心对50个客户进行配送服务。所选实例中客户点的数量从50～100，配送中心的数量也随之改变，分别代表不同类型的问题。实时优化阶段客户信息随机生成。第一阶段的优化结果如表4所示，图4是算法的收敛曲线图。

表4 初始客户优化路线

时刻15更新客户信息，由计算结果可知此时已完成和未完成的路线如表4所示，表中有阴影的数字表示重调度阶段的虚拟配送中心，位于该点前面的点为已经服务的客户点，之后的点为还未服务的点，括号中加字符边框的点表示该路线上车辆的剩余车载量。

重调度阶段，客户需求信息随机生成，随机生成客户坐标和需求量，优化结果如表5所示，图5是第二阶段自适应免疫量子进化算法的收敛曲线图。

表5 重新优化路线

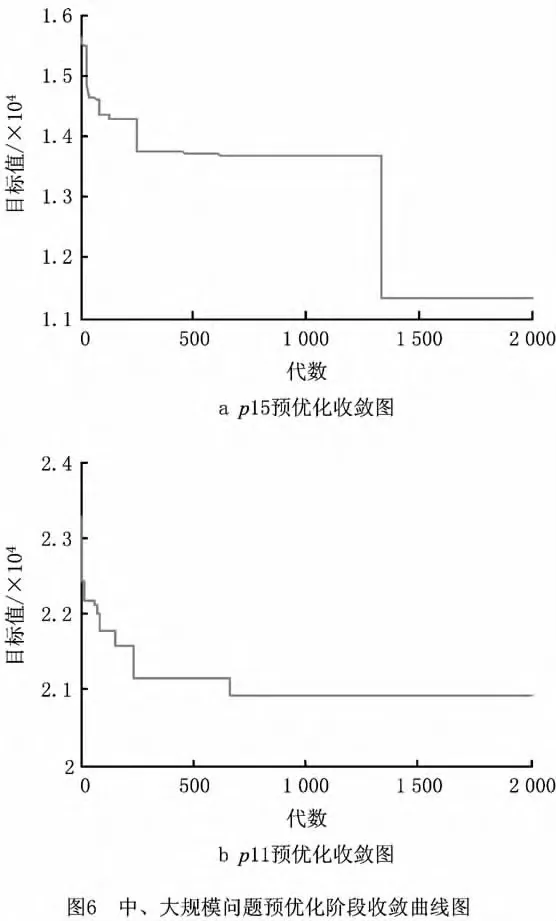
为了更好地检验算法的性能，从小、中、大规模分别对5个经典的实例进行了测试，每个测试实例均随机运行40次，其最优解、均值、标准方差和计算时间的统计结果如表6所示。从表6可以看出，求得的平均值接近最优值，算法的优化性能较好，标准方差相对平均值较小，算法的稳定性能较好。图6和图7分别为两个阶段算法的收敛曲线图。

用Xk表示自适应免疫量子进化算法第k次迭代时的状态。由算法的迭代过程可知，k＋1时刻的状态Xk＋1取决于Xk，与以前的状态无关。可以用齐次Markov链描述整个迭代过程，自适应免疫量子进化算法伴随的马氏过程能够收敛到问题的最优解。

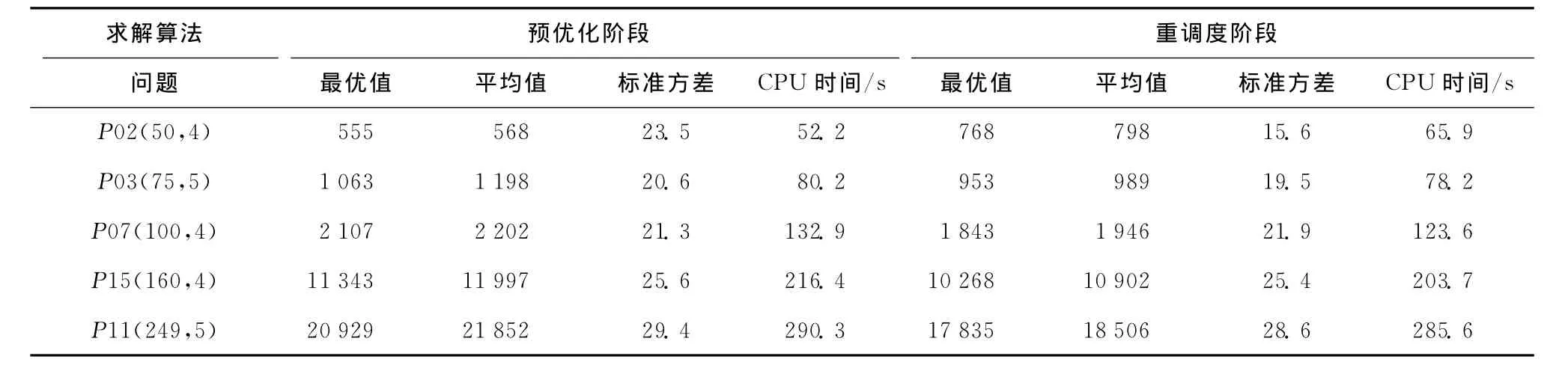
表6 算法结果统计

3．3 沿途补货策略分析

对于多配送中心的VRP，本文采用沿途补货的策略，当配送车辆装载的货物无法为下一个配送点服务，即车上的装载货物已配送完或即将配送完时，车辆进入配送中心补货。采用此策略可减少实际使用的车辆数，降低发车成本，特别是在有动态需求的情况下，当新的需求点插入，配送车辆剩余载货量小于该新需求点的需求量时，就可以到就近的配送中心补货，而无需从配送中心新派一辆车，表7所示为沿途补货策略和基于大范围统一调度策略的结果比较。从表7可以看出，采用沿途补货策略比基于大范围统一调度策略所需的车辆数少，降低了配送中心的固定成本。

3．4 算法比较分析

对于沿途补货的动态需求VRP，目前尚不能找到类似的算例与算法进行直接比较，为了比较算法的性能，在重调度阶段分别采用本文所提的AIQEA与最邻近插入法，以及文献［9］中的遗传算法相比较。最邻近插入法采用局部优化策略，将新的客户需求就近插入预优化的路线中，文献［9］中的遗传算法对动态问题的求解取得了较好的优化结果，计算时选用的参数与文献相同。

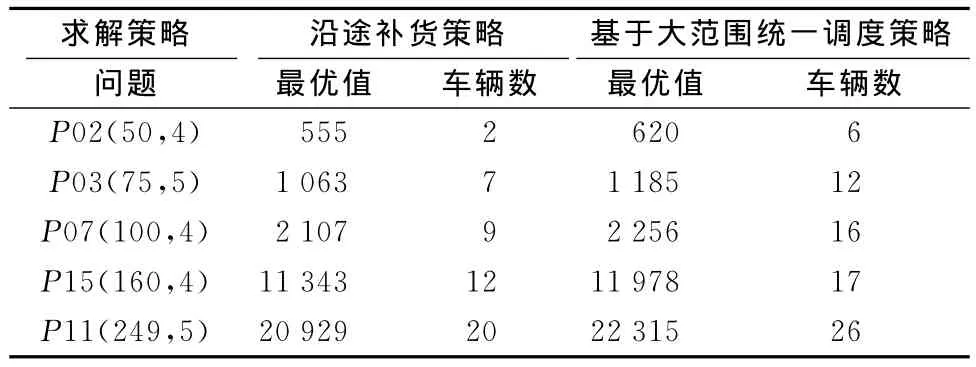
表7 沿途补货策略和基于大范围统一调度策略比较

表8所示为优化结果和优化时间的对比。可以看出，本文采用的AIQEA能更好地求得问题的解，与最邻近插入法相比，AIQEA能对第二阶段的客户进行全局求解，从而获得成本更低的调度方案，虽然比最邻近插入法求解的速度慢，但能满足动态问题的时间要求。相比动态车辆路径问题的遗传算法（Dynamic Vehicle Routing Problem－Genetic Algorithm，DVRP－GA），本文算法除问题P11（249，5）外，其他结果均较优。

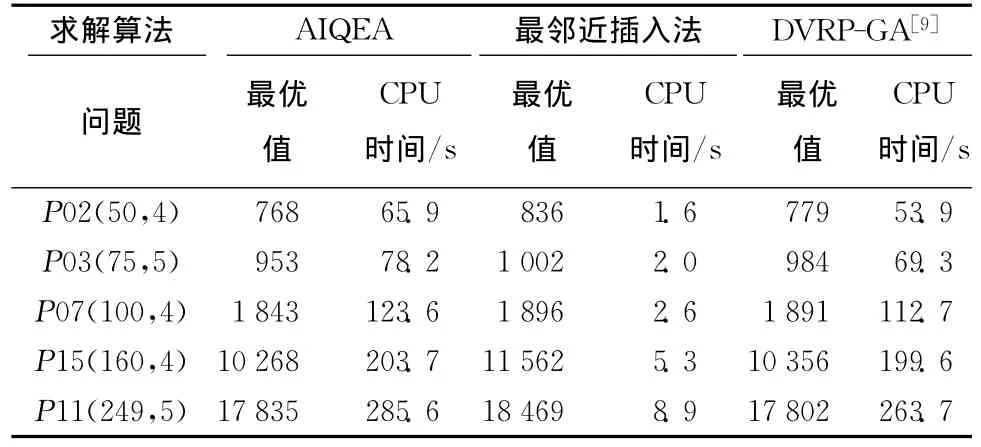
表8 算法结果比较

4 结束语

本文针对多配送中心动态需求VRP，在已有文献提出的基于沿途补货策略的静态模型基础上，考虑顾客需求的动态性，进一步探讨该策略在动态环境下的适用性，首次提出了基于沿途补货策略的多配送中心动态需求VRP，并建立了该问题的两阶段的数学规划模型。对于沿途补货策略，设计了一种最邻近法则来控制车辆补货的解码方法，可减少配送中心所使用的车辆数，从而可降低配送中心的运行成本；并设计了一种自适应免疫量子进化算法，在量子进化算法中引入免疫算子进行线路内和线路间的再优化，从关于问题的先验知识中提取疫苗，充分利用了问题的先验知识，有效地加快了算法的收敛速度，提高了解的质量，同时为适应动态调度对算法实时性要求较高的特点，在疫苗接种的过程中设计了一种随个体适应度大小而变化的自适应选择概率，适应度高的个体接种的概率大，适应度低的个体则接种概率小，从而减少了算法的运行时间。最后，对实例进行了仿真测试，并与其他的算法进行了比较，实验结果表明该方法能有效地求解动态需求VRP。然而，动态VRP的研究还包括车辆的动态性和路网的动态性，如何综合考虑多种动态因素有待于进一步研究。

［1］DANTZIG G B，RAMSER J H．The truck dispatching problem ［J］．Management Science，1959，4（6）：80－91．

［2］IRNICH S．A multi－depot pickup and delivery problem with a single hub and heterogeneous vehicles［J］．European Journal of Operational Research，2000，122（2）：310－328．

［3］LI Jun，GUO Yaohuang．Theory and methods for vehicle scheduling on logistics distribution［M］．Beijing：China Supplies Press，2011（in Chinese）．［李 军，郭耀煌．物流配送车辆优化调度理论与方法［M］．北京：中国物资出版社，2001．］

［4］LIU Ran，JIANG Zhibin，CHEN Feng，et al．Full－load multidepot collaborative transportation problem：models and algo－rithms［J］．Journal of Shanghai Jiaotong University，2009，43（3）：455－459（in Chinese）．［刘 冉，江志斌，陈 峰，等．多车场满载协同运输问题模型与算法［J］．上海交通大学学报，2009，43（3）：455－459．］

［5］MA Jianhua，FANG Yong，YUAN Jie．Mutation ant colony algorithm for multiple－depot multiple－types vehicle routing problems with shortesr finish time［J］．Systems Engineering—Theory ＆Practice，2011，31（8）：1508－1516（in Chinese）．［马建华，房 勇，袁 杰．多车场多车型最快完成车辆路径问题的变异蚁群算法［J］．系统工程理论与实践，2011，31（8）：1508－1516．］

［6］YU Bin，YANG Zhongzhen，XIE Jingxin．A parallel improved ant colony optimization for multi－depot vehicle routing problem［J］．Journal of the Operational Research Society，2011，62（1）：183－188．

［7］DAMON G，BRUCE G，EDWARD W．The multi－depot split delivery vehicle routing problem：an integer programmingbased heuristic，new test problems，and computational results［J］．Computers and Industrial Engineering，2011，61（3）：794－804．

［8］LI Yanhui，LIU Xiang．Modeling and its ant colony algorithm for multi－depot open vehicle routing problem with replenishment on the way［J］．Computer Integrated Manufacturing Systems，2008，14（3）：260－265（in Chinese）．［李延辉，刘 向．沿途补货的多车场开放式车辆路径问题及蚁群算法［J］．计算机集成制造系统，2008，14（3）：260－265．］

［9］HANSHAR F T，OMBUKI－BERMAN B M．Dynamic vehicle routing using genetic algorithms ［J］．Applied Intelligence，2007，27（1）：89－99．

［10］WEN Min，CORDEAU J F，LAPORTE G，et al．The dynamic multi－period vehicle routing problem［J］．Computers ＆Operations Research，2010，37（9）：1615－1623．

［11］WANG Jiangqing，ZHU Rongbo．Efficient intelligent optimized algorithm for dynamic vehicle routing problem［J］．Journal of Software，2011，6（11）：2201－2208．

［12］HONG Lianxi．An improved LNS algorithm for real－time vehicle routing problem with time windows［J］．Computers ＆Operations Research，2012，39（2）：151－163．

［13］BERBEGLIA G，CORDEAU J F，LAPORTE G．Dynamic pickup and delivery problems［J］．European Journal of Operational Research，2010，202（1）：8－15．

［14］HAN K H，KIM J H．Quantum－inspired evolutionary algorithm for a class of combinatorial optimization ［J］．IEEE Transactions on Evolutionary Computation，2002，6（6）：580－593．

［15］ZHANG Jingling，ZHAO Yanwei，WANG Haiyan，et al．Modeling and algorithms for a dynamic multi－vehicle routing problem with customers'dynamic requests［J］．Computer Integrated Manufacturing Systems，2010，16（3）：543－555（in Chinese）．［张景玲，赵燕伟，王海燕，等．多车型动态需求车辆路径问题建模及优化［J］．计算机集成制造系统，2010，16（3）：543－555．］

［16］ZHANG Jingling，ZHAO Yanwei，PENG Dianjun，et al．A hybrid quantum－inspired evolutionary algorithm for capacitated vehicle routing problem ［C］／／Proceedings of Advanced Intelligent Computing Theories and Applications．Berlin，Germany：Springer－Verlag，2008，5226：31－38．