价格弹性需求下基于最小订购量的契约及供应链收益分析

丁 平，祁玉青，闵 杰

（1．合肥工业大学 管理学院，安徽 合肥 230009；2．中国科学技术大学 管理学院，安徽 合肥 230026；3．安徽建筑大学 数理系，安徽 合肥 230022）

0 引言

在实际的供应链管理中，核心企业的大部分经营利润往往是由少数大客户（指每次订购数量大或一时间段内总订购量大的客户）贡献的［1］。大量小客户（约占客户总数的70%～80%）占用企业的大量资源（如营销、配送、售后服务等资源），但是对利润的贡献却有限。为了降低成本、提高经营效率，很多企业按订购数量的不同对其客户进行等级划分，然后对不同等级的客户采取不同的服务方式。例如，对大客户提供更优惠的价格折扣，为大客户提供送货上门、免费培训服务等，其主要目的是激励大客户。与常规的大客户激励方法不同，还有一些企业通过设置最小订购量的要求来排除部分订购数量太小的客户，但其目的仍然是为了降低成本和提高经营效率。例如，Sport Obermeyer公司在中国大陆和香港地区的代工工厂，分别设置有1 200套和600套滑雪服的单次最低代工数量要求［2］；Kodak公司对其生产的35mm和16mm等型号的胶片也设置有最低购买数量的要求［3］。

最小订购量契约是供应链中常用的协调策略之一，它是指产品供应方（制造商）与其采购方（销售商）约定订购量的下限，即销售商如果向该制造商采购，则每次（或一段时间内）的订购量必须不少于预先约定或公布的数量。目前，与最小订购量有关的研究文献大致可以分为两类。第一类文献假定制造商对销售商的每次采购数量设置最小量要求。例如，Fisher等［4］研究了制造商设定最小订购量要求后，满足两个周期相关需求的生产计划决策问题［4］；Robb等［5］建立了给定最小订购量要求下周期性盘点的销售商库存决策模型，并且通过仿真实验分析比较了各种库存策略对收益的影响；Porras等［6］研究了在给定最小订购量要求下，销售商面对确定性需求时的多产品联合采购问题；Zhao等［7］证明了给定最小订购量要求下，销售商单产品周期性盘点库存问题的最优策略结构不具有简单形式；Zhou等［8］通过数值实验证明，在给定最小订购量要求下，销售商面对随机性需求、库存采取周期性盘点方式时，采取（s，t）订购策略的结果要优于（s，S）策略并且接近理论上的最优策略。第二类文献主要考虑制造商对销售商一段时间内的总订购量设定最小量要求。例如，Bassok等［9］研究了给定最小总订购量要求下，销售商面对不确定性需求时的单产品周期性订购策略问题；Chen等［10］在文献［9］的基础上进一步研究了给定最小总订购量要求下，销售商面对非平稳需求、产品批发单价变化时的库存决策问题；Kiesmuller等［11］在随机需求环境下讨论了单物品定期订货问题，且在每次订货时都要使用最小订购量契约；Okhrin I等［12］基于最小订购量研究了一个单物品的订货批量问题，并提出了O（T3）的精确算法；文献［13－16］也针对供应链协调的契约策略进行研究，得到了一些有意义的结论。

但是已有相关研究都侧重于研究给定最小订购量契约下，契约某一方的生产计划决策或库存决策问题，而对最小订购量契约的应用依据和设置方法问题的研究较少。制造商设定最小订购量的目的是要改变销售商的订购策略，限制其小批量的频繁订购；而销售商订购策略的改变又会反过来影响制造商的生产决策。因此，最小订购量契约的设定应当是在供应链上下游企业之间互动的过程中形成的。与现有文献将最小订购量当作外生变量不同，本文以一个制造商和若干销售商组成的两级供应链为背景，研究在供应链上下游企业互动过程中，基于价格弹性需求，研究制造商应当如何设置最小订购量契约，以及所设置的最小订购量契约对供应链收益影响的变化范围。

1 符号和假设

考虑由一个制造商和N个销售商组成的两级供应链，N个销售商以批发价格w从制造商处采购同一种产品。本文考虑最小订购量要求发生在销售商每次采购决策时的情况，即制造商规定：销售商每次（若订购）的订购量必须不少于M数量。在制造商设置最小订购量契约后，每个销售商都面临两种选择：接受该契约（即每次订购数量都不少于M）和拒绝该契约（即放弃订购）。因此，对于本文研究的问题，制造商和销售商之间是一种典型的以制造商为主导者（leader）的Stackelberg博弈，具体博弈过程可以描述为：①各个销售商在制造商提出的最小订购量要求下，采取最优策略，使得自己的收益最大化；②制造商在考虑各个销售商反应的基础上，设定最优最小订购量，使得自身的收益最大化。制造商单位成本c、批发单价w都是常数。

本文主要考虑制造商和销售商之间的博弈关系，针对销售商的市场需求作以下两个假设：

假设1 每个销售商的市场需求是相互独立的，即市场需求只与自身价格相关。

假设2 每个销售商的市场需求是价格的确定性函数，并且价格相同时的需求价格弹性相同。

假设1要求销售商的市场需求是独立的，即忽略销售商之间的价格竞争关系，这种情形在现实中大量存在。例如，许多制造商对其销售商实行区域独家代理机制，以防止互相之间的价格竞争。此外，电信、煤炭等垄断性商品也符合假设1的特征，其中最小订购量契约的使用是常见的现象。一般当顾客在销售商之间切换的成本比较高时，可以近似认为假设1成立。

需求价格弹性是指需求量对价格变动的反应程度，即需求量变化的百分比除以价格变化的百分比。通常认为影响需求价格弹性的因素［17］主要有商品的必需程度、可替代性、类别大小、消费者收入因素和时间的长短。因为本文考虑同一种产品，所以假设2意味着各个销售商面对的消费者是同质的，即不同销售商面对的消费者的收入结构基本相同。

根据假设1和假设2，可以得到销售商需求函数的一般形式。

定理1 当满足假设1和假设2时，销售商的需求函数可以写成Di＝Siq（p）（i＝1，2，…，N）的形式。其中：Di为销售商i的市场需求量，p为零售价格，q（p）为p的函数，Si为与销售商i有关的常数且Si≥1。

证明 见附录。

从销售商的需求函数 Di＝Siq（p）（i＝1，2，…，N）可以看出，当所有销售商的价格都相同时，Si越大的销售商的需求量也越大。因此，Si可以被看作销售商i固有需求规模的大小。

定义1 设N个销售商的需求函数Di＝Siq（p）（i＝1，2，…，N），其中q（p）是p的减函数，定义Si为销售商i的需求规模系数，简称规模系数。

2 最小订购量契约下销售商的策略

由于制造商和销售商之间是Stackelberg博弈关系，首先需要考虑各个销售商在最小订购量契约下的反应，即各个销售商的最优零售价格和最优订购量。由于需求量是价格的确定性函数，在订购量不为0时，销售商i的订购量Qi等于其市场需求量Di。假设最小订购量要求为M，根据利润最大化原则，在订购量不为0时，销售商i的目标函数可以表示为

而当销售商i的订购量为0时，其利润也为0。因此，综合订购与不订购两种可能，销售商i的目标函数可以表示为

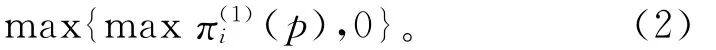
Ozelkan［18］，Lau［19］等证明了对于常见的确定性需求函数，如线性（linear）函数、分对数（logit）函数、等弹性（iso－elastic）函数和对数（logarithmic）函数，在无最小订购量要求时，销售商的收益函数都是“强单峰的”。因此，在本文的分析中，不假定q（p）的具体形式，而是假定在无最小订购量要求的情况（M＝0）下，销售商i的收益函数是满足强单峰性的。

根据销售商i的目标函数（2），可得在最小订购量为M时，销售商i的最优零售价格。

定理2 设最小订购量为M，销售商i的需求函数Di＝Siq（p），则销售商i的最优零售价格

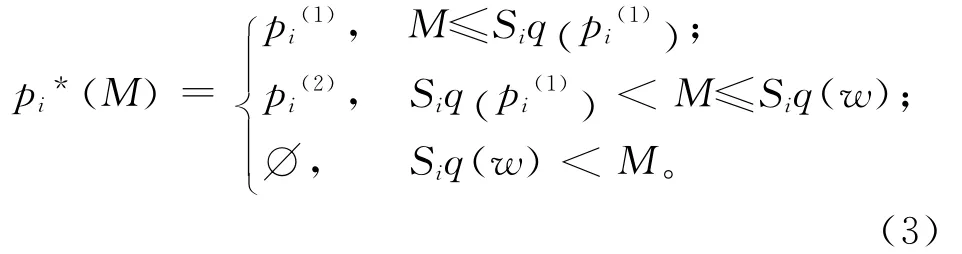
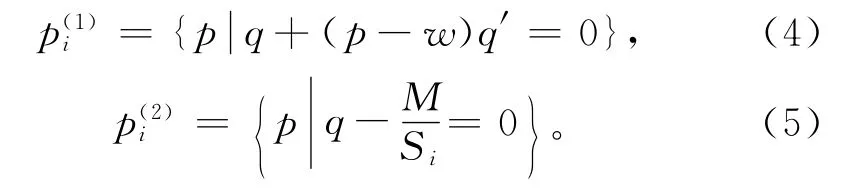
符号∅表示没有值，由于此时销售商i不订购，也就没有所谓的最优零售价格。

证明 见附录。

定理3 设最小订购量为M，销售商i的需求函数Di＝Siq（p），则销售商i的最优订购量

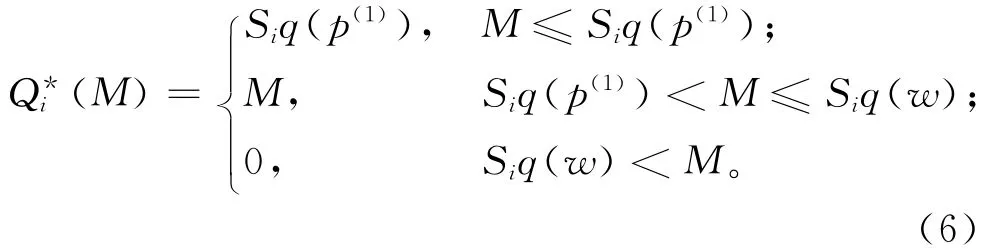
证明 见附录。

3 最小订购量契约的设计

因为制造商是博弈的主导者，所以制造商在考虑销售商反应的基础上，设定最优最小订购量使其自身收益最大化。因此，基于销售商i在最小订购量为M 时的最优订购量（定理3），可以得到制造商的目标函数

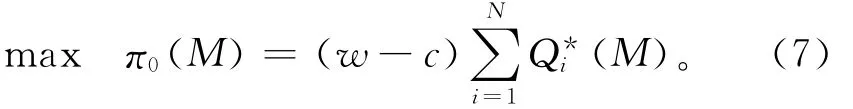
因为制造商的单位成本c和批发单价w都是常数，所以式（7）等价于

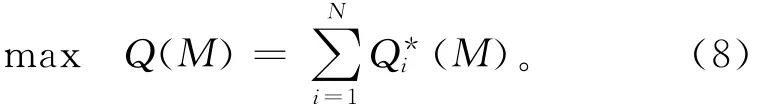
寻找制造商的最优策略（最优最小订购量），就是求满足上述优化问题的最优解M＊。首先给出一个引理。

引理1 设M1≤M2≤Siq（w），则成立。

引理1表明，在保证销售商i订购量不为0时（即最小订购量要求小于等于Siq（w）），最小订购量要求越高，销售商i的订购量就越多。根据引理1，可以证明定理4。

定理4 设M＊是式（6）的最优解，则M＊∈｛S1q（w），S2q（w），…，SNq（w）｝。

证明 见附录。

定理4表明，模型（6）的最优解只可能在S1q（w），S2q（w），…，SNq（w）这 N 个点中取值，因此可以直接对这N个点进行枚举，求得最优解。

算法1

初始化。令Q＊＝0，M＊＝0，n＝1，计算q（w），p（1）和q（p（1））。

步骤1 令 M ＝Snq（w），带入式（3）计算，然后汇总计算

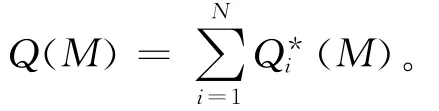
步骤2 若Q（M）＞Q＊，则令Q＊＝Q（M），M＊＝M。

步骤3 若n＜N，则令n＝n＋1，返回步骤1。

步骤4 输出M＊和Q＊，算法结束。

整个算法需要从M＝S1q（w）到M＝SNq（w）共执行N次。在每次执行过程中，需要计算显然算法1的时间复杂度为O（N2）。

4 最小订购量契约对供应链收益的影响

对于供应链中的各方企业来说，它最关心的是新契约机制带来的收益变化情况。为了分析供应链的收益变化，首先对销售商的下标序号进行调整。不失一般性，假设销售商是按其规模系数Si（i＝1，2，…，N）从小到大的顺序编号，即S1＜S2＜…＜SN。根据定理4，最优最小订购量（记 M＊）是S1q（w），S2q（w），…，SNq（w）这 N 个点中的一个。假设M＊＝SKq（w），即

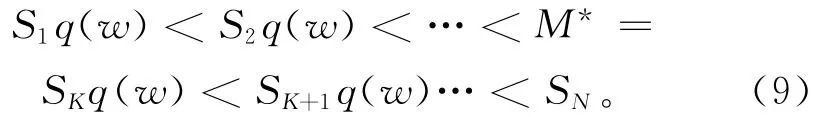
根据定理3可知，在最小订购量为M＊时，销售商1～销售商K－1都不订购，销售商K～销售商N都订购至少M＊。

由 于 SKq（p（1）） ＜ SKq（w），SKq（p（1）） ＜SK＋1q（p（1））＜ … ＜ SNq（p（1）），根 据 定 理 3 可 知，如果：

（1）存在ST＋1q（p（1））≥SKq（w），则销售商K～销售商T的订购量为M＊；销售商T＋1～销售商N的订购量为Siq（p（1）），i＝T＋1，…，N。

（2）SNq（p（1））＜SKq（w），则销售商K ～ 销售商N的订购量都为M＊。

4．1 对制造商收益的影响

根据上述分析，当M＊＝SKq（w）时，制造商的收益可以表示为

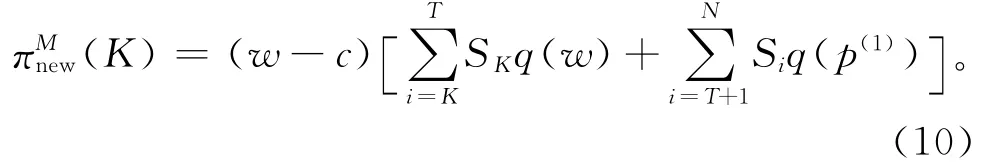
在不采取最小订购量契约时，销售商i的订购量为Siq（p（1））（i＝1，…，N），此时制造商的收益可以表示为

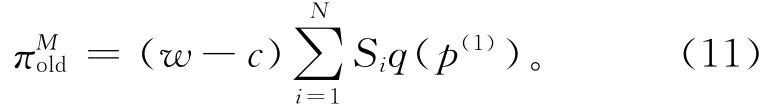
根据制造商的收益函数，可以得到制造商收益变化的一个上界。

证明 见附录。

4．2 对整个供应链收益的影响

因为制造商是供应链的主导者，所以与不采取最小订购量契约相比，制造商的收益必定是增加或至少不变的（因为制造商可以选择最小订购量为0）。对于销售商来说，制造商采取最小订购量契约后，其收益必定是减少或至多不变的（因为有约束条件（最小订购量约束）的最优化问题的最优解必定不优于其无约束时的最优解）。一个自然的问题是，在采取最小订购量契约后，整个供应链的收益（制造商的收益＋N个销售商的收益）如何变化。

根据定理2和定理3，以及S1，S2，…，SN的递增关系可知，当M＊＝SKq（w）时，整个供应链的收益可以表示为

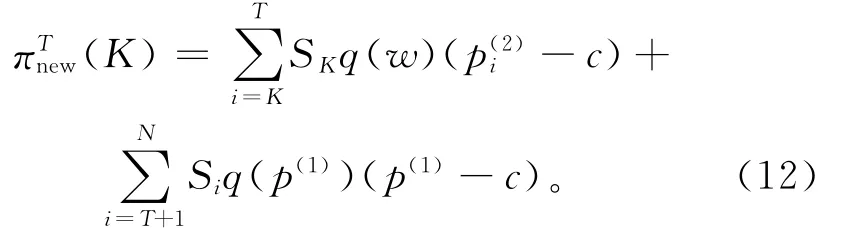
在不采取最小订购量契约时，销售商i的订购量为Siq（p（1））（i＝1，…，N），零售价格为p（1），因此此时整个供应链的收益可以表示为

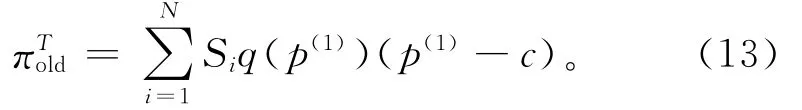
证明 见附录。

5 数值分析

为了说明模型的应用，以两种最常用的确定性需求函数——线性函数和等弹性函数为例，通过数值方法分析最小订购量契约对供应链收益的影响。在计算中，取销售商数目N＝100。为了体现实际情况下销售商规模大小的随机性，以1 000个截尾正态分布随机数代表销售商的规模系数，其中均值μ＝500，标准差σ＝100；制造商单位成本c＝5，批发价格w＝8。

5．1 线性需求函数时的情形

对于线性需求函数q（p）＝a－bp（a，b＞0），使b从0．025～0．5变化，变化步长为0．025；a从10．5～20变化，变化步长为0．5。图1所示为线性需求函数下，采取最小订购量契约前后制造商的收益情况。

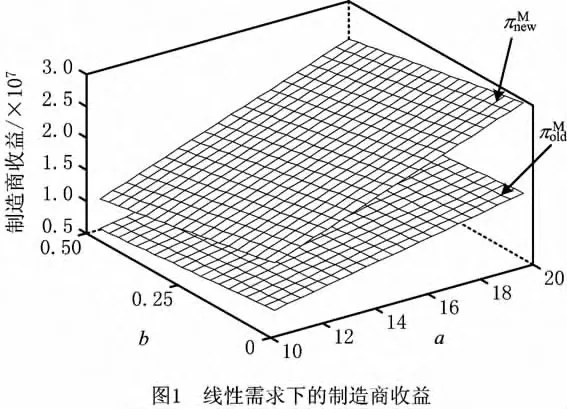
从图1可以看出，采取最小订购量契约后，制造商的收益要高于不采取最小订购量契约时的收益。当a增加或者b减少时，采取最小订购量契约前后制造商的收益都是增加的。

根据定理5，采取最小订购量契约后，制造商的收益最多增加

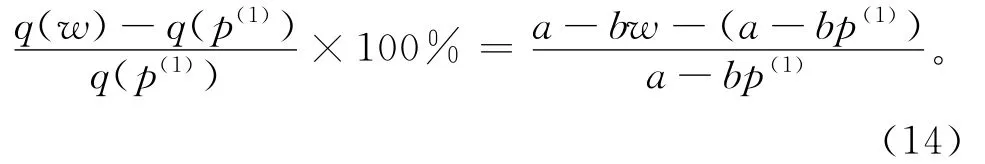
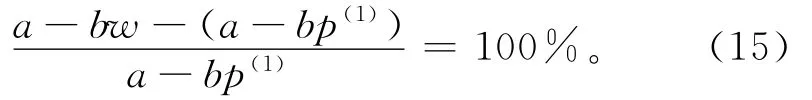
因此，在线性需求函数情况下，无论a和b如何取值，采取最小订购量契约后，制造商的收益最多增加100%。

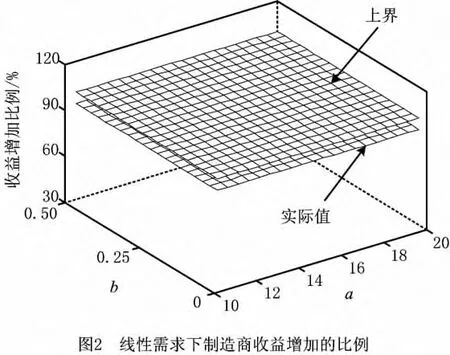
图2所示为与不采取最小订购量契约相比，采取最小订购量契约后制造商实际收益增加的比例与本文给出的理论上界值。从图2可以看出，在线性需求函数情况下，本文给出的上界较好地反映了制造商收益变化的趋势。在具体计算结果中，实际增加的比例大约在92．5%左右，因此本文给出的上界（100%）比实际值大约高7．5%左右（最大高7．8%，最小高7．2%）。

图3所示为线性需求函数下，采取最小订购量契约前后，整个供应链的收益（制造商收益＋N个销售商收益）情况。从图3可以看出，采取最小订购量契约后，整个供应链的收益低于不采取最小订购量契约时的收益。当a增加或者b减少时，采取最小订购量契约前后整个供应链的收益都是增加的。

综合上述分析，可以得到如下性质。

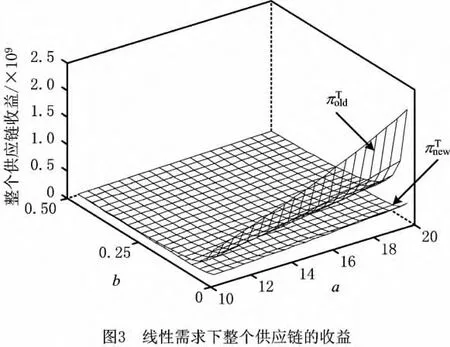
性质1 在销售商需求是线性函数时，制造商采取最小订购量契约是在损害整个供应链收益的情况下，使自身的收益增加；相比于不采取最小订购量契约，制造商收益的增加不会超过100%。这是因为制造商和销售商之间是Stackelberg博弈关系，而制造商在博弈中处于主导地位，所以制造的获益显然是优先的。

5．2 等弹性需求函数时的情形

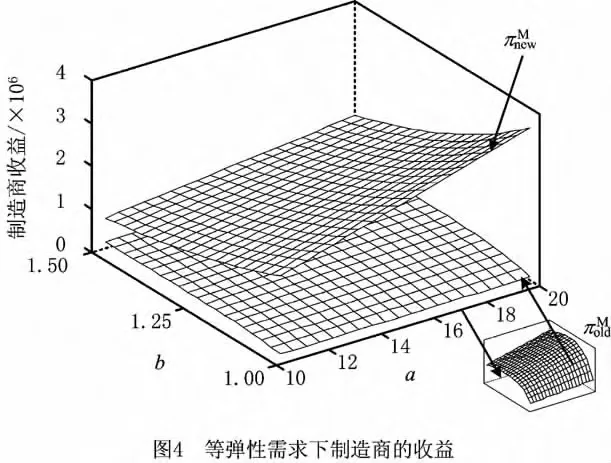
对于等弹性需求函数q（p）＝ap－b（a＞0，b＞1），使b从1．025～1．5变化，变化步长为0．025；a从10．5～20变化，变化步长为0．5。图4所示为等弹性需求函数下，采取最小订购量契约前后制造商的收益。

从图4可以看出，采取最小订购量契约后，制造商的收益高于不采取最小订购量契约时的收益。当a增加时，采取最小订购量契约前后制造商的收益都是增加的。但是与线性需求函数不同，在不采取最小订购量契约时，当销售商的需求价格弹性系数b增加时，制造商的收益先增加后减少。这表明不采取最小订购量契约时，随着b的变化，销售商的总订购量存在着一个极大值（批发价格和制造商成本是固定的）。

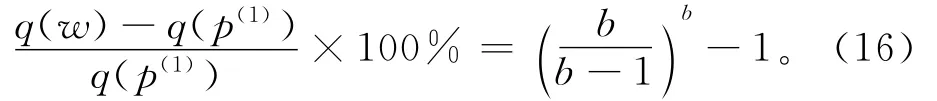
显然上式随b的增加逐渐减少并趋向于（e－1）≈172%。

图5所示为与不采取最小订购量契约相比，采取最小订购量契约后制造商实际的收益增加比例与本文给出的理论上界值。从图5可以看出，本文给出的上界较好地反映了制造商收益变化的趋势。在具体计算结果中，本文给出的上界比实际收益增加的比例平均高4．5%左右（最大高4．9%，最小高3．9%）。

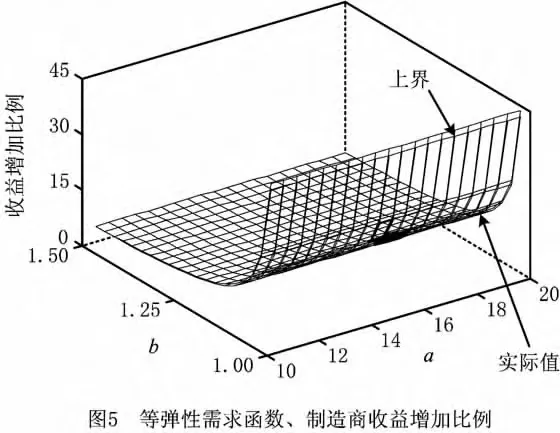
图6所示为等弹性需求函数下，采取最小订购量契约前后整个供应链的收益情况。从图6可以看出，采取最小订购量契约后，整个供应链的收益低于不采取最小订购量契约时的收益。

综合上述分析，可以得到如下性质：

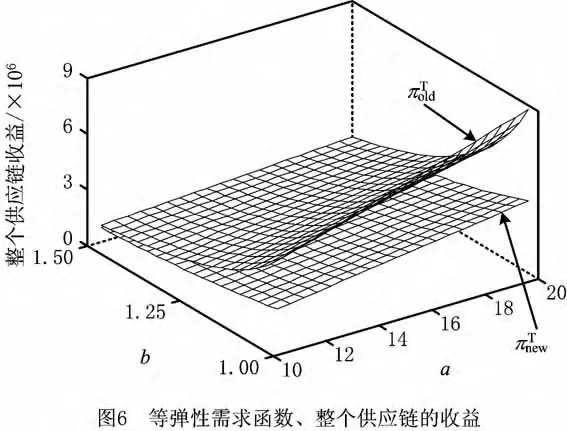
性质2 在销售商需求是等弹性函数时，制造商采取最小订购量契约是在损害整个供应链利益的情况下，使自身收益增加；与不采取最小订购量契约相比，制造商收益增加的比例随着销售商的需求价格弹性系数b的增加而减少，并且随着弹性系数b的增加，其上界最终不会超过172%，这也是由制造商在博弈中占主导地位所导致的。

6 结束语

本文以由一个制造商和多个销售商组成的两级供应链为背景，基于价格弹性需求，研究了在以制造商为主导者的Stackelberg博弈机制下，最小订购量的设定方法及其对供应链造成的影响。主要工作概括如下：

（1）证明了在最小订购量契约下，销售商的订购策略为一种分段函数的形式。

（2）提出了一种精确求解最优最小订购量、时间复杂度为O（N2）的算法。

（3）找到了与不采取最小订购量契约相比，在最小订购量契约下制造商收益变化的上界与整个供应链收益变化的下界。

（4）通过数值实验证明，在以制造商为主导者的Stackelberg博弈机制下，制造商采取最小订购量契约可以使自身收益增加，但是会使整个供应链收益减少。与不采取最小订购量契约相比，在线性需求函数下，制造商收益增加的比例不会超过100%；在等弹性需求函数下，制造商收益增加的比例随着弹性系数b的增加而减少，并且随着弹性系数b的增加，其上界最终不会超过172%。

本文考虑需求函数是确定性的形式，今后可以进一步考虑不确定需求的形式。本文将制造商的批发价格看作是外生变量，还可以进一步考虑最小订购量和批发价格同时为制造商决策变量时的供应链协调问题等。

［1］REED W J．The pareto，zipf and other power laws［J］．Economics Letters，2001，74（1）：15－19．

［2］HAMMOND J H，RAMAN A．Sport Obermeyer，Ltd．［EB／OL］．（2006－08－15）［2011－11－13］．http：／／www．log．wi．tum．de／fileadmin／w00bkn／www／GlobalSCS2012／VL＿6＿－＿08－05－2012＿－＿HBR＿Case．pdf．

［3］Kodak．Kodak motion picture products price catalog［EB／OL］．［2009－01－02］．http：／／motion．kodak．com／motion／uploadedFiles／QA＿MotionPictureCatalog＿March9＿2009．pdf．

［4］FISHER M，RAMAN A．Reducing the cost of demand uncertainty through accurate response to early sales［J］．Operations Research，1996，44（1）：87－99．

［5］ROBB D J，SILVER E A．Inventory management with periodic ordering and minimum order quantities［J］．Journal of Operational Research Society，1998，49（10）：1085－1094．

［6］PORRAS E，DEKKER R．An efficient optimal solution method for the joint replenishment problem with minimum order quantities［J］．European Journal of Operational Research，2006，174（3）：1595－1615．

［7］ZHAO Y，KATEHAKIS M N．On the structure of optimal ordering policies for stochastic inventory systems with minimum order quantity［J］．Probability in the Engineering and Informational Sciences，2006，20（2）：257－270．

［8］ZHOU B，ZHAO Y，KATEHAKIS M N．Effective control policies for stochastic inventory systems with a minimum order quantity and linear costs［J］．International Journal of Production Economics，2007，106（2）：523－531．

［9］BASSOK Y，ANUPINDI R．Analysis of supply contracts with total minimum commitment［J］．IIE Transactions，1997，29（5）：373－381．

［10］CHEN F Y，KRASS D．Analysis of supply contracts with minimum total order quantity commitments and non－stationary demands［J］．European Journal of Operational Research，2001，131（2）：309－323．

［11］KIESMULLER G P，DE KOK A G，DABIA S．Single item inventory control under periodic review and a minimum order quantity［J］．International Journal of Production Economics，2011，133（1）：280－285．

［12］OKHRIN I，RICHTER K．An O（T3）algorithm for the capacitated lot sizing problem with minimum order quantities［J］．European Journal of Operational Research，2011，211（3）：507－514．

［13］HUA Guowei，LI Jian，TIAN Xin，et al．Optimal order strategy with free shipping option ［J］．Systems Engineering—Theory ＆ Practice，2010，30（3）：506－512（in Chinese）．［华国伟，李 健，田 歆，等．带有免费送货选择的最优订货策略［J］．系统工程理论与实践，2010，30（3）：506－512．］

［14］XU Qi．Jointly contract of buy back and pricing flexible for supply chain coordination under price changing on demand［J］．Forecasting，2012，30（3）：25－29（in Chinese）．［徐 琪．价格相关需求下基于回购与价格弹性联合契约的供应链协调［J］．预测，2012，30（3）：25－29．］

［15］LIAO Li，WU Yaohua，SUN Guohua．Contract coordination for a two－stage supply chain with random yield［J］．Computer Integrated Manufacturing Systems，2010，16（8）：1733－1741（in Chinese）．［廖 莉，吴耀华，孙国华．随机产量下的二级供应链契约协调［J］．计算机集成制造系统，2010，16（8）：1733－1741．］

［16］QI Ershi，YANG Daojian，LIU Liang．Supply chain two－part tariff based on strategic customer behavior［J］．Computer In－tegrated Manufacturing Systems，2010，16（4）：828－833（in Chinese）．［齐二石，杨道箭，刘 亮．基于顾客战略行为的供应链两部定价契约［J］．计算机集成制造系统，2010，16（4）：828－833．］

［17］HUANG Yajun．Microeconomics［M］．Beijing：Higher Education Press，2005（in Chinese）．［黄亚钧．微观经济学［M］．北京：高等教育出版社，2005．］

［18］OZELKAN E C，CAKANYILDIRIM M．Reverse bullwhip effect in pricing［J］．European Journal of Operational Research，2007，192（1）：302－312．

［19］LAU A H L，LAU H S．Effects of a demand curve's shape on the optimal solutions of a multi－echelon inventory／pricing model［J］．European Journal of Operational Research，2003，147（3）：530－548．