一种自动的非封闭曲面三维重建方法

温佩芝，宁如花，吴晓军，黄锦芳

（1．桂林电子科技大学 计算机科学与工程学院，广西 桂林 541004；2．哈尔滨工业大学 深圳研究生院机电工程与自动化学院，广东 深圳 518055）

0 引言

随着三维扫描技术的日益发展，三维点云模型已大量应用于逆向工程［1－2］、计算机辅助设计（Computer Aided Design，CAD）［3］、机械制造、医学影像、虚拟现实和动漫等领域。但实际扫描获得的三维点云数目较为庞大、边缘模糊、模型的拓扑结构不清晰，给曲面重建带来了很大的困难，尤其是非封闭曲面的三维重建，目前仍是计算机图形学领域研究的一个难点问题。

在三维点云模型曲面重建方法中，已有多种曲面模型表达形式，比较常用的是隐式函数表达形式。隐式函数方法大致分为全局方法和局部方法。全局拟合法通常定义隐式函数为以样本点为中心的径向基函数（Radial Basis Function，RBF）的加权和［4－6］，但易产生平凡解，无法进行重建，同时因其全局性对数据的要求是完整的、封闭的，对非封闭的模型往往不能重建出模型的曲面；局部拟合方案是利用八叉树将散乱数据点集分割成多个小区域，在每个子区域中应用分段二次曲面函数进行拟合，然后用MPU（multi－level partition of unity）函数将各个子区域函数加权求和拼接出全局函数［7］，该方法具有运算速度快的优势，但不具备抗噪性，要求点云模型不能含有噪声。然而，采用MPU算法对非封闭的模型曲面进行重建时，在非封闭的模型边缘易产生大量不规则且不合理的伪面片。

当前曲面重建技术中的新热点——泊松算法［8］结合了全局和局部拟合方法的优点。因为该算法是全局的，所以在形成邻近区域和调整权重时不涉及启发式的决策，但是其基函数与周围空间相关而不是与数据点相关，是局部的，因此泊松重建算法具有多分辨率结构，从而产生一个稀疏的矩阵系统，加快了计算的速度；泊松算法还能很好地捕捉曲面的细节，重建精度高于其他隐式算法。然而，泊松曲面重建算法过程不引入与模型形态相关的信息，故泊松重建的模型是水密（watertight）的，对不封闭的点云模型，它会自动重建出封闭的曲面，因此非封闭的模型曲面重建不能直接应用泊松算法。

针对上述问题，受二维图像分割大律法（OTSU）阈值方法［9］的启示，本文提出一种基于曲面三角面片周长的阈值分割方法，引入泊松算法实现了三维非封闭曲面的准确重建。首先，利用泊松算法进行三维曲面重建，然后根据生成曲面的小三角面片的周长大小分布概率，从生成的三角面片中选出比对的样本点，计算样本点与原始输入点的距离，根据原始点到伪平面三角点的距离明显大于原始点到模型曲面三角点距离的特性，将三角点分为伪平面三角点和模型曲面三角点两类，计算原始输入点到模型曲面三角点的平均最大距离，将其设为分割阈值T，保留距离小于T的点而去除距离大于T的点，即可分割出非封闭的模型曲面。实验结果表明，该算法能准确有效地去除伪封闭曲面而不影响原生成曲面的精度，算法复杂度低、时间效率高、鲁棒性强，从而解决了非封闭模型曲面三维重建的技术难题，拓展了泊松算法的实际应用范围。

1 泊松重建方法

1．1 泊松数学模型

S是输入三维模型的点集，其中的一个样本s∈S，每个样本包含一个点s．p和一个内法线s．N，给定一个三维实体M，其边界为∂M，用χM表示M 的指示函数，即曲面内的点定义为1，曲面外的点为0，N∂M（p）表示p点（p∈∂M）的向内曲面法线（q）为

给定一个样本点集S和最大深度D，定义八叉树O为每个样本点都落在深度为D的叶子节点上的最小八叉树。

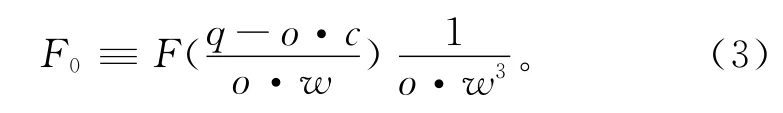
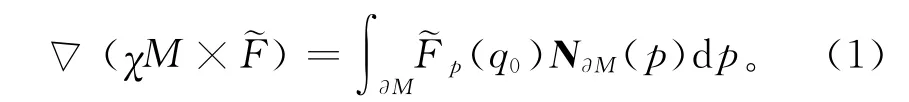
把物体表面∂M分割为不同的小面片Ps⊂∂M，可以根据样本点s．p的值和小面片面积的乘积近似计算小面片Ps上的积分［8］

式中o·c和o·w分别是节点o的中心和宽度。

为提高效率，本文用一个简化的函数来近似单位方差滤波器，使得计算的散度和拉普拉斯算子都是稀疏的，因此设F为一个盒滤波器的n阶卷积［8］，

为了达到子节点的精度，避免采用叶子节点的中心近似为采样点的位置，取而代之的是使用三次线性插值法分配样本点到八个最邻近的节点，这样可以定义曲面函数梯度场的近似值

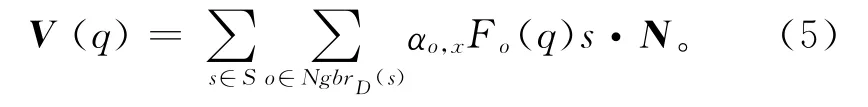
式中：NgbrD（s）为最邻近s·p的8个深度为D 的节点，｛αo，s｝为三次线性插值的权。

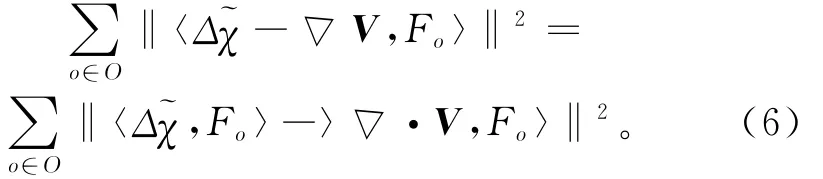
给定｜O｜维向量v，其第o个坐标为vo＝〈▽，V，Fo〉，求解的目标是解使得▽在空间FO，F上的投影尽可能接近▽·V的投影。对于每个o和o′，L在（o，o′）处的元素设为

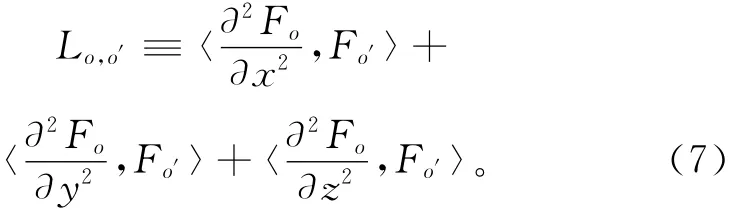
1．2 重建结果比较

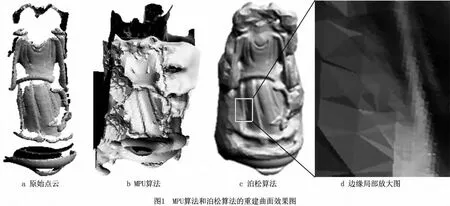
图1所示为MPU算法和泊松算法对图1a模型重建曲面的效果。图1a是不封闭的原始点云数据模型；图1b是MPU算法重建的模型曲面，在非封闭模型曲面的边界处，算法生成的曲面不规则且存在较多不合理的伪曲面；图1c为泊松算法重建的效果图。由图1可见，泊松算法重建的曲面效果比MPU重建效果好，曲面结构特征符合原始模型，所生成的曲面较光顺。但从实验结果也可以明显看出，对于原非封闭的曲面模型，泊松算法重建自动生成了封闭的伪曲面，这给实际应用带来了诸多不便。

从上述实验结果可以看出，对于非封闭的模型，图1b的MPU算法重构的曲面不能正确表达原始模型的特征，边缘处产生较多不规则的伪曲面。图1c中泊松重建的曲面模型，重建曲面光顺且能很好地反映模型的特征，但只能重建出watertight的封闭曲面。目前在实际应用中，大多采用人工手动割除重建生成的多余的伪曲面，这不但需要操作人员具有较高的专业水平，而且很难确定准确的边缘，效率较低。对此，受二维图像阈值分割思想的启发，本文提出一种新的三维非封闭曲面重建自动阈值分割算法。

2 三维分割阈值计算

为了将非封闭曲面重建出现的伪封闭曲面分割出去，借鉴二维图像处理中OTSU阈值分割方法［5］的思想，OTSU算法是以图像的一维直方图为依据，将图像分成背景和目标两部分，以背景和目标之间的类间方差最大为阈值选取准则，此算法在二维图像处理中能取得很好的分割效果。但是，本文分割的对象是由三维点云模型重构的模型曲面，如何将二维图像的分割思想转换到三维模型空间，研究适用于三维模型的分割阈值算法，是本文研究的重点。以下为本算法的主要思想：

已知隐式曲面可视化是利用很多细小的三角面片去逼近实际模型表面，即重构出的模型曲面由大量的三角面片构成。假设构成三角面片的三个顶点为v1，v2和v3，称为三角点；三角面片的三边长度分别为e1，e2和e3，则三角面片周长L＝e1＋e2＋e3。

由图1d可见，泊松算法重建的封闭曲面，模型外三角面片的数目相对较少，构成伪封闭曲面的三角面片周长比模型曲面上的三角面片周长要大，但在模型边缘的曲面，三角面片面积逐渐增大、周长逐渐增加，并没有明显的边界区分，因此采用人工的方法很难准确地对生成的封闭曲面进行分割。

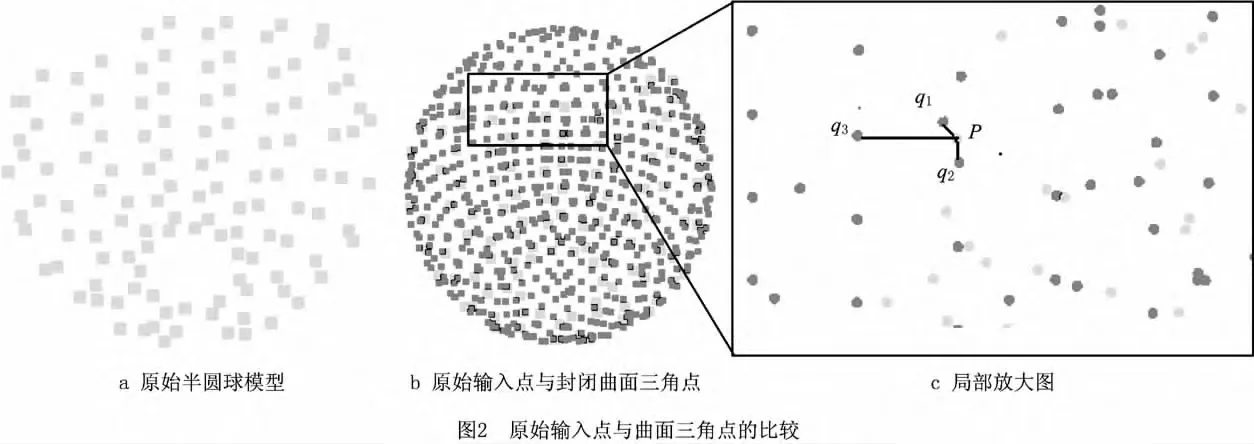
原始点云数据与重建曲面时生成的三角面片的三角点存在密切的关系。一般而言，三角点都落在原始输入点附近，如图2a所示的半圆球模型；泊松重建后得到封闭的圆球曲面，图2b中深色点为生成的封闭圆球曲面三角面片的三角点，浅色点为原始半圆球模型输入数据点，由图可知，模型曲面上的三角点分布在原始输入点附近，且与原始输入点距离较近，而伪平面三角点分布在原始模型输入点外侧，远离原始输入点；图2c所示为图2b中黑色方框放大后的点云分布情况，浅色点p为原始输入点，q1，q2和q3为三角点，其中q3为伪平面的三角点，q1和q2为模型曲面上的三角点，可见p点到q1和q2的距离明显比到q3的距离小。利用这一特性，根据重建曲面三角点的密度分布，求取原始输入点到模型曲面单位圆内三角点的平均最大距离，将其设定为分割阈值T，然后分别计算原始输入点与重建曲面三角点间的距离，将距离大于阈值T的三角点去掉，保留小于阈值T的三角点，从而准确地重建出非封闭模型曲面。

2．1 采集样本点

由上述分析可知，要找到分割阈值，必须将模型曲面上的三角点与原始输入点进行距离比较。但是如果将模型曲面上所有三角点与原始输入点进行比较，则计算量较大，为了减少内存消耗，采集模型曲面上的部分三角点作为比较的样本。由图2c可知，模型曲面的三角点基本上都落在原始输入点附近，而伪封闭曲面的三角点离原始输入点较远。因此，可以通过采集部分在模型曲面上的三角点作为比较的样本点。因为位于模型曲面上的三角面片周长较小，数目较多，出现相同周长的概率越大，所以可以通过计算生成三角面片的周长，按相同周长出现的概率大小采集样本点来计算阈值。

假设泊松算法进行模型重建时生成的三角面片的边的集合A＝a1i，a2i，a3i，i＝1，…，Q，Q 为重建模型上全部三角面片的个数。则每个三角面片的周长

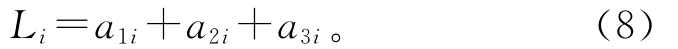
按以下步骤采集样本点：

步骤1 按像素的概念将每个周长Li同乘以一个倍数，扩大到整数L′i。

步骤2 将L′i的最小值标记为L′min、最大值标记为L′max，则三角面片周长的大小范围为［L′min，L′max］，其中周长为L′j的三角面片的总个数为μj，分布概率为

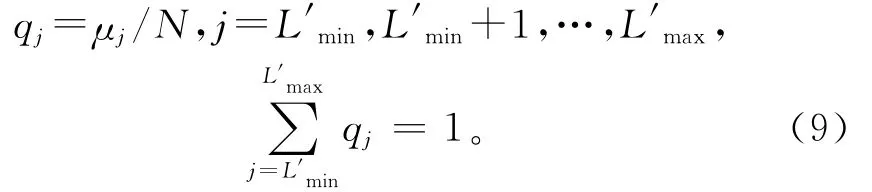
步骤3 将分布概率由大到小进行排列，选取前面分布概率大的g个周长L′i（i＝1，…，M）对应的三角面片为样本，每个周长对应3个三角点，则一共有M′＝3g个样本点，将样本点集合记为X＝｛xi｜i＝1，…，M′｝。实际计算时，可根据经验随机选取一个适当的g来采集样本点。

2．2 阈值计算

为了割除泊松算法对非封闭点云数据重建生成的伪封闭曲面，需要找到一个自适应阈值来自动保留非封闭曲面模型边界内的点，而除去模型边界外的点。首先计算以上获得的M′个样本点与原始输入点的距离，假设原始输入点的个数为k，则原始输入点的集合P＝｛p1，…，pk｝，对应法向量的集合V＝｛v1，…，vk｝，pi，vi∈R3，则每个样本点到原始输入点集的欧氏距离

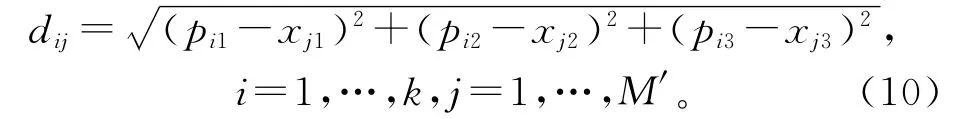
将dij按列固定，每列由小到大进行排列。设生成曲面模型对应的点云数目为k′，则生成曲面前后点云数目的比例

如果输入原始点云数据的密度为ρ（即以某点为中心的单位圆内点的数目），则生成新的点云密度为

取dij的第［ρ′］行，计算平均值

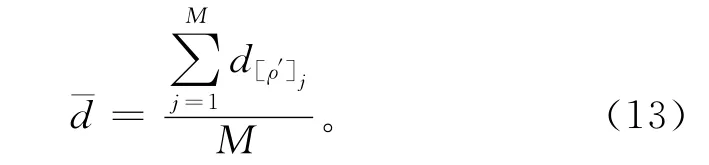
3 曲面分割

步骤1 设生成曲面的点云数据的集合P′＝｛p′1，…，p′N′｝，对应法向量的集合V′＝｛v′1，…，v′k′｝，遍历每个p′i，如果满足

则将p′i标记为1，即保留此点；如果不满足，则标记p′i为0，即为要割除的点。

步骤2 去除含有标记为0的三角点的三角面片，保留标记为1的三角点的三角面片，从而完成伪封闭曲面的割除，得到真实的非封闭模型曲面。

4 实验结果

在VC＋＋6．0和OpenGL环境中实现了上述算法，计算机硬件配置为PⅣ3．0GHz CPU，2．0 GB内存。对20组非封闭的点云模型进行泊松三维重建及分割实验。实验结果表明，使用本文算法对泊松三维重建生成的伪封闭曲面均能取得较好的分割效果，且算法鲁棒性强、稳定可靠。下面给出部分实验结果，其中模型的分割阈值如表1所示。

图3和图4所示为明显的不封闭模型。图3是马体模型的分割效果图，从图3a可以看出，原始点云是不封闭的模型，图3b是泊松算法自动重建出的模型封闭曲面，利用本文算法计算出分割阈值T＝0．16，可以很好地将封闭的曲面分割出来，分割结果准确，分割边缘光顺，如图3c所示。对图4的髋部非封闭模型，利用本算法也能准确有效地将封闭的伪曲面分割出去，如图4c所示。

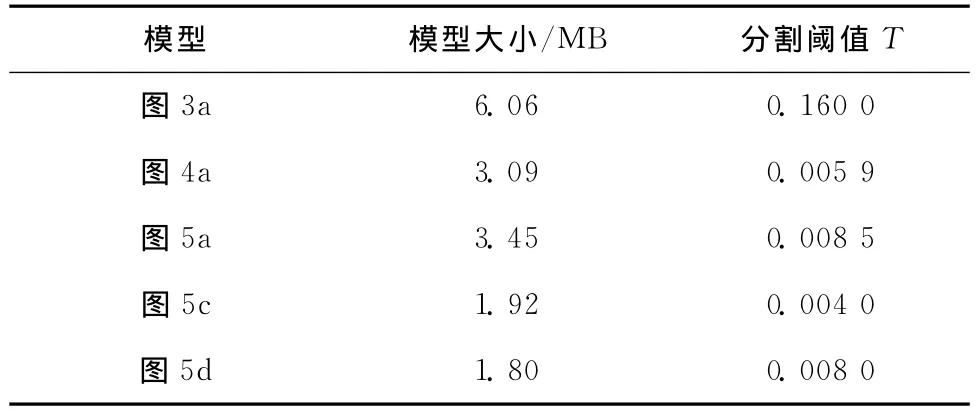
表1 模型分割阈值T

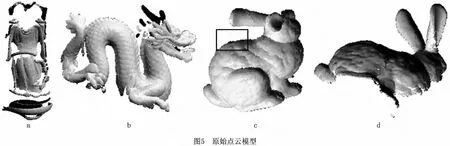
图3和图4是一组比较理想的扫描模型，使用本算法对模型进行分割能取得很好的效果。但在实际的三维模型采集中，采集的数据往往各式各样，为了说明本算法的稳健性，采用多组斯坦福大学采集的三维扫描数据［10］进行实验。本文给出三组数据的实验结果及对比分析，带有法向量的点云数据如图5所示，图5c和图5d为兔子模型多视角的显示效果。由图5可知，扫描的三维数据由实际数据采集，模型都是不封闭且边缘复杂不规则的，明显增加了分割的难度。图6所示为图5中点云模型的泊松重建曲面模型，由图可见，重建的模型都是封闭的。图7所示为本文分割算法计算获得的曲面模型，由图可知，使用本算法能很好地将封闭曲面分割出来，且都很好地还原了原始模型复杂不规则的边缘，对比图5c、图6c和图7c黑色方框内的曲面部分可知，本文算法能够能很好地分割出点云的边界，同时重建的曲面仍具有隐式曲面的特点，而且能够很好地还原模型的原始边界特征。通过大量实验结果对比分析可知，采用本文所提算法能够使绝大部分非封闭三维点云模型都能获得高质量的非封闭曲面模型，充分验证了本算法的稳健性。

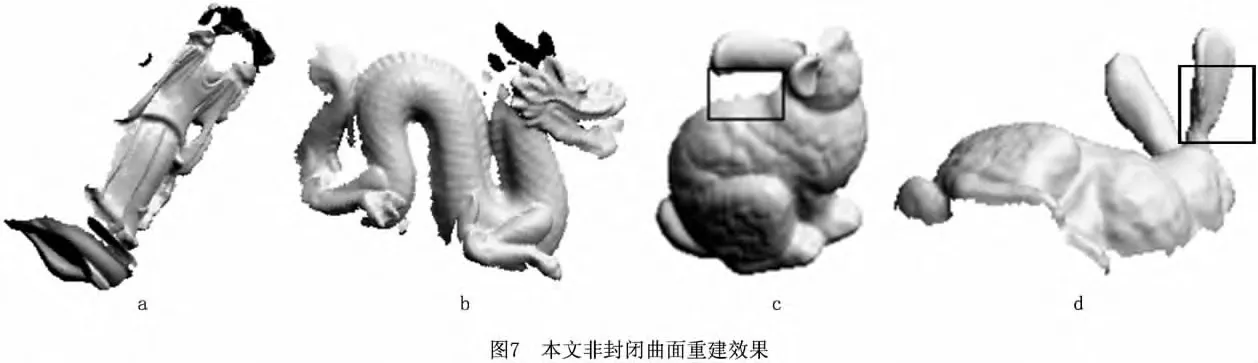
为进一步验证本文算法的有效性，将图5～图7中的点云数据利用基于α－shape的算法进行重建［11］，结果如图8所示。基于α－shape的算法是一种显示方法，当点云质量不好或较稀疏时，基于αshape的结果并不理想，如图8c黑色方框中Bunny模型的耳朵部分重建曲面出现了明显的残缺。而本文所提算法是建立在隐式曲面重建的基础上，因此对点云质量较差和密度稀疏的情况均能获得理想的结果。对比图7c黑色方框中Bunny模型耳朵部分的重建效果可以看出，本文方法能取得更好的重建结果。

5 结束语

本文提出一种自动阈值分割的非封闭曲面三维重建方法，能快速、准确地对泊松算法生成的封闭曲面进行分割，自动去除非封闭曲面重建时生成的多余伪曲面。大量实验证明，使用本算法可得到精确的分割效果，算法的鲁棒性强、算法复杂度低，所需的时间复杂度为O（N），而且算法简单易实现，为泊松曲面重建算法在逆向工程领域中的非封闭点云数据进行直接重建奠定了良好的基础。本文所提方法是在泊松算法重建得到伪封闭模型曲面的基础上，采用阈值分割的方法除去伪曲面而得到与点云一致的非封闭模型。如何能对非封闭点云数据直接进行高质量的曲面重建，进一步提高算法的通用性，是今后研究的重点。

［1］LU Zhen，KE Yinglin，SUN Qing，et al．Extraction of blend surface feature in reverse engineering［J］．Computer Integrated Manufacturing Systems，2003，9（2）：154－157（in Chinese）．［吕 震，柯映林，孙 庆，等．反求工程中过渡曲面特征提取算法研究［J］．计算机集成制造系统，2003，9（2）：154－157．］

［2］CHENG Siyuan，YU Guoxin，ZHANG Xiangwei．Surface model reconstruction methodologies in reverse engineering system［J］．Computer Integrated Manufacturing Systems，2008，14（10）：1934－1939（in Chinese）．［成思源，余国鑫，张湘伟．逆向系统曲面模型重建方法研究［J］．计算机集成制造系统，2008，14（10）：1934－1939．］

［3］SHI Baoquan，LIANG Jin，LIU Qing，et al．Precision inspection of point cloud ＆CAD model based on constraint search sphere［J］．Computer Integrated Manufacturing Systems，2010，16（5）：929－934（in Chinese）．［史宝全，梁 晋，刘 青，等．基于约束搜索球的点云数据与CAD模型精确比对检测［J］．计算机集成制造系统，2010，16（5）：929－934．］

［4］OHTAKE Y，BELYAEV A，SEIDEL H P．Multi－scale approach to 3Dscattered data interpolation with compactly supported basis functions［C］／／Proceedings of Shape Modeling International．Washington，D．C．，USA：IEEE，2003：153－161．

［5］CARR J C，BEATSON R K，CHERRIE J B，et al．Reconstruction and representation of 3Dobjects with radial basis functions［C］／／Proceedings of the 28Annual Conference on Computer Graphics and Interactive Techniques．New York，N．Y．，USA：ACM，2001：67－76．

［6］ZHANG Taohong，HAN Yanling，TU Mengfu，et al．Application of radial basis function net works in reconstruction of virtual machining object［J］．Computer Integrated Manufacturing Systems，2007，13（5）：945－949（in Chinese）．［张桃红，韩彦岭，涂孟夫，等．径向基函数网络在虚拟加工对象重构中的应用［J］．计算机集成制造系统，2007，13（5）：945－949．］

［7］OHTAKE Y ，BELYAEV A，ALEX M，et al．Multi－level partition of unity implicits［C］／／Proceedings of ACM SIGGRAPH．New York，N．Y．，USA：ACM，2003：463－470．

［8］KAZHDAN M，BOLITHO M，HOPPE H．Poisson surface reconstruction［C］／／Proceedings of the 4th Eurographics Symposium on Geometry Processing．Aire－la－Ville，Switzerland：Eurographics Association，2006：61－70．

［9］FU Zhongliang．Some new methods for image threshold selection［J］．Computer Applications，2000，10（10）：13－15（in Chinese）．［付忠良．一些新的图像阈值选取方法［J］．计算机应用，2000，10（10）：13－15．］

［10］The stanford 3Dscanning repository［EB／OL］．（2011－09－06）［2012－01－20］．http：／／graphics．stanford．edu／data／3Dscanrep／．

［11］EDELSBRUNNER H，MUCKE E P．Three－dimensional alpha shapes［J］．ACM Transactions on Graphics，1994，13（1）：43－72．