多级制造过程关键质量特性识别方法

王 宁，徐济超，杨剑锋

（1．西北工业大学 管理学院，陕西 西安 710129；2．郑州大学 商学院，河南 郑州 410052）

0 引言

多级制造过程在现代生产中已十分普遍，指一个系统为制造出最终产品，需经过多个生产步骤、工序或阶段，制造过程中的每一道工序都直接或间接地影响着整个过程的质量保证能力。多级制造过程中存在大量的质量特性，它们之间又存在相关性。由于成本和技术等原因，质量控制人员无法监控全部质量特性。因此，在多级过程质量分析和改进中，首先需要对关键质量特性进行识别。

有关制造过程关键质量特性识别的研究，最早是Boeing公司在实际质量管理过程中基于质量损失的程度来界定关键质量特性［1］。国内近年来较有代表性的研究有：何益海等（2007）［2］提出了基于质量屋的关键质量特性提取方法；张根保等（2010）［3－4］提出了基于人工神经网络（Artificial Neural Networks，ANNs）技术的复杂机电产品关键质量特性的提取模型和制造过程关键质量特性优化模型。国外对多级制造过程关键质量特性识别的研究起步较早，其研究主要集中于模式识别方法和统计建模方法［5］，如 Ding等（2005）［6］应用模式识别方法对汽车主体的多级生产过程中的质量波动进行识别和监控；Tsung等（2008）［7］研究了状态空间波动传递模型应用于多级过程的关键质量特性识别；Loose等（2008）［8］提出了基于多变量测量值的协方差矩阵的特征向量来识别多级过程关键质量特性等。但从当前研究看，国内对制造过程关键质量特性的识别研究多讨论单级过程，较少涉及多级过程。而国外虽有初步研究，但很多学者只考虑单变量情况，忽视了多质量特性之间的相关性问题［9］。最关键的是，目前学者多以串联结构的多级制造过程为研究对象，未研究并联结构下多级过程关键质量特性的识别问题，而具有串并联混合结构的多级制造过程为实践中最常见的形式。

因此，本文在多级制造过程关键质量特性识别中，首先将状态空间模型引入多级过程，详细讨论串并联结构下多级制造过程的建模问题，构建各子过程质量特性与最终过程输出质量特性之间的质量关系模型，即关键质量特性识别模型；其次，借助偏最小二乘回归（Partial Least Squares Regression，PLSR）方法消除子过程质量特性之间，以及子过程质量特性与最终产品质量特性之间的多重相关性，建立各级子过程质量特性与最终产品质量之间的回归模型；最后，通过偏最小二乘（Partial Least Squares，PLS）方法的辅助技术（变量投影重要性指标）识别出对最终产品质量具有决定性影响的瓶颈过程及关键质量特性。

1 多级制造过程质量关系模型

建立多级制造过程质量关系模型是识别关键质量特性的基础。多级制造过程通常包括串、并联两种结构，本文分别建立串联结构和并联结构下的多级制造过程质量关系模型，然后综合得到混联结构的多级制造过程质量关系模型。

1．1 串联结构的多级制造过程质量关系模型

为有效解决多级制造过程中各级质量特性对最终产品质量影响的积累和传递问题，在串联结构的多级过程建模分析中，状态空间模型是应用最广泛的方法之一［10］。状态空间模型较早由Jin和Shi（1999）提出，其核心在于各级过程的质量特性之间通过线性关系进行传递，将三维空间模型转化为二维向量集，并叠加有系统性干扰［11］，如图1所示。

图中k阶段的产品质量特性xk可由k－1阶段质量特性状态向量xk－1和本阶段的质量影响uk共同表示，xk－1既是k－1阶段质量特性状态的输出，也是k阶段质量特性的输入，其中uk彼此独立。随机向量wk表示均值为0的非系统变量即随机误差向量，它与uk（k＝1，2，…，n）相互独立。

依据状态空间思想，相邻两阶段关键质量特性的关系可以表示为

式中：xij（i＝1，2，…，m，j＝1，2，…，k）表示第j阶段中的第i个质量特性；αi，j－1xi，j－1表示从j－1阶段传递过来的第i个产品质量特性对j阶段产品质量的影响；βijuij表示由于j阶段的过程失效导致的本阶段产品质量特性i对产品质量的影响；wj表示j阶段的系统误差。

由于各级子过程的输出通常有多个质量特性，式（1）由向量表示可得串联结构的多级制造过程质量关系模型

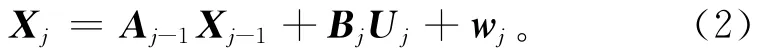
式中：Xj＝ （x1j，x2j，…，xkj）T表示j阶段质量特性向量，Uj＝ （u1j，u2j，…，umj）T表示导致j阶段过程失效的本阶段产品质量特性的向量表示j－1阶段传递的产品质量特性对j阶段产品质量的影响系数矩阵表示j阶段过程失效导致的本阶段产品质量特性对j阶段产品质量的影响系数矩阵。

1．2 并联结构的多级制造过程质量关系模型

在实际生产中，为满足生产率提高和生产线平衡的需要，某一阶段内往往设置多个工序或工位，构成并联结构。图2所示为引用Huang等（2004）描述的一个典型并联结构多级制造过程案例［12］。

图中第一阶段三个工位制成的零部件将会作为输入分别进入第二阶段的两个工位，第二阶段两工位制成的零部件将会作为输入进入第三阶段三个相同的工位。

由于状态空间模型只研究串联结构，而没有对串并联混合结构的多级过程进行分析，本文借鉴Jin等（2010）对并联结构多级制造过程控制方法研究中的思想对传统状态空间模型加以改进，构建并联结构的多级制造过程关键质量特性识别模型［13］。图3所示为具有并联结构的状态空间模型。

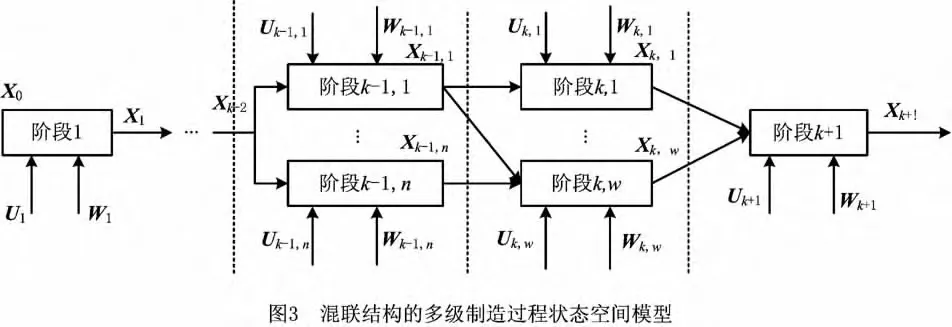
从图中可以看出，并联结构有以下三种情况需要讨论：①平行情况，如k－1阶段第1和n工位质量特性Xk－1，1与Xk－1，n分别为k 阶段第1和w 工位质量特性Xk，1与Xk，w的输入；②分散情况，如质量特性Xk－1，1分别为质量特性Xk，1和Xk，w的输入；③收敛情况，如质量特性Xk，1和Xk，w同时为质量特性Xk＋1的输入。下面对这三种情况分别进行建模分析。

（1）平行情况

平行情况可以看作具有两个输入的串联过程，这两个输入互不影响，其质量关系模型仍可以用串联结构下的状态空间模型表示，并通过递推迭代分别从每一个并行方向继续向前分析，找出上一过程对本过程质量特性的影响，最终形成整个制造过程的线性质量关系模型。

（2）分散情况

在分散情况下，如图3中k－1阶段的一个输出分别作为k阶段两个工位的输入。因此，可以设k－1，1和k－1，2为两个虚拟变量，以辅助表示k－1阶段第一工位质量特性向量［13］，得

（3）收敛情况

在收敛情况下，如图3中k＋1阶段有来自k阶段的两个输入，同样设k＋1，1和k＋1，2为两个虚拟变量，以辅助表示k＋1阶段质量特性向量［13］，得

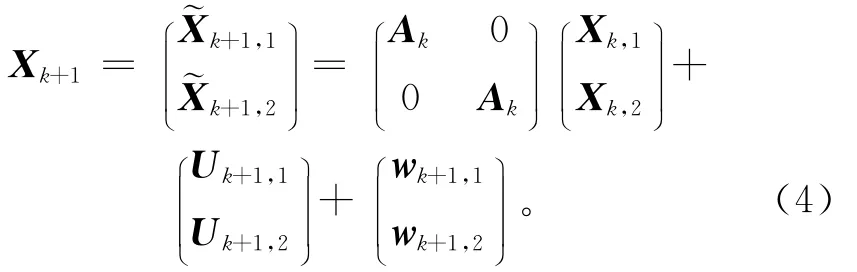
式中：Xk，1和Xk，2表示k阶段两工位质量特性向量，k＋1，1和k＋1，2分别表示基于Xk，1和Xk，2传递过来的质量特性，并且k＋1，1和k＋1，2服从相同的统计分布，它们的和为Xk＋1，即k阶段的质量特性会共同影响k＋1阶段的质量特性。

1．3 混联结构的多级制造过程质量关系模型

由上述质量关系模型可以看出，相邻两阶段质量特性均可以用线性状态空间模型表示。因此，可以通过层级迭代的方法推导出整个混联过程的质量关系模型。仍以图2为例，假设第一阶段的输入均为X0，则可得［13］：

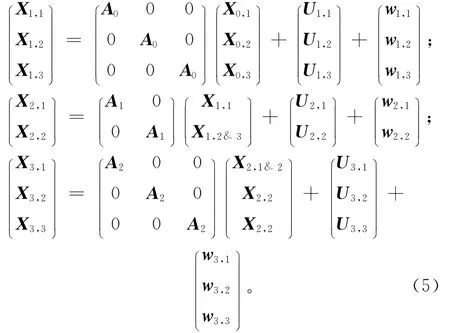
推而广之，设Y为k阶段制造过程的最终产品质量，则根据式（2）～式（4），通过从最终产品质量特性向上一过程依次递推迭代可得

将式（6）归纳整理得

式中：Φ（·，·）为状态转移矩阵，当k＞i时，Φk，i＝Ak－1AK－2…Ai；当k＝i时，Φk，k＝I。当完全展开模型且不考虑系统随机误差wj时，由于X0表示产品进入生产线前的初始状态，如果X0的测量值可以得到，则Φk，0X0可以移到式（4）的左边，Y－Φk，0X0作为新的测量值；若X0不能得到，则可作为一个附加的过程影响输入，不失一般性，则可设X0＝0［14］。式（6）可以简化为

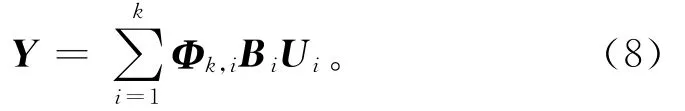
式（8）即为混联结构的多级制造过程质量关系模型。

由式（8）可以看出，不同阶段间复杂的质量特性关系可以通过状态传递来自动处理，最终产品质量可以由各阶段过程质量特性表示。模型仅需要研究在单个阶段中，Xj，Xj－1和Uj这几个变量的相互关系。此时，混联结构多级制造过程质量关系模型可看作是产品质量Y与各个阶段质量特性Uj组成的多元线性方程，如果可以得到每阶段质量特性的影响系数矩阵，就可以识别出哪些质量特性对最终产品质量的影响最大，即要寻找的关键质量特性。

2 基于偏最小二乘回归的建模分析和关键质量特性识别

本文应用多变量PLSR方法解决多级过程质量特性之间存在的大量相关影响，建立起自变量（各级过程质量特性输入向量）与因变量（各级过程质量特性输出向量）之间的回归模型，并通过迭代递推建立最终产品质量特性与各级过程产品质量特性之间的关系模型，最后通过PLSR方法中的辅助技术（变量投影重要性指标）识别出显著因子，确定关键质量特性。具体计算步骤如下：

步骤1 确定多级制造过程最终产品质量要求及各级子过程中对最终产品质量有影响的质量特性，并搜集样本数据。设表示最终产品质量，即因变量。k个自变量1，2，…，k表示k级过程内的质量特性向量，共采集i＝1，…，n组独立的样本数据，（i1，…，ik，）。

步骤2 标准化数据。对数据通过以下公式进行预处理：

式中：Zij为标准化后的数据，Xij为原数据，i为样本均值，si为样本标准差。质量特性样本数据标准化为

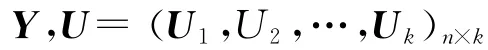
步骤3 对Y进行PLSR分析。从最终产品质量Y开始，根据式（2）～式（4）依次对串并联情况下的各级过程质量特性输入向量与输出向量，使用SIMCA－P软件进行PLSR分析，并根据PLSR的辅助分析技术得到模型的成分数、变量投影重要性指标等相关信息。

步骤4 建立混联结构下的多级制造过程质量关系模型。根据式（5）、式（6）和式（8），从最终产品质量特性向上一级过程依次递推迭代，得到产品最终质量Y与各级质量特性Uj组成的多元线性回归模型，即多级制造过程质量关系模型

式中μi（i＝ 1，…，k）即为式（8）中的影响系数

步骤5 确定关键质量特性。变量投影重要性指标VIPj是在PLSR分析中用于测度自变量在解释因变量时作用的重要性，

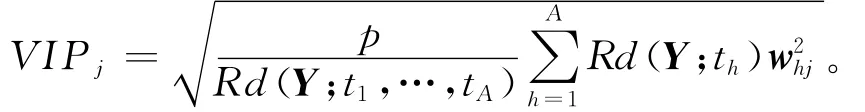
式中：whj表示系统误差wh的第j个分量，用于测量Uj对构造th成分的边际贡献。对于任意h＝1，2，…，A ，有

同时，从VIPj公式的定义上可以看出。当Rd（Y；th）很大时取很大值，则有取较大值。另一方面对于U1，…，Uk，如果在解释Y时的作用都相同，则所有的VIPj均应等于1；否则对于VIPj＞1的Uj，它在解释Y时具有更显著的意义。因此，本文选用VIPj指标识别关键质量特性。

3 实例分析

3．1 实例背景及样本数据

以XZ卷烟厂HJY品牌卷烟的制造过程为例，验证上述方法的正确性和有效性。卷烟制造可分为制丝、嘴棒和卷包三个阶段，其中制丝和嘴棒属于两个并列制造过程，每一阶段又包含有很多工序，是一个典型的混联结构多级制造过程。为便于讨论，本文截取制丝和卷包两个连续阶段来进行说明，其制造流程如图4所示。

依据卷烟产品国家标准的规定，卷烟最终质量分为内在质量和外在质量，其中卷烟吸阻是一个很重要的质量指标，因此选取卷烟吸阻作为最终质量分析对象，即因变量Y；在制丝和卷包过程中，依据历史经验选取制丝过程中的整丝率、碎丝率、纯净度、填充值、水分和卷包过程中的卷烟单只重量、单只重量标偏、卷烟圆周、卷烟硬度，两阶段九个质量特性作为自变量，分别用x11，x12，x13，x14，x15，x21，x22，x23，x24表示。本次共收集13个批号的生产数据作为样本，经标准化后得到样本的标准化数据如表1所示。

表1 样本数据表

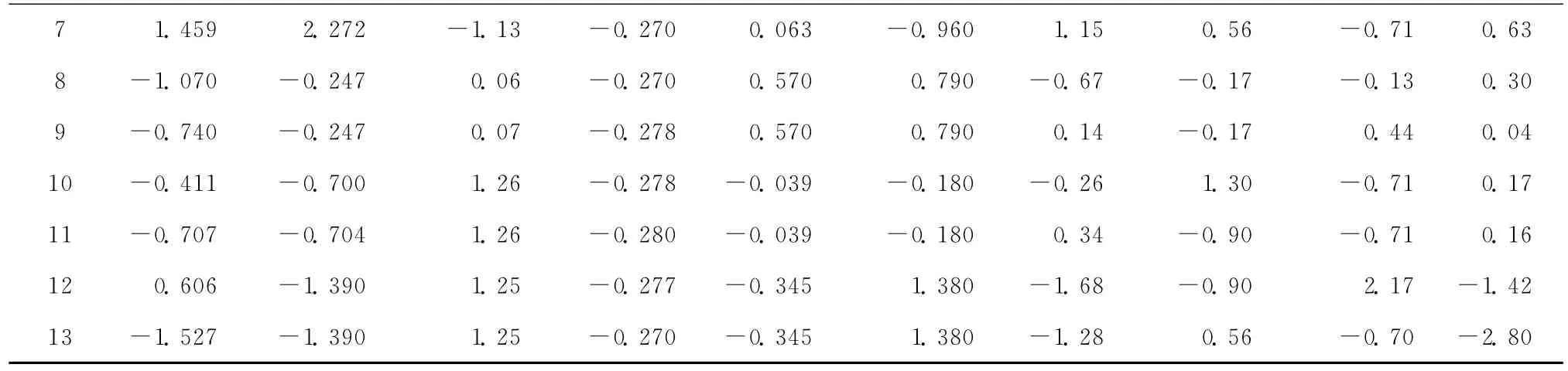
续表1

3．2 模型的构建及分析

制丝和卷包过程为两个连续的串联过程，因此根据式（2）可得

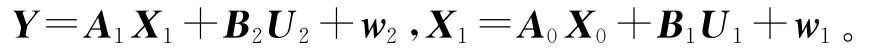
式中：U1＝ （u11，u12，u13，u14，u15）T表示导致制丝阶段过程失效的本阶段产品质量特性向量，U2＝（u21，u22，u23，u24）T表示导 致卷包阶段过程失 效的本 阶 段 产 品 质 量 特 性 向 量，A1＝ ［α1，1α2，1α3，1α4，1α5，1］表示制丝阶段传递过来的产品质量特性对最终产品质量特性的影响系数，B1＝表示制丝阶段的过程失效导致的本阶段产品质量特性对产品质量的影响系数，B2＝ ［β1，2 β2，2 β3，2 β4，2］表示卷包阶段的过程失效导致的本阶段产品质量特性对产品质量的影响系数。

本文设X0为0，且不考虑系统随机误差wj，通过迭代可得两阶段卷烟制造过程质量关系模型

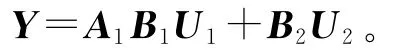
3．3 偏最小二乘回归建模分析

本文采用SIMCA－P软件进行PLSR建模分析，该软件能够支持PLSR的计算和结果解释及辅助分析。具体步骤如下：

步骤1 交叉有效性分析。在PLSR分析中，需要提取部分成分进行建模，目前国内外通常采用交叉有效性分析方法确定提取的PLSR成分数，具体算法见参考文献［17］。图5所示为PLSR的交叉有效性检验结果。

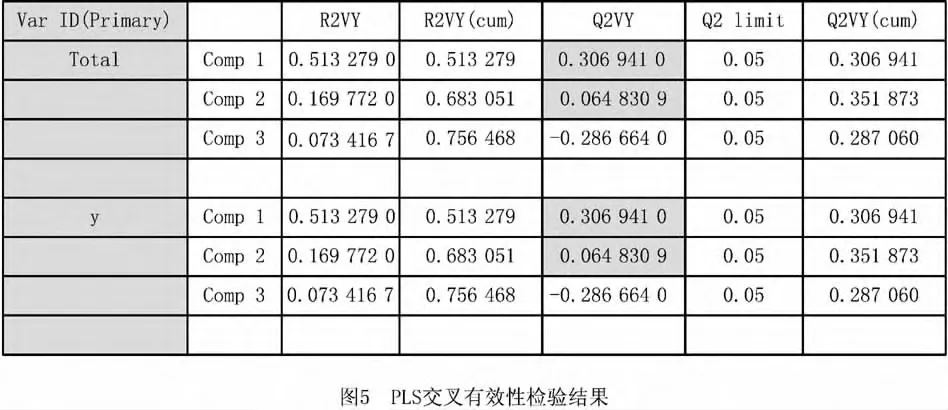
由图5可知，提取的第一个成分对卷烟吸阻Y的交叉有效性是0．306 941，第二个成分的交叉有效性是0．064 830 9，第三个成分的交叉有效性是－0．286 664。因此，系统只提取了两个成分，模型对卷烟吸阻的解释能力为0．756 4，达到了较高的精度。

步骤2 特异点分析。通过特异点分析，可以剔除样本中对回归模型有显著影响的样本点，这里采用T2椭圆图进行特异点分析，图6即为T2分析图。

步骤3 多变量PLSR模型的构建与分析。利用软件提取主成份后，可得到两阶段卷烟制造过程质量关系模型

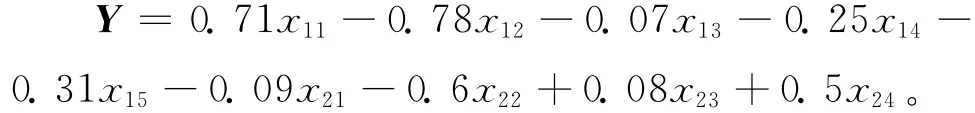
从建立的关键质量特性识别模型中可以看出，x12，x11，x22，x24，x15的回归系数绝对值明显较大，说明这些质量特性对最终产品质量有显著的影响，这些信息将与变量投影重要性指标一起确定关键质量特性。

3．4 识别关键质量特性

经上述分析后，应用变量投影重要性指标VIPj来测度上述模型中各级质量特性Uj在解释最终产品质量的Y时作用的重要性，识别出各级过程中对最终产品质量影响最大的质量特性，确定为关键质量特性。图7所示为本例中的变量投影重要性指标直方图。

从图7可以看出，变量x12（碎丝率）、x11（整丝率）、x22（卷烟单支重量标偏）和x24（卷烟硬度）的变量投影重要性指标超过了1，表明变量x12，x11，x22，x24在解释卷烟吸阻时的作用更大一些，可以判定这四个质量特性为对卷烟吸阻有重要影响的关键质量特性，这与前述关键质量特性识别模型中系数绝对值大小基本一致，同时也与生产过程中的实地调研结果一致。

4 结束语

本文提出的多级制造过程关键质量特性识别方法旨在解决两个问题：①混联结构下，并联多级制造过程质量关系模型的构建问题；②质量特性间的相关性问题。在多级制造过程中，每一级子过程中都有多个不同种类和单位的质量特性，形成混合的变量（质量特性）集合，并且过程的最终输出与不同子过程之间的质量特性都会存在一定的相关性［18］。针对上述问题，本文应用状态空间模型详细分析了混联结构下多阶段制造过程质量关系模型的构建问题，并以PLSR方法为工具消除质量特性间的相关性进行建模分析，应用变量投影重要性指标作为判断依据识别关键质量特性。实例证明，本方法是正确且有效的。本方法存在的不足是：首先质量特性由于受历史经验和现实数据收集的影响，不能更加详细地列出，有些质量特性可能对最终产品无直接影响，但却与关键质量特性具有相关性，因此需要在建模中涵盖更加全面的质量特性；其次多阶段制造过程内质量特性的相互影响有很多非线性的情况，需要继续深入研究。

［1］Boeing．Advanced quality system：key characteristics［S］．Chicago，Ill．，USA：Boeing，1991．

［2］HE Yihai，TANG Xiaoqing．Design for quality based on product key quality characteristics［J］．Acta Aeronautica et Astronautica Sinica，2007，11（6）：1468－1481（in Chinese）．［何益海，唐晓青．基于关键质量特性的产品保质设计［J］．航空学报，2007，11（6）：1468－1481．］

［3］ZHANG Genbao，JI Fuyi，REN Xianlin，et al．Key quality characteristics extraction model of complicated mechanical and electrical products［J］．Journal of Chongqing University，2010，33（2）：8－14（in Chinese）．［张根保，纪富义，任显林，等．复杂机电产品关键质量特性提取模型［J］．重庆大学学报，2010，33（2）：8－14．］

［4］ZHANG Genbao，REN Xianlin，LIU Likun，et al．Multiple key quality characteristics optimization model for manufacturing process［J］．Computer Integr ated Manufacturing Systems，2010，6（16）：1286－1291（in Chinese）．［张根保，任显林，刘立堃，等．面向制造过程的产品多关键质量特性优化模型［J］．计算机集成制造系统，2010，6（16）：1286－1291．］

［5］SHI Jianjun，ZHOU Shiyu．Quality control and improvement for multistage systems：a survey［J］．IIE Transactions，2009，41（9）：744－753．

［6］DING Yu，CEGLAREK D，SHI Jianjun．Fault diagnosis of multistage manufacturing processes by using state space ap－proach［J］．Journal of Manufacturing Science and Engineering，2002，124（2）：313－322．

［7］XIANG Liming，TSUNG F．Statistical monitoring of multistage processes based on engineering models［J］．IIE Transactions，2008，40（10）：957－970．

［8］LOOSE J，ZHOU Shiyu，CEGLAREK D．Variation source identification in manufacturing processes based on relation measurements of key product characteristics［J］．Journal of Manufacturing Science and Engineering，2008，130（3）：1－11．

［9］WU F C．Optimization of correlated multiple quality characteristics using desirability function ［J］．Quality Engineering，2005，17（1）：119－126．

［10］THORNTON A C，DONNELLY S，ERTAN B．More than just robust design：why product development organizations still contend with variation and its impact on quality［J］．Research in Engineering Design，2000，12（3）：127－143．

［11］ZHOU Shiyu，DING Yu，CHEN Yong，et al．Diagnosability study of multi－statge manufacturing processes based on linearmixed model［J］．Technometrics，2003，45（4）：312－325．

［12］ZHOU Shiyu，HUANG Qiang，SHI Jianjun．State space modeling of dimensional variation propagation in multistage machining process using differential motion vectors［J］．IEEE Transactions on Robotics and Automation，2003，19（2）：296－309．

［13］JIN Ming，LI Yanting，TSUNG F．Chart allocation strategy for serial－parallel multistage manufacturing processes［J］．IIE Transactions，2010，42（8）：577－588．

［14］ZANTEK P F，WRIGHT G P，PLANTE R D．Process and product improvement in manufacturing systems with correlated stages［J］．Management Science，2002，48（5）：591－606．

［15］WANG Huiwen．Partial least－squares regression method and applications［M］．Beijing：National Defense Industry Press，1999（in Chinese）．［王惠文．偏最小二乘回归方法及其应用［M］．北京：国防工业出版社，1999．］

［16］WANG Huiwen，WU Zaibin，FENG Jie．Linear and nonlinear partial least－squares regression［M］．Beijing：National Defense Industry Press，2006（in Chinese）．［王惠文，吴载斌，孟洁．偏最小二乘回归的线性与非线性方法［M］．北京：国防工业出版社，2006．］

［17］WOLD S，MARTENS H，WOLD H．The multivariate calibration problem in chemistry solved by the PLS method［C］／／Proceedings of Conference Matrix Pencils，Lectures Notes in Mathematics．Berlin，Germany：Springer－Verlag，1983：286－293．

［18］JIN Nong，ZHOU Shiyu．Data－driven variation source identification of manufacturing processes based on eigenspace comparison ［J］．Naval Research Logistics，2006，53（5）：383－396．