工业CT重建模型与原始CAD模型粗配准的改进
段黎明,王 侃,陈 中
(1.重庆大学ICT研究中心,重庆 400030;2.重庆大学 机械工程学院,重庆 400030)
0 引言
在使用计算机辅助设计(Computer Aided Design,CAD)软件设计产品,建立其原始CAD模型并加工成型后,为判断加工成型后的产品在形状和尺寸方面是否达到设计要求,需要分析加工成型后的产品和原始CAD模型之间的差别。所采用的方法是:首先对产品进行数字化扫描,再根据扫描获取的数据重建其三维数字化模型,然后与其原始三维CAD模型进行比对分析。
目前对产品进行数字化扫描常用的技术有三坐标机测量、超声波测量和工业计算机断层扫描(Computed Tomography,CT)等。其中工业CT扫描技术能以图像形式准确反映工件的内外部情况,且不受工件复杂程度的影响,目前已成为检测复杂产品(特别是含有内腔的产品)的重要手段[1]。由于工业CT对产品进行扫描时有其独立的坐标系,导致重建的三维数字化模型坐标系不同于产品原始三维CAD模型的坐标系,在对这两个模型进行比对分析时,必须首先进行配准。
目前,配准领域多以迭代最近点算法(Iterative Closest Point,ICP)及其改进算法为主[2]。该算法对两模型之间的初始位置要求较高,且很容易陷入局部极值,过早的收敛会导致配准失败[3-4]。而近年提出的利用遗传算法进行配准[5-6]的方法,虽然有较好的全局搜索能力,但耗时较长。无论采取哪种算法,都有必要进行粗配准,以减少两模型之间的平移和角度偏差,在较短时间内尽量使两模型对齐,为精配准提供良好的初始条件。
常用的粗配准方法主要有三点对齐法、最小包围盒法、遗传算法和主成分分析(Principal Component Analysis,PCA)法等。三点对齐法[7]不仅引入了人工操作的误差,不能保证配准结果,还无法实现自动配准;最小包围盒方法[8]仅利用模型的外部轮廓数据,对内部结构不敏感,在配准由工业CT图像重建的模型时,容易忽略工件内部关键结构,导致粗配准成功率较低;遗传算法[9]耗时较长,适用于精配准领域的多次迭代运算而粗配准要求在较短时间内完成的情形。
PCA方法[10]是一种正交化线性变换方法,它将数据变换到一个新的坐标系统中,构成较少的不相关的新变量以代替原始变量,而每个新变量都包含尽量多的原始变量信息,新变量叫作原始变量的主成分或特征向量[11]。对于一个三维刚体,存在特定的表征其质量分布的三个主轴,即三个主方向,而主轴就是惯量矩阵的特征向量。该方法利用两模型点云具有相近的点分布特征进行配准,其经典算法的思路为:计算数据模型的质心及其惯量矩阵的特征向量,并利用质心对齐和主轴对齐,得到平移向量和旋转矩阵,从而完成配准。
文献[12]将PCA方法具体化为力矩主轴法进行粗配准,该方法的优点是运算量小,缺点是对数据缺失比较敏感。工业CT扫描图像重建的三维模型数据完整,适宜采用该方法进行粗配准。文献[13]使用PCA方法对点云数据进行粗配准,提到其反向问题,即由于PCA方法得到的主轴存在两个方向,粗配准的结果可能是其中任意一个,不符合配准预期,易导致配准失败。该文献采用人工旋转模型将其配准到正确方向。文献[14]使用最小包围盒来纠正PCA的反向问题,但同样需要多次翻转计算,时间空间效率较差。本文针对PCA方法的反向问题,以工业CT切片图像三维重建模型的特点为基础,提出基于模型形心和质心矢量关系的PCA修正方法,避免主轴反向的发生。
1 重建模型与CAD模型配准问题的数学描述
利用工业CT对产品进行扫描时,需要根据产品的内外结构情况来确定装夹方式,扫描坐标系不一定与原始CAD模型的坐标系一致,这样根据扫描数据重建的三维数字化模型与其原始的三维CAD模型常常不会处于同一坐标系中。因此,需要对三维重建模型进行空间变换,使其与CAD模型在空间上对齐。
工业CT三维重建模型一般为立体光刻成型(Stereo Lithography,STL)格式的表面模型,它通过大量的三角面片拟合实体表面来表现模型的空间特征,为方便配准计算,将CAD模型离散为表面点云模型。本文假设两模型均已转化为不包含冗余数据的点云模型。
设CAD点云模型为点集矩阵P,工业CT扫描重建点云模型为点集矩阵Q,存在一种刚体变换,使得Q经过该变换得到新点集矩阵Q′后,Q′与P在空间上能够重合,即Q′上任意一点到P的距离最小。配准问题可依此描述为:求得一个空间刚体变换S,且满足distance(S(Q),P)最小[15]。根据计算机图形学理论[16],刚体变换S可由一个旋转矩阵R和一个平移向量T来描述,
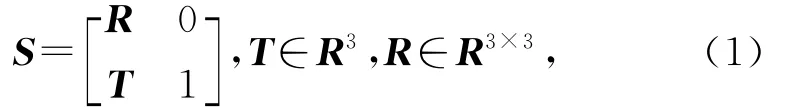
则新点集Q′=Q·R+T。
2 主成分分析配准方法的改进
经典的PCA配准方法具体步骤如下:
(1)求两模型的质心GP和GQ。
(2)根据力学公式分别求出两模型的惯量矩阵IP和IQ。
(3)计算主方向,主方向即为两模型惯量矩阵IP和IQ的特征向量。由于IP和IQ均为实对称矩阵,故其有三个正交的特征向量,即三个正交的主方向。
(4)计算旋转矩阵R。将两组特征向量按特征值的大小分别排列为三阶方阵并单位化,得到EP和EQ,则可通过R·EQ=EP求得旋转矩阵R。
(5)计算两模型间的平移向量T,T即为两模型质心间的矢量。
(6)将旋转矩阵R和平移矩阵T应用到Q上,得到Q′,完成配准。
该经典方法存在一个致命的缺陷,即计算出的两模型惯量矩阵的特征向量没有确定的正负号,导致模型的第二和第三主方向符号不确定,这将对后续旋转矩阵R的求解产生致命影响。在某些情况下主方向会出现反向,求出R并配准后,Q′与P关于某轴线对称,直接导致配准结果与预期严重不符。因此,有必要在PCA配准后判断是否反向,以及出现反向的主方向向量,从而修正配准结果。
2.1 判断是否反向
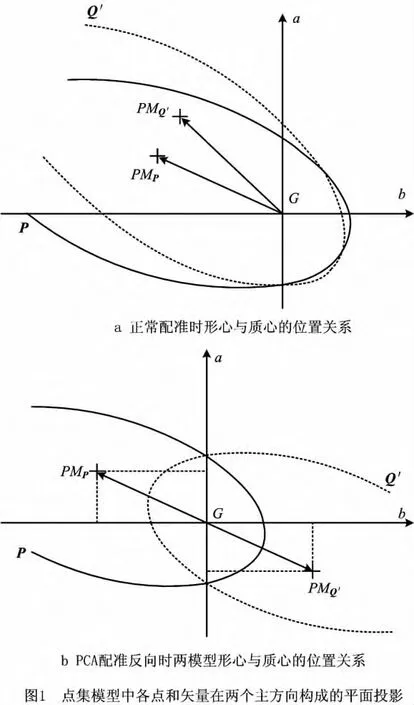
形心和质心作为点集的固有特征,在正确配准时,两点之间的相对位置关系不会随空间刚体的变换而变化。当配准反向时,点云的形心与质心的相对位置关系与正常情况反向,因此该位置关系便可作为一种是否反向的判断标准。图1所示为点集模型中各点和矢量在aGb平面的投影示意图,其中两段弧分别表示点集P和Q′,a和b是P的两个主方向,G是P和Q′配准后共同的质心,PMP和PMQ′分别是P和Q′的形心MP和MQ′在aGb平面的投影点,点集的形心和质心的位置关系在aGb平面内用矢量GPMP和GPMQ′表示。利用PCA配准正常时(如图1a),由于配准误差,GPMP与GPMQ′之间有一定夹角,但两者在a和b方向上不存在方向相反的分量。只有在PCA配准产生反向时(如图1b),两矢量在a轴上的分量会近似地大小相等、方向相反,在b轴上的分量也一样。因此,可以通过对比两点集形心与质心的位置关系,判断出是否有反向情况发生,方法为首先计算由点集形心和质心构成的两个矢量GMP和GMQ′,将它们分别投影在三个主方向a,b,c上,然后判断两矢量在三个方向上的分量,有如下三种情况:
(1)若两矢量在其中一个主方向上的两个投影分量同向,在另两个主方向上的分量分别反向,则判定模型发生了反向,且同向的投影分量所在主方向为旋转轴线。
(2)若两矢量在两个主方向上的投影分量同向,在另一个主方向上的两投影分量反向,则判定配准模型不存在反向问题。
(3)若两矢量在三个主方向上的投影分量分别同向,则判定配准模型不存在反向问题。
2.2 修正反向的点集
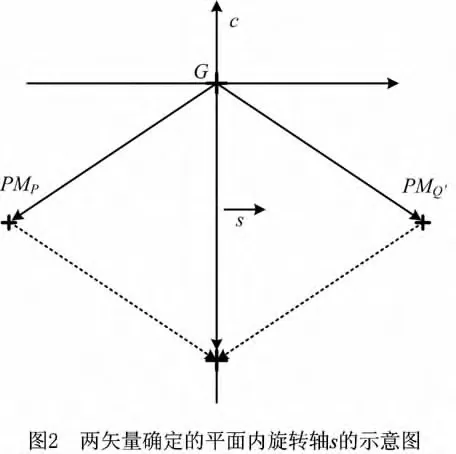
因为PCA配准反向相当于点集Q′绕一个主方向(用c表示)旋转了180°,找出该主方向并逆向旋转180°即可完成修正。如图2所示,在由点集形心和质心构成的两矢量GMP和GMQ′确定的平面内,这两个矢量关于c对称,因此可将两者在平面内的对称轴s作为逆向旋转的轴。

将Q′绕s轴旋转180°,即可完成对反向点集的修正。
2.3 算法步骤
假设已由PCA的前述步骤得到Q′及两点集质心。
步骤1 计算P和Q′的形心MP和MQ′。
步骤2 计算P的形心与质心的距离,若小于一定阈值,则认为两点重合,无法完成后续配准运算,退出;否则,继续步骤3。
步骤3 计算两点集质心与形心的位置关系,用向量表示为u=GMP,v=GMQ′。
步骤4 求得两向量在三个主方向上的分量,ua,ub,uc,va,vb,vc,分别判断ua与va、ub与vb、uc与vc的方向,若有两个主方向上的分量同向,则认为不存在反向情况,结束;若有一个主方向上分量同向,另两方向上分量反向,则认为存在反向,转步骤5。
步骤5 计算u和v之间的对称轴矢量s,将Q′绕s旋转180°,转步骤3。
由此得到的模型点集Q′即为修正后的配准结果。
2.4 方法适用范围
本文通过计算点云模型的形心与质心位置关系来判断是否有反向发生,该方法能够正确配准的前提为点云模型的形心与质心不重合。由于工业CT自身的贯穿性特点,其扫描的产品大多包含内腔,且不规则,质量在空间上分布不均匀,重建出的点云模型形心与质心一般不重合,适合采用本文方法。形心与质心重合的产品使用本方法计算时有可能产生错误,不属于本文方法适用的范围。
3 实验验证
在Windows XP系统中使用VC++6.0开发了实验软件,计算机为主频2.0GHz CPU,1 000 MB内存,图形开发包使用Open Inventor,版本为SIM公司的Coin3D。以下配准实验均在该实验软件下完成。
3.1 实验一
为验证本文方法在PCA方法反向问题上的有效性,选取GE公司公布的Engine Block模型进行配准。对Engine Block切片进行三维重建得到点云模型,包括985 993个点,为方便观察,导入软件后对点云模型进行表面着色渲染,如图3的灰色模型所示;对模型进行一定的空间变换后生成一新点云模型,如图3的黑色模型所示。该发动机模型为腔体类工件,外形轮廓近似长方体,但内部结构复杂,点云的空间分布也不均匀,符合本文方法的适用范围。首先对其使用经典的PCA方法进行配准,配准结果如图4所示,在灰色模型的上侧和燃烧室部分存在明显不匹配的情况,黑色模型由于反向问题而产生上下部分和前后部分的颠倒。使用本文方法配准后的结果如图5所示,图中模型被扭转过来,上部和燃烧室部分都已基本对齐,说明已经不存在方向性的配准错误,解决了PCA方法配准的反向问题。


3.2 实验二

为验证本文方法能满足产品工业CT扫描重建模型与原始CAD模型粗配准的要求,选取某型号化油器进行工业CT扫描,将切片图像进行三维重建得到其点云模型,包括241 964个点,如图6中的黑色模型所示;将该化油器的原始CAD模型离散化为点云模型,包括258 044个点,如图6中的灰色模型所示。化油器模型结构复杂,油路等表面特征无规则,点云的空间分布不均匀,满足本文方法适用范围。使用经典PCA方法配准的结果如图7所示,重建模型背面的法兰盘被变换到了CAD模型正面的进气孔部位。使用本文方法配准,结果如图8所示,两模型的进气孔及上部的凸缘等其他部分已基本对齐,不存在方向性的配准错误,从而得到了正确的粗配准结果。


利用Metro[17]对两点云模型进行点采样,并求出两模型的最大误差为9.584 792mm,平均误差为1.982 866mm,标准误差为2.471 730mm。实验表明,本文方法在完成模型方位正确配准的前提下,能够将配准误差保持在较小范围,为后续精配准提供了较好的初始位置。

3.3 实验三

为了对比本文方法与已有修正PCA反向的方法,通过在本文实验软件平台上编写程序,实现了文献[14]使用的修正方法,并对如图9所示的工件进行粗配准实验。该工件包括51 770个点云。文献[14]通过计算两模型包围盒的重合比例来判断是否反向,若反向则通过翻转模型继续判断,直到该比例超过阈值k。但该方法的比例阈值k的选取直接影响了配准的正确性,图10所示为k分别取60%,80%和95%时该方法的配准结果。可以看出,当阈值k较低,而两模型空间姿态相差较大,且两包围盒重合度较高时,该方法可能会产生误判,没有修正反向问题;当阈值k较高时,又可能出现无法达到阈值的情况,导致配准结果不确定。使用本文方法对两模型进行配准,结果修正了反向问题,如图11所示。表1所示为本文方法与文献[14]方法在配准耗时和方向正确性两方面的对比,本文方法一次配准0.266s得到正确结果,相对文献[14]的方法有较少的耗时和较高的可靠性。



表1 本文方法与文献[14]方法粗配准实验对比
4 结束语
本文根据工业CT扫描对象的特点,通过计算点云模型形心与质心的位置关系,判断并修正PCA方法配准的反向模型。通过对照实验,验证了本文方法能够解决PCA方法配准时的反向问题,在完成模型方位正确配准的前提下,能够将配准误差保持在较小范围,为后续精配准提供较好的初始位置。但本文只研究了不规则工件模型的粗配准问题,规则工件模型的粗配准问题还有待于进一步研究。
[1]DUAN Liming,LIU Yuanbao,WU Zhifang,et al.Method of reconstructing 3-D CAD model based on industrial computed tomography[J].Computer Integrated Manufacturing Systems,2009,15(3):479-486(in Chinese).[段黎明,刘元宝,吴志芳,等.基于工业计算机断层成像技术的三维CAD模型重构方法[J].计算机集成制造系统,2009,15(3):479-486.]
[2]RUSINKIEWIEZ S,LEVOY M.Efficient variants of the ICP algorithm[C]//Proceedings of the 3rd International Conference on 3DDigital Imaging and Modeling.Washington,D.C.,USA:IEEE Computer Society,2001:145-152.
[3]EZRA E,SHARIR M,EFRAT A.On the performance of the ICP algorithm[J].Computational Geometry:Theory and Applications,2008,41(1/2):77-93.
[4]POTTMANN H,HUANG Qixing,YANG Yongliang,et al.Geometry and convergence analysis of algorithms for registration of 3Dshapes[J].International Journal of Computer Vision,2006,67(3):277-296.
[5]LUCIANO S,OLGA B,KIM B.Robust range image registration using genetic algorithms[M].Singapore:World Scientific Publishing Co.,2005.
[6]JING Shikai,CHENG Yunyong,ZHANG Dinghua,et al.Tolerance zone constrained alignment method for turbine blade model[J].Computer Integrated Manufacturing Systems,2010,16(4):883-886(in Chinese).[敬石开,程云勇,张定华,等.一种区域公差约束的叶片模型配准方法[J].计算机集成制造系统,2010,16(4):883-886.]
[7]YAN Sijie,ZHOU Yunfei,PENG Fangyu,et al.Optimization of allowance distribution on the workpieces with large sculptured surfaces in NC machining[J].Journal of Huazhong University of Science and Technology:Nature Science,2002,30(10):35-37(in Chinese).[严思杰,周云飞,彭芳瑜,等.大型复杂曲面零件加工余量均布优化问题研究[J].华中科技大学学报:自然科学版,2002,30(10):35-37.]
[8]LIU Bin,HUA Shungang,OU Zongying,et al.Plate prebending for complete fracture based on automatic registration of fractured bone model[J].Journal of Optoelectronics Laser,2009,20(7):977-982(in Chinese).[刘 斌,华顺刚,欧宗瑛,等.基于断骨模型自动配准的完全性骨折钢板预弯[J].光电子·激光,2009,20(7):977-982.]
[9]YAN Qingguang,LI Mingzhe,LI Dongcheng.Research on registration of 3Ddata in inspection of multi-point forming part[J].China Mechanical Engineering,2003,14(19):1648-1651(in Chinese).[严庆光,李明哲,李东成.多点成形件检测中三维数据配准方法的研究[J].中国机械工程,2003,14(19):1648-1651.]
[10]XU Faqiang,WAN Xiaoxia,ZHU Yuanhong.Color component prediction based on rotated principal component analysis[J].Optics and Precision Engineering,2008,16(3):518-523(in Chinese).[许法强,万晓霞,朱元泓.基于旋转主成分分析的颜色组分预测[J].光学精密工程,2008,16(3):518-523.]
[11]JIANG Ming,ZHANG Guilin,HU Ruolan,et al.Research of an image matching method based on principal component a-nalysis[J].Infrared and Laser Engineering,2000,29(4):17-21(in Chinese).[蒋 明,张桂林,胡若澜,等.基于主成分分析的图像匹配方法研究[J].红外与激光工程,2000,29(4):17-21.]
[12]WU Feng,QIAN Zongcai,HANG Qiashi,et al.Principal axes algorithm based on image contour applied to medical image registration[J].Journal of the Fourth Military Medical University,2001,22(6):567-569(in Chinese).[吴 锋,钱宗才,杭洽时,等.基于轮廓的力矩主轴法在医学图像配准中的应用[J].第四军医大学学报,2001,22(6):567-569.]
[13]SHUI Wuyang,ZHOU Mingquan.An approach for model reconstruction based on multi-view scans registration[C]//Proceedings of IEEE International Conference on Audio,Language and Image Processing.Washington,D.C.,USA:IEEE,2010:601-606.
[14]DAI Jinglan,CHEN Zhiyang,YE Xiuzi,et al.The application of ICP algorithm in point cloud alignment[J].Journal of Image and Graphics,2007,12(3):517-521(in Chinese).[戴静兰,陈志杨,叶修梓,等.ICP算法在点云配准中的应用[J].中国图象图形学报,2007,12(3):517-521.]
[15]MODERSITZKI J.Numerical methods for image registration[M].Oxford,UK:Oxford University Press,2003.
[16]SUN Jiaguang.Computer graphics[M].2nd ed.Beijing:Tsinghua University Press,1995:344-348(in Chinese).[孙家广.计算机图形学[M].2版.北京:清华大学出版社,1995:344-348.]
[17]CIGNONI P,ROCCHINI C,SCOPIGNO R.Metro:measuring error on simplified surfaces[J].Computer Graphics Forum,1998,17(2):167-174.

