基于遗传模拟退火算法的大件公路运输路径选择优化

程 博，杨 育，刘爱军，陈 伟，邢青松

（1．重庆大学 机械传动国家重点实验室，重庆 400030；2．西南交通大学 机械工程学院，四川 成都 610031）

0 引言

在我国国民经济不断稳定发展的新形势下，国家重点建设工程项目的数量和规模都在不断增长，通过公路运输特大、特重型工业设备（如电机转子、变压器和反应器等）已日趋频繁。大件产品由于价格高昂，运输技术要求复杂，对运输安全有极高的要求，决定了大件产品要以最安全最经济的方式送达到客户手中，这对决策者提出了选择最优路径的难题。

杨春兰等［1］研究了大件产品公路运输的安全影响因素，通过数学建模，开发出大件运输计算机决策系统，但没有考虑大件公路运输路径选择问题；徐永能等［2］分析了超载运输与路面可靠度的关系，并建立了基于路面可靠度的超载运输管理模型，但是没有针对具体的路面可靠度进行分析；胡明伟等［3］以最大化服务客户数、最小化客户等待时间和最小化总旅行时间为目标，采用改进局部搜索启发式算法对动态车辆路径规划问题进行求解，但没有涉及大件运输的特殊性；温惠英等分别对遗传算法［4］和粒子群算法［5］进行了改进，并采用改进后的算法对物流配送车辆导航路径优化问题进行研究，有效地解决了点到点的配送优化问题，提高了求解效率，但研究没有考虑运输的特殊性问题；孟凡江［6］采用线性规划方法对铁路运输多路径优化问题进行了研究；高辉等［7］采用改进量子进化算法对路径进行了优化；CESCHIA等［8］采用禁忌搜索算法对包含时间窗和运载成本的混杂路径优化问题进行了研究。后续学者分别采用局部遗传算法［9］、虚拟多项式算法［10］、分支定界法［11］、新的启发式算法［12］、并行算法［13］等对确定和非确定环境下的运输路径问题进行了优化。

综上所述，目前研究大件运输路径优化的文献较少，仅有的基本上也是以最短路径作为最优路径，没有考虑大件运输的特殊性。所采用的优化方法多是对单一算法初始化或者算法结构的改进，缺少基于融合思想的算法改善研究。因此，本文在考虑影响大件公路运输路径选择相关因素的基础上，建立了以最小化成本为目标的规划模型，并采用改进模拟退火算法对大件公路运输路径选择问题进行求解，以确定最佳运输路径方案，为大件公路运输决策者提供参考和支持。

1 大件公路运输路径选择的相关因素

大件产品的公路运输过程非常复杂、技术难度大、耗时长、运输成本十分昂贵，并且对运输的安全性要求极高。根据工程实际，影响大件公路运输路径选择的因素主要包括车辆安全通过性和运输成本两个方面。

（1）车辆安全通过性因素

在大件产品的运输过程中，最重要的就是要保证运输车辆能够安全通过所选路段。一旦在大件运输过程中发生安全事故，事故所造成的损失将是巨大且不可挽回的。影响车辆安全通过性的因素可分为内在因素和外在因素，内在因素主要指车组运行稳定性，外在因素主要指道路通过性和桥梁通过性。

车组运行稳定性又分为横向稳定性和纵向稳定性。货物重心太高，将导致车组允许通过的最大横坡坡度和纵坡坡度减小，一旦所选择的路段含有较多的横坡或纵坡且坡度较大，则很难保证车组的运行稳定性，从而降低运输车辆的安全通过性。

道路通过性主要考虑沿线道路及结构物的路面净空宽度、道路弯道处的转弯半径。由于大件产品一般是超高、超宽、超长的货物，对所选路段的路面净空、宽度和弯道半径有严格要求。若所选路段的路面净空不足，弯道较多，且弯道内外半径不满足车辆转弯所需要的最小道路内外半径，则运输车辆不能顺利转弯，表明车辆在该路段的安全通过性较差。

桥梁通过性主要判别大件运输车辆通过桥梁的可能性，工程中可以采用下式判别车辆的通行能力：其中：S大件表示大件运输车辆产生的截面内力，S标准表示标准载荷产生的截面内力。当θ≤0时，表示运输车辆可以安全通过桥梁；当0＜θ≤5%时，表示运输车辆容许通过桥梁，当θ＞5%时，表示运输车辆不能安全通过桥梁。若所选路段的桥梁数量较多，桥梁承载能力较差，则车辆在该路段的安全通过性较差。

（2）运输成本因素

在进行路径选择时，也要充分考虑运输成本对路径选择的影响。大件运输所要考虑的运输成本不仅包含正常的运输费用，还包括为了增加路段安全通过性而采取的清障、加固、改造等所消耗的费用，这部分费用也可以称为基于车辆安全通过所发生的成本。

影响大件运输成本的因素主要有路段的长度及路段的复杂程度两个方面。所选路段长度越长，运输费用就越高。路段的复杂程度是衡量大件运输车辆通过某路段的难易程度，具有相对性，不同的运输任务，同路段的复杂程度可能不同。大件运输车辆通过路段的坡道越多、弯道的内外半径越小、需要清除的路障越多、桥梁加固越复杂，表明该路段的复杂程度越高。运输车辆在复杂程度高的路段上行驶时，为了确保车辆安全通过，需要清除障碍（交通标志、管廊、树木、建筑物等）、拓宽道路、加固桥梁等，这些保障措施使得运输成本进一步增加。因此，路段的复杂程度越高，所需要的运输成本越高。

2 问题描述及模型建立

2．1 问题描述

大件公路运输路径选择问题为车辆路径问题（Vehicle Routing Problem，VRP），属于典型的复杂组合优化问题。大件公路运输路径选择指根据大件运输的特殊性，将大件产品按客户要求在规定时间T0内从出发地O运往目的地D，主要以车辆及货物的安全通过和降低运输成本两个目标为前提，建立寻找大件公路运输最优路径的模型，为大件运输方提供决策方案。因为在大件运输过程中，发生安全事故会造成巨大且不可挽回的损失，所以车辆及货物的安全通过必须作为优先优化的目标。

2．2 大件运输配送调度数学模型

在建立路径优化模型之前，首先要建立运输网络模型。根据运输任务建立从出发地O到目的地D具有k个节点的运输网络图G＝（V，E）。其中：V表示节点集，E表示网络的边集。图G中的节点Vi与节点Vj之间路段Eij的长度为dij。在选择路径之前，邀请10～15位在大件运输方面有丰富经验的技术人员和专家评估各路段的安全通过性（指道路在清障拓宽加固后的安全通过性）和路段复杂程度对成本及车速的影响大小，并分别建立路段安全通过性集合S、路段复杂程度对成本影响系数集合A＝｛Aij｜0＜Aij≤1｝和路段复杂程度对车速影响系数集合B＝｛Bij｜0＜Bij≤1｝。一般情况下，路段复杂程度越高，对成本、车速的影响越大，成本影响系数和车速影响系数的取值越低。

大件物流配送调度问题描述为：有M个车场，各自拥有Km（m＝1，2，…，M）辆车，负责对N个用户进行大件货物的配送工作，以最小化运输成本、最大化运输安全性为目标，寻求满足所有客户需求的调度方案。

为了方便建模和求解，需要对现实问题进行抽象和简化［14］：

（1）配送中心向多个客户提供送货服务，每个客户的配送需求仅能由一辆大件运输车完成，不允许分批分车配送。

（2）客户需要的货物可以混合配装，但当每个车辆载重的客户货物的总重量超过该配送车辆的最大载重量时就要给予一定惩罚。

（3）配送时每台车辆都从配送中心出发，最终返回原配送中心。

（4）配送中心与客户之间以及客户相互之间的距离已知。

（5）对于客户要求在指定时间窗内完成的配送任务，配送作业提前或者推迟完成都要给予一定惩罚。

（6）路段复杂程度对成本影响系数集合A和路段复杂程度对车速影响系数集合B已知。

（7）配送车辆在配送中心、客户间的行驶时间根据距离和车辆速度可求。

设用户编号为1，2，…，N，车场编号为N＋1，N＋2，…，N＋M，大件公路运输路径优化数学模型表示如下：

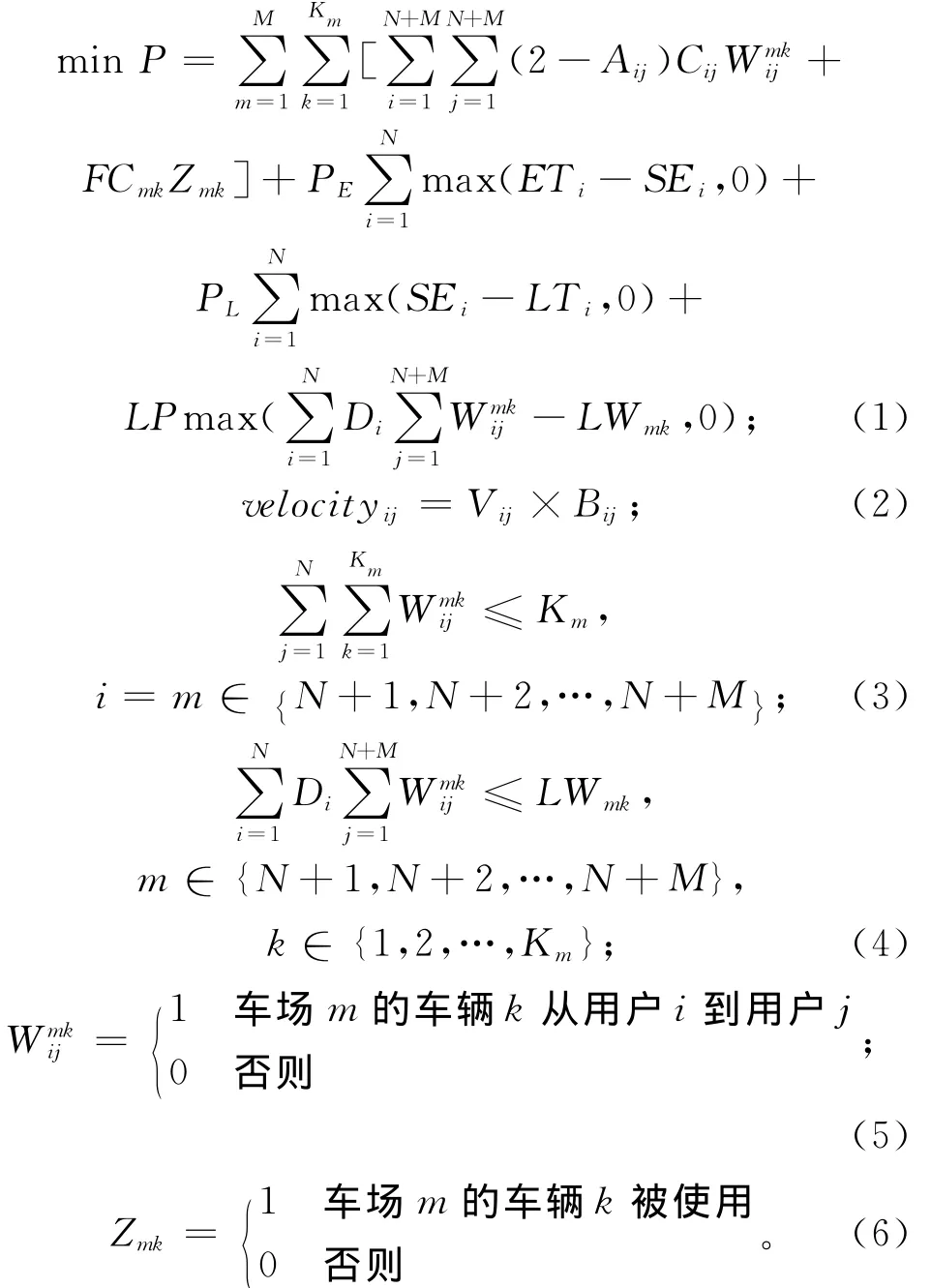
其中：FCmk表示使用车场m的车辆k的固定成本；LWmk表示车场m 的车辆k的载重量限制；［ETi，LTi］表示第i个用户的服务时间窗，ETi为用户i的服务最早开始时间，LTi为用户i的服务最迟开始时间，如果车辆到达i的时间早于ETi，则车辆需在i处等待，如果车辆到达时间晚于LTi，则要延迟进行；SEi表示第i个用户的实际服务开始时间；PE为提前惩罚系数，PL为延迟惩罚系数；LP为超重惩罚系数；Cij表示从用户i到用户j的运输成本；Vij表示从用户i到用户j的运输速度；velocityij表示考虑路段复杂程度以后的校正车速。

配送调度问题除了要满足以上目标函数和约束以外，还要满足以下性能：

（1）空驶里程Z

配送车辆把货物配送完成返回车场的路途长度就是空驶里程，空驶里程对配送中心来说是不产生任何价值的浪费环节，因此在配送优化满足目标的方案中，空驶里程越短，方案越优。

（2）线路平均长度L－

线路的平均长度反映了车辆运行负荷的基本情况，在满足目标的情况下，线路平均长度越短，方案越优。

（3）线路均衡度ψ

线路均衡度是最短线路长占最长线路长的百分比，反映最长与最短线路的差异性。

3 改进遗传模拟退火算法

目前，物流配送领域的相关研究多采用性能稳定的遗传或模拟退火算法为基础组成的混合算法，这两类算法分别具有优良的搜索优点：① 遗传算法具有自组织、自适应、自学习能力及搜索并行性的优点；②模拟退火算法具有优良的局部搜索能力，即在搜索最优解的过程中，除了可以接受优化解外，还可以有限度地接受部分恶化解，并且可以使接受恶化解的概率逐渐趋向于0，从而使算法有可能从局部极值区域中跳出，找到全局最优解，并保证算法的收敛性。这样，通过两种算法混合构造新的遗传模拟退火算法可以达到扬长避短的作用。

综上所述，本文将在已有遗传模拟退火算法研究的基础上，通过折中优化质量和优化效率的策略确定初始温度，改善搜索冗长的现象，增强进化速度；采用自适应交叉和变异处理方法，提高遗传算法局部搜索性能，增强进化能力；通过对交叉和变异后的个体实施接受策略，增强遗传算法的全局收敛性，加快进化后期的收敛速度，采用在每次迭代结束前进行降温处理的方法，保证遗传算法和模拟退火算法具有相同的收敛方向和速度。算法结构如图1所示。

具体操作步骤如下：

步骤1 给定种群规模popsize，k＝0；从产生的初始解中选择最大、最小目标函数值f0，max和f0，min，计算初始温度，产生满足载重和体积约束的初始群体pop（popsize）；计算目标值f（i），找出使目标函数值最小的染色体i和该函数值f，记i＊＝i，f＊＝f；其中，i为当代群体中的一个染色体。

步骤2 若满足约束，则输出最优染色体i＊和最优解f＊，运算停止；否则在群体pop（popsize）的每一个染色体i的邻域中随机选取一个状态j∈N（i），按照模拟退火中的接受概率

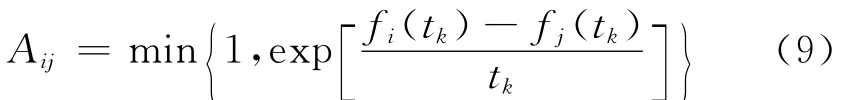
接受或拒绝j，其中fi（tk）和fj（tk）分别表示状态i和j在温度为tk时的目标值。这一阶段共需popsize次迭代来选出新群体pop1（popsize）。

步骤4 分别以自适应pC和pM对pop2（popsize）进行交叉和变异操作。

步骤5 计算pop2（popsize）中个体的目标函数值，找出函数值最小的染色体χ及该函数值λ，如果λ＜f＊，则令i＊＝χ，f＊＝λ，μ为退火率，tk＋1＝μtk，k＝k＋1，返回步骤2。

4 算法设计

4．1 算法编码

由于遗传模拟退火算法不能直接处理解空间的数据，必须通过编码将其表示成基因型串结构数据［15］。本文以客户为中心，提出三层染色体编码新方法，能够表示不同数量的车场、车辆和线路安排信息值，使算法可以对车场、车辆及路线进行自动寻优。

染色体采用自然数编码，即序数编码，染色体表示为基因序列 （G1，G2，…，GN），其中Gi由车场编号 M－number、车 辆 编 号 Km－number 和 排 序 值Val－number三部分组成。该染色体表示了车场、车辆和线路安排信息，如编号为i的客户需要由车场M－number的编号为Km－number的车辆运载，其在路径中的位置由排序值Val－number的大小来决定。这种方法没有明确地表示出每辆车的确切路径，但是每辆车的确切路径隐含在Val－number排序中。

4．2 选择算子

轮盘赌用来从染色体群体中选择成员，被选中的几率与其适应性分数成比例。该方法的基本思想是：生成一个随机数γ∈［0，1］，并计算个体的相对适应度值pi＝fi／∑fi，如果p0＋p1＋…＋pi－1＜γ≤p0＋p1＋…＋pi，则第i个个体被选择到下一代。可见，个体的适应度值越大，被选择到下一代的机会也越多。

4．3 交叉与变异算子

遗传算法的参数中，交叉概率PC和变异概率PM的选择直接影响算法的收敛性，是影响遗传算法行为和性能的关键。PC越大，产生新个体的速度就越快，会很快破坏具有高适应度的个体结构；若PC过小，则会使搜索过程变得缓慢，甚至停滞不前。对于变异率PM，如果PM过小，则不能维持种群的多样性，造成算法过早收敛；如果PM取值过大，则会破坏接近最优解的遗传模式。为了避免选用这种固定交叉和变异概率，本文采用一种自适应调整交叉和变异概率的方法，具体方法如下：

（1）自适应交叉算子

交叉操作是遗传算法中增加种群多样性、防止算法早熟和停滞的操作。研究发现，在进化的过程中，当前代种群中个体的适应度值低于平均适应度值时，需要提高交叉概率；当适应度值高于平均适应度值时，则需要降低交叉概率。这样就使交叉概率随着适应度值自动地调整，既克服了不成熟的收敛，又避免破坏优秀染色体。为此，本文提出交叉概率动态调整策略，交叉概率的自适应调整公式为

（2）自适应变异算子

变异是按一定的概率改变个体基因链，变异操作也是增加种群多样性的一种进化手段，适度的变异既能保持种群内个体的多样化，又能提高算法的效率，克服遗传操作可能限于局部解的弊端。为了克服PM过大或过小的弊端［16］，本文采用与PC相似的处理方式自适应调整PM，变异概率的自适应调整公式为：

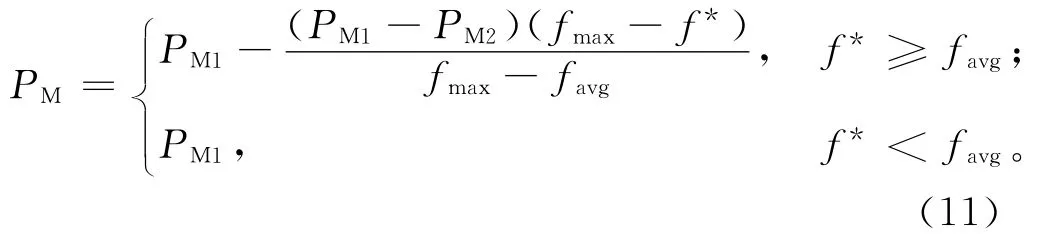
式中：fmax为群体中最大的适应度值，favg为每代群体的平均适应度值，f为交叉的两个个体中较大的适应度值，f＊为要变异的个体的适应度值。

由上述自适应交叉和变异概率可实现种群的多样性，保证算法搜索空间的广泛性，在此基础上对本文的配装配送调度问题实施双点交叉，在个体编码串中随机设置两个交叉点，然后再进行部分基因的交换。设选择进行交叉的父、母体分别为X和Y，经双点交叉得到后代X′和Y′，双点交叉示意图如2所示。

为提高收敛速度，变异过程采用简单快速的移位变异方式，如图3所示。

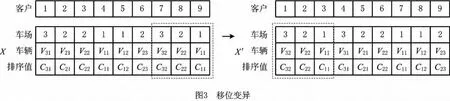
经上述双点交叉和移位变异操作产生的新个体可能违背了载重和体积限制条件，因此必须对产生的新个体进行载重和体积约束验证，如果不能满足约束条件，则重新产生交叉或变异个体，直至达到popsize个个体。

5 实验数据与分析

基于上述改建遗传模拟退火算法的研究，结合大件公路运输路径优化模型，以最小化总成本为目标进行仿真。以某公司大件公路运输为例，该公司具有两个配送中心，需要将大件设备运输到10个客户手中，选择出总成本最小的运输路线。首先根据路面净空、宽度、弯道半径和桥梁通过性对路径进行初选，选择出如表1所示的运输路径。算法相关参数设置如下：种群规模popsize＝100；超载罚函数LP＝200；时间窗惩罚函数系数PE＝20，PL＝20；交叉率计算参数PC1＝0．9，PC2＝0．6；变异率计算参数PM1＝0．1，PM2＝0．001；模拟退火算法退火率μ＝0．85。各客户货物相关信息、各车场车辆信息及路段复杂程度对成本和车速的影响系数集合A和B如表2～表4所示。

表1 配送中心及客户之间的距离

表2 各客户货物相关信息

续表2

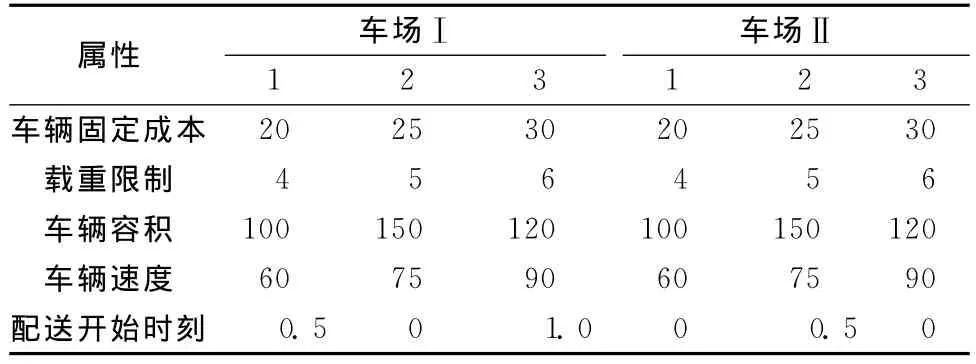
表3 各车场车辆信息

表4中括号内的两个数据，前者表示成本系数，后者表示速度系数。运用本文的改进遗传模拟退火算法对实验数据进行仿真优化，种群迭代200次得到的目标函数最优的染色体为：

函数极值为Result＝1．430 4×103。

Solution中，三个数据为一组，依次表示10个客 户，如 客 户 1 的 数 据 集 （1．000 0，3．000 0，0．143 7）中的数据分别表示：客户1的配送活动由Ⅰ号配送中心执行；该配送中心选择该中心的第3辆车执行配送活动；客户1在该车配送中的优先级数为0．143 7。如最优染色体所示，得到的调度方案为：Ⅰ号配送中心第2辆车的配送路线为Ⅰ－10－8－Ⅰ；第3辆车的配送路线为Ⅰ－3－1－Ⅰ；Ⅱ号配送中心第1辆车的配送路线为Ⅱ－7－2－Ⅱ；第2辆车的配送路线为Ⅱ－6－9－Ⅱ；第3辆车的配送路线为Ⅱ－5－4－Ⅱ。配送路线如图4所示，有I和Ⅱ两个配送中心完成物流的配装配送任务，括号内的数据表示车场和车辆标志，如（Ⅰ，2）表示第Ⅰ个车场的第2辆车来执行客户10和8的配装和配送任务，在这种调度方案下，目标函数的最优解为1 430。为评价本文改进遗传模拟退火算法的性能，将其与文献［17］的基本遗传算法（种群规模为100，交叉概率为0．75，变异概率为0．25）及文献［18］的遗传退火算法进行比较，运行10次得到的目标函数值如表5所示。

从表5中的数据可知，经10次运行，本文的改进遗传模拟退火算法得到的平均结果1 440．3优于遗传算法所得的平均结果1 529．5，同时优于文献［18］的遗传退火算法所得的平均结果1 457．4，且有5次得到了该问题的最优解1 430。可见，利用本文改进遗传模拟退火算法可以方便有效地求得多约束条件下的物流配送路径优化问题的最优解或近似最优解。

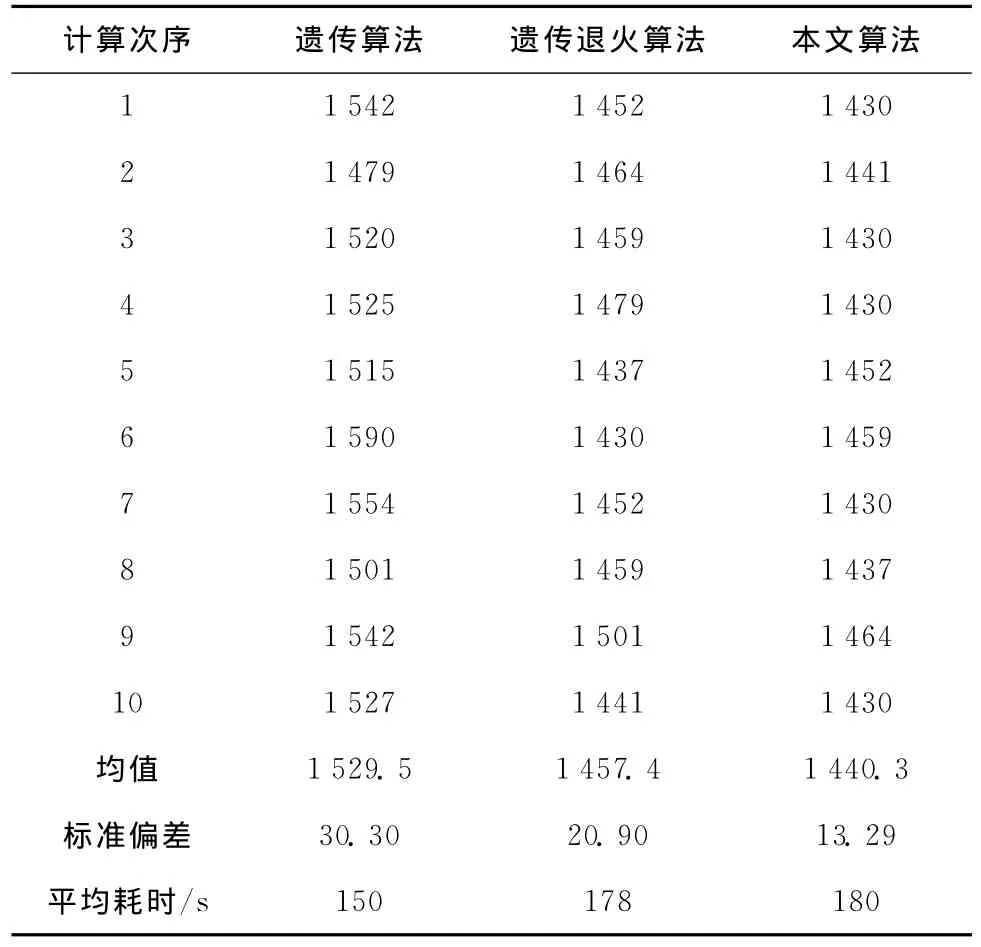
表5 算法性能对比

为充分认识本文改进遗传模拟退火算法对线路均衡性等配送性能的影响，多次运行程序，得到算法性能分析如表6所示。

表6 算法性能分析

由表6可知，随着运算代数的增加，目标函数值趋向最优值，载重和体积利用率逐步得到优化；在最小化目标函数值的条件下，派出车辆数、空驶里程长度和线路平均长度经历变化，最后收敛到较优值；由于目标函数的影响，线路最大偏差度和线路均衡度向理论最优值的反方向变化。由上述分析，调度者可以根据物流配送的实际情况做出费用决策和距离决策的权衡。

6 结束语

本文针对大件公路运输路径优化问题，建立了多目标物流配送数学模型，提出了改进的遗传模拟退火算法，通过大量的仿真试验计算，取得以下成果：

（1）在求解大件公路运输路径优化问题方面，本文结合大件物流运输的特点，克服了目前研究只针对配送路径进行优化的缺陷，建立了带配送时间窗、客户服务时限、车辆超载惩罚、车辆服务时限、车辆载重限制、车辆容积限制、车辆安全通过性等多约束条件下的大件公路运输路径优化模型，给出了求解该类问题的思路。

（2）在该算法的设计和实现方面，采用三层序数编码方法产生满足载重和体积约束条件的初始种群，保证每个染色体的可行性，通过模拟退火操作和遗传算法的选择、交叉、变异等操作，对整个群体进行优化。其中，引入自适应参数策略，动态调整交叉和变异概率，既克服了不成熟的收敛，又避免了优秀染色体被破坏。

（3）在算法性能方面，以大件公路运输问题为例，分别采用遗传算法、遗传退火算法和改进遗传退火算法进行求解，通过对调度结果进行分析发现，改进遗传退火算法具有更好的全局寻优能力和更小的标准偏差，同时验证了本文提出的改进遗传模拟算法在求解多约束条件多目标配送优化问题时的优越性。

本文针对公路大件运输路径优化问题进行了深入研究，在建模过程中，对路径选择方法进行了必要的简化处理。下一步可以围绕路径通过性问题，将路径的路面承载能力、摩擦系数、最大上坡坡度、最大下坡坡度及弯道半径等因素考虑到优化模型中，以期进一步提升该算法的工程指导意义。

［1］YANG Chunlan，HUANG Dongsheng，ZHANG Yu，et al．Modeling and software developing for computer decision making system of road massive products transportation［J］．Journal of Wuhan University of Technology：Transportation Science＆Engineering，2003，27（1）：106－108（in Chinese）．［杨春兰，黄东胜，张 雨，等．公路大件运输计算机决策系统建模与软件开发［J］．武汉理工大学学报：交通科学与工程版，2003，27（1）：106－108．］

［2］ZHONG Shiquan，DU Gang．Open vehicle routing problem based on kernel route tabu search algorithm［J］．Computer Integrated Manufacturing Systems，2007，23（4）：132－142（in Chinese）．［钟石泉，杜 纲．基于核心路径禁忌算法的开放式车辆路径问题研究［J］．计算机集成制造系统，2007，23（4）：132－142．］

［3］HU Mingwei，TANG Hao．Multi－objective optimization model of dynamic vehicle routing problem［J］．Journal of Shenzhen University Science and Engineering，2010，27（2）：230－235（in Chinese）．［胡明伟，唐 浩．动态车辆路径问题的多目标优化模型与 算 法 ［J］．深 圳 大 学 学 报：理 工 版，2010，27（2）：230－235．］

［4］WEN Huiying，XU Jianmin，LIN Zhengchun．Genetic algorithm for route optimization of vehicle navigationin logistics distribution［J］．Journal of South China University of Technology：Natural Science Edition，2009，37（2）：82－91（in Chinese）．［温惠英，徐建闽，林正春．适于物流配送车辆导航路径优化的遗传算法［J］．华南理工大学学报：自然科学版，2009，37（2）：82－91．］

［5］WEN Huiying，LI Junhui，ZHOU Weiming．Improved particle swarm optimization algorithm for vehicle routing planning［J］．Journal of South China University of Technology：Natural Science Edition，2009，37（7）：1－5（in Chinese）．［温惠英，李俊辉，周玮明．适于车辆路径规划的改进型粒子群优化算法［J］．华南理工大学学报：自然科学版，2009，37（7）：1－5．］

［6］LI Yanhui，LIU Xiang．Modelling and its ant colony algorithm for multi－depot open vehicle routing problem with replenishment on the way［J］．Computer Integrated Manufacturing Systems，2008，11（3）：25－34（in Chinese）．［李延晖，刘 向．沿途补货的多车场开放式车辆路径问题及蚁群算法［J］．计算机集成制造系统，2008，11（3）：25－34．］

［7］JIANG Changhua，DAI Shugui，HU Youhua．Hybrid genetic algorithm for capacitated vehicle routing problem ［J］．Computer Integrated Manufacturing Systems，2007，14（10）：237－248（in Chinese）．［姜昌华，戴树贵，胡幼华．求解车辆路径问题的混合遗传算法［J］．计算机集成制造系统，2007，14（10）：237－248．］

［8］CESCHIA S，DI G L，SCHAERF A．Tabu search techniques for the heterogeneous vehicle routing problem with time windows and carrier－dependent costs［J］．Journal of Scheduling，2011，14（6）：601－615．

［9］URSANI Z，ESSAM D，CORNFORTH D．Localized genetic algorithm for vehicle routing problem with time windows［J］．Applied Soft Computing，2011，11（8）：5375－5390．

［10］ZIAUDDIN U，DARY E，DAVID C，et al．Localized genetic algorithm for vehicle routing problem with time windows［J］．Applied Soft Computing，2011，11（8）：5375－5390．

［11］MACEDO R，ALVES C，VALERIO D．Solving the vehicle routing problem with time windows and multiple routes exactly using apseudo－polynomial model［J］．European Journal of Operational Research，2011，214（3）：536－545．

［12］SALANI M，VACCA I．Branch and price for the vehicle routing problem with discrete split deliveries and time windows［J］．European Journal of Operational Research，2011，213（3）：470－477．

［13］LIN C．A vehicle routing problem with pickup and delivery time windows，and coordination of transportable resources［J］．Computers ＆ Operations Research，2011，38（11）：1596－1609．

［14］MENDOZA J．Solving real－world vehicle routing problems in uncertain environments［J］．4OR－A Quarterly Journal of Operations Research，2011，9（3）：321－324．

［15］GULCZYNSKI D，GOLDEN B．WASIL E．The period vehicle routing problem：new heuristics and real－world variants［J］．Transportation Research Part E－Logistics and Transportation Review，2011，47（5）：648－668．

［16］GROER C，GOLDEN B，WASIL E．A parallel algorithm for the vehicle routing problem［J］．Informs Journal on Computing，2011，23（2）：315－330．

［17］WU Jingli，LIU Renhui．Genetic algorithm for batch vehicle routing problem with time windows［J］．Computer Engineering，2006，32（8）：213－218（in Chinese）．［吴璟莉，刘仁辉．分批配送的有时间窗车辆路径问题的遗传算法［J］．计算机工程，2006，32（8）：213－218．］

［18］WANG Pengtao，LIU Yanliang，WU Jing．Solving logistics transportation based on genetic simulated annealing algorithm［J］．Journal of Computational Information Systems，2008，4（2）：559－564．