不确定环境下创新性产品供应链生产能力决策模型

蔡建湖，王欢欢，韩 毅，林华珍，邓丽丽

（1．浙江工业大学 经贸管理学院，浙江 杭州 310023；2．华中科技大学 管理学院，湖北 武汉 430074）

0 引言

在全球经济背景下，社会分工越来越细，企业的成功越来越依赖于合作伙伴的支持与配合，企业之间的长期合作与信任关系是实现供应链世界级运行绩效的关键［1－2］，尤其是在创新性产品供应链中，新产品生产涉及大量的软硬件投入，同时新产品的市场需求并不是很稳定。因此，制造商面临的供应链风险比较大，寻求与购买商之间的合作成为很多制造商需要考虑的重要决策内容。从制造商的角度来看，需要在不确定环境下确定合理的生产能力设置，这些生产能力设置需要企业投入大量资金进行人力、物力等方面的准备，生产能力的大小直接决定着企业的产出能力［3－4］。类似的生产能力设置问题在创新产品、应急产品等领域尤为突出［5］。实际上，合理的生产能力规划一直是制造型企业关注的重点［6］。在供应链管理背景下，有竞争力的生产能力设置依赖于成员企业之间的合作。因此，很多企业开始关注与供应链上关联企业之间的协同创新。实际上，创建供应链上成员之间合作关系的核心是实现双赢，为此必须引入合适的供应链运作机制。以美国宾夕法尼亚大学沃顿商学院教授Cachon为代表的众多学者提出引入供应链契约来协调与优化供应链性能，这些契约包括收益分享契约、数量契约、通道回扣契约和回收契约等［7］。国内很多学者在这方面也做了一些改进工作，分析了供应链中各种基于契约的竞争模型与优化思路［8－10］。

在现实经济活动中，供应链成员之间的交易行为比传统契约描述的更为复杂，企业之间的业务往来也常表现为更加松散的关系型交易模式。例如，日本东芝很多新产品的初始设计到后来常常会发生较大改变，东芝在大规模生产开始前无法与其供应商形成正式的契约。因此，东芝往往在产品设计初期，向其电子元件供应商非正式地承诺电子元件的价格，这可以给供应商提供足够的时间来为生产做准备。东芝自身的信誉以及与供应商多次交易表现出的诚信，使得其供应商相信东芝的承诺，并据此进行生产准备［11］。在浙江省，一些中小企业也面临着类似的问题，当公司打算开发一种新产品时，或者在新产品开发过程中，公司会尽力接触客户并与客户谈判，给予这些客户在价格和供应方面的承诺，而客户也会与公司签订年度框架协议，协议中规定一年大致多少订购量，或者至少将购买多少量。因为新产品细节未定，产品也没有大批量生产，无法签订严格的法律合同，所以签署的这种框架协议一般是约束力不强的约定，但是这种约定具有极为重要的意义，尤其是在一个竞争的市场环境中。Macaulay（1963）［12］很早就发现，在采购活动中，很多企业采用非正式协议来代替正式的、具有法律效力的正式契约。在这种背景下，各种形式的承诺条款开始引入正式契约中，传统的正式契约中的条款部分或全部被承诺性质的条款替代。这种“带有承诺条款的契约”在众多学者的研究中常直接表述为承诺契约（commitment contracts），多数学者都认可“承诺”是关系型契约（relational contracts）中的条款，它是一种约定或者是一种信任，可以不用严格的法律条文确定下来。关系型契约一直作为经济学中的一个概念，用来分析企业之间的经济关系。Baker等（2001）［13］认为，关系型契约作为一种非正式的协议，在企业之间得到了广泛流行，关系型契约的柔性能够解决一些正式契约难以解决的难题。例如，关系型契约可以根据企业合作的实际结果来作为契约履行的依据，增强契约实施的灵活性。实际上，公司内外到处都有关系型契约的影子，有时承诺契约也可以直接用于最终消费者。Su等（2008）［14］的研究发现，通过事先向最终消费者承诺特定的价格或者特定的供应量，零售商能够获取更高的收益，这类似于生活中常见的高价策略和限量供应策略，具有很强的现实性。Hofenk等（2011）［15］从实证研究的角度分析了关系型要素对增强第三方物流公司竞争力的影响，进一步论证了信任和承诺在供应链合作机制中的重要地位。

随着创新性产品在当前经济生活中所占比重的不断增加，企业面临的不确定环境也在不断增强。而承诺契约强调契约执行的松散性，更加灵活多样，适应了创新性产品发展的需求，因此开始在供应链运作中广泛应用。在 Durango－Cohen 等（2006）［16］构建的模型中，承诺条款为客户的最少订购量，以及制造商承诺的最小配送量。契约要求购买商根据其向供应商提供的预测量，必须按比例确定其最少购买量，而制造商要承诺一个最小配送量。这里涉及到的契约条款所描述的“至少”、“最小”等约定，为供应链运行带来了柔性。Anand等（2008）［17］研究了一个两期库存决策模型，并引入一个批发价承诺契约。在其构建的模型中，批发价承诺表现为供应商在第一期期初，同时确定接下来两期的批发价，这种事先约定在一定条件下优化了供应链的性能。蔡建湖等（2011）［18］引入一个不确定环境下的两级供应链模型，分析了提前订购量承诺契约，并引入针对提前承诺量中超出实际需求部分的价格折扣策略，但是没有考虑批发价的取值范围对订购量承诺契约的影响，也没有考虑针对购买商所有承诺量的价格折扣问题，也没有涉及折扣因子变动时供应链成员的最优决策。

以上文献从不同的角度对承诺型契约进行了探索，然而这些研究仍然存在着诸多待改进的研究工作。例如，承诺契约并不是在任意条件下都适合优化供应链的性能，现有研究仍然没有明确承诺契约到底在什么条件下有利于供应链性能的改进。除此之外，有无比较简单易行的改进对策可以进一步优化一个传统承诺型契约，也是值得研究的问题。本文构建了一个不确定环境下的两级供应链竞争模型，以创新性产品供应链为研究对象，供应商需要确定最优的生产能力设置。研究引入订购量承诺契约之后供应链的最优决策情况，并讨论不同批发价取值对订购量承诺契约适用性的影响，论证引入承诺契约来优化供应链性能的Pareto区间的存在条件；进一步讨论价格折扣策略对订购量承诺契约设计的影响，分析不同折扣因子条件下供应链决策情况的变化，寻求供应链性能的进一步改进。本文还考虑折扣因子大于1时的决策情形，发现此时在一定条件下，承诺契约仍然是有效的。

1 模型的建立

考虑一个两级供应链模型，该供应链由一个供应商和一个购买商组成。该供应商是一个制造型企业，现在由它决定生产某种新产品。为此，供应商需要事先购买大量的设备，招聘一定的员工，这些生产资源的数量和质量往往决定了企业最终的生产能力，在确定生产能力时企业还面临着需求的不确定性。这里，供应链面临的不确定需求用D表示，其分布函数为F（x），密度函数为f（x）。假设供应商单位生产能力的设置成本为C1，进一步假设供应商生产出来的产品的单位批发价为Wa。购买商在市场上销售产品时，产品的零售价格为P，未满足客户需求给购买商带来的单位惩罚费用为Hr。这里有P＞Wa＞C1。定义h＋＝max（0，h），E｛·｝表示求数学期望值。首先考虑供应链集成时的决策问题，它所面临的目标函数为

因此集成供应链最优的生产能力Ka满足

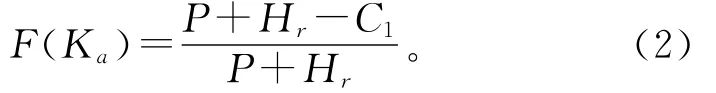
供应商需要在不确定环境下确定其最优生产能力，它所面临的目标利润函数为

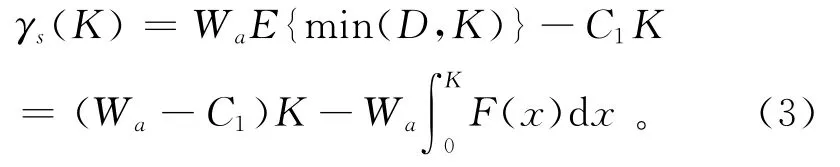
易得供应商选择在最优生产能力满足

此时购买商的期望利润为

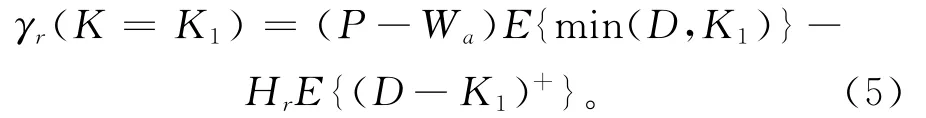
以上基本模型实际上是一个典型的报童问题，基本的假设条件和求解在文献［3－7］中都有相似描述。文献［13，16－18］从不同角度研究了供应链关系型契约，其基本的假设和基础模型也都来自于报童模型，下面将在报童问题的基础上提出本文的决策模型，并进行详细分析。尽管都借用了报童模型的基本假设，然而在新的供应链承诺契约设计环境下，供应链决策被赋予了新的管理含义。

2 引入订购量承诺契约时的决策模型

购买商希望能够采取措施影响供应商的决策，为此购买商承诺将保证向供应商购买一定的商品量，以此来降低供应商的能力设置风险。此时，供应商与购买商的竞争过程可以表述为：①购买商向供应商确定其承诺订购量χ；②供应商确定自己的生产能力K；③购买商观察到实际需求，向供应商确定最终订购量 max（χ，D）。

这里采用逆向归纳法来分析以上决策过程，预料到购买商将在第三阶段选择其最终订购量max｛χ，D｝，供应商面临的目标函数为

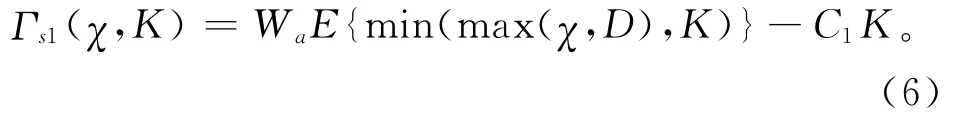
显然，K≥χ总是对供应商有利的，如果供应商认为购买商选择的承诺订购量总是小于其生产能力，则可得使供应商目标函数式（6）取最大值的生产能力为K1。综合分析可知，供应商的最优决策

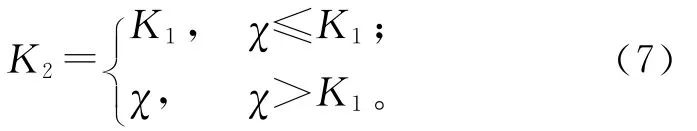
在第一阶段，购买商预料到供应商的反应函数后，需要确定其最优的承诺订购量，这里主要考虑以下决策情形：

（1）当χ≤K1时，购买商预料到供应商的最优生产能力设置为K1，故购买商没有必要选择正的承诺订购量，其最优承诺量必定为0，显然此时购买商的期望利润Γr1（χ＝0，K＝K1）＝γr（K＝K1）。

（2）当χ＞K1时，购买商预料到供应商的最优生产能力设置为χ，故购买商的目标函数为

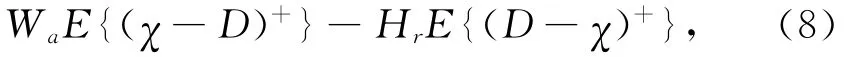
易得使购买商目标函数取最大值的生产能力χ1满足

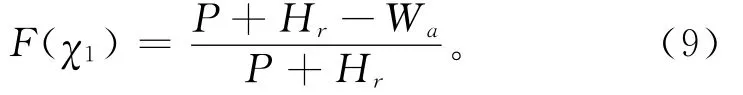
这里的约束条件χ1＞K1可以表示为

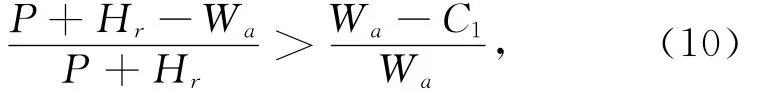
即

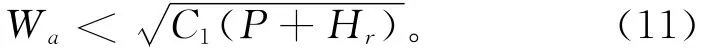
当式（11）成立时，购买商会通过比较期望利润的大小来确定其最终的决策。如果Γr1（χ＝0，K＝K1）≥Γr1（χ＝χ1，K＝χ1），则购买商选择的承诺订购量为0；如果Γr1（χ＝0，K＝K1）＜Γr1（χ＝χ1，K＝χ1），则购买商选择的承诺订购量为χ1。则购买商选择的承诺订购量总是为0。

在以上决策模型中，没有考虑批发价对供应链决策的影响。实际上，购买商对承诺订购量的决策受到批发价的影响很大，在不同的批发价取值条件下，供应链成员的决策也不同，订购量承诺契约对供应链的影响也不同。对购买商来说，如果批发价较高，则提前承诺需要承担的风险较高，因此购买商倾向于不进行订购量的承诺；相反，如果批发价相对较低，则购买商愿意通过一定量的承诺订购来提升自身的期望收益。因此，以上订购量承诺契约比较适合批发价相对较低的供应链契约。在实践中，供应商如果想要吸引购买商，就提前承诺订购较多数量的商品，而且必须要考虑降低批发价价格。下面的命题描述了适合于采用订购量承诺契约的批发价范围。

命题1 当批发价在区间（C1，P）内取不同的值时，一定存在着一个批发价区间，在该区间内，购买商一定会提前承诺订购量，并且相对于购买商未提前承诺订购量时的决策情形，供应链的性能实现了Pareto改进。如果式（11）不成立，即时，不等式

证明 显然，当总是成立。在竞争环境中，对零售商来讲，只有当下式成立时，才愿意进行提前订购量承诺：

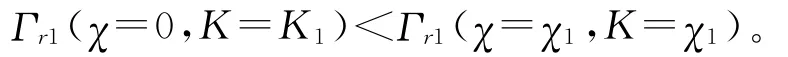
很显然，这里有

即函数Γr1（χ＝0，K ＝K1）在Wa＝C1时取值为－Hrμ，并开始递增，而函数Γr1（χ＝χ1，K＝χ1）在Wa＝C1时开始单调递减，当Wa＝P＋Hr时，有Γr1（χ＝χ1，K ＝χ1）＝－Hrμ。因此，一定存在着一个批发价区间⊂ （C1，W′a），使得购买商一定会提前承诺订购量，并且相对于未提前承诺订购量时的决策情形，购买商要获得更多的期望利润。当Γr1（χ＝0，K＝K1）＜Γr1（χ＝χ1，K＝χ1）成立时，必然有下式成立：

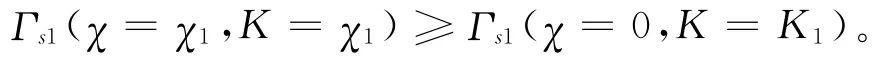
命题1表明，在区间（C1，P）内必然存在着一个区域，使得批发价落在该区域内时，购买商一定会提前承诺订购量，并且相对于购买商未提前承诺订购量时的决策情形，供应链的性能实现了Pareto改进。根据命题1，这样的Pareto区间存在于批发价相对较低时的决策情形，也比较符合实际情形，由于批发价相对较低，购买商提前承诺一定量的商品带来的成本相对较低，在面临缺货惩罚的条件下，购买商更有可能从提前承诺行为中获益。为下文分析方便，这里令Γt1（χ，K）＝Γs1（χ，K）＋Γr1（χ，K），代表供应链的整体收益水平。

3 基于订购量承诺的价格折扣策略

在有些供应链中，供应商有可能占据着一定的主导权，在销售季节开始前设置生产能力时，供应商会引入一定的诱导机制来吸引购买商进行订购量承诺。这里考虑供应商的诱导机制之一，即供应商决定为购买商的承诺订购量提供一个价格折扣α。另外，在调研中发现，购买商提前订购不一定都享受折扣，有时为了确保供应，购买商愿意以较高的价格购买商品。因此，为了将以上情形也包括在内，本文对折扣因子的约束定义为α≥0。为了方便，尽管当α＞1时购买商得到的是一个较高的承诺订购批发价，本文仍然将这样的情形称为折扣策略，并将α仍称为折扣因子。

这样的价格折扣机制在现实生产活动中也比较常见。由于购买商往往存在着多个可选的供应商，购买商习惯了在消除需求不确定之后向供应商订购确定量的商品。供应商为了吸引购买商尽早购买商品，以降低自身的库存风险，首先会采用的方法就是价格折扣机制。尤其是供应商面临多个购买商时，通过这种价格折扣策略可以吸引部分购买商抢先购买。另一方面，当供应商的商品非常畅销，而购买商之间存在着短缺博弈时，购买商为了确保供应，经常会用一个相对较高的价格向供应商提前承诺购买商品，同时要求供应商保证供应。

下面深入分析这样的价格折扣策略，研究供应链成员的最优决策，并且本文将主要考虑供应商占据主导者地位时的价格折扣机制。此时一个典型的竞争结构可以描述如下：

（1）供应商与购买商协商后决定引入价格折扣策略，即对购买商的承诺订购量，供应商必须提供一个价格折扣α，这里显然要满足αWa≥C1。

（2）购买商确定其承诺订购量χ。

（3）供应商根据购买商的承诺订购量，确定自己的生产能力K。

（4）购买商观察到实际需求，向供应商确定最终订购量。

这里仍然采用逆向归纳法来讨论以上竞争模型，在第四阶段，购买商的最终订购量显然为max（χ，D）。

在第三阶段，供应商在给定α和χ，并在预料到购买商的最终订购量后，确定自己的生产能力。此时，供应商的目标函数为

显然，K≥χ总是对供应商有利的，故式（12）可以表示为

如果供应商将χ看成总是小于K的常数时，易得

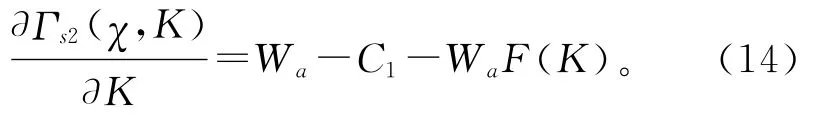
这样，供应商在第三阶段的最优决策如下：

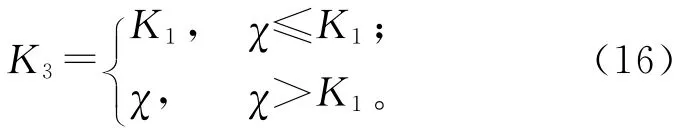
在第二阶段，购买商需要确定其最优的承诺订购量。购买商能够预料到供应商在第四阶段的反应函数。如果购买商认为其选择的承诺订购量总是满足χ≤K1，则供应商选择的生产能力保持为K1。因此，购买商的目标函数为

即有

得使购买商目标函数取最大值的承诺订购量χ2满足

显然，此时如果α≥1，则必然有χ2＝0。另一方面，如果购买商认为其选择的承诺订购量满足χ＞K1，则供应商选择的生产能力总是满足K＝χ。因此，购买商的目标函数为

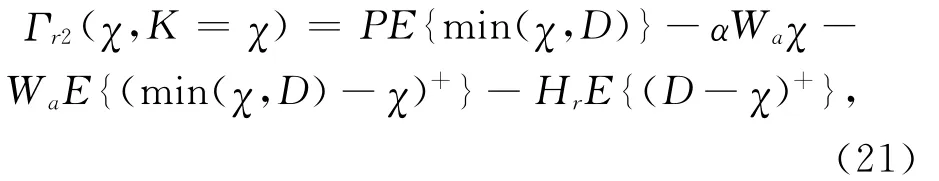
即有

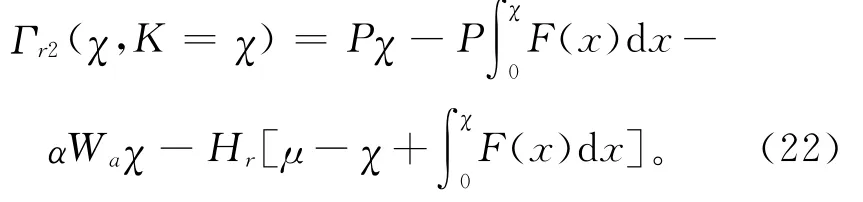
易得

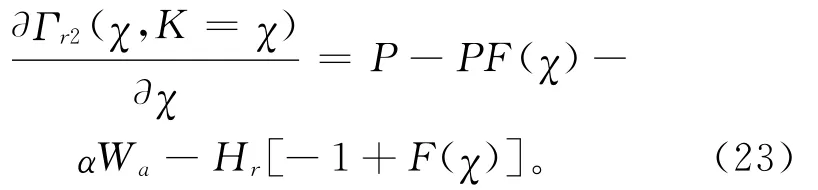
故使得购买商目标函数式（23）取最大值的承诺订购量χ3满足

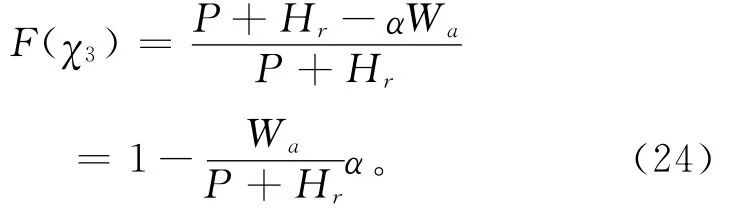
以上描述较好地分析了供应链成员在价格折扣策略下的决策模式，对供应链来说，必须在合适的区域内选择折扣因子，否则也会使供应链的整体性能降低。

命题2 当α≤α1时，会使供应链设置过多的生产能力，造成供应链整体性能失效。

证明 当α≤α1时，购买商选择的承诺订购量必然为χ3，供应商的生产能力也为χ3。而α≤α1成立时，总有成立，这样供应链提供的生产能力超过了供应链整体最优时的生产能力，即χ3≥Ka总是成立。这就造成了供应链过多地设置了生产能力，整体上失效了。因此，设置太低的折扣因子对供应链整体性能的改善是不利的。证毕。

根据命题2，从供应链整体性能来看，供应商选择数值较低的价格折扣是不合理的，会带来较大的购买商订购量增加，当供应量过多时，供应链的整体性能就失效了。在现实生产活动中，很多供应商为打开市场销路，吸引购买商采购更多的商品，往往会选择较低的价格折扣，最终可能会造成市场中商品的供应量过大。为了进一步确定折扣因子引入之后供应链成员的最优决策，给出以下命题。

命题3 一定存在唯一的一个折扣因子α＊∈（α1，α2），使得当α＜α＊时，购买商的最优承诺订购量为χ3；当α＊＜α≤α3时，购买商的最优承诺订购量为χ2；当α＝α＊时，购买商选择χ2或χ3将获得相等的期望利润。

证明 只需要确定α1＜α＜α2时购买商的决策问题。这里引入函数

有

另外，易得

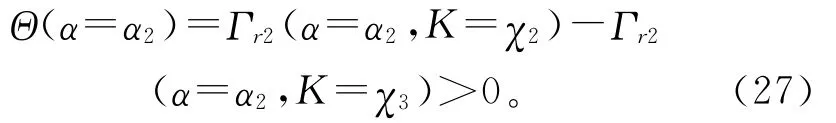
对任意的α∈（α1，α2），有

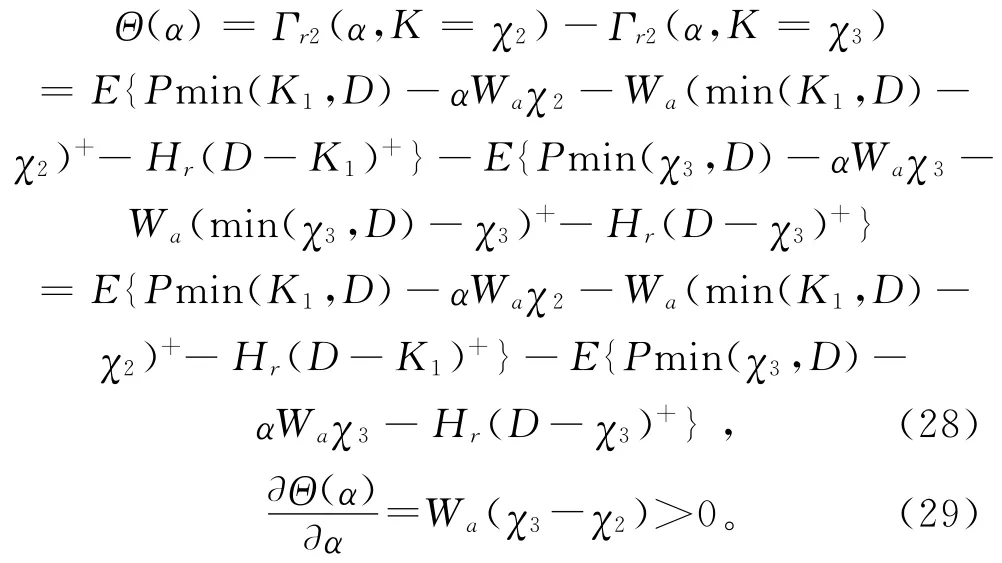
这样，函数Θ（α）在区间α∈［α1，α2］上连续、单调递增，又因为

所以此时一定存在唯一的一个折扣因子α＊∈（α1，α2），满足

证毕。

命题3很清楚地确定了购买商在价格折扣策略中的最优决策。可以看出，在价格策略中，不同的折扣因子会带来购买商不同的采购决策。该命题对供应商也有重要的参考价值，供应商应该认识到购买商的订购量承诺并不随着折扣因子连续波动，而是一个分段函数。因此，尽管有时供应商对折扣因子在一定范围内进行了调整，但是并不会影响购买商的承诺订购量决策。认识到这一点，合理规划自己的折扣策略对供应商来说就十分重要了。除此之外，购买商的最优决策还受其他交易参数，尤其是批发价格的影响。因此，在实际决策中，供应链成员必须综合考虑各个决策参数的取值，并据此确定自身的最优决策。

命题4 在价格折扣策略下，如果购买商选择的承诺订购量小于K1，则供应商没有动力提供价格折扣策略。

证明 供应商选择折扣因子时，如果预料到购买商选择的承诺订购量为χ2，供应商的最优生产能力为K1，则供应商面临的目标函数为

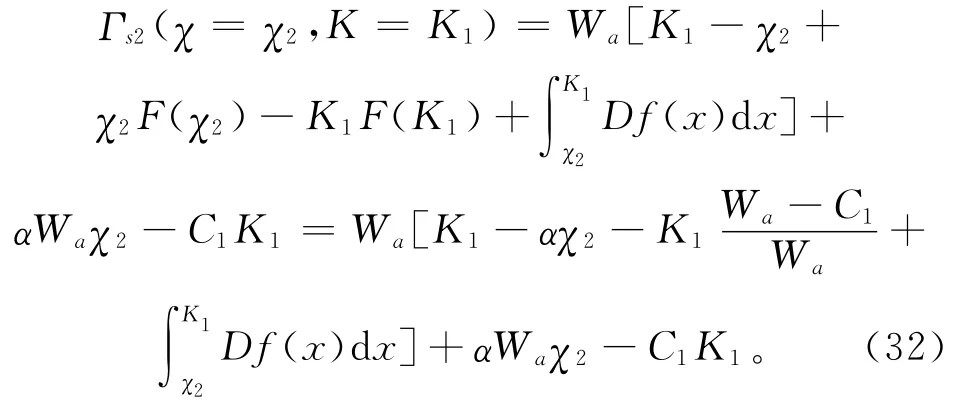
易得

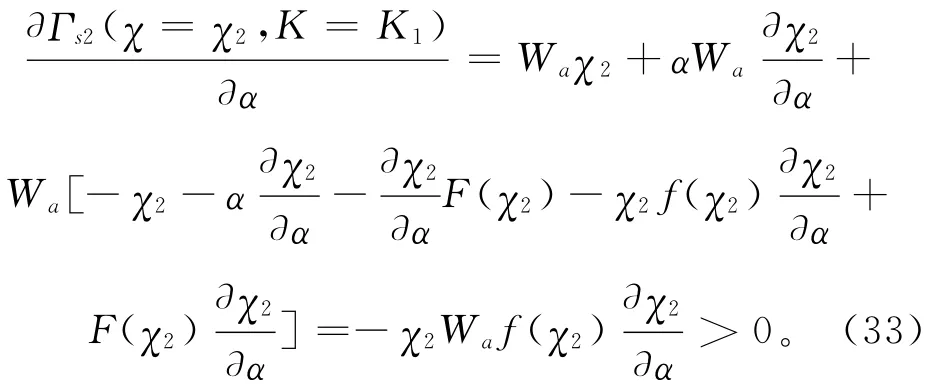
因此，价格策略如果是由供应商主导的，则供应商最佳的策略是不打折扣。证毕。

命题4是命题3的一个特殊情形，在这样的条件下，供应商并不能从折扣策略中得到任何好处，明智的决策是不打折扣。供应商选择折扣因子时，如果预料到“购买商选择的承诺订购量为χ3，供应商的最优生产能力为χ3”，则供应商面临的目标函数为

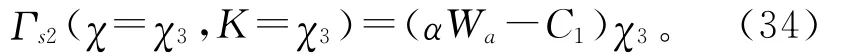
这里有

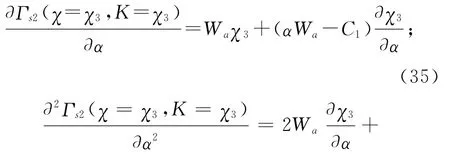
命题5 当α＊＞1时，相对于未引入价格折扣时的承诺契约，供应商一定能够通过引入价格折扣策略来提升自身的期望利润。

证明 由前面的讨论可知，当α＜α＊时，购买商的最优承诺订购量为χ3。另一方面，由式（34）所确定的供应商目标函数为折扣因子的凹函数。α＊＞1时，必然存在区间（1，α＊］，在该区间内选择折扣因子时，相对于未引入价格折扣时的承诺契约，供应商一定能够通过引入价格折扣策略来提升自身的期望利润。证毕。

根据命题5，如果购买商选择的承诺订购量为χ3，则相对于未引入价格折扣时的承诺契约，供应商存在着进一步提高期望利润的可能。只要α＊＞1，供应商就一定能够通过引入价格折扣策略来提升自身的期望利润。下文将通过数值算例来验证这一可能。

4 数值分析

令P＝20，C1＝8，Hr＝2。假设需求D 服从参数为λ＝1／200的指数分布，即该指数分布的概率密度函数可以表示为

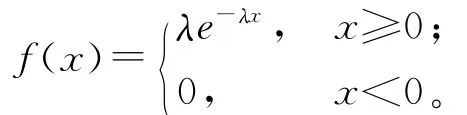
易得该需求随机变量的累积分布函数为

显然，该随机需求的均值μ＝200，这里首先考虑一个给定的批发价值Wa＝10，易得集成供应链选择的最优生产能力Ka＝202．320 2，集成供应链的最优期望利润γt（K＝Ka）＝781．437 8。在分散供应链中，供应商选择的最优生产能力K1＝44．628 7，供 应 商 的 期 望 利 润 γs（K ＝K1）＝42．970 4，购买商的期望利润γr（K＝K1）＝80。

现在购买商考虑引入订购量承诺契约，得χ1＝157．691 5＞K1。此时，供应商的生产能力K＝χ1＝157．691 5，供应商的期望利润Γs1（χ＝χ1，K＝χ1）＝315．383，购买商的期望利润为Γr1（χ＝χ1，K＝χ1）＝423．084 8。相对于未引入承诺契约时的决策情形，供应链的性能实现了Pareto改进。故在以上参数条件下，购买商会选择进行承诺订购，并且其最优的承诺订购量χ1＝157．691 5。根据命题1，适合引入订购量承诺契约的批发价约束条件C1＜Wa＜，即为8＜Wa＜13．266 5。

在区间Wa∈（8，13．266 5）内，总是满足χ1＞K1，存在着引入承诺契约的可能。图1所示为不同批发价情形下，引入订购量承诺契约前后购买商的期望利润变化。根据图1，当批发价落在区间Wa∈（8，11．345 0）内时，购买商总是乐意进行承诺订购，并且相对于未进行承诺订购时的情形，购买商将获得更多的期望利润。因此，在相对较低的批发价条件下，购买商能够从中受益，其承诺行为增加了供应链商品的总供应量。在给定批发价的情形下，如果购买商愿意进行提前订购承诺，并且其承诺量满足χ1＞K1，则这样的决策对供应商必然有利，供应商增加的期望利润为

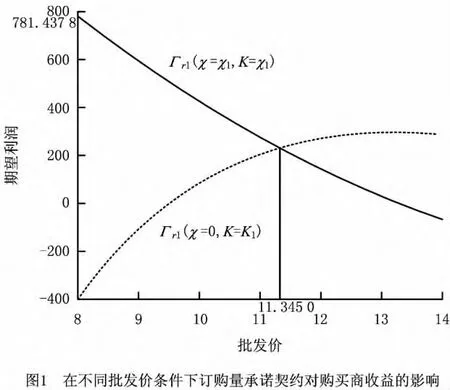
这样，当批发价落在区间Wa∈（8，11．345 0）内时，通过引入订购量承诺契约可以给供应链性能带来Pareto改进。显然，订购量承诺契约比较适合批发价相对较低时的供应链。因此，当以批发价为核心的供应链决策参数落在特定区域内时，完全可以通过引入承诺订购量来优化供应链的性能，并且能够实现供应链性能的Pareto改进。这是一个非常有趣的结论，其基本原理可以表述如下：当批发价相对较低时，单位产出带来的利润比较低，作为库存风险承担者的供应商会减少其生产能力设置，使得供应链的整体收益降低。这时，为了进一步提升供应链的性能，零售商必须要采取一定的措施来吸引供应商提高生产能力设置。根据前面的讨论，零售商通过承诺订购行为，降低了供应商的库存风险，增加了供应商的生产能力设置，并使得供应链性能实现了Pareto改进。

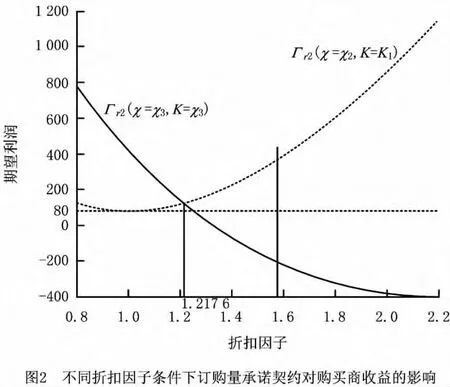
从图2中易得α＊＝1．217 6，当α在区间波动时，购买商将选择较少的承诺订购量，即χ2，相对于选择χ3时的情形，购买商将会得到更多的期望利润。由前面的计算可知，未引入承诺订购量折扣策略时，购买商的期望利润为γr（K＝K1）＝80；而引入承诺订购量折扣策略后，购买商总是能够通过选择恰当的承诺订购量来得到更多的期望利润。因此，购买商总是有动力引入承诺订购量折扣策略，来优化自身的期望利润水平。只要供应商提供价格折扣，购买商就一定会选择一个正的承诺订购量。

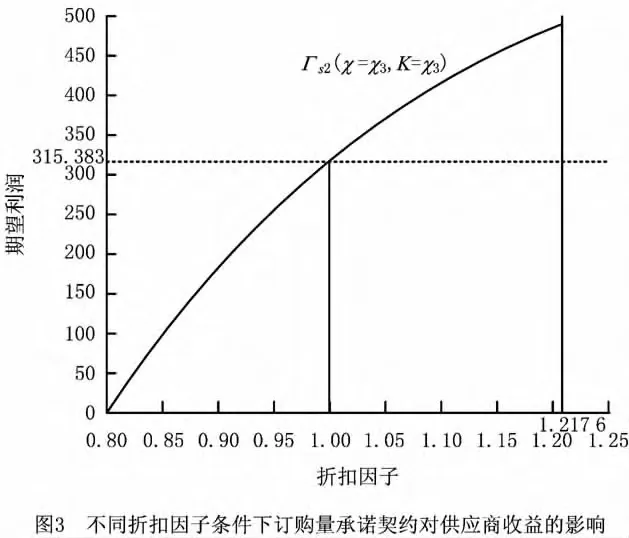
从供应商的角度来看，当α在区间［1，1．217 6］波动时，相对于没有引入价格折扣策略时的订购量承诺契约，供应商的期望利润又得到了进一步改进。供应商有动力采用价格折扣策略来影响供应链的决策。这是一个非常重要的研究结论。

以上数值分析较好地显示了在给定参数条件下供应链成员的最优决策，并且找出供应链性能改进的决策区间。从这些数值分析中可以看出，订购量承诺在供应链中的确能够起到一定的优化作用。如果供应商在竞争中占据主导者地位，则供应商有动力引入价格折扣机制，来进一步提升自身的期望利润。在实际应用中，有时价格折扣机制并不完全由供应商主导，购买商也经常通过自己的渠道权利来影响供应商的决策，并迫使供应商提供一个相对较低的折扣因子，以在将来获取较多的期望利润。供应商有时为了获取需求信息，或者提高市场覆盖率，不得不通过价格折扣的形式确保购买商的提前订购需求。

5 结束语

本文研究了一个不确定环境下的两级供应链模型，供应链由一个供应商和一个购买商组成。在传统运作模式中，供应商需要在不确定的环境下，确定其最优的生产能力设置，过多或过少的生产能力都将影响供应商的期望收益。本文考虑订购量承诺契约，通过事先确定订购量来改变供应链成员之间的竞争关系，寻找优化供应链性能的途径。本文的研究发现，在批发价相对较低的情形下，引入订购量承诺契约能够优化供应链的性能，实现供应链性能的Pareto改进。进一步研究了价格折扣策略对供应链性能的影响，并比较分析了不同折扣因子下供应链成员对最优决策选择的差异。运用丰富的数值分析对相关结论进行了说明，验证了订购量承诺契约在供应链管理的重要作用。今后的研究工作可以考虑存在多个供应链节点成员时的决策情形，并可以研究供应链成员间的信息不对称对供应链决策的影响。

［1］MANUJ I，MENTZER J T．Global supply chain risk management strategies［J］．International Journal of Physical Distribution ＆ Logistics Management，2008，38（3）：192－223．

［2］VEREECKE A， MUYLLE S．Performance improvement through supply chain collaboration in Europe［J］．International Journal of Operations ＆Production Management，2006，26（11）：1176－1198．

［3］LI Zheng，CHEN Xu．Manufacturer's optimal pricing policy and retailer's optimal ordering policy with capacity constraints［J］．Operations Research and Management Science，2012，21（5）：154－161（in Chinese）．［李 铮，陈 旭．考虑产能约束的制造商定价和零售商订货策略研究 ［J］．运筹与管理，2012，21（5）：154－161．］

［4］MENG Lingpeng，HAN Chuanfeng，WANG Jianmin，et al．Price Stackelberg competition and capacity constraints［J］．Chinese Journal of Management Science，2012，20（1）：139－144（in Chinese）．［孟令鹏，韩传峰，王剑敏，等．生产能力限制下价格Stackelberg博弈模型［J］．中国管理科学，2012，20（1）：139－144．］

［5］ZHANG Zili，LI Xiangyang，ZHANG Ziqiong．Emergency product production based on production capacity reserve［J］．Computer Integrated Manufacturing Systems，2009，15（7）：1349－1353（in Chinese）．［张自立，李向阳，张紫琼．基于生产能力储备的应急产品生产问题 ［J］．计算机集成制造系统，2009，15（7）：1349－1353．］

［6］SONG Xiaoqing，LU Zhimin，DONG Shaohua．Network capacity－based algorithm for short term production capacity planning problem in steel plant［J］．Computer Integrated Manufacturing Systems，2012，18（8）：1839－1844（in Chinese）．［宋肖青，吕志民，董绍华．基于网络能力的钢铁企业短期生产能力计划模型求解算法［J］．计算机集成制造系统，2012，18（8）：1839－1844．］

［7］CACHON G P．Supply chain coordination with contracts［M］／／Operations Research and Management Science：Supply Chain Management．Amsterdam，the Netherlands：Kluwer，2002．

［8］CAI Jianhu．Research on two－echelon supply chain inventory decision models for seasonal products［D］．Wuhan：Huazhong University of Science and Technology，2006（in Chinese）．［蔡建湖．季节性商品两级供应链库存决策模型研究［D］．武汉：华中科技大学，2006．］

［9］CHEN Zilin．A study on drop－shipping channel of supply chains under electronic business environment［D］．Wuhan：Huazhong University of Science and Technology，2008（in Chinese）．［陈子林．电子商务环境下的供应链drop－shipping渠道研究［D］．武汉：华中科技大学，2008．］

［10］LI Ming．Coordinate the drop－shipping supply chain with price－dependent stochastic demand［D］．Hefei：University of Science and Technology of China，2011（in Chinese）．［李明．考虑价格对需求影响的Drop－shipping供应链协调问题研究［D］．合肥：中国科学技术大学，2011．］

［11］TAYLOR T A，PLAMBECK E L．Simple relational contracts to motivate capacity investment：price only vs．price and quantity［J］．Manufacturing ＆Service Operations Management，2007，9（1）：94－113．

［12］MACAULAY S．Non－contractual relations in business：aprelim－inary study［J］．American Sociological Review，1963，28（1）：55－67．

［13］BAKER G，GIBBONS R，MURPHY K J．Relational contracts and the theory of the firm［J］．Quarterly Journal of E－conomics，2002，117（1）：34－84．

［14］SU Xuanming，ZHANG Fuqiang．Strategic customer behavior，commitment，and supply chain performance［J］．Management Science，2008，54（10）：1759－1773．

［15］HOFENK D，SCHIPPER R，SEMEIJN J，et al．The influence of contractual and relational factors on the effectiveness of third party logistics relationships［J］．Journal of Purchasing ＆Supply Management，2011，17（3）：167－175．

［16］DURANGO－COHEN E J，YANO C A．Supplier commitment and production decisions under a forecast－commitment contract［J］．Management Science，2006，52（1）：54－67．

［17］ANAND K，ANUPINDI R，BASSOK Y．Strategic inventories in vertical contracts ［J］．Management Science，2008，54（10）：1792－1804．

［18］CAI Jianhu，HAN Yi，ZHOU Gengui，et al．Inventory decision models of a two－echelon supply chain based on a commitment contract［J］．Systems Engineering—Theory ＆ Practice，2011，31（10）：1879－1891（in Chinese）．［蔡建湖，韩毅，周根贵，等．基于承诺契约的两级供应链库存决策模型［J］．系统工程理论与实践，2011，31（10）：1879－1891．］