烘丝机逆动力学过程模糊辨识

何 忠，雷 李，张 里

(1.重庆卷烟厂，重庆 400060;2.重庆理工大学电子信息与自动化学院，重庆 400054)

烘丝机是卷烟制丝工艺过程中最重要的工艺设备之一，其主要功能是对烟丝进行干燥，使其含水率符合一定的工艺要求，从而改善烟丝的弹性和填充能力，以提高烟丝的感官质量。烘后烟丝水分是直接影响卷烟内在质量的重要参数［1］。

烘丝机结构示意图如图1所示。烘丝机的工作原理是以饱和蒸汽为加热介质，为烘丝机滚筒筒体和热风提供热源，烟草叶丝跟随烘丝机筒体炒料板的翻炒进行热交换，从而达到叶丝干燥脱水目的［2］。由于烘丝过程是一类典型的涉及多变量、强耦合、时变、大滞后等多种因素的热工过程，难以建立精确的数学模型［3］，再由于烟草本身具有的特殊性质，从而使得烘丝过程的水分控制十分困难、复杂。

图1 烘丝机结构示意图

在卷烟生产过程中，由于卷烟牌号的不同可能要采用不同产地、不同品质的烟叶。在不同牌号卷烟的烘丝过程中，相关工艺参数需要进行试车、调整，一方面要耗费一定数量的烟丝原料，另一方面又要耗费较长的时间进行工艺参数的整定。

本文基于逆动力学辨识的思想，建立了基于某型滚筒式烘丝机的烘丝过程数学逆模型，为烘丝过程的工艺参数优化、提高烟丝水分控制精度奠定了基础，同时也为卷烟烘丝过程节能降耗，增加经济效益提供了一条可行的途径。

1 逆动力学过程模糊辨识基础

1.1 逆动力学模糊规则模型

根据系统的输出过程来确定导致此输出的输入过程是逆动力学方法的核心思想所在［4］。以SISO系统为例，若系统输入为u，输出为y，则可以采用 T－S结构［5］构建该系统的逆动力学过程模型:

模糊规则

自适应模糊推理

其中:z= 1，y[ ]TT为广义输入向量;n为模糊规则数量，仿真经验表明其取值一般不大于3。如果模糊规则的输入向量y(即系统的输出)落在球心为ci、半径为ri的广义球体内，则启采用第i条规则来求取系统的输入(即模糊规则的输出)中心ui。各权系数wi根据输入向量y与各局部区域中心ci之间的欧氏距离来计算［6］:

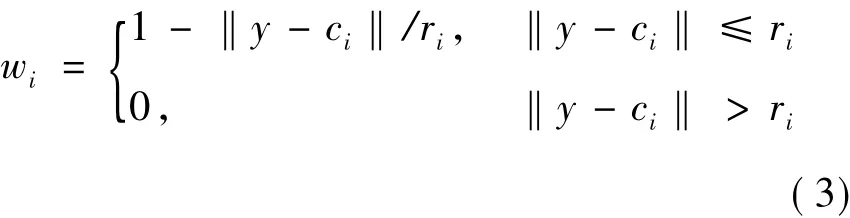
特别地，如果新输入数据没有落在训练样本输入区域的范围内，则通过与之距离最近的2个局部输入区域的模糊规则来进行计算，其权值wk和wh按下式计算:

且 i≠k。

逆动力学模糊规则模型的输入向量y应该结合具体应用背景来构造。一般分为2种情况:当通过已知的系统输出过程反求此输出的输入过程时，可以视为一种离线分析或诊断过程，其输入向量y采用下列结构即可:

而当需要进行在线实时控制时，即要求依据系统的期望输出过程来反演系统的输入过程时，输入向量y一般可按下述结构设计:

其中:u－ = [u(k－1)，u(k－2)，…，u(k－mu)]表示系统输入历史数据向量;y－=［y(k－1)，y(k－2)，…，y(k－my1)］表示系统输出的当前数据和历史数据向量;y+=［y(k+1)，y(k+2)，…，y(k+my2)］表示所期望的系统输出数据向量。

1.2 模糊规则的结构、参数辨识

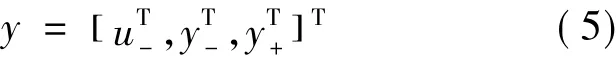
逆动力学模糊规则模型的建立需对模型的前后件的结构和参数进行辨识，即辨识各局部输入区域(ci，ri)及动态参数向量θi。在此引入熵的概念对输入空间进行初始聚类。对于维数为n的输入向量 y，按式(6)、式(7)［7］确定各样本的熵 Ej以及数据 yi和 yj之间的近似度 Si，j。

式中:σ为数据样本之间的平均距离;α=－ln(0.5/σ)。首先人工确定决策常数 β∈［0，1］，再以对应minEj的输入数据点yc1作为局部数据区域的初始中心c1，然后从输入向量y中剔除掉满足条件S(yj，c1)＞β的样本，再在剩余的样本集中确定区域的中心c2。依此类推，直至y为空集，可以确定初始局部输入区域的中心为C=(c1，c2，…，cn)。设定各区域的初始半径为r=0，i=1，…，n，采用竞争学习算法修正各区域中心及半径［8］。在获得的各局部输入区域(ci，ri)的基础上，任选择一组训练样本y(k)，u(k)，采用递推最小二乘法刷新各模糊规则的动态参数θi:

若‖y(k)－ ci‖≤ri，则:

若‖y(k)－ ci‖ ＞ ri，则［9］:

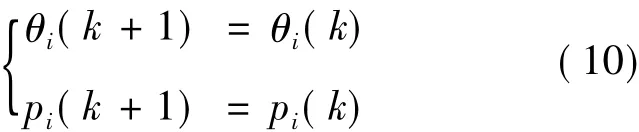
式中 λ 为遗忘因子，一般取值为［0.90，0.99］。递推初始时，取 θi=0，pi=αI，其中 I为单位矩阵;取α=105。

3 烘丝过程的逆模型辨识

烟丝烘丝过程是一个多输入多输出的MIMO系统，各种控制参数之间的耦合关系十分复杂，但经验表明，热风温度是对烟丝水分影响权值最高的控制参数，也是在实际生产中最主要的控制参数，故本文以某型烘丝机的现场生产数据为基础，基于逆动力学模糊规则建立热风温度与烟丝出口水分之间的关系模型。图2、3分别为某型烘丝机热风温度和烟丝出口水分的现场采样数据，采样周期均为5 s。

本文选择热风温度u(t－1)，u(t－2)以及烟丝出口水分y(t+4)，y(t+5)作为逆模糊规则模型的输入变量，模型输出为t时刻的热风温度u(t)。取前200组数据，经离线辨识得对象逆动力学过程初始模糊规则模型(局部输入区域数选择为2):

图2 热风温度变化曲线

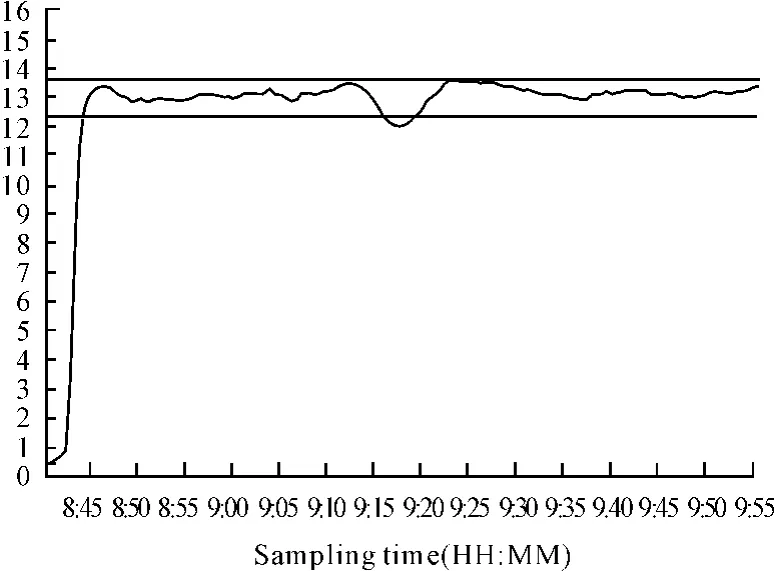
图3 烘丝机出口烟丝水分变化曲线

采用后200组数据进行在线辨识验证，即以后200点烘丝机出口水分采样值作为系统输入，在初始模糊规则模型的基础上，在线刷新模糊规则的动态参数θi，得到逆动力学模型的输出，记为um(k)，其与实际对应的热风温度值之差为▽u(k)=u(k)－um(k)，其结果如图4所示。

图4 烘丝机逆动力模型辨识结果误差变化曲线

4 结束语

本文基于逆动力学模糊辨识理论，以生产现场的实际采样数据为基础，建立了烘丝机出口烟丝水分与烘丝机热风温度的逆动力学模型。仿真结果表明:辨识结果具有较高的精度，误差峰值小于1%。而如何将逆动力学辨识应用于MIMO系统，实现多参数的系统辨识将是值得继续探讨的课题。

利用系统的输出要求反演系统的控制输入是逆动力学辨识应用于控制的思想内核。烘丝机工艺参数的优化及控制效率的提高具有巨大的经济和社会效益。将逆动力学辨识的思想应用于烘丝机控制无疑为烟草行业工艺过程的优化开辟了一条值得期待的途径。

［1］王艳红，韩光胜.烟草烘丝过程的水分控制［J］.北京工业大学学报:自然科学版，2000，26(4):90－95.

［2］饶琳，陈良元，席年生.分段式低温滚筒叶丝干燥设备研究［J］.新技术新工艺，2009(10):95－97.

［3］王广军，何祖威，陈红.基于神经网络和过程机理特性的锅炉蒸发系统仿真［J］.中国电机工程学报，2001，21(11):65－68.

［4］邓良才，王广军，陈红.锅炉汽温对象的在线模糊辨识［J］.中国电机工程学报，2006，26(9):111 －115.

［5］Takagi T，Sugeno M.Fuzzy identification of systems and its applications to mod eling and control［J］.IEEE Trans Syst，1985，15(1):116 －130.

［6］岳玉芳，毛剑琴.一种基于T－S模型的快速自适应建模方法［J］.控制与决策，2002，17(2):155 －158.

［7］黄艳新，周春光，杨国慧，等.基于熵聚类模糊神经网络味觉信号识别系统的研究［J］.计算机研究与发展，2004，4l(3):414 －419.

［8］吕剑虹，陈建勤，刘志远，等.基于模糊规则的热工过程非线性模型的研究［J］.中国电机工程学报，2002，22(11):132－137.

［9］王广军，朱丽娜，沈曙光.一种基于逆动力学模糊规则的自适应控制方法［J］.系统仿真学报，2008，20(15):3907－3910.