离散元法侵彻混凝土靶板数值模拟研究

吴东旭，姚 勇，刘筱玲，邓勇军

(西南科技大学土木工程与建筑学院，四川绵阳 621000)

早期，人们对于侵彻混凝土过程的模拟均是基于连续介质理论分析的力学行为，即假设混凝土为各向同性材料。然而，混凝土是由砂浆和骨料以及其他一些材料组成的非均质复合材料［1－2］。PFC3D(particle flow code in three dimension)即三维颗粒流程序［3］，将模拟分解为成千上万的颗粒来研究，通过离散单元法(discrete element method)模拟球形颗粒的运动和颗粒之间的相互作用。颗粒之间的相互作用有2种方式，即接触键粘结和平行键粘结。由于当前的目标是模拟一种摩擦－粘结材料的混凝土，而前人对混凝土的研究分析表明平行粘结可以模拟接触的2个颗粒之间的接触力和力矩［4－5］，所以本文采用平行粘结来建立数值模型。

通过对混凝土单轴压缩/拉伸的数值仿真［6］，标定混凝土在准静态条件下的弹性性质和强度性质的离散元细观力学参数。对混凝土在弹丸侵彻下的试验进行数值模拟研究，模拟不同弹丸速度下混凝土的动态力学响应，分析混凝土的非均质性对弹丸剩余速度和偏转角的影响。

1 Hanchak侵彻试验介绍

试验中靶板的尺寸及靶体中的钢筋分布位置如图1所示。靶板混凝土的单轴抗压强度为48 MPa，混凝土中的最大骨料粒径为9.5 mm，骨料莫氏硬度为 6.6。

由于Hanchak侵彻试验［7］时弹头冲击靶板正中央不接触钢筋，弹体侵彻后的残余速度受钢筋影响很小［8］，所以本文建立的靶板数值模型中没有考虑钢筋的作用。

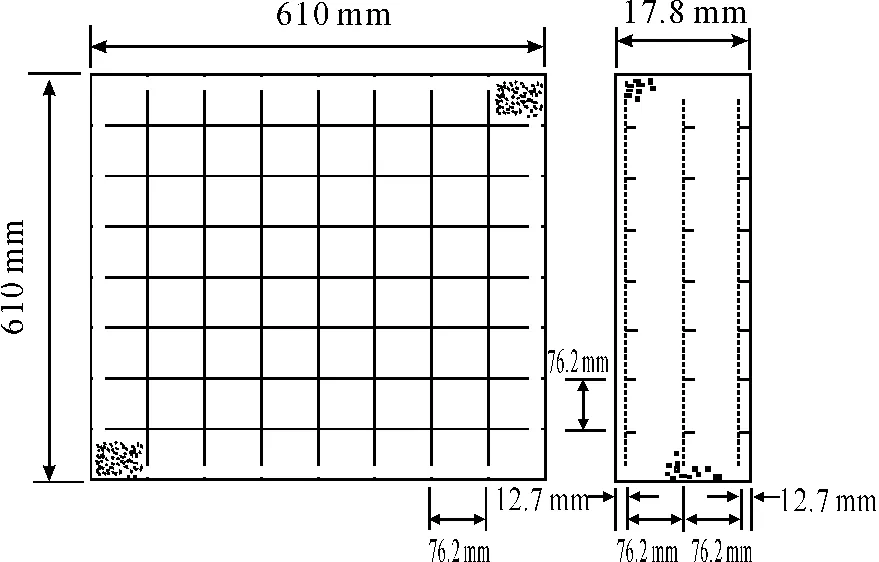
图1 靶板几何尺寸

图2 子弹几何尺寸

2 单轴压缩/拉伸数值仿真

PFC3D的基本单元是球形颗粒，混凝土靶板的离散元模型就是一系列离散的球形颗粒的集合。对于每一个球形颗粒都必须分配一套局部的细观参数，使得这个集合的宏观行为能反映真实的模型。目前，对于混凝土而言，细观参数的获取方法就是基于准静态单轴压缩/拉伸试验的仿真。

通过试验，得到了局部参数 kn，ks，pb_kn，pb_ks，pb_nstrength，pb_sstrength，使得球形颗粒集合的力学性能与杨氏模量为34 GPa和抗压强度为48 MPa(见图3)的混凝土尽可能接近。混凝土的离散元细观力学参数见表1。

表1 混凝土离散元细观力学参数

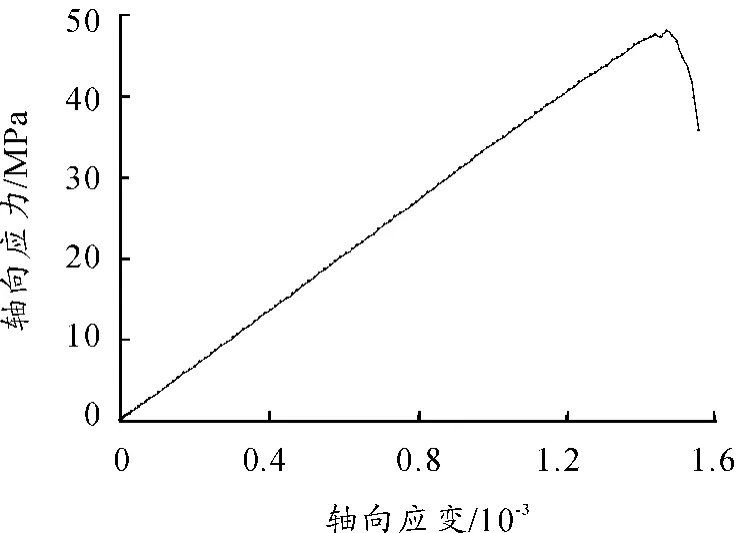
图3 混凝土单轴压缩时的应力应变关系

3 混凝土靶板和弹体模型

靶板的尺寸选取是基于Hanchak试验的混凝土靶板确定的，即610 mm×610 mm×178 mm。在PFC3D内嵌FISH函数的控制下，生成混凝土靶板的模型，并通过循环去除初始应力，如图5所示。靶板中离散元颗粒的总数为26 436，半径在0.005 m到0.01 m范围内。混凝土靶板中球形颗粒的大小是根据准静态压缩/拉伸试验模拟中的颗粒粒径确定的。

通过循环的多次调用，生成Hanchak试验中所用到的尖卵形弹头的弹丸(crh=3，见图2)，弹丸直径为12.7 mm，长度为143.7 mm，如图 4所示。试验一般假定弹体是刚性的，所以在离散元模型的参数中，弹体刚度的取值应比靶板的取值稍大。PFC3D中的Clump Logic允许用户生成自定义的超级颗粒。超级颗粒由许多基本的球形颗粒组成，具有不变形的边界条件，而且计算过程中超级颗粒的内部颗粒之间接触力不予考虑，因此可以把超级颗粒当成一个刚体。用这样的超级颗粒来近似模拟刚性弹体是最合适的。

图4 弹丸离散元模型

图5 靶板离散元模型

4 计算结果与分析

为了有效地提高计算效率，初始状态下，弹体建立在靶板的正上方，距离靶板很小的垂直距离，如图6所示。在弹体上施加不同的初速度，对不同弹丸速度侵彻混凝土靶板进行数值模拟研究。离散元法对动态的模拟需要设置合适的时间步Δt，计算时间步的选取必须满足以下条件:

其中:m是所有颗粒的质量总和;k是所有颗粒刚度的总和。理论证明:当根据公式选取离散元法的计算时间步时，解一般是收敛的，可得到可靠解［9］。

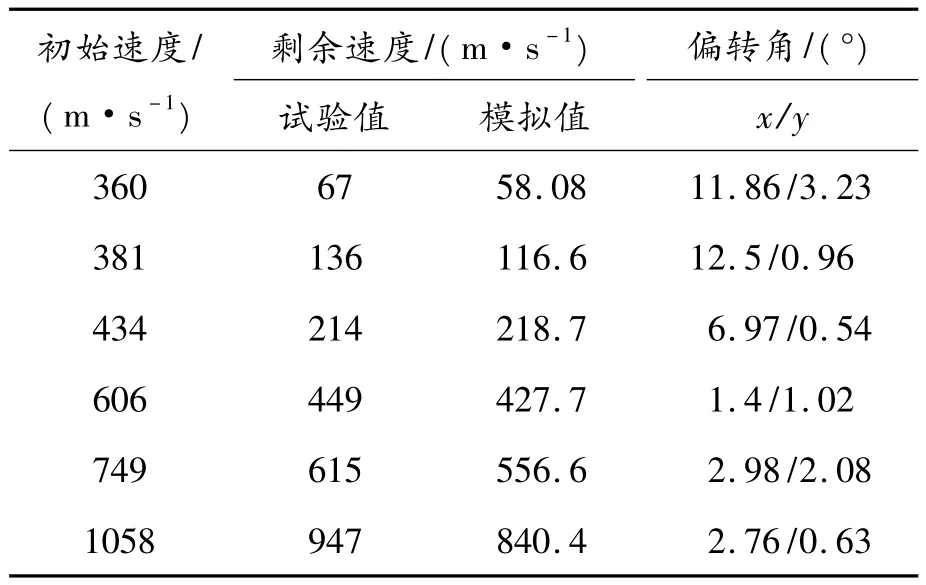
表2 弹丸剩余速度和偏转角

图7是弹丸穿透混凝土靶板的情形。通过图7与图6的对比可以看出:混凝土上表面具有一定程度的开坑，下表面也有一些被打散的混凝土颗粒飞溅的过程，这与实际情况相符。图8、9分别是初始速度为434 m/s时的弹丸速度和加速度时程曲线。弹丸以不同初始速度侵彻混凝土靶板时的剩余速度和偏转角见表2。从表2可以看出:弹丸剩余速度模拟值与试验值非常吻合，相对误差在15%范围内，与用连续有限元法考虑混凝土的多项组成时得到的结果也是比较吻合的［10］。

图7 弹丸穿透混凝土靶板

图10是弹丸以434 m/s的速度侵彻混凝土靶板时，弹丸在xy平面内的偏转角随时间的变化关系。由于混凝土具有多项非均质性，弹丸在侵彻过程中的偏转角是不停变化的。从表2可以看出:弹丸出靶时的偏转角与侵彻的速度有关，较大的侵彻速度得到的偏转角较小。这表明速度越大，混凝土的均质性越强。也就是说，当速度达到某一个临界值时，混凝土也可以当做均质的材料来处理。从数值模拟的结果可以得出:初始速度在600 m/s以上时，偏转角已经很小，即侵彻速度在600 m/s以上时，混凝土的非均质性可以不予考虑，此时将混凝土考虑成均质的连续介质是可行的。

图8 弹丸的速度时程曲线

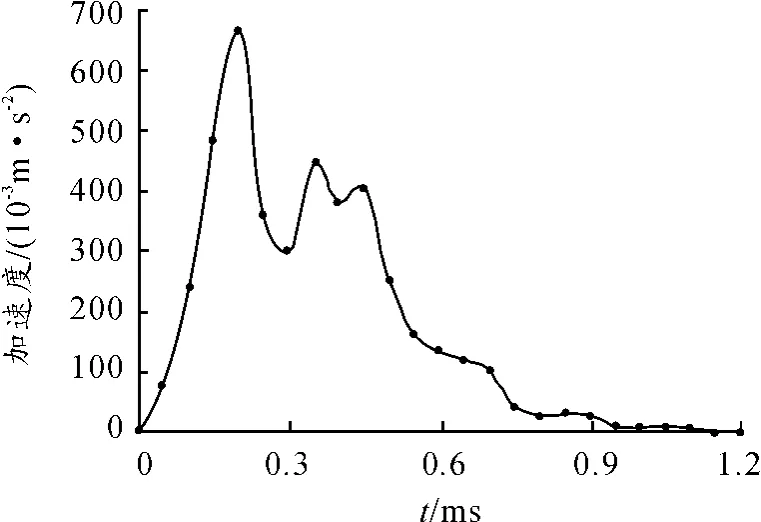
图9 弹丸的加速度时程曲线

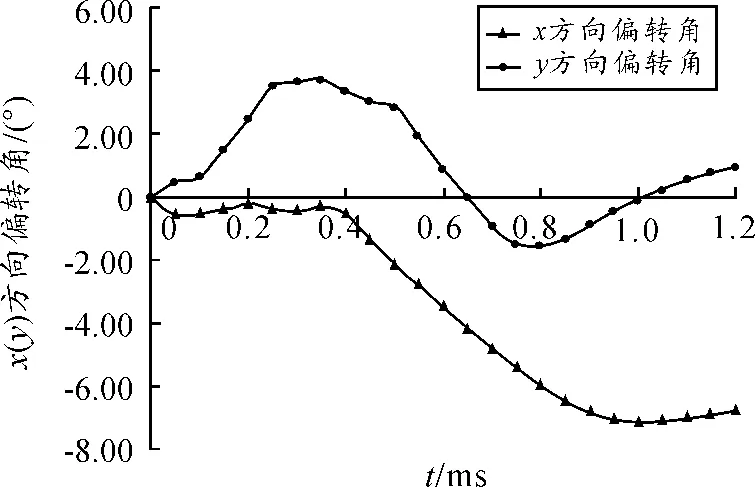
图10 弹丸的偏转角随时间的变化关系

5 结论

1)准静态的单轴压缩/拉伸试验再现了混凝土的准静态力学行为，是获取混凝土的离散元细观力学参数的关键。

2)采用离散元法模拟弹丸侵彻混凝土靶板，弹丸穿透混凝土的剩余速度与试验数据吻合，且能再现混凝土被破坏时的颗粒飞溅现象。

3)偏转角是衡量混凝土材料均质性的标准，较大的初始速度使得弹丸出靶时的偏转角较小，说明在初始速度很大的情况下，将混凝土考虑成均质的材料来处理是合理的。

［1］姜华，王君杰.弹体侵彻混凝土数值模拟失效指标研究［J］.振动与冲击，2009，28(8):30.

［2］郭香华，张庆明，何远航.混凝土厚靶在弹体正侵彻下的响应研究［J］.北京理工大学学报，2011，7(31):765－767.

［3］CUNDALL P A，STRACK O D L.A discrete numerical method for granular assemblies［J］.Geotechnique，1979，29(1):47－65.

［4］WANG Zhuolin，LIN Feng，GU Xianglin.Numerical Simulation of Failure Process of Concrete Under Compression Based of Mesoscopic Discrete Element Model［J］.SCIENCE AND TECHNOLOGY，2008，67(4):19 －25.

［5］Donzé F V，Magnier S A，Daudeville L，et al.Numerical study of compressive behavior of concrete at high strain rates［J］.Eng Mech，1999，125(10):1154 －1163.

［6］Hentz S，Daudeville L，Donzé F V.Identification and validation of a discrete element model for concrete［J］.Eng Mech，2004，130(6):709 －719.

［7］Hanchak SJ，Forrestal MJ，Young ER，et al.Perforation of concrete slabs with 48 MPa and 140 MPa unconfined compressive strengths［J］.International Journal of Impact Engineering，1992，12(1):1 －7.

［8］Holmqust T J，Johnson G R，Cook W H.A computational constitutive model for concrete subjected to large strains，high strain rates and high pressures［C］//Proceedings of the 14th International Symposium on Ballistics.Canada:［s.n.］，1993:591 －600.

［9］魏龙海，王明年，陈春光.三维离散元模型及计算参数选取研究［J］，重庆交通大学学报，2008，27(4):615－621.

［10］赵睿，姚勇，邓勇军.K＆C模型的随机骨料混凝土侵彻应用［J］.四川兵工学报，2013，31(1):105 －107.