不对称刚度支撑致横向振动柔性夹具试验

王 飞，杜 强，刘剑钊，万方美

(中国工程物理研究院总体工程研究所，四川绵阳 621900)

在一般振动试验中，振动夹具的设计一般遵循刚性设计原则［1］，即在设计条件允许的情况下，夹具设计刚度应尽可能的高，以提高夹具的一阶共振频率，避免给定环境试验条件下共振现象的发生，并限定允许的正交运动，即规定在非试验方向的振动值必须小于某个值，也就是限定各种横向运动。然而，由于并不存在理想的刚性夹具，且夹具与试件的转接界面也会对系统刚度造成影响［2］，从而产生非线性系统［3－6］。因此，只能在设计允许的条件下尽量进行控制。

在实际工程应用中，针对某特殊产品器件的振动环境适应性考核，载荷输入中必须包含与主振向具有一定相差的横向振动载荷，以使器件得到更全面的考核。为获得该类载荷，可直接使用多轴振动台进行驱动。目前，国内外均已成功开发了多轴振动试验系统，主要分为电液式和电动式两类［4］:电液式振动台结构简单、技术成熟、推力大、成本低，但驱动频率较低，一般为0～100 Hz;电动式多轴振动台一般由标准电动振动台组合而成，试验频率可达5～2 000 Hz，但由于各向运动解耦控制困难，有效载荷相对较低。在多轴振动台不能满足特殊载荷要求的情况下，本文采用柔性夹具设计［5］，以获得特定的输入载荷。

柔性夹具是通过结构动力学优化，按照动力学特性指标开展设计，使所获得的环境振动试验条件满足使用要求。根据不同刚度斜向支撑的柔性夹具设计思路，将不同方向的振动进行耦合，以在单轴振动台上产生特定的横向载荷用于产品的工程考核。

1 柔性夹具设计原理

对于本文所涉及的特定载荷问题，主振向(轴向)载荷与横向载荷无相差或完全反相(相差180°)是没有工程意义的，因为此时2向振动效应会线性叠加，形成单向振动效应，无法满足特定的考核要求。

在单轴振动台的激励条件下，柔性夹具的动力学设计的主要设计思路为:将振动台面的单轴振动输入(ys)通过2斜向以不同刚度(k1，k2)和阻尼(c1，c2)进行支撑。在这种情况下，2斜向支撑传递函数的差异将导致质量块(m)2斜向振动响应在特定频率范围内存在相差，从而实现所需要的振动载荷形式。夹具的动力学设计简化模型如图1所示。响应质量块通过铰链模型在2个斜向(45°)与振动台相连，即非对称刚度支撑。

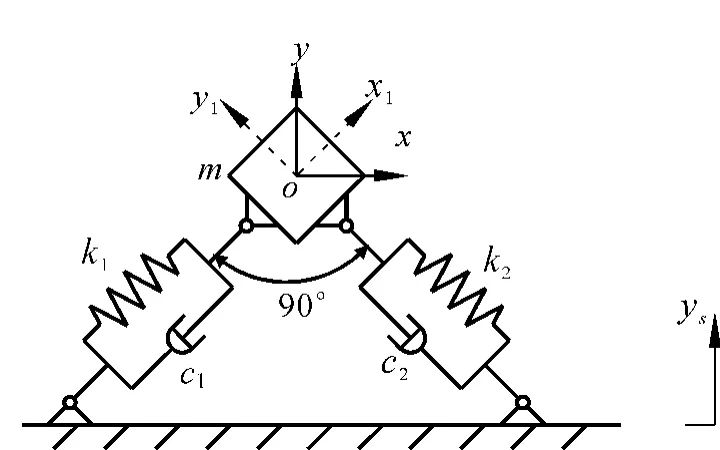
图1 非对称刚度支撑柔性夹具动力学设计模型

基于此模型，对响应质量m的振动响应求解如下:首先建立响应质量块主振向－横向运动坐标系(x，y)与2斜向支撑方向运动坐标系(x1，y1)的关系如式(1)所示。

同时，设振动台面的支承运动为

在不考虑重力的情况下(重力仅影响系统平衡位置)，建立响应质量在坐标系(x1，y1)下的振动微分方程为:

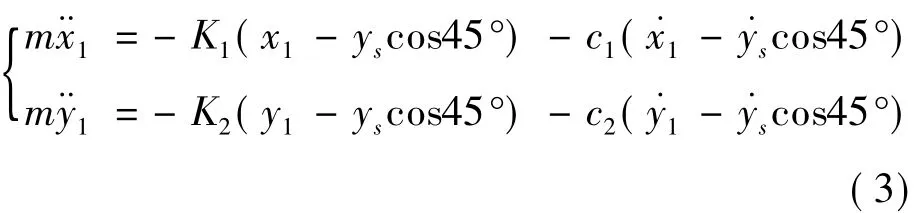
根据式(3)可求得x1向振动的复数形式为

其中:

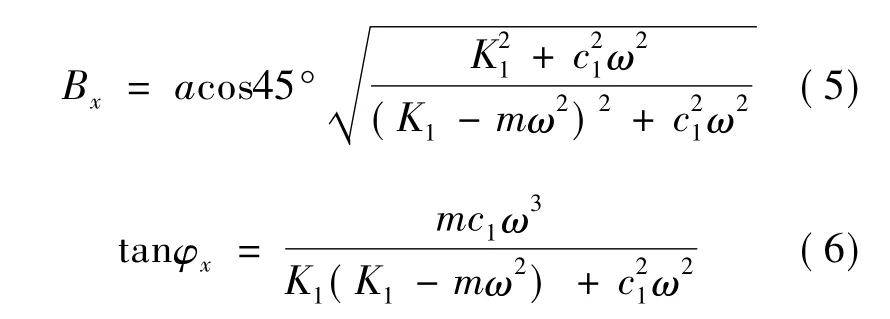
同理，y1向振动方程具有类似表达形式，给出

其中:

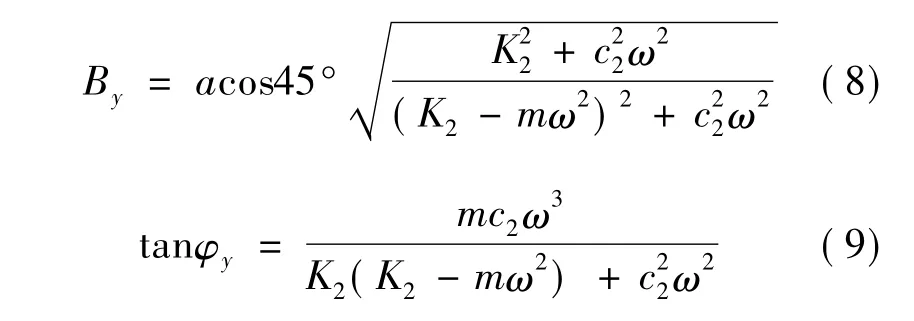
从试验件在x1，y1两向的振动方程可以看出:在此简化动力学模型下，2个方向形成了独立的强迫振动响应，且响应频率与输入频率一致，但由于刚度和阻尼的差异，2向响应具有一定相差。将求解出的响应代入式(1)即可求得质量块在主振向和横向的振动响应。

给出该非对称刚度支撑柔性夹具设计模型下的主振向(y)及横向(x)的典型响应特性曲线如图2所示。图中，横坐标为激振频率与夹具的一阶共振频率(弱刚度斜支撑向共振频率)的比(λ)。从图2可以看出:频响曲线为典型的二阶响应形式。在低于系统一阶频率的频率段，振动响应以主振向为主，且2向振动基本无相差;在一阶频率与二阶频率之间，横向振动强度大于主振向，且具有一定相差;在高于二阶频率的范围内，2向振动幅值相当，且相差约为π。据此，满足设计使用要求的频率区间为2共振频率之间的频率范围。

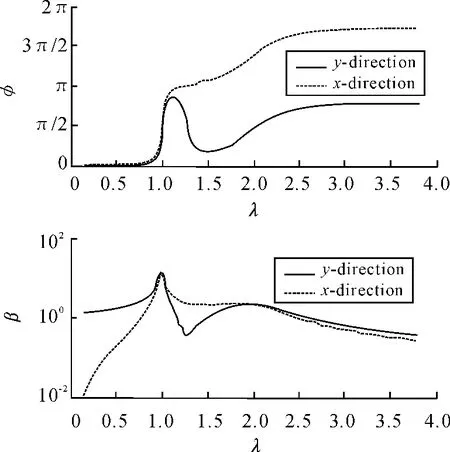
图2 非对称刚度支撑柔性夹具频响曲线

2 柔性夹具工程设计及模态分析

2.1 工程实现

由于理想的铰链结构在工程应用中难以实现，因此在实际设计中，采用了夹胶U形板簧斜向支撑结构，如图3所示，通过选择钢制板簧的厚度来获得不同的支撑刚度。另外，由于结构阻尼是产生响应相差的关键，因此在U形板簧内腔完全填充阻尼材料，并通过填充材料的选择来获得不同的结构阻尼。

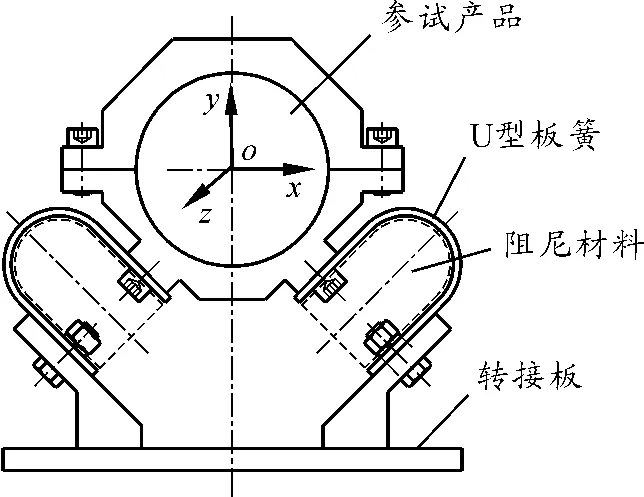
图3 柔性夹具工程设计示意

2.2 模态有限元分析

使用Abaqus软件进行柔性夹具的结构建模，完成模态分析结果如图4所示。

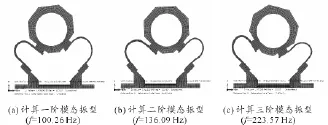
图4 柔性夹具模态有限元分析结果

由于阻尼填充材料的弹性模量相对较小，对板簧刚度的影响有限，主要起阻尼耗能作用，因此为简化模型、提高计算效率，将非线性阻尼填充层的阻尼效应简化为各阶模态的阻尼系数，而不在几何模型中体现。从分析结果可以看出:一阶模态主要体现为薄U形板簧的斜振向;二阶模态主要体现为厚U形板簧的斜振向;三阶模态为平面转动向。区别于夹具的动力学设计简化模型，板簧与底座及响应质量之间采用螺纹固接而不是铰链连接，因此存在转动形式的第三阶模态。

此外，计算所得的第四阶频率为1 251 Hz，远高于前三阶频率，因此前三阶模态将主要决定夹具的动态特性。模态分析结果表明:非对称支撑柔性夹具的低阶模态中，存在明显的横向振动形式。

3 柔性夹具振动试验

3.1 模态试验

对加工完成的振动夹具，采用锤击法进行模态试验分析，测试结果如图5所示。测试一阶模态体现为绕x轴的扭摆振型，在有限元分析中采用的平面二维分析无法分析出此种振型;测试二阶模态与有限元分析结果相吻合，体现为板簧的压缩振型;测试三阶模态振型与有限元分析结果一致，体现为绕z轴的转动振型。由于连接为螺纹连接，连接刚度低于有限元分析中所采用的固连模型，因此共振频率略低于有限元分析结果。此外，在模态试验中，软件程序并不能识别出有限元分析得到的一阶模态振型，而模态分析只是为了获得振动特征参数，不会对柔性夹具的振动特性产生影响，因此本文不深入讨论此问题。

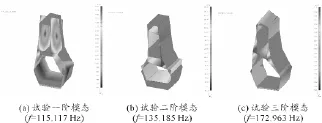
图5 柔性夹具模态试验分析测试结果

3.2 正弦扫频试验

在单轴振动台上完成的柔性夹具的振动测试试验现场如图6所示，给出夹具上方测点的主振向与横向的频响曲线如图7所示。从结果可以看出:该柔性夹具在单轴振动台上具有显著的横向响应，且横向响应为典型的二阶双峰响应形式，在2响应峰之间的频率范围内，与主振向响应具有不同的相差，这与图2所示的设计相吻合，满足了夹具的预期使用要求。值得一提的是，在二阶频率峰附近，横向振动量级大于主振型响应，因此，基于非对称刚度支撑致横向振动的柔性夹具设计达到了预期目的。

同时，我们也注意到:与图2的设计频响曲线相比，实际曲线形式更为复杂，特别是主振向响应并没有体现出显著的多阶形式，表面振动台能量输入仍主要体现在主振向方向，横向振动分量在较大频率范围内仍为小量。分析其原因在于:U型板簧在工程实践中采用了螺纹紧固装配，而不是设计中理想的无转动约束的铰链结构，因而导致横向运动自由度受到了一定约束，使振动能量输入有限。

图6 振动试验现场图

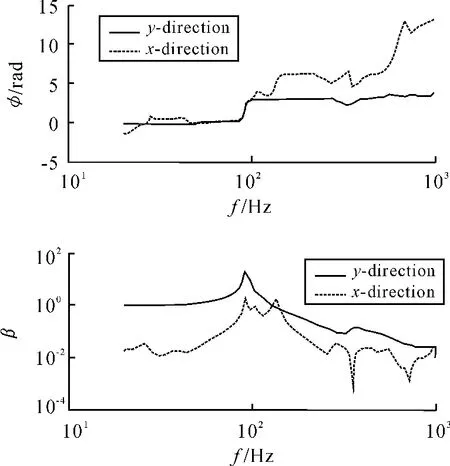
图7 柔性夹具实测频响曲线

4 结束语

由于某产品器件振动环境的适应性考核需要一定量级横向振动的设计要求，本文提出了2斜向不对称刚度支撑致横向振动的柔性夹具设计思路，并基于此完成了设计分析及试验。试验结果表明:夹具在横向产生了明显的振动分量，且在特定的频率范围内，横向振动量级幅值大于主振向。通过不同刚度、阻尼组合的系列化设计，即可实现在不同频段上具有显著横向振动的夹具形式。同时，在试验中也发现:在绝大部分频率范围内，主振向振动仍占主导地位，与简化模型的动力学分析预测存在一定差异，其主要原因是在工程设计中无法采用无转动约束的铰链结构。此外，阻尼灌封层的材料除了主要提供结构阻尼之外，还会影响U形板簧的刚度及变形状态，对设计预期带来影响。

［1］胡志强.随机振动试验应用技术［M］.北京:中国计量出版社，1996.

［2］Matthew S A，Harrison M Gindlin，Randall L M.Experimentalmodalsubstructuringtoestimatefixed-basemodes from testsonaflexiblefixture［J］.Journal of Sound and Vibration 2011，330:4413 －4428.

［3］孔宪仁，廖俊，杨正贤.随机激励下非线性振动系统特性的定性分析［J］.航天器环境工程，2010，4:462－467.

［4］夏益霖.多轴振动环境试验的技术、设备和应用［J］.导弹与航天运载技术，1996，6:52－59.

［5］顾松年，姜节胜，周苏枫.柔性夹具与环境振动试验［J］.机械强度，2003，25(2):119 －122.

［6］张建，张汉伟，盛德兵.发射装置中振动控制点选择方法分析［J］.重庆理工大学学报:自然科学版，2012，26(12):40－46.