振荡积分的数值计算与Matlab实现

陈卫红

（安徽财贸职业学院，安徽 合肥230601）

振荡积分的数值计算与Matlab实现

陈卫红

（安徽财贸职业学院，安徽 合肥230601）

本文提出利用样条函数计算及类型的振荡积分，在每个比较小的子区间采用分部积分法，避免了整体利用分部积分需要计算函数在区间端点处的高阶导数，能提高计算的精确度.

振荡积分；样条插值；Matlab实现

1 背景导引

2 积分计算原理分析

设f(x)的样条插值函数为S(x)，则

首先，将积分区间[a,b]n等分，h=(b-a)/n，结点坐标为xi=a+ih(i=0,1,…,n)

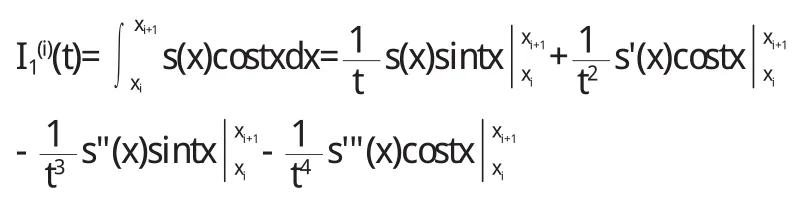
由于在每一个区间上的s(x)为三次多项式，因此s'"(x)为一常数，且在子区间[xi,xi+1]上

令s"(xi)=Ti则有s'(x0)=s'(a)=f'(a)，s'(xn)=s'(b)=f'(b)

于是有

利用类似方法得到

如果积分区间为[0,2π]，则上述两个公式就变为

如果等分数n能除尽t，则上述两个公式又可化简为

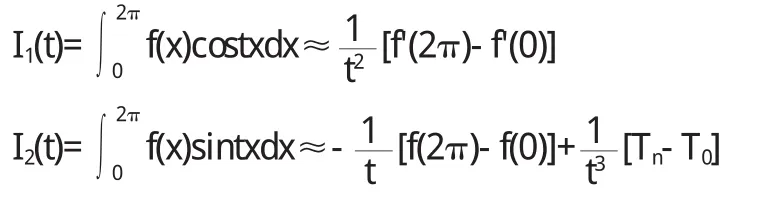
3 Matlab实现

利用Matlab自编T文件或它自带的样条插值计算工具箱算得T0=-1.73908T3=-6.80476

一般来说，用样条函数来处理振荡积分能大大提高精确度．

〔1〕孙志忠.数值分析[M]．南京：东南大学出版社，2002．

〔2〕张德荣.计算方法与算法语言[M]．北京：高等教育出版社，1981.

O246

A

1673-260X（2013）12-0004-01