一种关键线路和重要保护辨识的新方法

周 亮，陈定辉，陈庆芳，张 琼，张海翔，吕飞鹏

((1.西昌电业局，四川 西昌615000;2.四川大学 电气信息学院，四川 成都610065)

0 引 言

随着电力系统的快速发展，电网逐渐形成跨区域、大规模、多环网的现代互联电网，这种现代互联电网对电力系统的安全可靠性提出了严峻的挑战。近年来，各国发生多起大停电事故［1～3］造成了巨大的经济损失和社会影响，这些大停电事故主要是由连锁故障引起的，且与电网中的关键环节有着密切的联系［4］。由于连锁故障涉及的元件数目较多，故障形式复杂，因此，有必要辨识出电力系统中的关键元件，以便采取有针对性的措施。

文献［5］采用直流潮流法对电力系统进行连锁故障风险评估并找出了关键线路。文献［6］提出了基于边韧性度的电力系统关键线路筛选方法。文献［7］基于系统生存性评估理论，提出了一种新的关键线路识别方法。文献［8］基于模拟连锁故障的隐性故障模型，提出了系统的线路故障风险评估方法。文献［9］提出线路的电气介数，并将其用于电力系统关键线路识别。文献［10］基于网络最大流和复杂网络理论，提出了辨识电力网关键线路和节点的方法。以上方法和模型在一定程度上能有效地辨识关键元件，但还存在以下欠缺:

(1)保护装置的不正确动作往往是扩大故障范围的罪魁祸首，忽略了保护装置的故障因素是不恰当的;

(2)系统的初始状态模型和后续故障只考虑了线路的故障情况，过于简化，与实际情况不太相符。

基于上述考虑，本文首先根据Markov 状态空间理论建立了计及保护故障因素的系统初始状态概率模型，然后在后继故障阶段，建立了基于实时运行条件下的线路、发电机和负荷的可靠性模型，最后提出了模拟连锁故障的风险评估方法，辨识出关键线路和重要保护，仿真结果验证了其有效性和可行性。

1 初始状态概率模型

关联性是连锁故障最典型的特点［11］，即相互故障之间具有一定的联系，这也是分析连锁故障的难点。在连锁故障初期，系统往往表现为在较短时间内多个元件发生停运，且主要原因是保护装置的动作(包括正确动作和非正确动作)导致。本文为了计及保护之间及保护与元件之间的配合关系，将线路(含变压器支路)、主保护及相邻后备保护组成一个整体，然后基于Markov 状态空间将系统的初始状态划分为常见的4 类，并假设如下条件:

(1)不考虑保护系统检修状态和断路器故障。

(2)保护系统各保护单元的故障率λ 和维修率μ 为常数，其可靠度和维修度均服从指数分布。

(3)保护装置误动、拒动不同时发生。

基于上述假设的初始状态模型如图1 所示。

图1 初始状态空间图Fig.1 The initial state-space diagram

图1 中状态1 为线路、主保护和相邻后备保护都处于正常状态;状态2 为线路故障时，主保护正确动作，相邻后备保护误动;状态3 为线路故障时，主保护正确动作，相邻后备处于正常状态;状态4 为线路故障时，主保护拒动，相邻后备正确保护动作。各状态之间的转移关系如图1 所示。

根据Markov 状态方程，由图1 的状态空间图可得到其状态转移矩阵为

同时，假定其极限状态概率矢量为:P =［p1，p2，p3，p4］，由Markov 过程逼近原理可知:

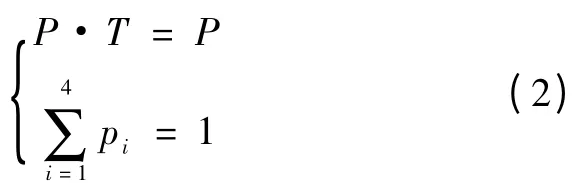
据式(1)和式(2)通过线性代数计算可以得到p1，p2，p3和p4的值，其中p2，p3和p4是初始故障状态的概率。

2 后继故障过程分析

2.1 概述

连锁故障过程一般可分为初始故障阶段和后继故障阶段。一般初始故障阶段的持续时间短，而后继故障阶段持续时间较长，整个连锁故障期间可能因为保护装置故障造成多个元件发生停运事件，从而导致发电机、负荷、母线从系统中脱离;另一方面，大范围的潮流转移还会引起更大范围的电压、频率、潮流越限，造成系统进一步的恶化，系统元件的可靠性降低。由此可看出，在后继故障阶段，系统的不良运行状况是造成连锁故障范围扩大的主要诱因之一。因此，本文在后继故障阶段建立了线路、发电机、负荷的可靠性模型。

2.2 基于线路潮流的线路可靠性模型

本文采用文献［12］的概率模型来描述电力系统中线路的停运概率，如图2 所示。

当线路潮流值小于潮流极限值时，线路停运概率很小且为常数PHL;当线路潮流值大于1.4 倍潮流极限值时，线路过负荷保护动作，线路停运概率为1;当线路潮流值处在潮流极限值与1.4 倍潮流极限值之间时，线路的停运概率与线路潮流成线性关系。如式(3):

图2 线路停运概率随潮流变化的曲线Fig.2 Curve of line outages probability varying with transfer capacity

式中:Flimit为线路潮流极限值。

2.3 基于电压、频率的发电机可靠性模型

当电压、频率过高或过低时，发电机低压保护、过电压保护、低频保护、高频保护就会动作。由于在实际应用中，不同厂家、不同型号的发电机的特性各不相同，因此，本文将采用简化的模型来统一描述发电机的可靠性，发电机的停运概率与电压、频率的关系分别如图3、图4 所示。

图3 发电机停运概率随电压变化的曲线Fig.3 Curve of generator outages probability varying with voltage

当发电机电压大于电压上限时，发电机过电压保护动作，发电机停运概率为1;当发电机电压小于电压下限时，发电机低压保护动作，发电机停运概率为1;当发电机电压处于正常范围内时，发电机的停运概率很小且为常数PHG。如式(4)所示:

式中:Umax为发电机电压上限值;Umin为发电机电压下限值。

图4 发电机停运概率随频率变化的曲线Fig.4 Curve of generator outages probability varying with frequency

同理，当发电机频率大于频率上限时，发电机高频保护动作，发电机停运概率为1;当发电机电压小于频率下限时，发电机低频保护动作，发电机停运概率为1;当发电机频率处于正常范围内时，发电机保护的停运概率很小且为常数PHG。如式(5):

式中:fmax为发电机频率上限值;fmin为发电机频率下限值。

2.4 基于电压、频率的负荷可靠性模型

当电压、频率降到保护装置的整定值以下，则负荷的低周、低压减载装置就会动作，切掉负荷(不考虑具体切负荷方案)。负荷的停运概率与电压、频率的关系分别如图5、图6 所示。

图5 负荷停运概率随电压变化的曲线Fig.5 Curve of load outages probability varying with voltage

类似地，负荷停运概率随电压变化的关系如式(6):

图6 负荷停运概率随频率变化的曲线Fig.6 Curve of load outages probability varying with frequency

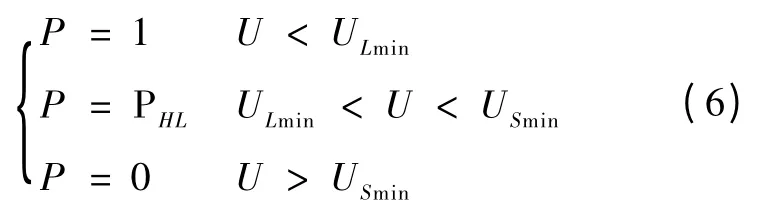
式中:ULmin为负荷电压下限值;USmin为母线电压下限值。

同理，负荷停运概率随频率变化的关系如式(7)所示:

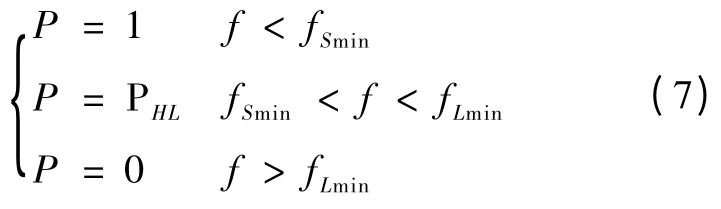
式中:fSmin为系统频率下限值，fLmin为负荷频率下限值。

3 评估指标

3.1 风险理论［8］

所谓风险，是指能导致伤害的或灾害的可能性和这种伤害的严重程度。因为风险具有可累加组合的性质，且风险指标能定量地表示风险等级的因素，所以使用风险指标既可以对个体也可以对整体进行定量评估。一般风险的表达式为

式中:R 为风险值;P 为事件的发生概率;I 为事件的产生后果。

3.2 连锁故障概率

连锁故障可看成若干个具有时序的系统状态集合，如图7 所示。

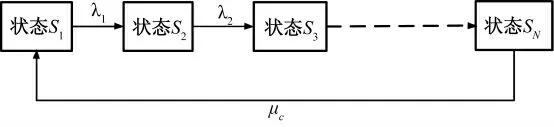
图7 连锁故障状态空间图Fig.7 State space diagram of cascading failure

图中λ1是激发元件的失效率;λ2是第二元件失效率;μc是连锁停运恢复率。第一个元件的失效引起第二个元件失效，第二个元件失效引起第三个元件失效，依此类推;相应的系统状态也从S1转移到S2，S2转移到S3，依此类推。因此，连锁故障的发生概率实质为条件概率，由条件概率公式可获得连锁故障序列的概率为

式中:P(S1)为系统初始状态的概率P0;P(S2|S1)，…，P(SN|S1，…，SN－1)分别为各个状态间的转移概率，记为P1，P2，…，PN－1，可由文献［13］的方法得到，则式(9)可表示为

3.3 风险计算

考虑到连锁故障的关联性，即后一次故障很大程度上依赖于前面一次故障，为了区分连锁故障中的每一级故障环节对系统造成的损失不同，本文定义权值为且认为如 式(11)所示。

式中:j =1，2，…，N 为连锁故障仿真序号;N 为仿真次数;i =1，2，…，Mj为第j 次连锁故障仿真中的故障环节序号;Mj是第j 次连锁故障仿真的故障总级数;参数β ＜1。

根据式(11)，当β趋近于1时，连锁故障中各级故障的权值比相等，而当β越小，权值比越大。在针对不同的系统时，可通过调整β以实现对权值的调整，且满足式(12):

本文定义第k 条线路(含变压器支路)的风险重要度为

式中:PL(k，j)为第j 次连锁故障，第k 条线路的停运概率;SL(k，j)为第j 次连锁故障，第k 条线路停运时，系统损失的功率;SB为系统基准功率;I 为N次连锁故障仿真中第k 条线路停运的集合。

本文定义保护k 的风险重要度为

式中:PT(k，j)为第j 次连锁故障，含保护k 故障的初始故障状态概率;ST(k，j)为第j 次连锁故障，保护k 发生故障时，系统损失的功率;SB为系统基准功率;J 为N 次连锁故障仿真中保护k 故障的集合。

4 算法流程

本文的算法流程如图8 所示，并对算法流程作以下几点说明:

图8 算法流程Fig.8 Algorithm flow

(1)考虑到过负荷保护的动作时间一般较长，所以本文在模拟支路开断时，交替执行稳定计算与潮流计算。

(2)本文不采取任何优化控制措施，评估结果可能偏于悲观，但本文的目的是找出系统的薄弱环节，即比较各线路及线路保护重要度相对大小，无需精确定量分析，所以结果是可以接受的，也是便于计算的。

(3)当潮流计算不收敛时，本文认为系统失去了稳定。

5 算例分析

本文采用WSCC －9 节点系统对所提出的算法进行仿真验证，如图9 所示。仿真计算过程中，初始状态 模 型 中 的 参 数 分 别 为［14，15］:λ1= 1.3，λ2=0.008 96，λ3=0.008 96，单位为次/年;μ1= 0.08，μ2=0.005，μ3=0.005，单位为次/h。后继故障中各模型参数分别为［12］:PHL=0.01，PHG=0.0167，Umax=1.3 p.u.，Umin=0.8 p.u.，fmax=52.5 Hz，fmin=46.5 Hz，PHF=0.016 7，ULmin=0.45 p.u.，USmin=0.85 p.u.，fSmin=46.5 Hz，fLmin=49 Hz。线路、变压器均等值为支路，按标幺值计算。

图9 算例系统Fig.9 Test system

经仿真计算得到:各条支路风险重要度指标如表1 所示，各个保护风险重要度指标如表2 所示，各条支路故障可能引发的连锁故障路径的数量和连锁故障路径的平均功率损失如图10 和图11 所示。

表1 支路风险重要度Tab.1 Branch line risk importance

表2 保护风险重要度Tab.2 Protection risk importance

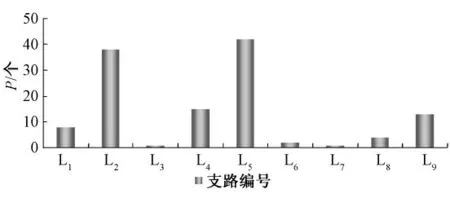
图10 连锁故障路径数量Fig.10 The number of cascading failures path

图11 连锁故障路径的平均功率损失Fig.11 The average power loss of cascading failures path

从表1 可看出支路L7，L6是风险重要度最大的2 条支路，根据风险具有可累加组合的性质，原因主要有两种:一种可能是支路L7，L6作为多个连锁故障中的某一级故障环节，虽然每次造成的风险并不突出，但累加后总的风险较高;另一种是支路L7，L6作为故障环节的次数不多，但每次造成的风险较高，总的风险也较高。当然，也可以是两者的任意组合。因此，支路L7为关键支路，线路L6为关键线路。但同时从图9 和图10 可发现，如果线路L2，L5作为起始故障线路时，会给系统带来很大的连锁故障风险，这主要是因为线路L2，L5作为发电机2 的出口线路，承担着功率外送的重要任务，所以对线路L2，L5应进行重点监控，以防止连锁故障发生。

从表2 可看出7 号、15 号和11 号保护的风险重要度最大，从图11 可知这3 个保护分别在连锁故障路径平均功率损失最多的起始支路L5，L2，L4上，这是因为保护的误拒动主要集中在连锁故障初始阶段，所以7 号、15 号和11 号保护在连锁故障初始阶段的不正确动作会给系统带来严重的后果，对故障范围的扩大起着推波助澜的作用。因此，7 号、15 号和11 号保护为本系统的重要保护，需要重点加强和保护。综上，算例的结果验证了该方法的正确性和可行性。

6 结 论

本文基于连锁故障模型和风险理论，提出了辨识系统中关键线路和重要保护的方法。该方法在初始状态概率模型中考虑了多种初始状态的组合，计及了保护故障因素，在连锁故障的后继故障阶段，考虑了基于实时运行条件的线路、发电机、负荷可靠性模型，从而提出了基于连锁故障模型的风险评估方法。基于本文提出的方法，找出了WSCC －9 节点系统的关键线路和重要保护，有效地识别出系统中的薄弱环节。本结论对提高电力系统的稳定性和可靠性有着十分重要的意义。

［1］McCalley J D，Zhu K，Chen Q M.Dynamic decision-event trees for rapid response to unfolding events in bulk transmission systems［C］.Power Engineering Society Summer Meeting，Vancouver，Canada，2001，2:15 －19.

［2］石立宝，史中英，姚良忠，等.现代电力系统连锁性大停电事故机理研究综述［J］.电网技术，2010，34(3):48 －54.

［3］高翔，庄侃沁，孙勇.西欧“11.4”大停电事故的启示［J］.电网技术，2007，31(1):25 －31.

［4］张保会.广域动态条件下电网安全紧急控制的研究［J］.电力自动化设备，2005，25(8):1 －8.

［5］杨明玉，田浩，姚万业.基于继电保护隐性故障的电力系统连锁故障分析［J］.电力系统保护与控制，2010，38(9):1 －5.

［6］刘影，王涛，顾雪平.基于边韧性度的电力系统关键线路筛选［J］.电力系统保护与控制，2012，40(6):92－103.

［7］杨文辉，毕天姝，黄少锋，等.基于电网生存性评估的关键线路识别方法［J］.中国电机工程学报，2011，31(7):29 －35.

［8］丁理杰，刘美君，曹一家，等.基于隐性故障模型和风险理论的关键线路辨识［J］.电力系统自动化，2007，31(6):1 －5.

［9］徐林，王秀丽，王锡凡.电气介数及其在电力系统关键线路识别中的应用［J］.中国电机工程学报，2010，30(1):33 －39.

［10］鞠文云，李银红.基于最大流传输贡献度的电力网关键线路和节点辨识［J］.电力系统自动化，2012，36(9):6 －12.

［11］王英英，罗毅，涂光瑜，等.电力系统连锁故障的关联模型［J］.电工技术学报，2012，27(2):204 －209.

［12］Chen J，Thorp JS，Dobson I.Cascading dynamics and mitigation assessment in power system disturbances via a hidden failure model［J］.Electrical Power and Energy Systems，2005，27(4):318 －326.

［13］Cheng L，Liu H T，Zou X，et al.Short-term reliability online evaluation basing on transient state probability［C］//Proceedings of Power Engineering Society General Meeting.FL，USA:Tmpa.2007:24 －28.

［14］X Yu XB，Chanan S.A practical approach for integrated power system vulnerability analysis with protection failures［J］.IEEE Transaction on Power Systems，2004，19(4):1811 －1820.

［15］熊小伏，欧阳前方，周家启，等.继电保护系统正确切除故障的概率模型［J］.电力系统自动化，2007，31(7):12 －15.