超临界机组协调控制方法研究及模型分析

谷俊杰，冀乃良，曹晓威，杨 扬

(1.华北电力大学 能源动力与机械工程学院，河北 保定071003;2.华能上安电厂，河北 石家庄050310;3.保定热电厂，河北 保定071051)

0 引 言

目前，600 MW 超临界机组已成为国内新建和扩建机组的主要发展趋势，其主汽压力和主汽温度提升，可大大提高机组热效率和经济性，是我国电力行业的主力机组。由于超临界机组容量大、控制参数多、系统复杂的特点，对机组自动化水平提出更高的要求。

机组协调系统是有锅炉和汽轮发电机组两部分组成，是一个具有强耦合性的多输入多输出系统，负荷和主蒸汽压力控制相互制约，机组动态本质上是非线性的，汽轮机侧相应较快，锅炉侧存在很大的迟延。虽然可以利用锅炉蓄热暂时有效控制输出量，但随着电网和机组容量的不断扩大，蓄热可利用率减小［1］，参与电网综合自动化、实现自动发电控制的要求也越来越高，而机组协调控制系统作为联结发电机组与电网的纽带，其控制品质的改善是提高电厂运行水平的关键。因此研究此系统的控制问题具有重要意义。

1 格拉姆矩阵解耦简化分析

基于子系统能控能观性的格拉姆法［2］是对机组模型解耦简化的简单有效方法之一。一个系统是否可控，仅与状态方程有关，而与系统输出方程无关，因此定义系统的可观可控性只需利用状态方程来进行［3］。

设连续线性定常系统状态空间描述为

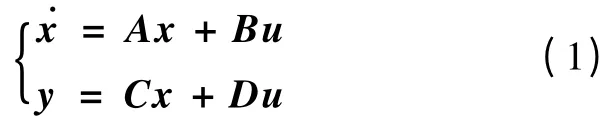
式中:x 为n 维状态向量;u 为p 维输入向量;A 为n × n 维矩阵;B 为n × p 维状态矩阵。若在［t0，∞］ 区间内u 为分段连续函数向量，则称其为容许控制。

格拉姆法将整个系统分为多个子系统，利用各子系统中包含能控能观性的矩阵比较来得出更有利于控制系统设计的配对方式。格拉姆法在消除部分通道间耦合、避免控制结构过于复杂的同时，也提高了控制系统的性能。但是随着系统维数的增多，控制系统结构也会变多，因此需要通过格拉姆法矩阵解耦法选择合适的控制结构。

系统完全可控的充要条件是，存在时刻t1＞0，使如下定义的格拉姆矩阵为非奇异［4］。

则称式 (2)为格拉姆矩阵可控性判据。可以看出在应用格拉姆矩阵判据时，需要计算矩阵指数e－At，但在A 的维数n 比较大时，计算e－At是比较困难的，所以格拉姆矩阵判据一般用于做理论分析。

系统 (1)完全可观测的充要条件是，存在时刻t1＞0，使如下定义的格拉姆矩阵为非奇异。

则称式 (3)为格拉姆矩阵可观测性判据。假定式 (1)所示的系统稳定，设可控格拉姆矩阵为P ∈Rn×n，可观格拉姆矩阵为Q ∈Rn×n，且正定时常矩阵P、Q 满足李亚普诺夫方程式:

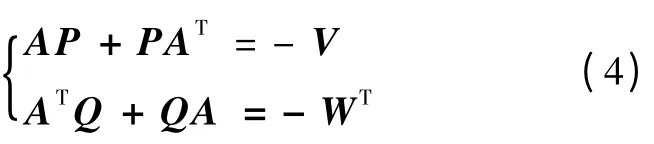
对于初等系统，每个子系统都有单输入μi(i∈{1，2…，m})和单输出yj(j ∈{1，2…，m})，并且每个状态控件模型(A，vi，cTj ，0)的格拉姆矩阵Pi和Qj均满足李亚普诺夫方程式:

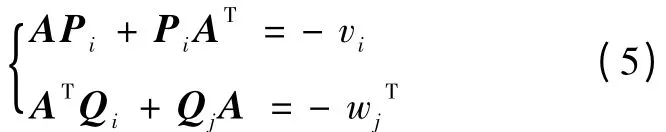
式中:vi是矩阵V 的第i 列，wj是矩阵WT的第j列。

设矩阵V，WT满足

故可以证明原系统的可控及可观格拉姆矩阵P 和Q 可以分解为

故可以得到:

那么，P、Q 的乘积可以可以看作是m2个单输入单输出系统Pi、Qj乘积。为了有实践性，以上的分析需要有一种量化，定义参与矩阵Φ =其中

注意到，经过对系统能观能控性分析之后，复杂的控制器结构可以被接近1 的φij之和代替［5］。基于Gramian 法的变量配对要求，选择使对应的φij值总和尽量接近于1，φij值和越接近于1，证明解耦效果越好［6］。

2 超临界机组结构分析及模型研究

通过热解实验，锅炉是一个分布参数对象，但出于简化考虑，目前在锅炉的建模与仿真中一般都采用集总参数模型来近似描述这类分布参数对象。本模型以各段的出口参数为各段的集总参数，根据质量守恒定律、能量守恒定律可以建立对象的数学模型，模型的连接如图1［7］。在总体模型的构建过程中，本文采用了分段推理，集中求解的方法，对过热区模型、汽水分离器模型、蒸发区模型、汽轮机测模型、炉膛燃烧模型公式，进行拉普拉斯变换后，再按图1 的连接方式联系起来，就构成了一个以汽轮机调门开度ΔμT、燃料变化量Δm 、给水阀开度变化量Δμd为输入，并以机前压力变化量ΔPt、机组输出功率ΔN 和中间点焓值变化量ΔH 为输出的模型，其结构如下:

通过对部分分散控制结构的分析，对式(10)中传递函数矩阵:

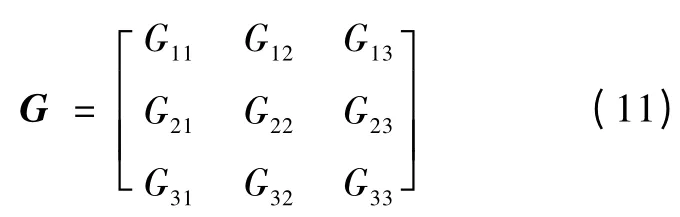
利用Gramian 方法进行能控能观性分析，可以得到其判别阵:

其 中:φ11、φ12、φ13、φ21、φ22、φ23、φ31、φ32、φ33分别表示ΔμT、Δm、Δμd分别对ΔPT、ΔN、ΔH 各子系统的能控能观性控制。由判别阵 (12)可知:∑≥0.99，因此，选择φ11、φ12、φ21、φ22、φ33的控制结构，从物理意义上来说，这是合理的。此时可以将直流机组三输入三输出的系统式 (10)转换成近似线性化模型系统式 (14)，该模型的具体形式如下:

3 超临界机组协调控制系统的工程应用及控制效果仿真

通过上述对系统的能观能控性分析可以确定，当煤水参数配比合适时，机组的协调控制类似于汽包炉［8］，因此可以建立类似于汽包炉的机组简化数学模型。本文在进行模型特性试验时是在煤水配比准确的基础上进行的，即在煤水基准线准确且动态过程中，煤到水的惯性时间合适，利用煤水比对中间点温度进行控制，此时可以将直流机组的三输入三输出系统转换成两输入两输出系统的近似线性化模型，该模型的具体形式如下:

其中，传递函数如下所示:

通过仿真可知，G22与G12曲线类似，故当参数k1、k2调整合适的情况下，二输入二输出的协调控制系统模型可以简化为如图2 所示。在仿真过程中，应用MATLAB 中的Simulink 建立系统模型，控制器可应用其中的工具箱进行编辑，并对算法实现适当的参数设置，仿真结果如图3、图4 所示。其中图3 为负荷跟随响应曲线，仿真时间为200 s 时将负荷由额定值增加20%，主蒸汽压力保持额定值不变;图4 为压力跟随响应曲线，仿真时间为200 s 时将主蒸汽压力由额定值增加20%，负荷保持额定值不变。

从仿真曲线可以看出，经过解耦简化以后的协调控制系统在满足控制高性能要求的同时，也使系统结构得到了简化。由此可见，格拉姆矩阵法在简化完全多变量控制结构的复杂性时，也能保证控制系统的高性能要求，甚至在某些响应的性能指标上优于多变量控制器。

图2 机组简化模型连接示意图Fig.2 Skatch map of unit simplify model linking

图3 负荷跟随试验Fig.3 Load following responses

图4 压力跟随试验Fig.4 Pressure following responses

4 结 论

本文针对600 MW 超临界机组控制系统强耦合多变量的特点，应用格拉姆矩阵解耦方法，对系统进行解耦简化。同时，利用响应曲线的相似性，将理论上的协调控制系统，简化为当前工程中普遍应用的控制系统，并通过仿真模拟，验证了该解耦策略的可行性，便于工程实践，具有较好的应用价值。

由于超临界机组参数的多样性，本文所提出的解耦策略不一定具有普适性，具体的结构还应该结合机组模型进行具体分析。若系统为高阶对象，控制系统的性能有待进一步研究。

［1］刘吉臻，协调控制与给水全程控制［M］.北京:中国电力出版社，1995.

［2］Conley A，Salgado M E.Grammian based interaction measure ［C］.Proceedings of IEEE Conference on Decision and Control，Sydney，Australia，2000.

［3］王春民，刘兴明.连续与离散控制系统［M］.北京:科学出版社，2008.

［4］胡寿松.自动控制原理［M］.北京:科学出版社，2001.

［5］ 赵冬梅.多变量系统鲁棒部分分散控制器设计［D］.北京:华北电力大学，2009.

［6］楼冠男，谭文.部分分散控制及其在单元机组协调控制中的应用［J］.中国电机工程学报，2011，31(2):91 -95.

［7］王恭良，沈炯，李益国.适用于控制的600 MW 超临界机组的简化模型［J］.江苏电机工程，2008，(4):1 -7.

［8］李泉，陈波，张华磊.超临界直流机组模型及控制优化［J］.中国电力，2010，(12):60 -63.