设置垫板的T形件螺栓连接力学性能有限元分析

吴兆旗，朱晓明，郑剑智，喻露

(福州大学土木工程学院，福建福州 350116)

0 引言

传统T形件连接通过螺栓将两个T形件翼缘直接相连而成，常用来模拟钢结构梁－柱螺栓连接节点受拉区的性能［1－2］.地震作用下梁柱节点主要承受往复弯矩作用，静力荷载作用下的受拉区则被往复拉压.Swanson等人［3］和Piluso等人［4］研究了T形件连接在往复拉压荷载作用下的滞回性能，并建立了相应设计方法和荷载－变形关系滞回模型.为增强连接耗能，Latour等人［5］将T形件翼缘设计成漏斗形状，通过试验研究分析其耗能能力和低周疲劳问题.

课题组提出在传统T形件翼缘之间设置垫板，使翼缘在压力作用下也能形成塑性铰，从而达到提高其耗能能力的目的［6－7］;并将设置垫板的T形件作为耗能元件应用于梁－柱节点，对其性能进行了数值模拟和试验研究，初步验证了连接构造措施的可行性［8－9］.为深入研究该类连接的性能，文献［10］完成了其在往复拉压作用下的拟静力试验研究工作.本研究在试验工作的基础上，采用ABAQUS软件对设置垫板的T形件连接在单调和往复拉压作用下的的力学性能进行模拟，分析讨论了不同参数对连接承载力、刚度、耗能能力等性能的影响.

1 有限元模型的建立

1.1 试件情况

共设计了5个试件，其中4个设置垫板，另外1个为传统不设置垫板试件以供对比.试件变化的主要参数为T形件长度b和垫板宽度lp，具体情况见表1.试验只考虑延性连接情况，即超载后T形件翼缘屈服，但螺栓不出现脆性断裂.T形件截面尺寸为63.5 mm×150 mm×6.5 mm×6 mm，翼缘和腹板连接处圆角半径为15 mm，采用Q235钢材制作;垫板厚度取为20 mm，采用Q345钢材制作;采用10.9级M16摩擦型高强度螺栓，中心线到T形件翼缘边缘的距离为25 mm.

表1 试件几何尺寸Tab.1 Dimensions of specimens (mm)

1.2 单元选择及网格划分

T形件、垫板和辅助装置采用八节点六面体单元C3D8R来模拟，各组件之间的接触和分离采用相应的界面单元来模拟.根据文献［11］建议的方法建立螺栓模型，即螺栓杆螺纹部分用具有螺栓有效直径的圆柱体代替，其余无螺纹部分则采用螺栓名义直径，垫圈和螺栓杆不直接相连;沿受弯板件厚度方向划分三个单元以获取较高的计算精度［12］，划分网格后的有限元模型如图1所示.试件受拉时，采用如图1(a)的对称结构形式;试件受压或者往复拉压时，为防止结构发生非预期失稳，T形件利用两个螺栓固定在代表柱翼缘的辅助装置上，如图1(b)该辅助装置顶板厚40 mm，并设有加劲肋.

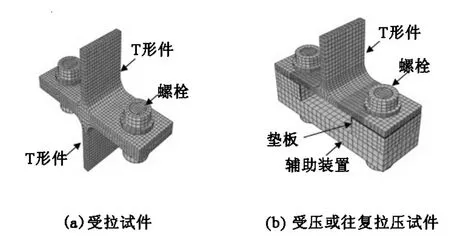
图1 试件有限元模型Fig.1 Finite element model of specimens

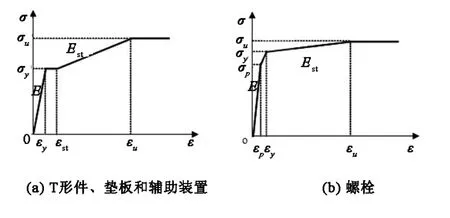
图2 材料应力－应变关系图Fig.2 Stress－ strain relationship of steel and bolt

1.3 材料的本构关系

根据钢结构材料的弹塑性特点，T形件、垫板和辅助装置材料的应力－应变关系近似简化为如图2(a)所示的折线.E为钢材弹性模量;Est为钢材强化阶段的模量;εy为屈服应变;σy和σu分别为钢材的屈服强度和极限强度.取屈服极限应变εst=10 εy;强化极限应变εu=100 εy.对于螺栓材料包括螺栓体、螺栓头、螺栓帽，其应力－应变曲线如图2(b)所示.σp为钢材的弹性比例极限;εp为弹性极限应变;εy为对应残余应变为0.002时的应变值.强化极限应变εu=8 εy.材料均为各向同性，弹性模量取2.06×105MPa，泊松比取为0.3.计算中采用Von－Mises屈服准则及其关联流动法则，材料强化模型采用多线性随动强化准则.

1.4 边界条件及加载

模型中考虑了T形件翼缘之间、垫板与T形件翼缘及钢板之间、螺栓头垫圈与T形件翼缘及钢板之间、螺栓杆与栓孔之间的接触，所有接触均采用面－面接触，选用有限滑移算法.接触面切线方向采用库伦摩擦，摩擦系数取为0.4，由于考虑的是摩擦型高强螺栓的连接形式，螺栓杆与孔壁之间的摩擦系数为0，法向方向为硬接触.

底部端面每个节点限制三个方向的位移.荷载施加及计算过程为:①对螺栓施加很小的预拉力，让各个接触关系平稳地建立起来，利用Bolt Load对螺栓施加预拉力;②将螺栓预拉力增加到相应设计值，预拉力设计值按照《钢结构设计规范》GB50017［13］的规定取为100 kN;③将螺栓预紧力改为固定螺栓的长度，并对上部T形件腹板顶端施加垂直于翼缘平面的位移荷载.

2 计算结果及分析

2.1 受拉性能分析

试件TC－N－50、TC－P－50－38和TC－P－50－42三个试件在受拉荷载作用下的荷载－位移关系曲线如图3所示，其中试验测得结果来源于文献［10］.从图3可以看出，有限元结果与试验结果吻合良好，说明元分析模型能够很好的分析设置垫板和不设置垫板的T形件连接受拉性能.

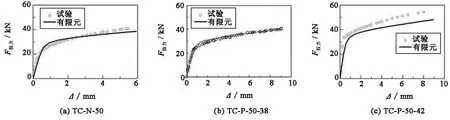
图3 数值分析与试验结果对比曲线Fig.3 Contrast curves of numerical analysis and test results

有限元分析得到的所有试件在受拉作用下的荷载－位移关系曲线如图4所示.从图4可以看出:设置垫板对连接受拉性能影响不大.主要原因是设置垫板并没有改变T形件翼缘的约束条件，也没有改变螺栓与T形件腹板之间的相对位置;增大T形件长度L对连接的刚度和承载力均有提高.L由50 mm增大到60 mm时，受拉承载力提高13.6%.

以试件TC－P－50－38为例，详细分析连接在拉力作用下的性能.螺栓施加预拉力后，试件各部分处于弹性状态;当位移荷载为0.57 mm(对应外力为25.4 kN)翼缘与腹板连接倒角处和螺栓头外侧的翼缘开始屈服，如图5(a)所示;随着荷载的增加，塑性区域继续扩展.位移荷载加至4.5 mm(外力为36.8 kN)，T形件翼缘出现明显屈服变形，如图5(b)所示;当位移荷载为7.5 mm(外力为40.4 kN)，T形件翼缘变形显著，塑性铰基本形成，靠近腹板的螺栓由于约束作用加强也出现屈服，如图5(c)所示;图5(d)表示位移荷载为10 mm时，塑性区域扩展至全截面，塑性铰完全形成.最终失效发生于T形件翼缘在靠近腹板和螺栓中心线处形成塑性铰.由于垫板的钢材等级较高，加载过程始终处于弹性阶段.

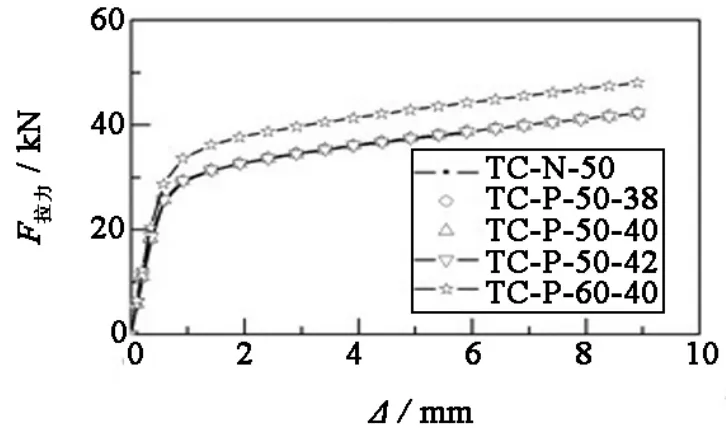
图4 试件拉力荷载－位移曲线Fig.4 Tension load － deformation relationship curves

图5 试件TC－P－50－38塑性应变图Fig.5 Plastic strain development process of TC－P－50－38

2.2 受压性能分析

T形件翼缘之间设置垫板，为受压时反向变形提供了空间，使其在压力作用下也能屈服.图6给出试件TC－P－50－38、TC－P－50－40、TC－P－60－40在压力作用下有限元分析和试验［14］测得的荷载－位移关系曲线.从图6中也可以看出，有限元分析结果与试验结果拟合较为一致.

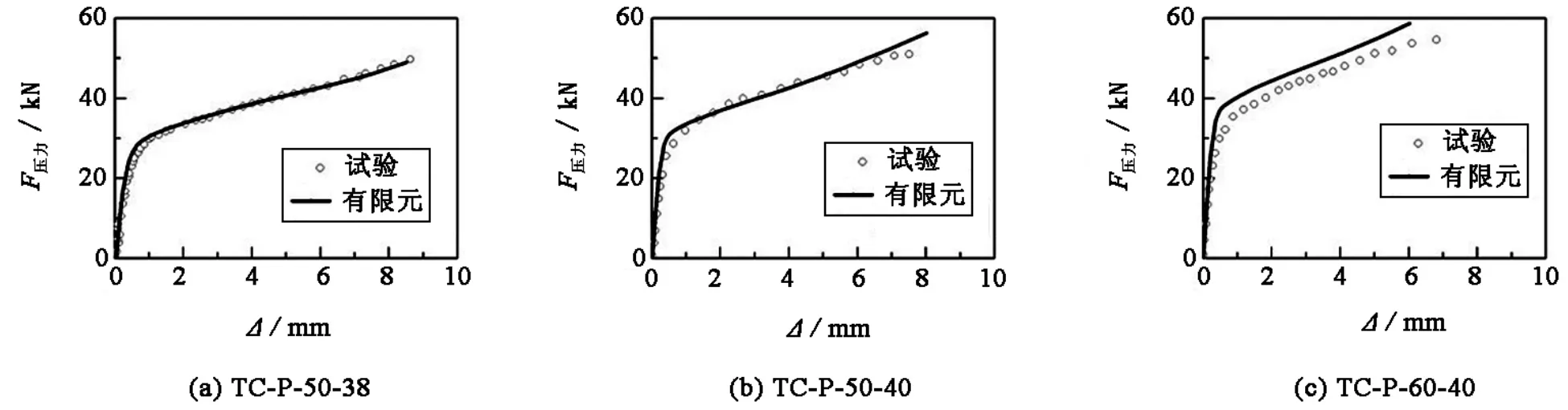
图6 数值分析与试验结果对比曲线Fig.6 Contrast curves of numerical analysis and test results

所有设置垫板试件的荷载－位移关系曲线如图7所示.从图7可以看出:①随着垫板宽度的增加，连接刚度和承载能力均有所增加.TC－P－50－40试件的承载力和初始刚度较TC－P－50－38试件分别增大了18.4%和39.4%;TC－P－50－42试件的承载力和初始刚度较TC－P－50－38试件分别增大了31.2%和64.2%;TC－P－50－42试件的承载力和初始刚度较TC－P－50－40试件分别增大了10.8%和17.8%.② 随着T形件长度b的增加，连接的初始刚度和承载能力均有所增加.TC－P－60－40试件的承载力和初始刚度较TC－P－50－40试件增大了18.7%和20.7%.

压力荷载作用下TC－P－50－38试件塑性应变图如图8所示.螺栓施加预拉力后，各部件处于弹性状态.当施加的位移荷载为0.2 mm时，垫板边缘处的T形件翼缘开始屈服(图8(a))，此时产生的外力为16.6 kN;当位移荷载增加至4.5mm(外力为24.8 kN)时，T形件腹板与翼缘连接的倒角处也发生屈服，垫板处的塑性区域进一步发展，塑性铰开始形成，如图8(b)所示;位移加载至7.5 mm(外力为46.1 kN)，螺栓垫片底部也开始屈服，T形件翼缘出现明显变形(图8(c));位移为10 mm(外力为53.9 kN)时，T形件翼缘塑性变形明显，塑性铰已基本形成(图8(d)).最终的失效模式为T形件翼缘与腹板连接的倒角处和垫板边缘处形成塑性铰.在受压作用下高强螺栓具有足够的刚度对翼缘进行约束，整个加载过程没有发现翼缘翘起现象.

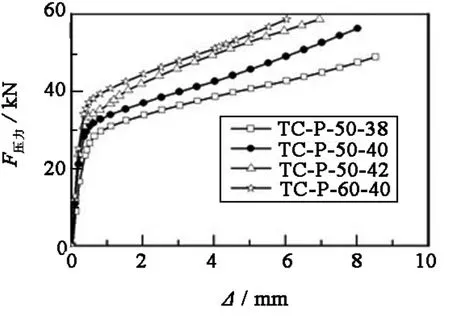
图7 试件压力荷载－位移曲线Fig.7 Compression load － deformation relationship curves

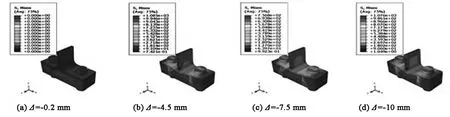
图8 试件TC－P－50－38塑性应变图Fig.8 Plastic strain development process of TC－P－50－38

2.3 滞回性能分析

往复拉压荷载作用下各试件荷载－位移关系滞回曲线如图9所示.从图9可以看出，各试件的滞回曲线饱满、稳定，在多次循环中强度和刚度没有明显降低;有限元计算结果和已有试验结果相比，吻合良好;未设置垫板试件TC－N－50只能在受拉时耗散能量，而设置垫板试件在拉压两个方向均能耗散能量;设置垫板试件耗散能量约为同尺寸传统试件的1.5～2倍;随着设置垫板宽度的增加，试件耗能能力略有提高;随着T形件长度b增加，连接的耗能能力增加，但极限变形变化不大.

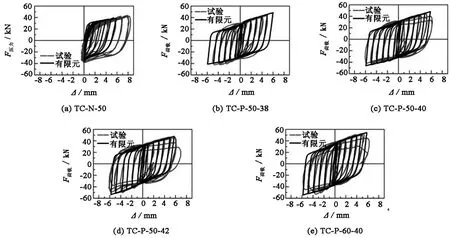
图 9试件荷载－位移滞回曲线Fig.9 Hysteretic loops of load － deformation of specimens

3 结论

1)建立的有限元模型能够很好的模拟设置垫板T形件连接在单调拉力、单调压力和往复拉压作用下的性能，能够用来在更大范围内调查该类型连接的性能;

2)设置垫板T形件连接在往复拉压作用下滞回性能稳定、滞回环饱满，在拉压方向上均能耗散能量，其耗能能力为不设置垫板的T形件连接的1.5～2倍左右;

3)设置垫板对连接抗拉刚度和承载力等性能影响不大;随着设置垫板宽度增加，连接的抗压刚度和承载力均有一定程度的增加;

4)随着T形件长度的增加，连接拉压刚度、承载力和耗能能力均有提高.

［1］European Committee for Standardization.DIN EN 1993－1－8－2010 Eurocode 3:Design of steel structures Part 1－8:Design of joints［S］.Brussels:European Committee for Standardization，2005.

［2］Faella C，Piluso V，Rizzano G.Structural steel semirigid connections:theory，design and software［M］.London:CRC Press，2000.

［3］Swanson J，Leon R.Bolted steel connections:tests on T－stub components［J］.Journal of Structural Engineering，2000，126(1):50–56.

［4］Piluso V，Rizzano G.Experimental analysis and modelling of bolted T－stubs under cyclic loads［J］.Journal of Constructional Steel Research，2008，64:655－669.

［5］Latour M，Rizzano G.Experimental behavior and mechanical modeling of dissipative T－stub connections［J］.Journal of Structural Engineering，2012，138(2):170 －181.

［6］吴兆旗，姜绍飞，曾建仙，等.易修复钢结构梁柱节点:中国，ZL2010 1 0164386.1［P］.2011－06－22.

［7］吴兆旗，何田田，姜绍飞，等.钢结构梁柱连接节点抗震性能研究进展［J］.福州大学学报:自然科学版，2011，39(5):658－665.

［8］Wu Zhao－qi，Su Jian－qiang，Jiang Shao－fei.Determination of design bending moment of a T－stub connection with inserted plates［J］.Advanced Science Letters，2012，9(1):642 －646.

［9］吴兆旗，苏建强，姜绍飞，等.设置垫板的梁－柱T形件连接节点滞回性能试验研究［J］.建筑结构学报，2012，33(12):10－19.

［10］邱骏达，吴兆旗，刘志航，等.设置垫板的T形件连接滞回性能试验与数值模拟［R］.福州:福州大学，2012.

［11］Wu Zhao－qi，Zhang Su－mei，Jiang Shao－fei.Simulation of tensile bolts in finite element modeling of semi－rigid beam －to－column connections［J］.International Journal of Steel Structures，2012，12(3):339 －350.

［12］Bursi O S，Jaspart J P.Basic issues in the finite element simulation of extended end plate connections［J］.Computer and Structures，1998，69(3):361－382.

［13］中华人民共和国建设部.GB 50017－2003钢结构设计规范［S］.北京:中国计划出版社，2003.