地震一致激励计算方法的比较与分析

杨斌斌，龙晓鸿，樊剑，李俊，陈蓓蕾

(华中科技大学土木工程与力学学院，控制结构湖北省重点实验室，湖北武汉 430074)

0 引言

地震动激励包括一致激励和多点激励，对于一些平面尺寸较小的结构体系而言，通常一致激励分析可以满足工程需要;然而在现代土木工程建造中，由于结构的大跨性等特征，以及地震地面运动的空间变异性特点，使得结构物各支座往往承受多点地震激励.因此，通过地震一致激励各种计算方法的比较与分析，寻找更加有效可靠的分析方法用于地震多点激励分析显得尤为重要.

地震作用下结构的响应分析计算，传统上采用加速度直接输入，并得到了广泛的应用.但柳国环［1］等对结构地震响应计算模型进行对比分析，认为一致激励时采用位移输入模型更加合理.针对直接位移输入，Edward L Wilson［2］研究了位移荷载下的地震分析，指出位移荷载直接输入下，会激发更多的高阶模态，需要更小的积分步长或者更精确的积分方法.柯世堂［3］等对位移荷载输入的动力时程法进行研究，分析了误差的来源.除此之外，众多学者通过进一步的研究分析认为大质量法(large mass method，LMM)和大刚度法(large stiffness method，LSM)是较好的近似计算方法.周国良［4］等对LMM在应用中产生的误差进行了分析研究并提出了改进方法.王波［5］等利用LMM对高墩大跨连续刚构桥进行分析，综合比较了地震一致激励与考虑行波效应激励下高墩的地震反应.周国良等［6］借助简单模型对LSM 在结构动力分析中的应用以及误差分析与改进方法进行了系统研究.但是这些研究均未对各种方法进行系统的比较分析，也未得出它们的适用范围.本研究在介绍两种输入模型的基础上，系统的分析几种计算方法的处理方法、误差来源以及改进方法，并指出各自的优缺点以及适用性.在此基础上，以北盘江大桥为例，验证加速度输入、LMM和LSM在一致激励分析中的一致性和可靠性.

1 地震激励的分析模型及计算方法

1.1 地震激励分析模型

地震地面运动下，结构动力反应的数值分析模型主要有两种:一致加速度输入和直接位移输入模型.

对一离散单元的结构体系，与地面刚性连接，地震地面运动下，该体系的动力平衡方程可表达为:

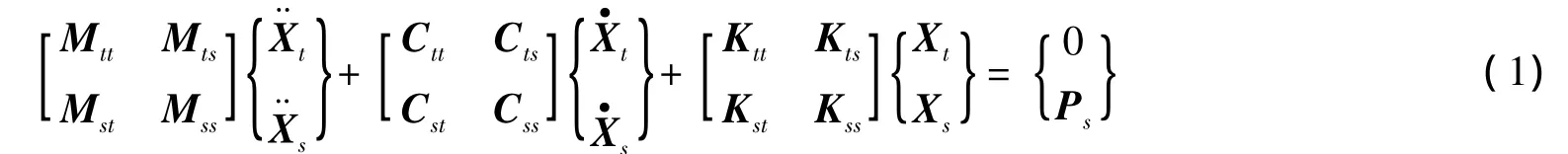
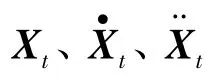
通常忽略阻尼项Ctss，此时式(2)即为求解结构地震响应的位移输入模型.

将式(2)按照拟静反应和动反应两部分分解，可得式(3)，具体推导参考文献［1］.

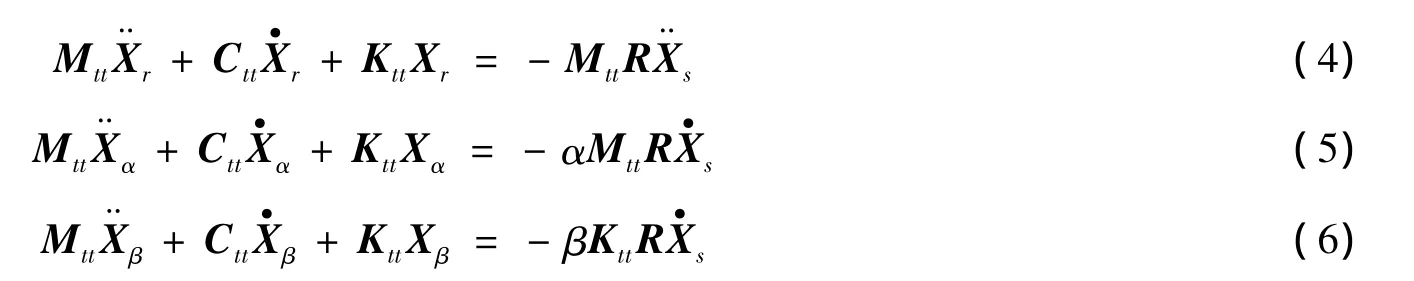
式(4)－式(6)即为式(2)在忽略阻尼项后的等价变形，式(4)即为常采用的一致加速度输入模型.

1.2 四种计算方法的比较分析

1.2.1 加速度输入法

加速度输入计算是建立在相对坐标下的动力平衡方程，计算得到的反应是相对量，并且在一致激励分析中得到认可与应用，但大跨结构通常承受多点激励，而加速度输入不适用于多点激励计算，因此计算大跨结构多点激励需要更加合理的输入方式.

1.2.2 直接位移输入法

直接位移输入法可直接求得地震动激励下结构的绝对位移响应，但在直接位移输入时，一方面，通常忽略阻尼项Ctss，但对大跨隔震结构而言，大跨结构支座处通常有阻尼器所提供的集中阻尼即Cds，Cd为阻尼器的阻尼系数矩阵.因此，对于此种情况，忽略阻尼器阻尼会带来较大的影响;另一方面，直接位移输入模型与一致加速度输入模型相比，多出了两项－αMttEg和βKtsE

g的影响，通常－αMttE

g可以忽略［1］;而βKtsEg以集中力或力偶的形式作用于结构底部质点上，因此会导致结构底部节点处剪力和弯矩等出现不合理的增大.

除此之外，地面运动位移是由加速度积分而来，通常假设加速度在每一时间步长内按线性变化，而位移则在每一时间步长内是时间的三次函数［3］.同时，直接位移输入时还会激发大量的高阶频率，由加速度积分得到位移时，当中的运动学关系还没有一个令人信服的结论.

针对上述问题，李宏男［7］对直接位移输入模型采用基底加无质量元进行改进，并以简单模型加以验证，但其实际工程应用仍受到一定的限制.

1.2.3 LMM

LMM是将结构基础假设为一个或多个附着于结构基础或支撑点的具有大质量的几种质量单元M0(一般上取结构总质量的106倍以上)，结构动力分析时释放基础运动方向的约束，并在大质量点处施加动力Ps模拟基础运动，其中Ps=M0，将Mss+M0代替Mss代入式(1)，并将式(1)中的下式展开得:

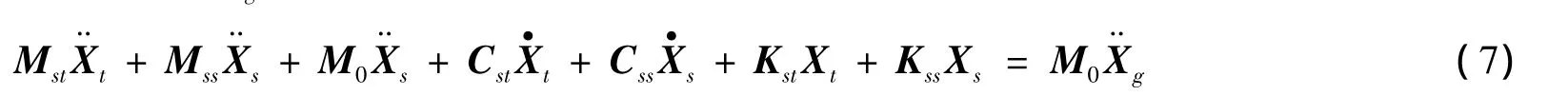
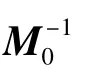
同时，将式(1)的上式展开并考虑式(9)整理得:

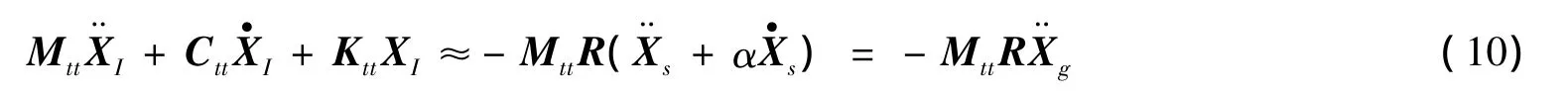
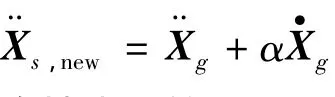
LMM是多点激励响应分析的常用方法，虽是一种近似算法［8］，但可以用于考虑地面运动的空间变异性对结构动力的影响，尤其适用于长周期的结构计算.

1.2.4 LSM

LSM是在结构基础地震激励方向去掉约束，设置一个大刚度弹簧单元(其刚度取地震激励方向上各单元刚度之和的106倍)，在大刚度弹簧上施加动力时程Ps模拟基础运动，其中Ps=KssXg，将其代入式(1)，并将(1)式中的下式展开得:

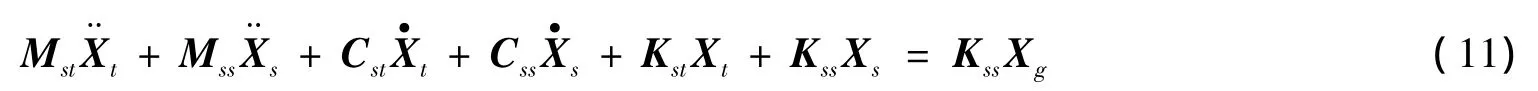
由于β并非无穷小量，所以忽略时将会产生误差，同时，将式(1)的上式展开整理得:

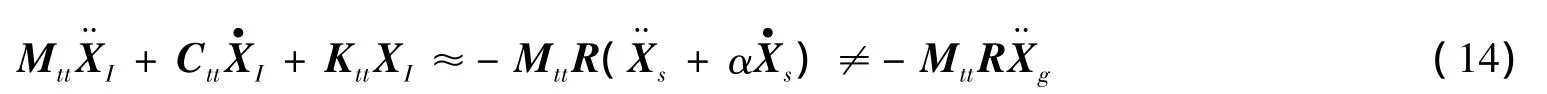
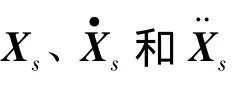
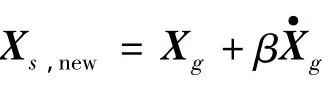
运用LSM进行地震激励分析时，刚度阻尼系数β=ξTiπ(1+γ)，γ=ωjωi，Ti越小，β影响较小，因此，LSM只能粗略的用于β足够小的情况，否则应对输入的地震动位移进行修正.

2 算例分析

2.1 工程背景

北盘江大桥跨越北盘江峡谷，桥梁全长1 261 m，主桥中心桩号为k31+345，桥跨布置为:(5×30 m)+(82.5 m+220 m+290 m+220 m+82.5 m)+(3×30 m)+(4×30 m)，其中主桥为预应力混凝土空腹(斜腿)式连续刚构，跨度82.5 m+220m+290m+220m+82.5m，引桥采用预应力混凝土T梁先简支后结构连续的形式;引桥桥墩采用单排双柱式，桥墩采用桩基础，桥台采用桩柱式台;主墩6#、7#、8#和9#采用空心薄壁墩，横、顺桥方向均为双肢悬浇T型墩，高度分别为75、90、143和68 m，其中7#、8#墩在斜腿交汇点以上采用等截面，以下部分以及6#、9#墩都按1∶100放坡，最高8#主墩在底部51 m处两肢桥墩间采用0.5 m厚薄壁连为整体，其桥型布置结构形式如图1.

图1 北盘江大桥桥型Fig.1 The type of Beipanjiang bridge

采用大型通用有限元分析程序ANSYS建立有限元模型，主梁以及主墩采用空间梁单元beam188，墩连接板处采用空间板单元shell63，建立桥的有限元模型，如图2所示.其中从左到右墩号依次为6#、7#、8#和9#.

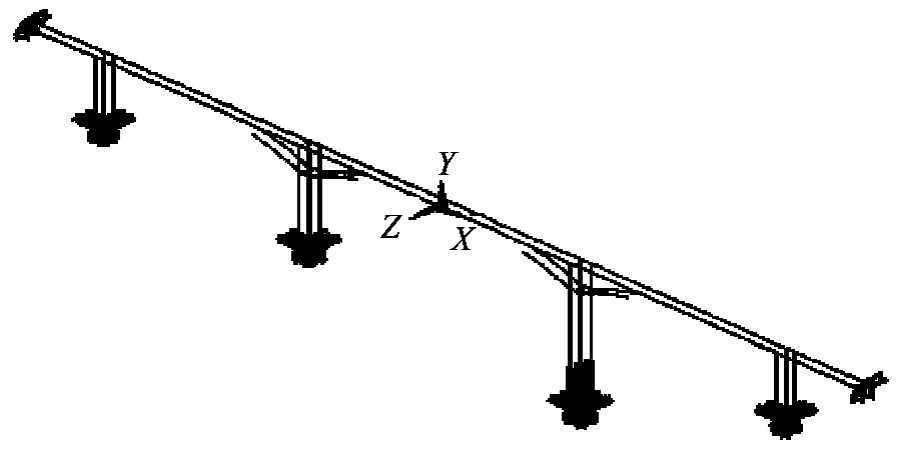
图2 北盘江大桥有限元摸型Fig.2 The finite element model of Beipanjiang bridge

2.2 结构动力特性和地震波的选取

对北盘江大桥进行动力特性分析，时程分析采用纽马克算法，计算桥的顺桥向地震响应分别采用加速度输入、LMM和LSM，验证它们在一致激励情况下的一致性和可靠性.

采用LMM时，用mass21单元模拟大质量，取大质量为结构总质量的108倍及更大时，计算结果趋于稳定，因此本算例中取大质量为结构总质量的108倍.在6#、7#、8#和9#墩底处依据墩底节点生成质量单元，去掉顺桥向墩底相应的约束，在去掉约束的节点上施加动力Ps=M0，其中

g为实际地震动加速度记录，α和β按照前文所述计算.

利用LSM时，采用combin14单元对原结构进行改造，去掉6#、7#、8#和9#墩顺桥向的相应约束，将墩底节点在顺桥向复制，用弹簧单元连接，为保证结构的动力特性不改变，取弹簧刚度为1.0×1013N·m－1.在原节点顺桥向施加Ps=KssXg的动力，其中Xg为地震加速度记录积分得到的位移时程.采用改进的LSM时，仅结合公式(15)对输入位移进行修正.

基于上述所述，采用加速度输入、LSM及改进的LSM时，桥的前两阶振型分别为横桥向同向侧弯和顺桥向同向侧弯，周期分别为6.13和4.93 s;采用LMM时，前16阶均为桥的刚体位移，第17和18阶周期分别为6.13和4.93 s，其余周期同加速度输入.

选取地震波时，根据《公路桥梁抗震设计细则》5.3.2条中规定:为考虑地震动的随机性，加速度时程不得少于三组，且应保证任意两组间同方向时程由下式定义的相关系数ρ的绝对值小于0.1.

依据上述原则，选取了Imp.Vall(1979，El Centro ARRAY#13)波、Loma Pr(1989，Agnews State Hospital)波和Imp.Vall(1979，Brawley Airport)波，位移时程由加速度时程积分得到［7］.

2.3 结果与分析

在三组地震作用下，以8#墩和主梁主要控制截面的地震响应为代表，结果见图3～图5，表1～表2.

通过图3～图5、表1和表2数据对比分析可知，无论桥墩还是主梁，LMM可以提供与加速度一致激励几乎完全一致的结果，最大内力误差在10－5，与理论分析式(10)相符;LSM与加速度一致激励相比，存在一定的误差，由表1知，6#、7#和9#墩，采用LSM时最大误差在27.8%，利用式(15)对其进行改进后，最大误差在17.3%，有较好的效果;图5和表2表明梁上位移及剪力等误差均较小，剪力最大误差为7.9%;而对于8#墩来说，由图3和表1可看出，墩在接近基底处误差较大，最大误差达到49.1%，利用公式(15)对LSM进行修正，由图3和表1可知采用改进方法有一定的效果，但对不同的地震波，采用改进方法后结构底部误差效果不同;基于上述分析，对于复杂的结构体系，与加速度直接输入相比较，采用LMM计算一致激励具有较好的一致性和稳定性，而LSM以及改进的LSM的应用受到一定的限制，需要进一步的分析研究.

图3 三条波作用下墩8－a剪力图Fig.3 Shear force diagram of the 8 － a pier under the action of three waves

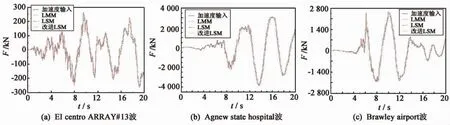
图4 三条波作用下墩8－a墩顶剪力时程图Fig.4 Shear force time diagram of the 8 － a pier top under the action of three waves

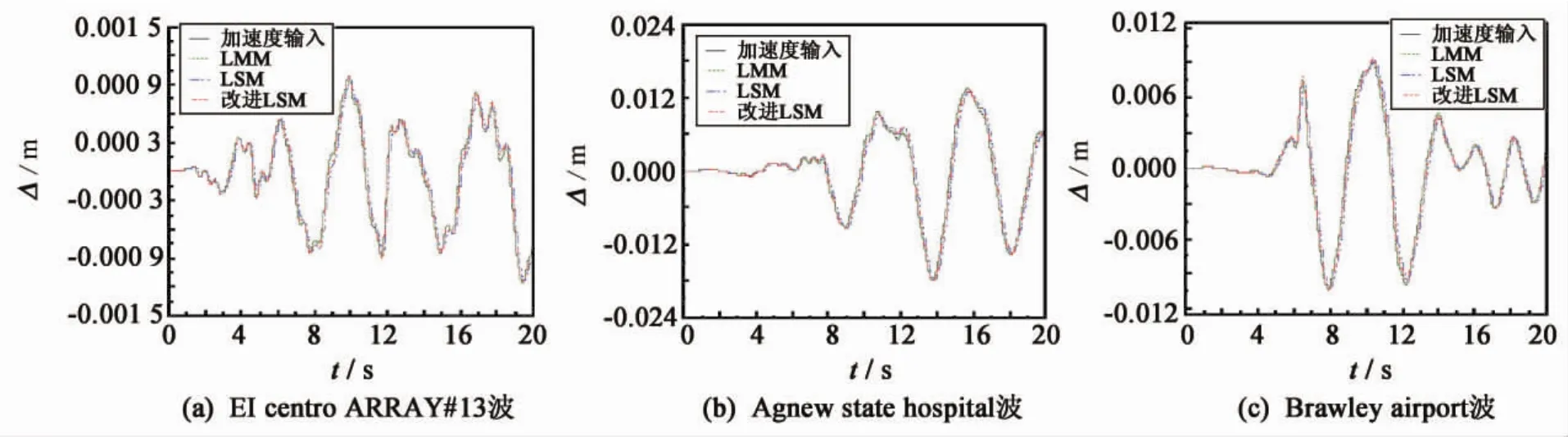
图5 三条波作用下梁跨中截面竖向位移图Fig.5 The vertical displacement diagram of the beam cross section under the action of three waves

表1 墩底弯矩比较Tab.1 The moment comparison of the pier bottom (kN·m)

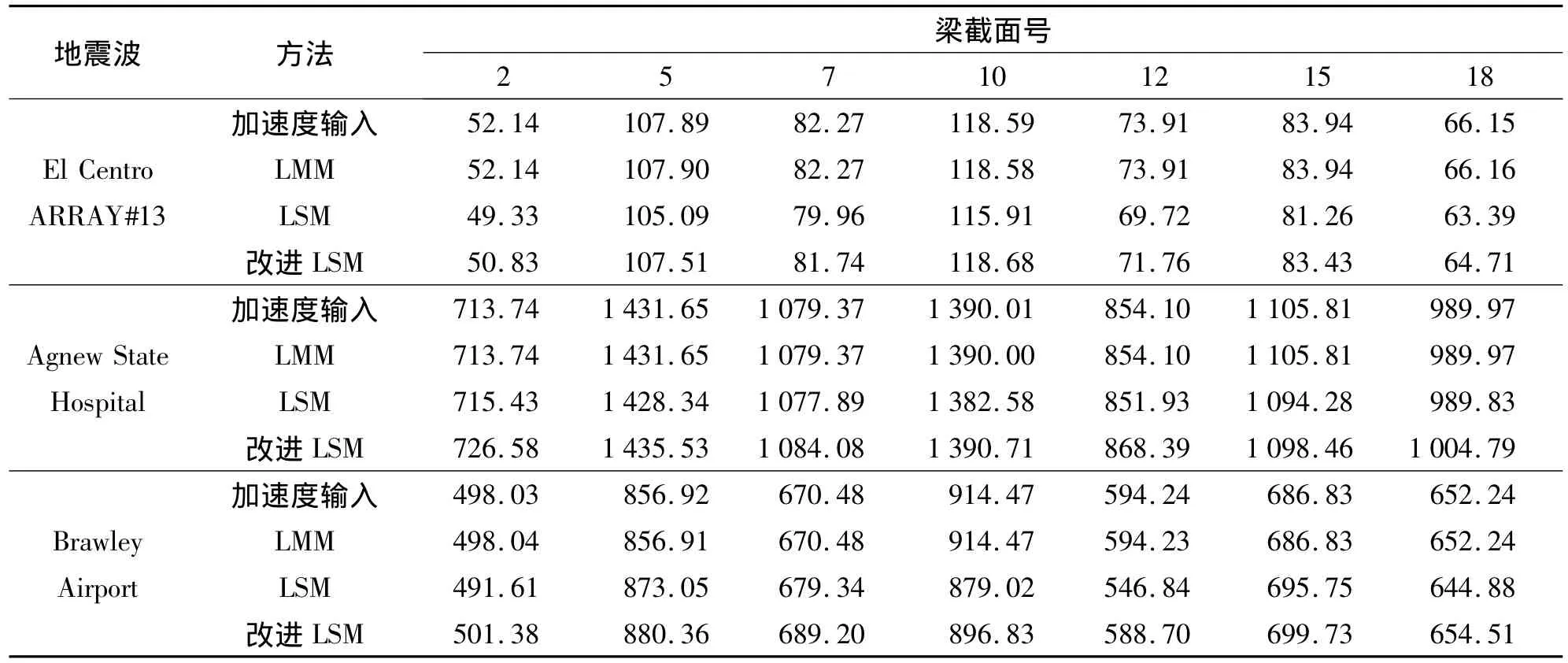
表2 梁截面剪力比较Tab.2 The shear comparison of the beam cross－section (kN)

3 结语

通过对地震激励计算方法的总结分析以及算例分析，可以得出如下结论:

1)一致激励时，LMM巧妙利用置大数的方法得到近似于真实值的地震动输入结果;与LSM相比较，具有较高的可靠性，从而为地震多点激励计算提供方向和参考;为分析地震多点激励，LMM应用上的误差主要来源和影响因素对大跨结构的效果，以及具体改进方法、结果可参考文献［4］等.

2)应用LSM一致激励近似计算时，会产生一定的误差，尤其是对结构底部剪力、弯矩的影响较大;误差分析表明，基于瑞利阻尼的一致激励分析中，质量阻尼系数和刚度阻尼系数都对其有影响，针对主要因素对LSM进行改进，改进后的LSM结果较改进前有一定的改善，具有一定的参考价值;另外，LSM用于多点激励分析时，误差产生的主要原因分析以及改进方法可参考文献［6］等.

3)LSM同直接位移输入法类似，受到位移时程的影响，位移时程的准确性影响到其精度，因此，需对位移时程的处理进行进一步的研究;除此之外，对于复杂的结构体系，利用LSM以及改进的LSM时，结构底部附近，无论是剪力还是弯矩均受到较大的影响，究其原因需要进一步的分析研究.

［1］柳国环，李宏男，林海.结构地震响应计算模型的比较与分析［J］.工程力学，2009，26(2):10－15.

［2］Wilson E L.Three－dimensional static and dynamic analysis of structures［M］.Berkley:Computer and Structures，2002.

［3］柯世堂，张令心，李永强.基于位移荷载输入动力时程分析法的误差分析［J］.山东理工大学学报，2009，23(5):5－8.

［4］周国良，李小军.用改进的大质量法分析行波效应对连续刚构桥地震反应的影响［J］.土木工程与环境工程，2010，32(2):217－220.

［5］王波，张海龙.基于大质量法的高墩大跨连续刚构桥地震时程反应分析［J］.桥梁建设，2006(5):17－20.

［6］周国良，李小军，刘必灯.大刚度法在结构动力分析中的应用、误差分析与改进［J］.工程力学，2011，28(8):30－36.

［7］Liao S，Zerva A.Physically compliant，conditionally simulated spatially variable seismic ground motions for performance－based design［J］.Earthquake Engineering and Structural Dynamics，2006，35:891 －919.

［8］陈文辉，罗永峰.地震激励输入方法对结构弹性响应的影响［C］//刘锡良.第九届全国现代结构工程学术研讨会.北京:工业建筑出版社，2009:439－448.