高强钢筋高强混凝土预应力梁短期刚度研究
叶献国,闫丽萍,种 迅,蒋 庆
(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;2.清华大学土木工程系,北京 100084;3.安徽土木工程结构与材料省级实验室,安徽合肥 230009)
0 引言
目前,国外学者对高强钢筋高强混凝土已有不少研究,并取得了一定成果[1-2],国内在这方面的研究大多限于单方面的预应力或高强钢筋或高强混凝土[3-5],对于同时采用高强钢筋和高强混凝土梁的试验研究仍很少.随着钢筋强度和混凝土强度的不断提高,构件截面尺寸相应减小,有可能发生结构的承载力满足要求而挠度变形不能满足正常使用要求的情况,使得刚度问题成为高强钢筋高强混凝土应用的瓶颈,而预应力技术的应用,可以改善结构的刚度[6],提高结构的变形性能.为研究双高预应力梁的受力性能,本课题组设计并制作了12根足尺高强钢筋高强混凝土预应力梁,对其进行了抗弯性能试验.本研究主要根据试验现象及试验数据分析梁的短期刚度影响因素,并验证中美混凝土规范刚度计算公式的适用性.
1 试验概况
1.1 试件设计
试验的主要目的是分析高强钢筋高强混凝土预应力梁的受弯性能,12根足尺试验梁均为后张有粘结预应力等截面矩形梁,尺寸为b×h×l=200 mm×450 mm×5 800 mm,混凝土强度等级为C80或C100,纵向受力非预应力筋采用HRBF500级钢筋,箍筋为HRB400级钢筋,预应力筋采用低松弛1 860级1×7股钢绞线.详细参数见表1.
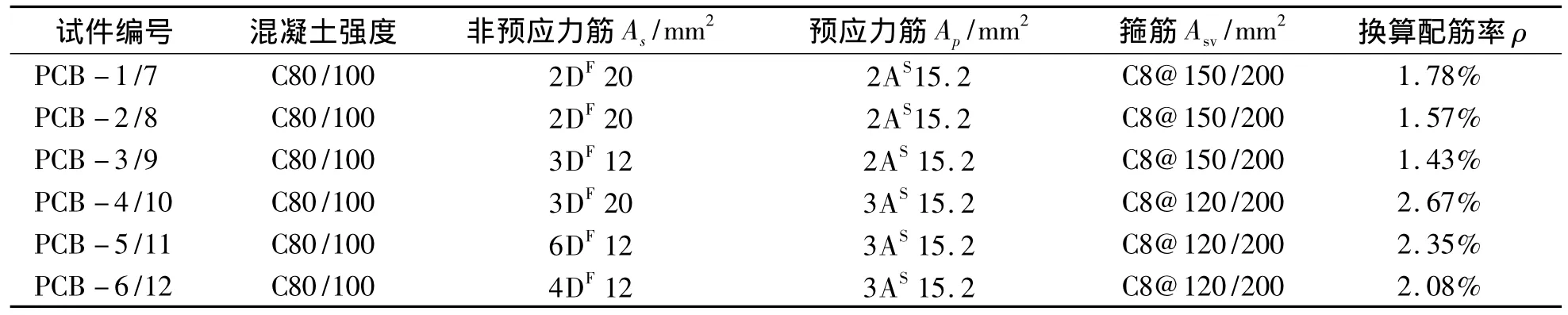
表1 试件参数Tab.1 Parameters of specimens
1.2 试件材料性能
1.2.1 混凝土力学性能
试验梁在浇筑的同时预留混凝土立方体标准试块(100 mm×100 mm×100 mm),分别在标准条件下和同条件下养护28 d后测量其抗压强度;棱柱体标准试块(150 mm×150 mm×300 mm),在标准条件下养护28 d后的抗压强度,见表2.

表2 混凝土材料抗压强度Tab.2 Compression strength of the concrete
1.2.2 钢筋性能试验
对试验所用钢筋按照《金属材料室温拉伸试验方法》进行了单轴受拉力学性能试验,测量不同直径的钢筋和钢绞线的屈服强度和极限强度,并计算伸长率.结果见表3.

表3 HRBF500MPa钢筋及钢绞线材料力学性能Tab.3 Mechanical properties of the HRBF500 reinforcing bars and the strands
1.3 加载及量测方案
试验梁简支,采用三分点对称集中加载,分两阶段控制,屈服前采用荷载控制,分4~5级加载;屈服后采用位移控制,按试件屈服时跨中挠度△y的倍数逐级加载,直至梁受弯承载力下降至极限承载力的85%左右时结束试验.试验正式加载之前进行预加载,正式加载过程中,每级荷载完成后持荷10 min观察变形及裂缝的发展状况,加载装置如图1所示.
在梁支座上方和跨中均布置位移计,测量支座变形及跨中挠度变化;在非预应力筋上布置规格为3 mm×2 mm电阻应变片,测量钢筋的应变;为防止混凝土局部压碎,在支座及加载处均设尺寸为200 mm×100 mm×25 mm的钢板.试验测点布置如图1所示.
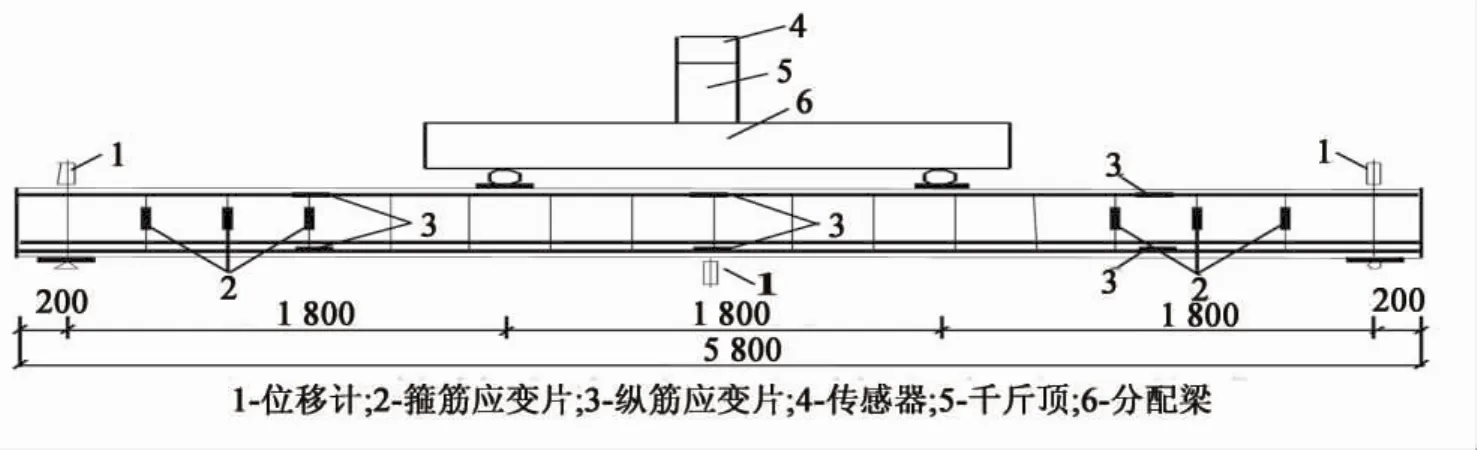
图1 试验加载装置及测点布置图(单位:mm)Fig.1 Test setup and arrangement of measuring device(unit:mm)
2 试验结果及分析
2.1 平截面假定的验证
试验过程中采用位移计测量了试验梁不同高度处各截面混凝土在300 mm标距内的平均应变,以PCB-7和PCB-10为例,平均应变沿截面高度分布情况如图2所示.可以看出,随着荷载的增加,梁截面中和轴逐渐地向上移动,混凝土的平均应变呈线性分布,基本符合平截面假定.

图2 PCB-7、PCB-10平均应变沿截面高度分布图Fig.2 The average strain distribution along the section height
2.2 梁跨中挠度分析
绘制了梁跨中弯矩-挠度曲线,以PCB-1、PCB-7、PCB-9为例,如图3.梁的受弯破坏过程表现出较为明显的4个阶段:第1阶段为弹性阶段,梁的变形随荷载的增加呈线性增长,抗弯刚度基本不变;第2阶段为弹塑性阶段,弯矩达到约(0.3~0.4)Mu时,出现第一个转折点,为梁的正截面开裂点,开裂导致梁的抗弯刚度退化为第1阶段的40%~65%,试验梁的变形随荷载的增加呈非线性增长,抗弯刚度因裂缝的产生和发展而逐渐降低;当弯矩达到(0.9~1.0)Mu时,出现第二个拐点,标志着梁进入第3阶段——塑性阶段,此后试验梁承受的荷载基本不变而变形不断增加,刚度逐渐退化为0;随着挠度的进一步增大,荷载开始退化,进入第4阶段——破坏阶段,此阶段荷载不断退化,直至退化至极限荷载的85%时,认为梁已经破坏.

图3 梁弯矩-挠度曲线Fig.3 Curves of the bending moment-deflection
陆春华等人对HRBF500级钢筋非预应力混凝土梁进行了抗弯试验研究[7-8],得出结论:当荷载达到(0.15~0.3)Mu时,混凝土开裂,刚度开始出现退化,当荷载达到(0.6~0.7)Mu时,受拉钢筋屈服.杜毛毛,苏小卒等人对HRBF500级钢筋后账有粘结预应力混凝土梁的抗弯性能展开了研究[9],得到混凝土的开裂荷载约为(0.25~0.4)Mu,屈服荷载接近Mu的结论.本试验中,荷载达到(0.3~0.4)Mu时,混凝土开裂,达到(0.9~1.0)Mu时,钢筋屈服,表明在受拉区配置预应力筋能够推迟开裂荷载,延缓梁刚度的退化,从而减小梁在使用荷载下的挠度变形.
2.3 抗弯刚度影响因素分析
试验设计了两个主要参数:换算配筋率和混凝土强度等级.为了分析两个参数对梁短期刚度的影响,分别绘制开裂前后相同荷载作用下两种因素对梁挠度的影响曲线(图4、图5),可以得出结论:换算配筋率是影响梁短期刚度的一个重要因素,换算配筋率越高挠度越小,即短期刚度越大,并且这种影响主要体现在开裂后.混凝土强度等级对梁的短期刚度也有一定的影响,开裂前,短期刚度随着混凝土强度等级的提高而增大,开裂后,影响很小.
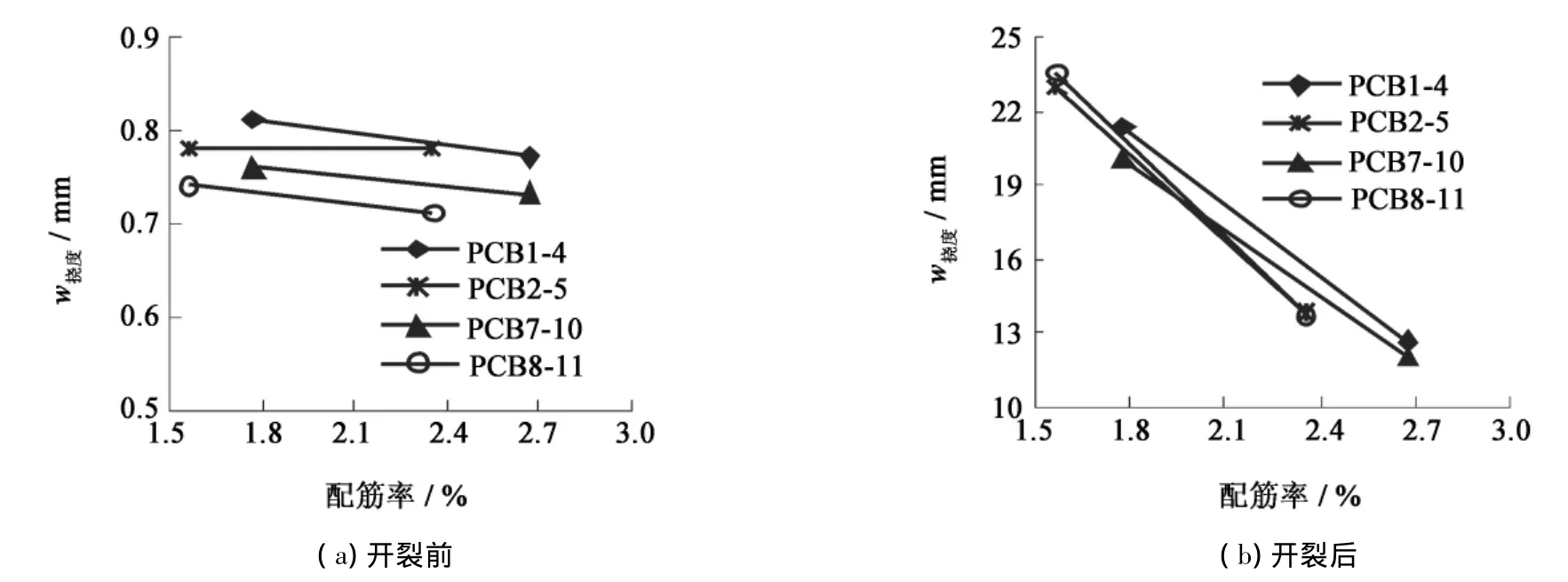
图4 换算配筋率对梁挠度的影响Fig.4 Influences of the conversion reinforcing ratio to stiffness

图5 混凝土强度等级对梁挠度的影响Fig.5 Influences of the concrete strength to stiffness
3 中美规范刚度计算结果对比分析
我国混凝土规范式[10]在计算梁短期刚度时,按裂缝控制等级要求,分别采用以下公式,式中具体参数见规范.
要求不出现裂缝的构件:
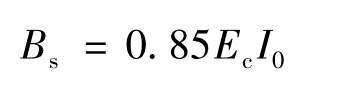
允许出现裂缝的构件:
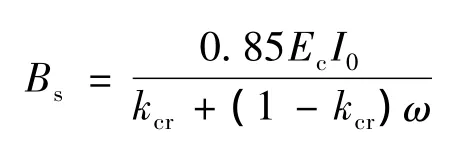
美国混凝土规范[11]刚度计算公式基于有效惯性矩理论,刚度计算公式为:
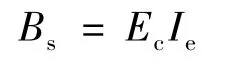
开裂前:
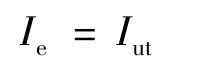
开裂后:
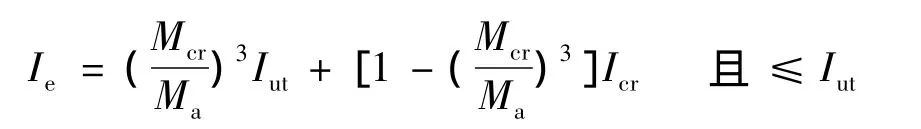
式中:Iut为未开裂换算截面惯性矩;Icr为开裂后不考虑拉区混凝土作用的换算截面惯性矩.
中美两种规范在计算构件挠度时,采用简化的分析方法,假定各同号弯矩区段内的刚度相等,并取用该区段内最大弯矩处的刚度,即最小刚度原理.因此,在满足平截面假定的基础上,可以根据结构力学的方法得出梁跨中挠度fm的计算公式:
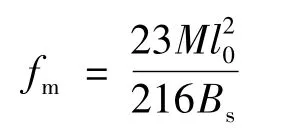
分别运用我国混凝土规范和美国混凝土规范中刚度的计算公式对12根梁的跨中挠度进行计算,将计算结果与试验结果对比,见表4,其中μ为试验值与计算值比值的平均值,δ为离散系数.
由表4可以看出:两种规范计算挠度值均大于试验值,说明两种规范都能更好的保证结构的刚度要求.开裂前,美国规范的计算结果比我国规范更接近试验值,原因是我国规范考虑了刚度折减系数0.85,而美国规范对刚度不进行折减;综合对比,开裂前后,μ均在0.8左右,δ基本在0.15左右,计算结果具有较高的精度,说明高强钢筋高强混凝土预应力梁的短期刚度可以按照中美两种规范进行计算.
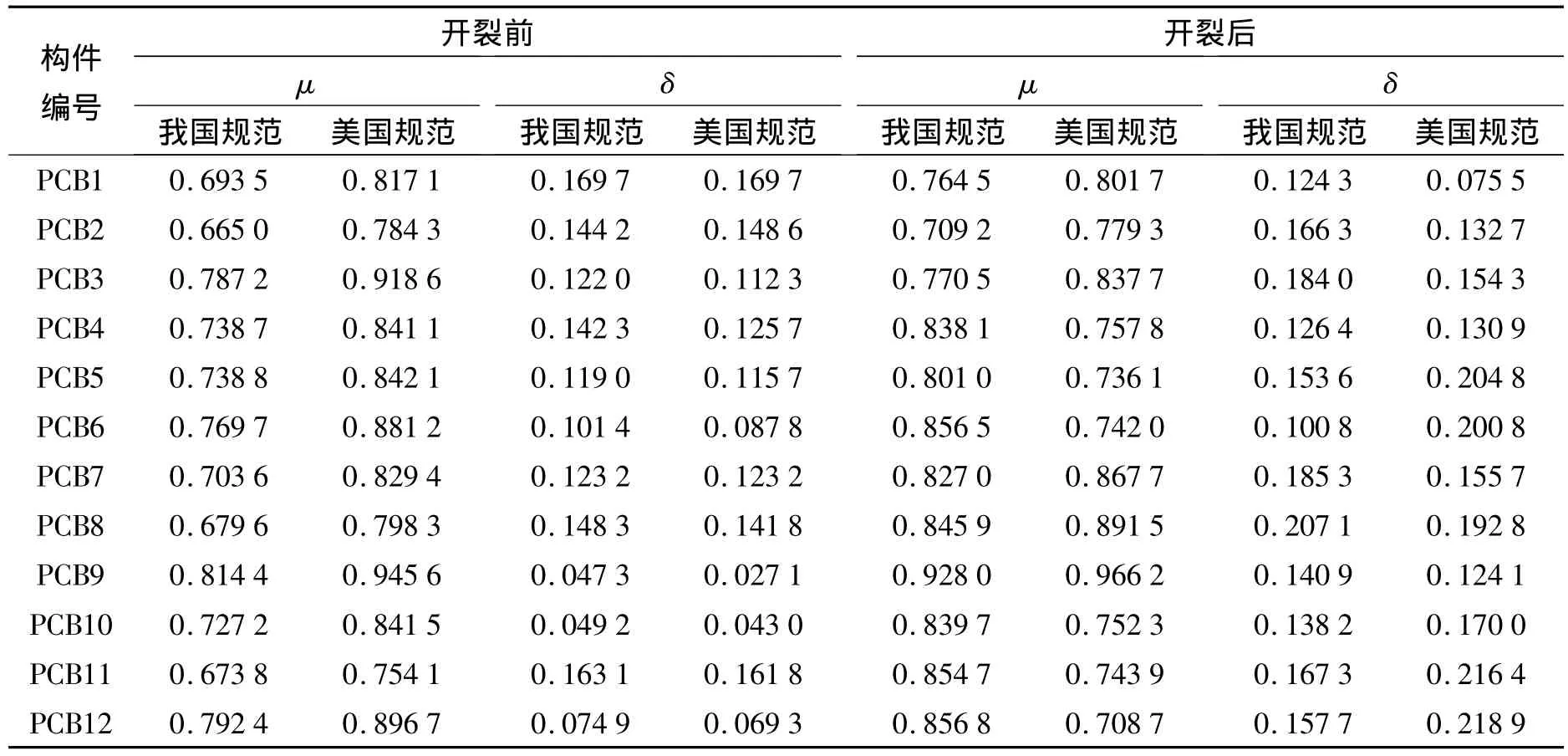
表4 挠度计算值与试验值对比Tab.4 Deflection comparison of calculated value and experimental value
4 结论
通过对12根足尺高强钢筋高强混凝土预应力梁进行抗弯性能试验,分析了梁抗弯刚度的影响参数及现有规范刚度计算公式的适用性,得到以下几个基本结论:
1)换算配筋率是影响梁短期刚度的一个重要因素,换算配筋率越高梁短期刚度越大,并且这种影响主要体现在混凝土开裂后.
2)混凝土强度等级对梁的短期刚度有一定的影响,但不明显,开裂前,短期刚度随着混凝土强度等级的提高而增大,开裂后,影响很小.
3)中美两国混凝土规范短期刚度计算结果与试验结果的对比表明,两种规范刚度计算公式对于高强钢筋高强混凝土预应力梁仍然适用.
[1]Hemdan S.Deflection prediction for FRP -strengthened concrete beams[J].Journal of Composites for Construction,2010,14:244-248.
[2]Mohammadhassani M,Jumaatat M Z B,Chemrouk M,et al.An experimental investigation on bending stiffness and neutral axis depth variation of over- reinforced high strength concrete beams[J].Nuclear Engineering and Design,2011,241(6):2060 -2 067.
[3]张耀庭,孙尧洲,张正哲.预应力钢筋混凝土梁挠度计算研究[J].华中科技大学学报:城市科学版,2006,23(4):27-30.
[4]黄伟,张丽,吴明超.HRB500级钢筋混凝土梁受弯性能试验研究[J].工业建筑,2011,41(7):58-61.
[5]梁书亭,蒋永生,陈德文.部分预应力高强混凝土梁正常使用极限状态验算方法研究[J].工业建筑,2001,31(2):56-59.
[6]Iskhakov I,Ribakov Y.From high strength and high performance concrete to high performance RC bending elements[J].High Performance Structures and Materials,2008:73 -82.
[7]陆春华,金伟良,延永东.正常使用状态下HRB500钢筋混凝土梁受弯性能试验[J].江苏大学学报:自然科学版,2011,32(3):350-354.
[8]谭赟.配500MPa级钢筋混凝土梁短期刚度计算模式试验研究[D].上海:同济大学,2009.
[9]杜毛毛,苏小卒,赵勇.配500MPa钢筋后张有粘结预应力混凝土梁受弯试验[J].沈阳建筑大学学报:自然科学版,2009,25(2):212-216.
[10]中华人民共和国住房和城乡建设部.GB 50010-2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
[11]American Concrete Institute.Building code requirements for structual concrete(ACI 318 -08)and commentary[M].[s.l]:American Concerte Institute,2008.

