钢筋混凝土结构建筑群震害快速预测方法

吴兆旗，姜绍飞，林冬勇，艾武福

(福州大学土木工程学院，福建福州350116)

地震造成建筑物的倒塌或严重损坏是造成人员伤亡和经济损失的主要原因，因此，建筑物震害预测能为制定城市长期的抗震防灾规划和震后应急救援提供科学依据.传统的震害预测方法包括经验总结法、直接统计法、专家评估法等，在对建筑物震害预测时需要按照一定比例抽样，对抽样建筑物按照单体计算进行分析，依据统计得到建筑物易损性矩阵，进一步得到城市建筑群体的评价结果.对于城市一般建筑物抽样比例为该类建筑面的8% ～11%为宜［1］.对于大中城市来说势必耗费大量人力、物力，前期现场调查工作费时，也给后期数据提炼与计算带来困难.另外，群体易损性多数针对历史震害资料统计得到，预测结果与现场调查得到的经济损失结果存在较大差异.

基于上述问题，有专家提出了利用类比预测方法对建筑物的震害进行预测，并用在砌体结构建筑震害预测工作中［2－4］，该方法是通过已有建筑物单体的震害结果预测其他类似建筑物的震害.本研究基于模糊相似原理和熵权法确定权重，建立了钢筋混凝土结构震害类比预测方法.

1 抗震性能评估指标

钢筋混凝土框架结构的破坏主要是由梁和柱构件破坏、节点破坏、填充墙破坏以及梁柱构件与填充墙墙之间的连接破坏引起.大量试验研究结果表明，层间位移角能够较好的反映框架结构各楼层间梁、柱、填充墙变形和层高的影响，而且与结构破坏状态有较好的相关性［5］.因此，层间位移角作为钢筋混凝土框架结构的抗震性能评估指标是合适的，这也与我国《建筑抗震设计规范》(GB 5011－2010)所选取的层间位移角作为抗震性能指标相一致.

目前，已有许多研究人员提出了以层间位移角为参考值的抗震性能性能量化指标.例如，西安建筑科技大学门进杰等人［6］和杨君［7］提出了框架结构抗震性能量化指标;刘景良［8］根据国内外已有试验结果，综合统计分析得到钢筋混凝土框架结构和带填充墙钢筋混凝土框架结构的层间位移角.本文选取文献［8］中的层间位移角(如表1所示)作为钢筋混凝土框架震害预测的评估指标.

表1 框架结构性能水准与层间位移角限值Tab.1 performance levels and inter－story displacement angle of frame stractures

2 震害预测方法

以动力时程分析对所选取的典型混凝土框架结构进行分析，并结合熵权法与模糊数学理论中的欧氏距离，提出了一种快速且精度较高的的群体钢筋混凝土框架结构震害类比预测方法.首先选择具有地区代表性的单体结构作为典型结构.考虑到所研究地区钢筋混凝土框架结构的特点及抗震设防等级，选取使用用途、层数、建设年代、设防烈度及场地类别等不同的框架结构，采用SAP2000对其进行动力时程分析，得到这些结构薄弱层的层间位移角精确计算结果，其他待预测结构的震害结果是通过与典型单体进行类比分析得到，即根据典型与待预测混凝土框架结构的各影响因子的异同，分别选取它们所对应的属性值，再通过相似度计算公式得到两者的相似度，与典型结构的精确计算结果进行类比，得到待预测结构的震害结果，最后将所有结果统计分析，得到所研究地区钢筋混凝土框架结构群体的震害预测结果.

2.1 抗震性能影响因子属性值的确定

选取不同典型混凝土框架结构进行抗震性能分析，确定不同使用用途、层数、场地类别、设防烈度及建设年代对混凝土框架结构的影响.然后将分析获得的层间位移角按照各影响因子进行分类、统计得到各影响因子的属性值如表2所示.

2.2 影响因子权重的确定

采用熵权法［2，9］确定各影响因子的权重值.

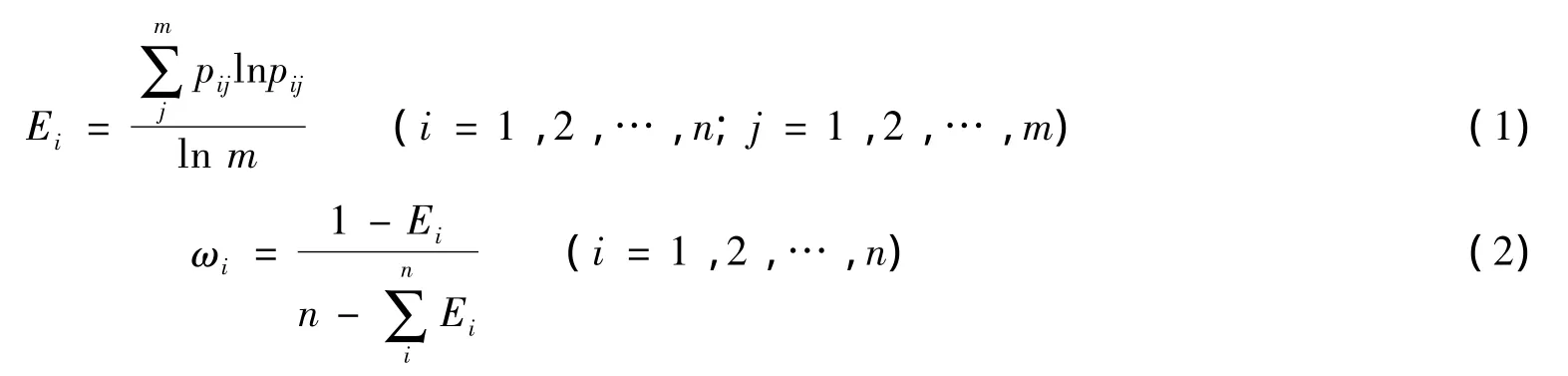
其中:pij为属性值;ωi为权重值;Ei为影响因子的信息熵.由式(2)可以得到6个影响因素的权重值，如表2所示.可以看出，选用的五个影响因子对抗震性能权重的大小排列顺序为:设防烈度＞房屋层数＞场地类别＞建设年代＞用途，与使用灰色关联度分析的5个主要影响因子的排列顺序地震烈度＞房屋层数＞地质条件(场地类别)＞建设年代＞使用用途的排列结果及各影响因子对抗震性能的影响程度大小均相差不大，说明通过震害实例分析得到的各影响因子对混凝土框架结构抗震性能的影响程度大小和本文所提出的理论方法分析得出的结果能够较好的吻合，因此本文所选取的理论分析方法具有一定的可信度.

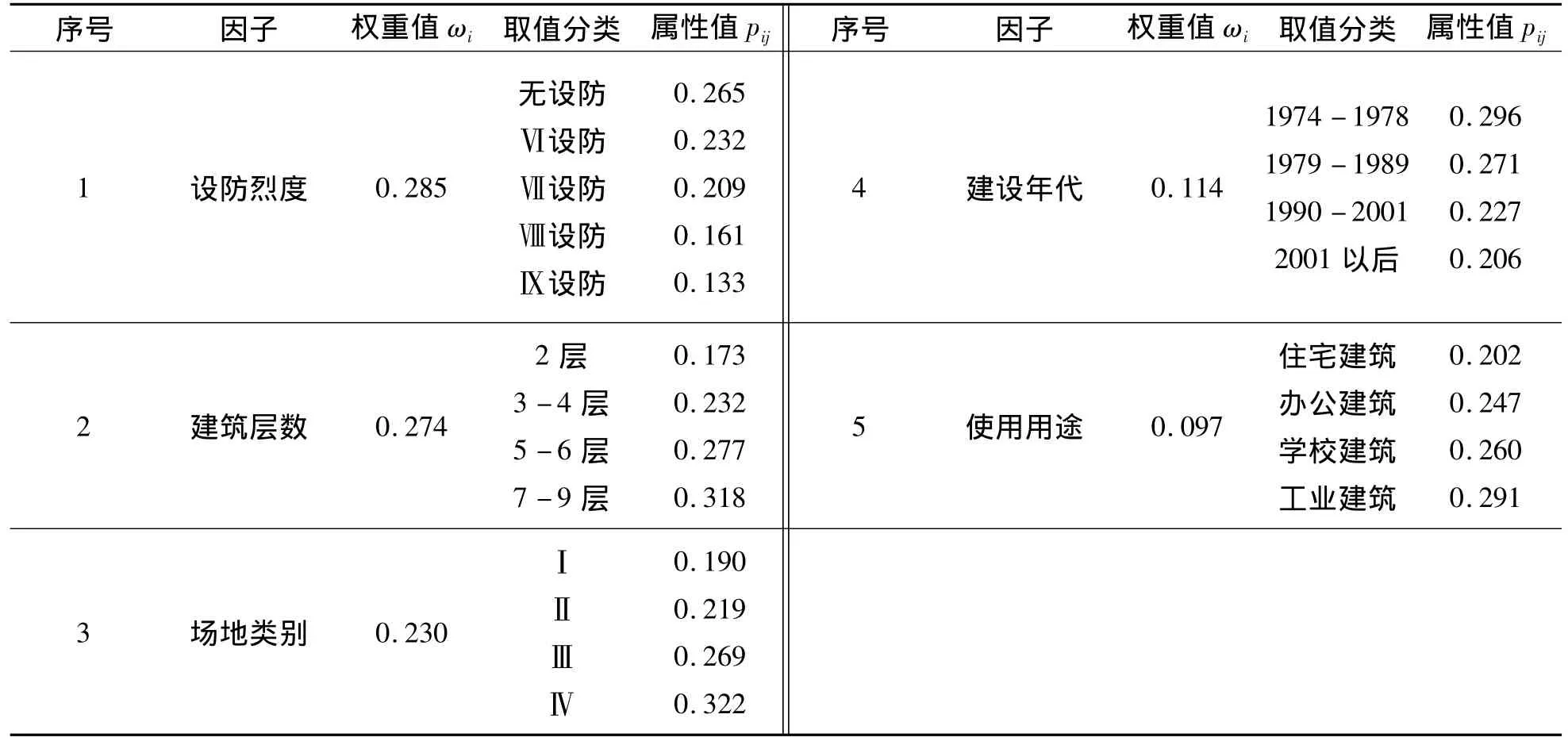
表2 抗震性能影响因子权重及分类取值表Tab.2 Determination of seismic influence factors and their weights

2.3 相似度的计算

在综合相似度的计算中，通常采用模糊数学中函数来对已知单体与未知单体的抗震能力进行比较.根据匹配函数和欧氏距离［10］，提出的新的相似度加权计算公式，即:

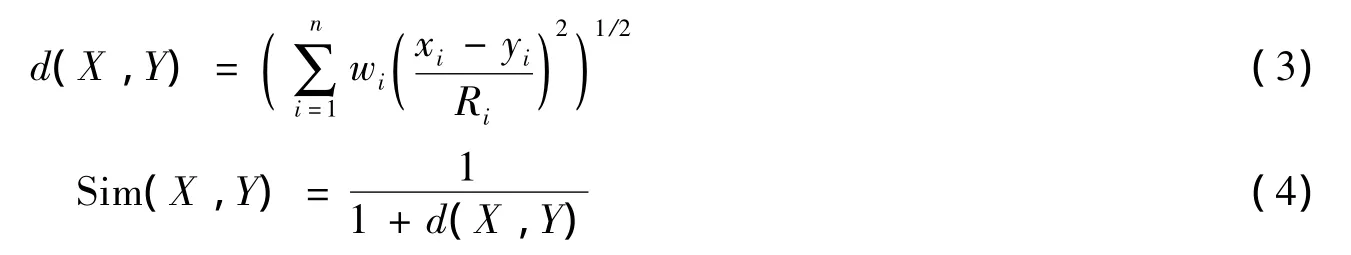
式中:Sim(X，Y)为已知单体与未知单体的相似度;Wi为影响因子权重;n为属性个数;xi、yi为第i个影响因子的各属性取值;Ri为第i个影响因子属性值的取值范围;d(X，Y)为欧氏距离.式(3)、(4)主要是为了计算建筑物之间的相似度，通过类比分析，得到所要预测建筑物的预测结果.

3 震害预测方法的应用

3.1 结构单体震害预测

选择一栋典型建筑和一栋待测建筑，分别进行静力弹塑性分析和动力时程分析，得到典型和待预测建筑结构薄弱层的层间位移角.应用本文方法预测待测建筑的震害，并与有限元结果进行比较，验证预测方法的有效性.

3.1.1 建筑物基本情况

典型建筑:福州毛纺厂精纺车间，层数为4层，层高均为5.2 m，建于1982年.场地类型Ⅲ类，设计分组第一组，七度设防(0.1g)，柱截面尺寸为400 mm×500 mm，主梁的截面尺寸为250 mm×600 mm，次梁为200 mm×450 mm，梁和柱均采用C25混凝土.箍筋采用一级钢，受力钢筋采用二级钢，结构平面布置如图1所示.

待测建筑:5层轻工厂房生产综合楼［12］，1～4层的层高为5.0 m，5层为3.6 m，建于2001年以后，II类场地，设计分组第二组，VIII度设防，中柱一二层为700 mm×700 mm，其它层柱截面为600 mm×600 mm，边柱截面均为600 mm×600 mm，梁截面为400 mm×800 mm，纵向钢筋HRB400，箍筋HRB335，柱混凝土强度等级一层为C30，其它层为C25，梁强度等级C25.结构平面布置如图2所示.

图1 典型建筑结构平面图(单位:mm)Fig.1 Structural plan of typical building(unit:mm)

图2 待测建筑结构平面图(单位:mm)Fig.2 Stractural plan of building to be predicted(unit:mm)

3.1.2 分析及预测结果

根据GB50011－2009要求取3条地震作用记录进行弹塑性时程分析，并取计算结果平均值作为精确结果.有限元分析得到的预测建筑和待测建筑薄弱层的层间位移值列于表3.用公式(3)、(4)得到待测建筑与典型建筑之间的相似度为:Sim(X，Y)=0.893.根据本文预测方法得到待测建筑的薄弱层层间位移角和相应的破坏特征也一并列于表3.从表3可以看出，预测结果与分析结果相差不大(6.0%以内);预测破坏状态和分析得到的破坏状态一致，满足实际工程的精度要求.

表3 单体结构震害预测与分析结果比较Tab.3 Compare of seismic damage prediction and analysis resutts of single RC frame structure

3.2 结构群体震害预测

选取26栋福州市的钢筋混凝土框架结构作为研究对象，用以验证所提震害预测方法的可靠性.其中5栋作为典型建筑，其余21栋作为待测建筑.选取典型混凝土框架结构的时候均考虑了建设年代、设防烈度、层数及使用用途等影响因子的不同，详细情况参见表4.

表4 典型钢筋混凝土框架结构详细情况Tab.4 Detailed information of typical RC frame structures

按照相似度公式计算得到五个相似度值，从中选取三个相似度最大的值，将其对应的框架结构层间位移角进行平均，从而减少震害预测结果的不确定性.待测建筑基本情况及相应的震害分析和预测结果见表5.从表5可以发现，用本预测得到的结果与有限元分析精确计算值结果相差不大，其中有4栋混凝土框架结构有限元分析出来的精确结果与类比预测结果的误差率超过了10%，但均在15%左右，其他的17栋建筑误差均小于10%.总体上来看预测结果具有一定的准确性且预测速度较快.此外21栋混凝土框架结构的预测震害与有限元分析精确计算的震害情况完全相符，预测结果较为精确且预测速度较快，满足实际工程的要求.

之所以会出现了一定的误差和选用的典型建筑密切相关.如在实际应用的过程中，选取更多与待预测混凝土框架结构相似度大的典型混凝土框架结构对每栋待预测混凝土框架结构进行震害预测，则这些误差可以减小甚至消除.

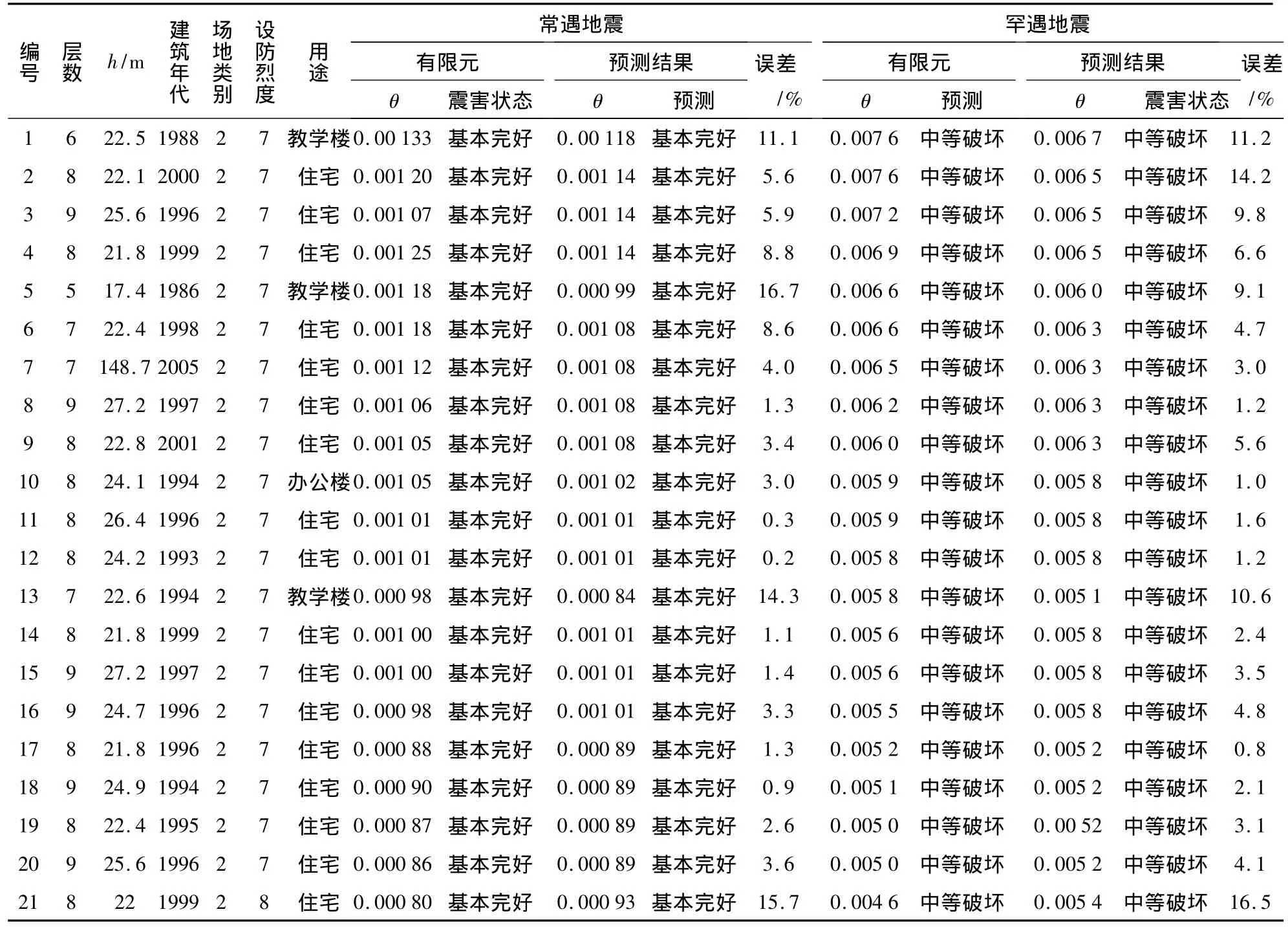
表5 待测混凝土框架结构建筑基本情况及震害预测结果Tab.5 Basic information and seismic damage prediction results of some RC frame structures

［1］冯启民.GB/T 19428－2003 地震灾害预测及信息管理系统技术规范［S］.北京:中国标准出版社，2003.

［2］姜绍飞，艾武福，李宁，等.群体砌体建筑的易损性分析及震害预测［J］.福州大学学报:自然科学版，2011，30(3):738－753.

［3］陈建云，毕可为，温瑞智.一种适于震后快速评估的群体易损性分析方法［J］.震害防御技术，2009，4(2):178－181.

［4］王志涛，苏经宇，马东辉，等.群体建筑震害特征类比预测方法及应用［J］.北京工业大学学报，2008，34(8):842－847.

［5］闫熙臣，高小旺.钢筋混凝土框架结构抗震评估的新方法［J］.工程抗震与加固改造，2007，29(1):103－105.

［6］门进杰，史庆轩，周琦.框架结构基于性能的抗震设防目标和性能指标的量化［J］.土木工程学报，2008，41(9):76－82.

［7］杨君.钢筋混凝土框架结构基于位移的抗震设计理论和方法［D］.西安:西安建筑科技大学，2007.

［8］刘景良.考虑填充墙影响的既有框架结构抗震性能评估［D］.福州:福州大学，2011.

［9］王茜，王雁凌，张粒子.影响电力需求预测各因子的客观权重分配方法［J］.电网技术，2008，32(5):83－86.

［10］谢全敏.滑坡灾害评价及其治理优化决策新方法［M］.武汉:武汉理工大学出版社，2008:94－107.

［11］混凝士结构设计规范算例编委会.混凝土结构设计规范算例［M］.北京:中国建筑工业出版社，2003.